Гордин Р.К. Геометрия. Планиметрия. 7-9 классы
Подождите немного. Документ загружается.


§ 2.7 301
A B
C
D
Рис. 383
M
1
A
A
1
A
2
B
B
1
B
2
M
M
2
Рис. 384
Тогда
CD
2
=
AD
AB
2
·CB
2
+
BD
AB
2
·CA
2
+
AD
AB
·
BD
AB
·(CB
2
+CA
2
−AB
2
),
или
AB
2
·CD
2
= AD
2
·CB
2
+BD
2
·CA
2
+AD·BD·(CB
2
+CA
2
−AB
2
)=
= (AD
2
+AD·BD)·CB
2
+(BD
2
+AD·BD)·CA
2
−AD·BD·AB
2
=
= AD·(AD+BD)·CB
2
+BD·(BD+AD)·CA
2
−AD·BD·AB
2
=
= AD ·AB · CB
2
+ BD · AB · CA
2
− AD · BD ·AB
2
.
Следовательно,
AB · CD
2
= AD · CB
2
+ BD ·CA
2
− AD · BD · AB.
2.449. Обозначим
# »
OA
1
+ . . . +
# »
OA
n
=
#»
a . При повороте на
угол
360
◦
n
вокруг точки O точка A
i
переходит в точку A
i+1
(1 6 i 6 n −1), а точка A
n
— в точку A
1
. Поэтому вектор
#»
a при
таком повороте переходит сам в себя. Следовательно,
#»
a =
#»
0 .
Далее,
# »
XA
1
+. . .+
# »
XA
n
= (
# »
XO+
# »
OA
1
)+(
# »
XO+
# »
OA
2
)+. . .+(
# »
XO+
# »
OA
n
) =
= n
# »
XO +
#»
0 = n
# »
XO.
2.450. Прямую.
Пусть A и B — точки, в которых находи-
лись пешеходы в начале движения (рис. 384). Через некоторое
время они оказались в точках A
1
и B
1
соответственно. Если M
и M
1
— середины отрезков AB и A
1
B
1
, то
# »
MM
1
=
1
2
(
# »
AA
1
+
# »
BB
1
).
Аналогично,
# »
MM
2
=
1
2
(
# »
AA
2
+
# »
BB
2
), где A
2
и B
2
— точки,
302 8 класс
O
1
O
2
O
3
O
4
A
B
C
D
M
N
Рис. 385
#»
e
1
#»
e
2
#»
e
3
A
B
C
Рис. 386
в которых находились пешеходы еще через некоторое время,
а M
2
— середина отрезка A
2
B
2
. Поскольку скорости пешеходов
постоянны, то
# »
AA
2
= k
# »
AA
1
и
# »
BB
2
= k
# »
BB
1
. Поэтому
# »
MM
2
=
1
2
(
# »
AA
2
+
# »
BB
2
) = k ·
1
2
(
# »
AA
1
+
# »
BB
1
) = k
# »
MM
1
.
Следовательно, точки M
1
и M
2
лежат на прямой, проходящей
через точку M .
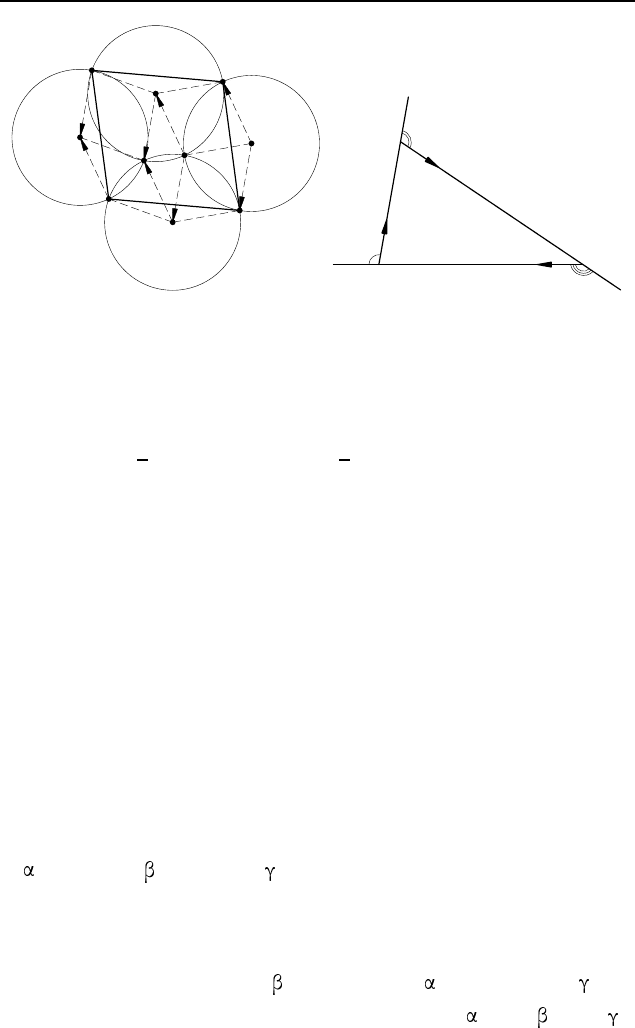
2.451. Пусть O
1
, O
2
, O
3
, O
4
— центры описанных окружно-
стей треугольников AMN, AMB, BMN, CN D соответственно
(рис. 385). Поскольку O
4
NO
3
C, N O
1
MO
3
, O
1
AO
2
M — ромбы,
то
# »
O
4
C =
# »
NO
3
=
# »
O
1
M =
# »
AO
2
. Поскольку O
4
DO
1
N, NO
1
MO
3
,
O
3
MO
2
B — ромбы, то
# »
O
4
D =
# »
NO
1
=
# »
O
3
M =
# »
BO
2
. Таким
образом,
# »
O
4
C =
# »
AO
2
,
# »
O
4
D =
# »
BO
2
. Следовательно,
# »
CD =
# »
O
4
D −
# »
O
4
C =
# »
BO
2
−
# »
AO
2
=
# »
BA,
т. е. ABCD — параллелограмм.
2.452. а) Отложим на сторонах AB, BC и CA треугольни-
ка ABC единичные векторы
#»
e
1
,
#»
e
2
и
#»
e
3
, сонаправленные век-
торам
# »
AB,
# »
BC и
# »
CA соответственно (рис. 386). Пусть ∠BAC =
=
, ∠ABC = , ∠ACB = . Тогда
0 6 (
#»
e
1
+
#»
e
2
+
#»
e
3
)
2
=
=
#»
e
2
1
+
#»
e
2
2
+
#»
e
2
3
+ 2 ·
#»
e
1
#»
e
2
+ 2 ·
#»
e
1
#»
e
3
+ 2 ·
#»
e
2
#»
e
3
=
= 1 + 1 + 1 + 2(cos(180
◦
−
) + cos(180
◦
− ) + cos(180
◦
− )) =
= 3 − 2(cos
+ cos + cos ).
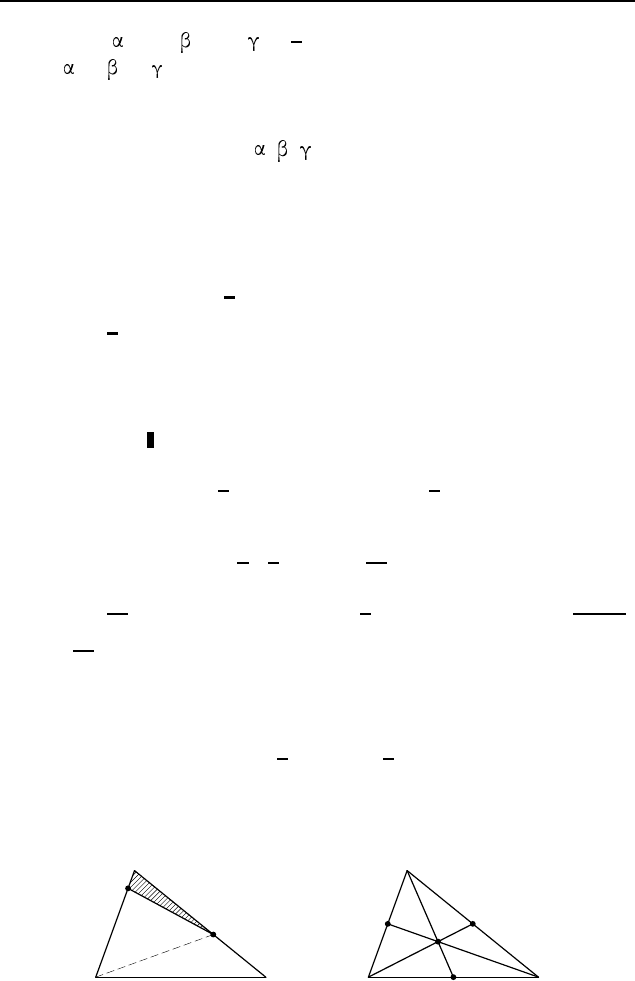
§ 2.8 303
Откуда cos + cos + cos 6
3
2
. Равенство достигается в случае,
когда
= = = 60
◦
, т. е. когда треугольник ABC равносто-
ронний.
б) Указание. Пусть O — центр описанной окружности тре-
угольника ABC с углами
, , . На радиусах OA, OB, OC отло-
жите единичные векторы
#»
e
1
,
#»
e
2
и
#»
e
3
. Тогда (
#»
e
1
+
#»
e
2
+
#»
e
3
)
2
> 0.
§ 2.8
2.453. 12. 2.454
0
.
1
4
.
2.460.
1
4
. Указание. Докажите, что четырехугольники
AMN D и BMNC — параллелограммы, и воспользуйтесь ре-
зультатом предыдущей задачи.
2.462. 14 и 21.
2.463
0
. 5.
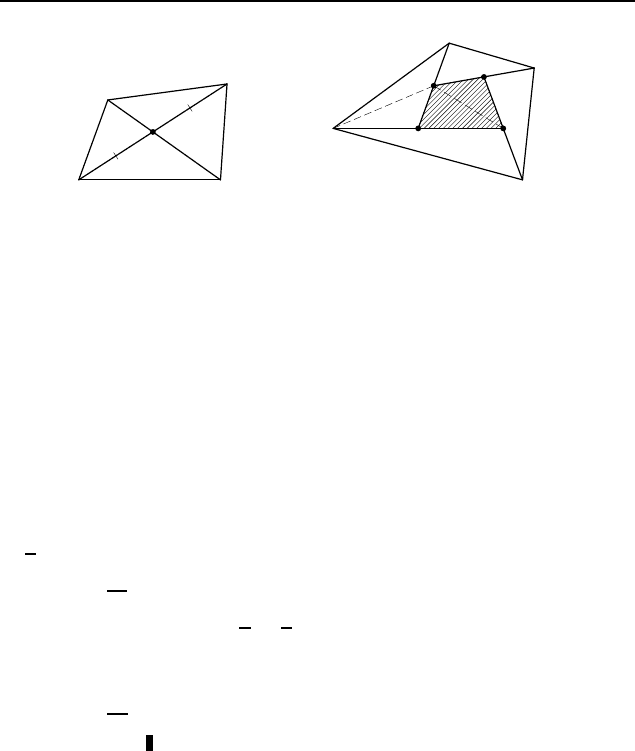
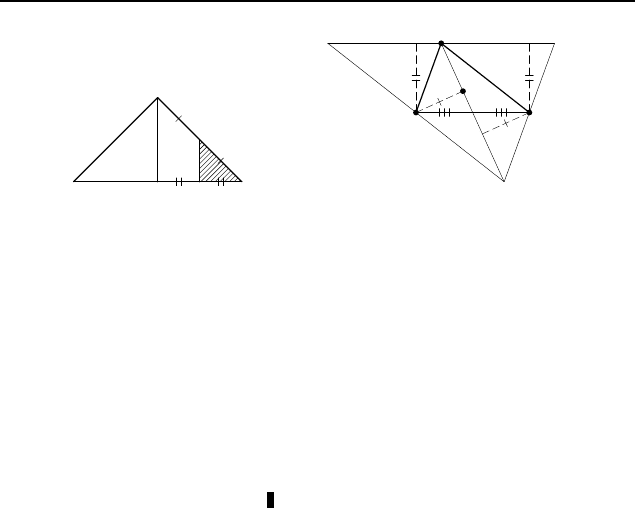
Соединим точки B и K (рис. 387). Тогда
S
ABK
=
3
5
S
ABC
, S
AMK
=
1
6
S
ABK
.
Поэтому
S
AMK
=
3
5
·
1
6
S
ABC
=
1
10
S
ABC
= 5.
2.464.
13
20
. 2.465. 9 : 5. 2.466.
1
4
. 2.468. 32. 2.469.
a
2
−b
2
4
.
2.470.
ab
2
. 2.471. 4.
2.472
0
. Пусть M — точка пересечения медиан AA
1
, BB
1
,
CC
1
треугольника ABC (рис. 388). Тогда
S
B
1
MC
=
1
3
S
B
1
BC
=
1
6
S
ABC
.
Аналогично для остальных пяти треугольников.
A
B C
K
M
Рис. 387
A
A
1
B
B
1
C
C
1
M
Рис. 388
304 8 класс
O
A
B
C
D
Рис. 389
A
A
1
B
B
1
C
C
1
D
D
1
Рис. 390
2.477. Пусть O — точка пересечения диагоналей AC и BD
четырехугольника ABCD (рис. 389). Если AO = OC, то
S
AOB
= S
COB
и S
AOD
= S
COD
.
Следовательно,
S
ABD
= S
AOB
+ S
AOD
= S
COB
+ S
COD
= S
CBD
.
2.478. Указание. Пусть M и N — соответственно середи-
ны сторон AB и BC данного четырехугольника ABCD. То-
гда MN — средняя линия треугольника ABC, поэтому S
MBN
=
=
1
4
S
ABC
.
2.479.
ab
4
. Указание. Искомый четырехугольник — прямо-
угольник со сторонами
a
2
и
b
2
.
2.480
0
. Указание. Соедините точки C и M и воспользуйтесь
результатом задачи 2.458
0
.
2.481.
7
16
.
2.482. 5s.
Заметим, что
S
ABD
+ S
ABC
+ S
BCD
+ S
ACD
= 2s
(рис. 390). Отрезок A
1
B — медиана треугольника AA
1
B
1
,
а BA — медиана треугольника A
1
BD, поэтому
S
AA
1
B
1
= 2S
AA
1
B
= 2S
ABD
.
Аналогично,
S
BB
1
C
1
= 2S
ABC
, S
CC
1
D
1
= 2S
BCD
,
S
DD
1
A
1
= 2S
ACD
.

§ 2.8 305
Следовательно,
S
A
1
B
1
C
1
D
1
=
= S
ABCD
+ S
AA
1
B
1
+ S
BB
1
C
1
+ S
CC
1
D
1
+ S
DD
1
A
1
=
= S
ABCD
+ 2S
ABD
+ 2S
ABC
+ 2S
BCD
+ 2S
ACD
=
= s + 4s = 5s.
2.483. Указание. Пусть точки M и N расположены соответ-
ственно на сторонах AB и AD параллелограмма ABCD, при-
чем AM : M B = AN : ND = 1 : 2 (рис. 391). Тогда прямые CM
и CN делят параллелограмм ABCD на три равновеликие части.
2.484. 14. Указание. Четырехугольник с вершинами в се-
рединах сторон данного четырехугольника — ромб (см. зада-
чу 2.478).
2.485. 48. Указание. Четырехугольник с вершинами в се-
рединах сторон данного четырехугольника — прямоугольник.
2.486. Указание. Отрезки, соединяющие точку внутри тре-
угольника с вершинами, разбивают треугольник на три тре-
угольника, сумма площадей которых равна площади данного
треугольника.
2.487. Указание. Отрезок, соединяющий точку на основа-
нии равнобедренного треугольника с вершиной, разбивает тре-
угольник на два треугольника, сумма площадей которых равна
площади данного треугольника.
2.488.
bc
a+b
,
ac
a+b
. Указание. S
ABM
= S
ACM
.
2.489
0
. Указание. Соедините центр вписанной окружности
с вершинами треугольника и сложите площади полученных тре-
угольников.
2.490. Указание. Пусть a и b — катеты прямоугольного тре-
угольника, c — гипотенуза, r — радиус вписанной окружности.
Тогда r =
a+b−c
2
.
2.491. Пусть S — площадь прямоугольного треугольника,
r — радиус его вписанной окружности, a и b — указанные от-
резки гипотенузы. Тогда
S = (a + b + r)r = ar + br + r
2
= (a + r)(b + r) − ab = 2S − ab,
откуда S = ab.
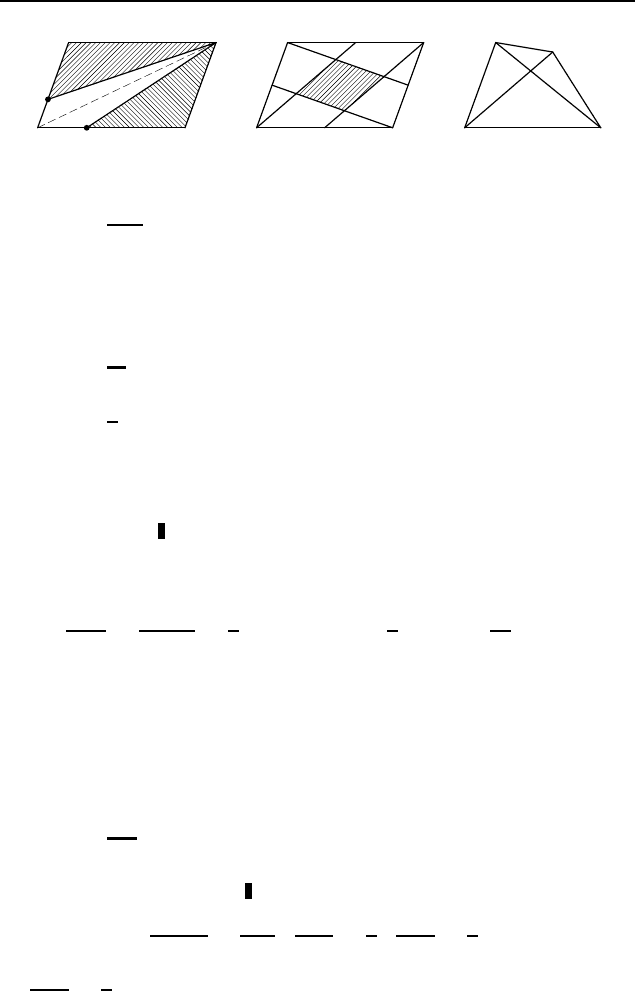
306 8 класс
A
B C
D
M
N
Рис. 391
E
H
A
B C
D
F
G
K
L
M
N
Рис. 392
M
A
BC
D
Рис. 393
2.492.
ab
a+b
. Указание. Соедините центр окружности с вер-
шиной прямого у гла и сложите площади полученных треуголь-
ников.
2.493
0
. Указание. Соедините центр окружности с вершина-
ми треугольника.
2.494.
c
2
8
. Указание. Проведите высоту и медиану из верши-
ны прямого угла данного треугольника.
2.495.
1
5
. Указание. Пусть прямая BM пересекает отрез-
ки AL и CN (рис. 392) соответственно в точках E и F , а пря-
мая DK — соответственно в точках G и H. Тогда EF HG —
параллелограмм, BE = EF = GH = DH = 2F M.
2.496. 120.
Пусть M — точка пересечения диагоналей AC
и BD четырехугольника ABCD (рис. 393). Если S
AMD
= 30,
S
AMB
= 10, S
CMD
= 20, то
BM
MD
=
S
AM B
S
AM D
=
1
3
и S
BMC
=
1
3
S
CMD
=
20
3
< 10.
Разбирая остальные возможные случаи, убеждаемся, что воз-
можны только два из них: S
AMB
= 20, S
AMD
= 10, S
CMD
= 30
или S
AMB
= 30, S
AMD
= 10, S
CMD
= 20. В каждом из возмож-
ных случаев S
BMC
= 60. Следовательно,
S
ABCD
= 10 + 20 + 30 + 60 = 120.
2.497.
3ab
4
. Указание. Через вершину C проведите прямую,
параллельную AB.
2.498. 45
◦
, 90
◦
, 45
◦
.
Поскольку
S
N M C
S
ABC
=
CN
BC
·
CM
AC
=
1
2
·
CM
AC
=
1
8
,
то
CM
AC
=
1
4
. Пусть BK — высота треугольника ABC (рис. 394).
Тогда NM — средняя линия треугольника BKC. Поэтому
§ 2.8 307
A
B
CK M
N
Рис. 394
M
1
A
B
C
M
2
M
3
M
4
Рис. 395
KM = MC и AK = KC, т. е. треугольник ABC — равнобед-
ренный. Следовательно, ∠C = 45
◦
, ∠B = 90
◦
.
2.499. Может.
2.500. а) Две параллельные прямые.
б) Прямая, содержащая медиану, проведенную к стороне BC,
и прямая, проходящая через вершину A параллельно BC.
в) Точка пересечения медиан треугольника ABC и вершины
треугольника, для которого стороны треугольника ABC явля-
ются средними линиями.
Из равенства площадей треуголь-
ников ABM и ACM следует, что точки B и C равноудалены
от прямой AM . Поэтому прямая AM параллельна BC или про-
ходит через середину стороны BC (рис. 395). Следовательно,
искомые точки — это точка пересечения медиан треугольни-
ка ABC и точки пересечения прямых, проходящих через верши-
ны треугольника ABC параллельно противолежащим сторонам
(точки M
1
, M
2
, M
3
и M
4
на рисунке 395).
2.501. Указание. Проведите высоты треугольников KNL,
ABK, CML и примените теорему о средней линии трапеции
(рис. 396).
2.502. Указание. Воспользуйтесь результатом предыдущей
задачи.
2.503. 20, 10, 5, 15.
2.504. Пусть M и N — середины сторон AB и CD выпук-
лого четырехугольника ABCD (рис. 397), S
AMND
= S
BMNC
.
Поскольку треугольники AMN и BM N равновелики, то рав-
новелики и треугольники ADN и BN C. Поэтому высоты AA
1
и BB
1
этих треугольников равны. Следовательно, AB k CD.
2.505. На продолжении отрезка DP за точку P отложите
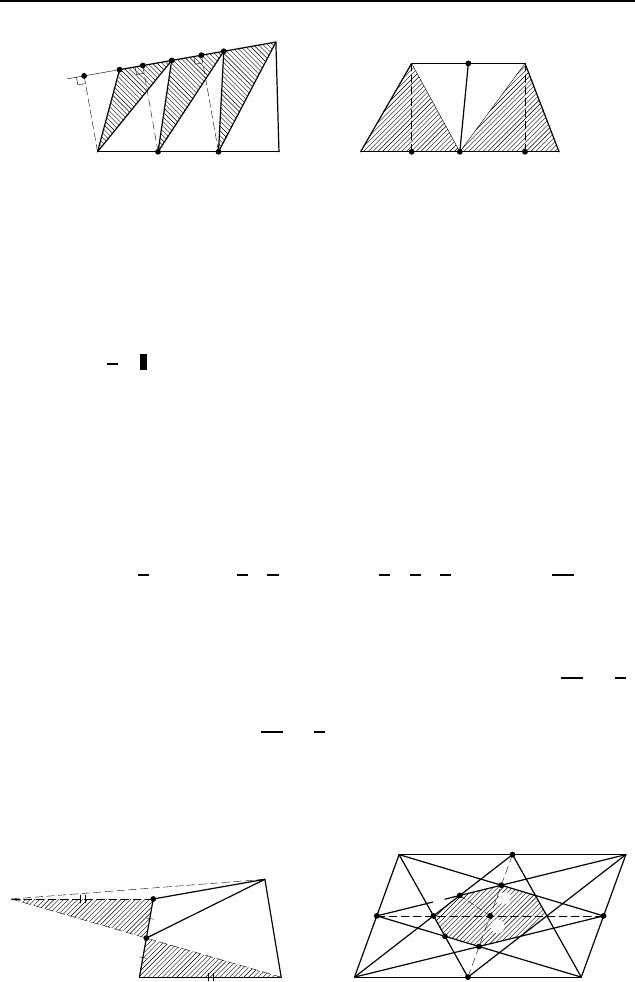
308 8 класс
A
A
1
B
C
D
K
L
M
M
1
N
N
1
Рис. 396
A
A
1
B
B
1
CD
M
N
Рис. 397
отрезок P D
1
= DP (рис. 398). Тогда треугольники D
1
P B
и DP A равны, поэтому S
D
1
P B
+ S
CP B
= S
DP A
+ S
CP B
=
= S
CP D
= S
D
1
P C
. Поэтому точка B лежит на отрезке D
1
C.
Поскольку D
1
B k AD, то BC k AD.
2.506.
1
6
.
Пусть точки K, L, M и N — соответственно
середины сторон AB, BC, CD и AD параллелограмма ABCD
(рис. 399). Тогда точка O пересечения KM и LN — центр па-
раллелограмма ABCD, точка E пересечения OL и KC — се-
редина OL, точка F пересечения AL и KO — середина KO,
поэтому KE и LF — медианы треугольника KOL. Если G —
точка их пересечения, то
S
OGE
=
1
6
S
KOL
=
1
6
·
1
2
S
OKBL
=
1
6
·
1
2
·
1
4
S
ABCD
=
1
48
.
Аналогично для остальных семи треугольников с вершинами в
точке O, из которых составлен рассматриваемый восьмиуголь-
ник. Следовательно, площадь восьмиугольника равна 8·
1
48
=
1
6
.
2.507. Указание. Разрежьте квадрат на 50 равных прямо-
угольников со сторонами
1
10
и
1
5
прямыми, параллельными его
сторонам. По крайней мере в один такой прямоугольник попа-
дут не менее трех из указанных точек.
B
A
C
D
D
1
P
Рис. 398
O
F
G
E
A
B C
D
K
L
M
N
Рис. 399

§ 2.8 309
2.508. Проведем через точку O
B
1
O
YA
B
C C
1
K
X
Рис. 400
прямую, отрезок BC которой, за-
ключенный внутри угла, делился бы
точкой O пополам (см. задачу 2.35).
Пусть B и C лежат на сторонах AX
и AY соответственно (рис. 400). Дока-
жем, что ABC — искомый треуголь-
ник. Проведем через точку O прямую,
пересекающую AX и AY в точках B
1
и C
1
соответственно. Пусть B
1
лежит между A и B. Обозначим
через K точку пересечения прямой B
1
C
1
с прямой, проведенной
через точку B параллельно AY . Тогда
S
OB
1
B
= S
OKB
− S
B
1
KB
< S
OKB
= S
OCC
1
.
Следовательно, S
ABC
< S
AB
1
C
1
. Случай, когда точка B лежит
между точками A и B
1
рассматривается аналогично.
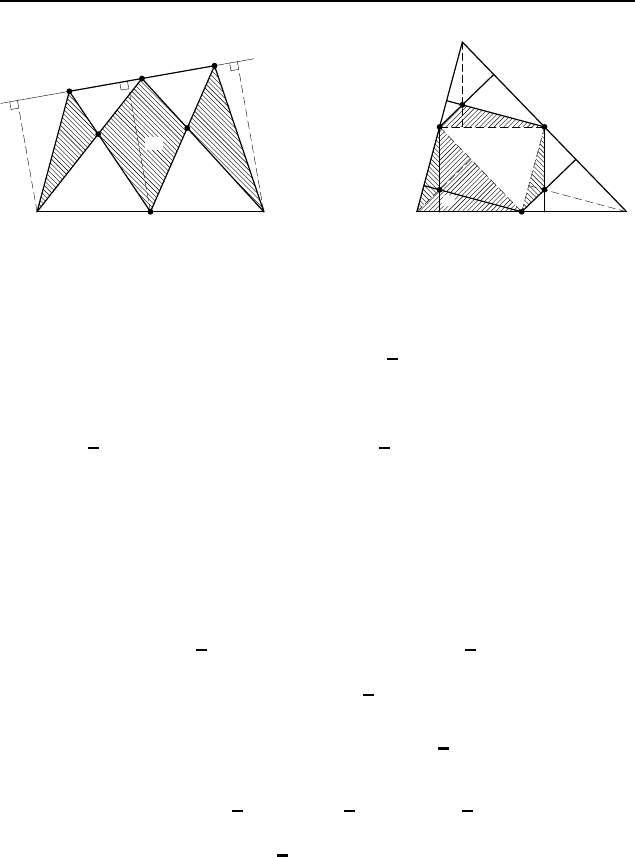
2.509. Отрезок, соединяющий середины оснований.
Пусть P и Q — середины оснований BC и AD трапеции
ABCD (рис. 401, а), h — высота трапеции. Если точка X
принадлежит отрезку P Q, то XP и XQ — медианы треуголь-
ников BXC и AXD, поэтому S
XBP
= S
XCP
и S
XAQ
= S
XDQ
.
Кроме того,
S
ABP Q
=
1
2
(BP + AQ) · h =
1
2
(CP + DQ) · h = S
CP QD
.
Следовательно, S
XAB
= S
XCD
.
Пусть теперь X — точка внутри трапеции ABCD, для кото-
рой S
XAB
= S
XCD
(рис. 401, б ). Предположим, что X не лежит
X
A
B C
D
P
Q
а)
A
B C
D
P
Q
X
б )
Рис. 401
310 8 класс
P
Q
h
1
h
2
h
3
A
B
C
D
M
N
Рис. 402
M
N
A
A
1
B
B
1
C
C
1
K
Рис. 403
на прямой P Q. Поскольку S
XBP
= S
XCP
и S
XAQ
= S
XDQ
, то
S
ABP XQ
= S
CP XQD
=
1
2
S
ABCD
.
Если точки X и C лежат по одну сторону от прямой P Q, то
1
2
S
ABCD
= S
ABP Q
+ S
P XQ
=
1
2
S
ABCD
+ S
P XQ
,
что невозможно. Аналогично для случая, когда точки X и C
лежат по разные стороны от прямой P Q.
2.510. Обозначим расстояния от точек A, N и D (рис. 402)
до прямой BC через h
1
, h
2
и h
3
соответственно, а площади тре-
угольников BP M и CQM — через x и y. Тогда
S
AP B
+ x =
1
2
BM ·h
1
, S
CQD
+ y =
1
2
CM · h
3
,
S
MP N Q
+ x + y =
1
2
BC · h
2
.
По теореме о средней линии трапеции h
2
=
1
2
(h
1
+ h
3
). Поэтому
S
AP B
+ S
CQD
+ x + y =
1
2
BM ·h
1
+
1
2
CM ·h
3
=
1
2
CM ·(h
1
+ h
3
) =
= CM · h
2
=
1
2
BC · h
2
= S
BNC
= S
MP N Q
+ x + y.
Следовательно,
S
AP B
+ S
CQD
= S
MP N Q
.
2.511. Пусть A
1
, B
1
, C
1
— середины сторон BC, AC, AB
остроугольного треугольника ABC (рис. 403); пусть также
