Гордин Р.К. Геометрия. Планиметрия. 7-9 классы

Подождите немного. Документ загружается.

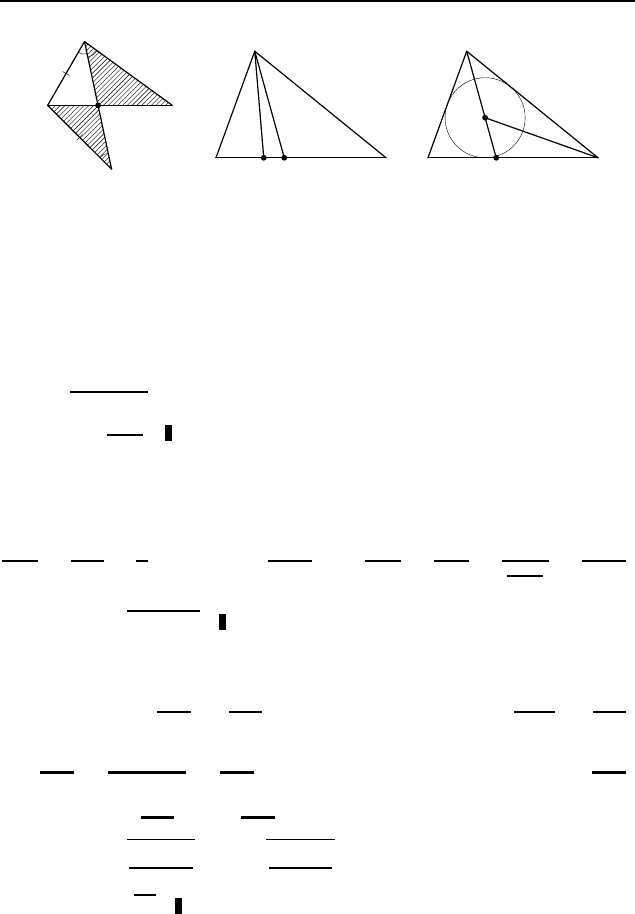
§ 2.9 321

Рис. 429

B CDD

Рис. 430

A B

Рис. 431

треугольник CAK — равнобедренный, AK = AC. Из подобия

треугольников ADK и BDC следует, что AK : BC = AD : DB,

а так как AK = AC, то AC : BC = AD : DB.

2.575

. Если AD

— биссектриса треугольника ABC

(рис. 430), то BD

: AB = D

C : AC, откуда BD

= BC ·

AB+AC

= BD. Следовательно, точки D и D

совпадают.

2.576.

a+b

Пусть CK — биссектриса треугольника ABC,

O — центр вписанной окружности (рис. 431). Тогда BO —

биссектриса треугольника BCK. По свойству биссектрисы тре-

угольника

, BK =

a + b

a+b

a + b

2.577.

b(b + c). Поскольку треугольник ADB — рав-

нобедренный, то ∠ABC = ∠BAD = ∠DAC (рис. 432). Сле-

довательно, треугольники ADC и BAC подобны (по двум уг-

лам). Поэтому

. Следовательно, DC =

С другой стороны, по свойству биссектрисы треугольника име-

ем:

AC+AB

b+c

. Отсюда находим, что DC = BC

b+c

Из равенства

= BC

b+c

следует, что BC

= b(b + c).

2.578.

или

+2b

2.579

√

ab. Пусть вписанная окружность касается боко-

вой стороны AB трапеции ABCD в точке M, а боковой сторо-

ны CD — в точке N. Центр O этой окружности расположен на

средней линии P Q трапеции (точка Q — середина CD), а про-

екция K точки O на MN — середина MN (рис. 433). Поскольку

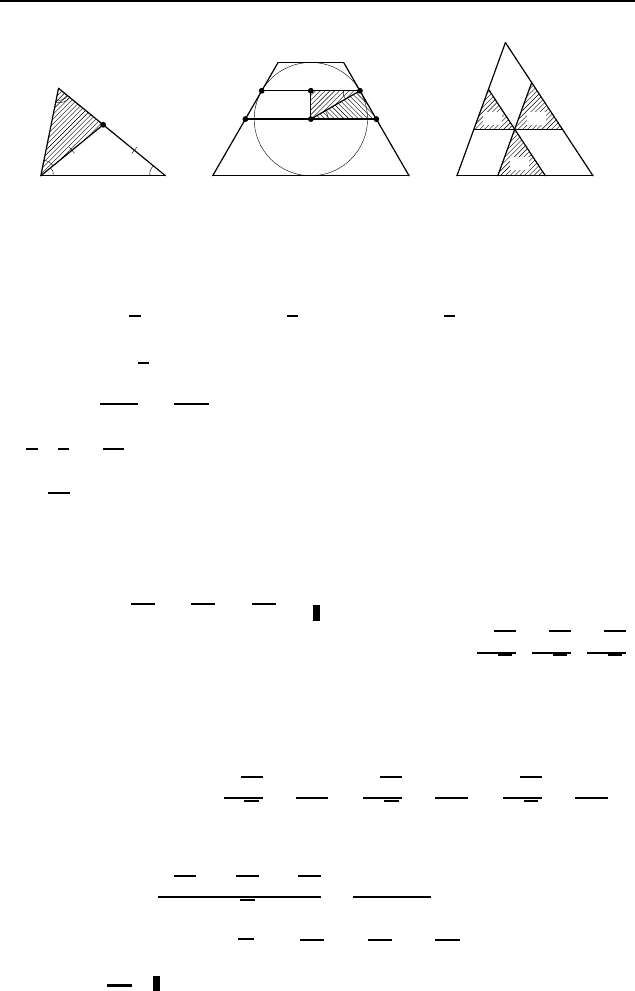
322 8 класс

A B

Рис. 432

B C

Рис. 433

B C

Рис. 434

трапеция описана около окружности,

P Q =

(AD + BC) =

(AB + CD) =

(a + a) = a.

Тогда OQ =

. Из подобия треугольников OKN и QNO сле-

дует, что

, откуда находим, что ON

= OQ · KN =

. Поскольку ON — радиус вписанной окружности,

а высота данной трапеции равна диаметру, то эта высота рав-

на

√

ab.

2.580. 2. Указание. Данная касательная отсекает от тре-

угольника подобный ему треугольник с коэффициентом, рав-

ным отношению их периметров.

2.581. (

√

)

. Каждый из образованных тре-

угольников подобен данному с коэффициентом

√

где S — искомая площадь данного треугольника ABC (рис. 434).

Обозначим стороны этих треугольников, соответствующие сто-

роне BC треугольника ABC, через a, b и c соответственно. Тогда

a + b + c = BC и

√

Сложив почленно последние три равенства, получим:

√

a + b + c

= 1.

Отсюда находим, что

√

S =

√

2.582.

Пусть ABC — данный треугольник. Обозна-

чим указанные точки деления, как показано на рисунке 435.

§ 2.9 323

Рис. 435

Рис. 436

Тогда S

. Пусть F — точка пересечения прямых C

и AC; MNKLP Q — указанный шестиугольник. Из равенства

треугольников F A

C и C

следует, что CF = C

AC = CB

. Из подобия треугольников A

и B

находим, что

. Аналогично,

. Поэто-

му S

. Аналогично, S

= S

P Q

Следовательно,

MN KLP Q

− 3 ·

−

2.583. 1 : 1.

2.584

Пусть K — точка пересечения отрезков AA

и BB

(рис. 436). Через точку B проведем прямую, параллель-

ную AC, и продолжим AA

до пересечения с этой прямой в точ-

ке T . Треугольники BA

T и CA

A подобны с коэффициентом 2.

Поэтому BT = 2AC = 6AB

, а из подобия треугольников BKT

и B

KA находим, что

= 6. Поэтому

ABB

· S

ABC

Аналогично находим, что S

BMC

= S

CNA

, где M — точка

пересечения BB

и CC

, а N — AA

и CC

. Следовательно,

MN K

= S

ABC

−S

ABB

−S

BCC

−S

CAA

+ S

AKB

+ S

BMC

+ S

CNA

= 1 −

−

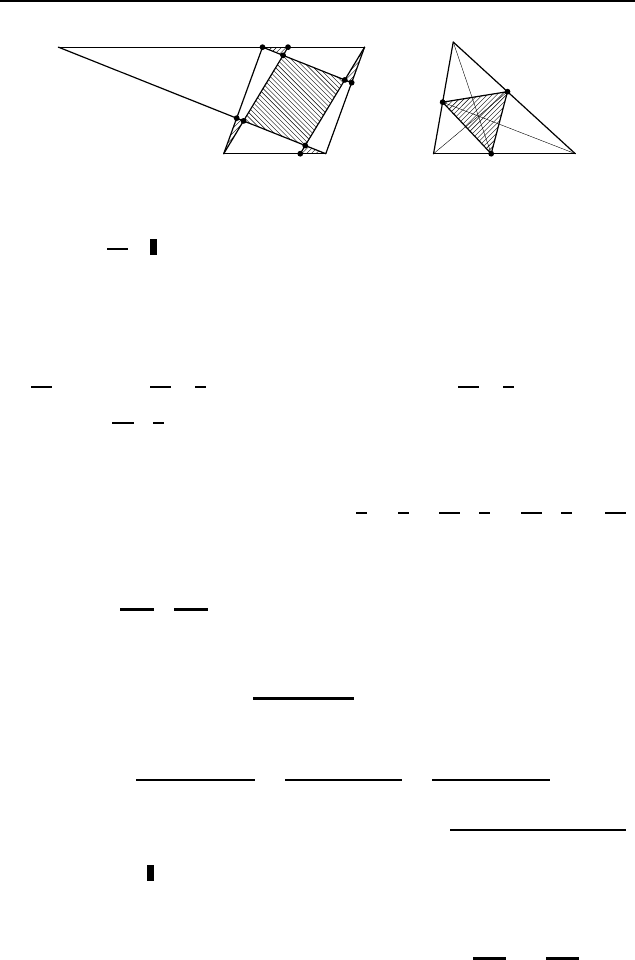
324 8 класс

B C

Рис. 437

B C

Рис. 438

2.585.

Пусть P — точка пересечения отрезков AN

и BK, Q — BK и CL, T — CL и DM, R — AN и DM (рис. 437).

Продолжим DM до пересечения с продолжением CB в точ-

ке O. Из подобия образовавшихся треугольников OMB и DMA,

OT C и DT L находим, что CT : T L = 12 : 1. Поэтому S

DT L

CLD

. Аналогично, S

BP N

и S

CKQ

= S

ARM

. Следовательно,

P QT R

= S

ABCD

− 2S

BCK

− 2S

ABN

+ 2S

BP N

+ 2S

ARM

= 1 −

−

2.587. Пусть AM, BN и CK — биссектрисы треугольни-

ка ABC и AB = c, AC = b и BC = a (рис. 438). Если S

ABC

= S,

то S

AKN

· S. По свойству биссектрисы треугольни-

ка AK : KB = AC : BC = b : a и AN : N C = AB : BC = c : a.

Поэтому AK : AB = b : (a + b) и AN : AC = c : (a + c).

Следовательно, S

AKN

bcS

(a+b)(a+c)

. Аналогично для треуголь-

ников BKM и CM N. Тогда

KMN

= S −

bcS

(a + b)(a + c)

−

acS

(a + b)(b + c)

−

abS

(a + c)(b + c)

2abcS

(a + b)(a + c)(b + c)

2.588. 60.

Треугольник ABD равнобедренный, так как

его биссектриса BF является высотой (рис. 439). Поэтому AF =

= F D и S

AF E

= S

DF E

= 5. Кроме того, BC = 2BD = 2AB.

Тогда по свойству биссектрисы треугольника

= 2.

Следовательно, S

DEC

= 2S

ADE

= 4S

DEF

= 20, а S

ADC

= 30.

Поэтому S

ABC

= 2S

ADC

= 60.

§ 2.9 325

BC D

Рис. 439

B C

Рис. 440

Рис. 441

2.589. Из условия задачи следует, что

ODC

BOC

AOD

ODC

, по-

этому

(рис. 440). Значит, треугольники BOC и DAO

подобны. Следовательно, ∠BCO = ∠DAO. Поэтому BC k AD.

2.590. Пусть точки A и B лежат на прямой l (рис. 441).

Возьмем точку M так, чтобы точки M и A лежали по разные

стороны от прямой l

. Пусть отрезки MA и MB пересекают

прямую l

соответственно в точках A

и B

. Обозначим через P

точку пересечения диагоналей AB

и BA

трапеции AA

Тогда прямая MP делит отрезок AB пополам (замечательное

свойство трапеции).

2.591. Пусть сначала точка M и прямая l лежат по разные

стороны от прямой l

(рис. 442). Возьмем на на прямой l две

точки A и B. Пусть A

и B

— точки пересечения MA и MB

с прямой l

, P — точка пересечения диагоналей AB

и BA

трапеции AA

B, K и Q — точки пересечения прямой MP

с A

и AB соответственно. Если T — точка пересечения пря-

мых AK и QB

, то прямая T M — искомая. Действительно,

поскольку A

K = KB

, то

T B

T Q

, по-

этому

. Следовательно, MT k KB

k l.

Если точка M лежит внутри полосы между прямыми l и l

то через произвольную точку M

, лежащую вне этой полосы,

проведем прямую l

, параллельную прямым l

и l (указанным

выше способом), а затем через точку M проведем прямую, па-

раллельную прямым l

и l

2.593. 3.

Треугольники ABD и ACD равновелики

(рис. 443), так как S

ABD

= S

ABE

+ S

AED

= S

DCE

+ S

AED

= S

ACD

. Тогда их высоты, опущенные на общее основание AD,

равны. Следовательно, BC k AD. Поэтому треугольники BEC

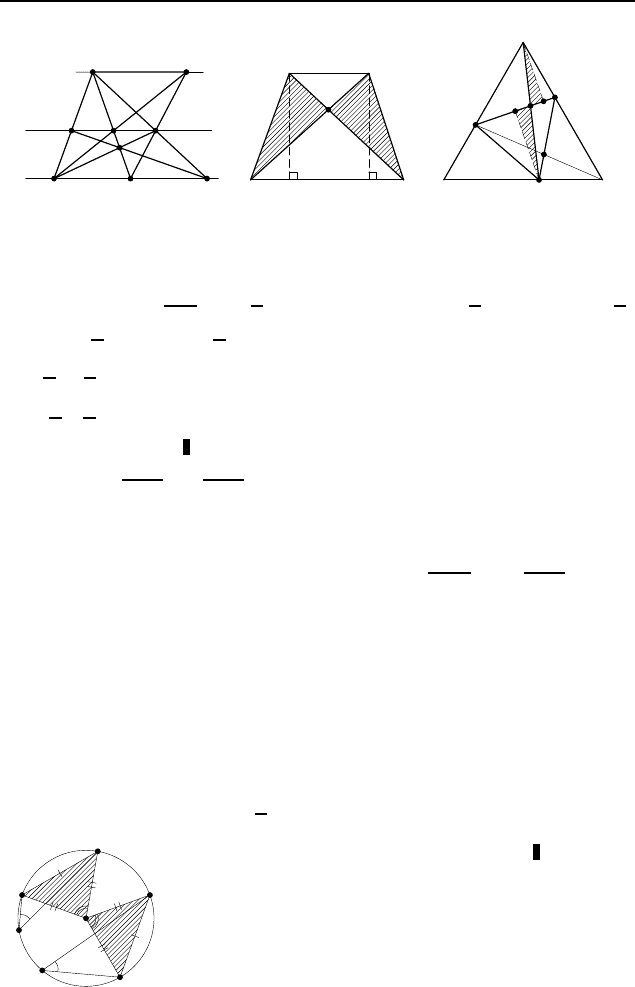
326 8 класс

Рис. 442

B C

Рис. 443

Рис. 444

и DEA подобны. Обозначим BC = x. Тогда коэффициент

подобия равен

. Имеем S

BEC

· S

DEC

DEA

· S

ABE

. По условию задачи S

BEC

+ S

DEA

6 2,

т. е.

6 2, но для любого положительного x верно неравен-

ство

> 2, причем равенство достигается, только если x = 3.

2.594. 1 + 3k.

Если Q — точка пересечения отрезков AA

и C

, то

= k (рис. 444). Аналогично для точ-

ки пересечения отрезков CC

и A

. Опустим из точек B

и B

перпендикуляры BM и B

N на прямую A

. Тогда

треугольники BMO и B

NO подобны,

= k.

Поэтому S

= kS

. Аналогично получим равен-

ства S

= kS

и S

= kS

. Следовательно,

ABC

= S

+ 3kS

= (1 + 3k)S

§ 2.10

2.595. 30

◦

, 60

◦

, 90

◦

. 2.596. а) 60

◦

, 65

◦

, 55

◦

; б) 20

◦

, 55

◦

, 105

◦

Рис. 445

2.597. 40

◦

, 80

◦

, 60

◦

или 20

◦

, 100

◦

, 60

◦

. 2.598. 35

◦

, 55

◦

. 2.599. 8,

4, 4

√

3. 2.600. 96

◦

, 132

◦

, 84

◦

, 48

◦

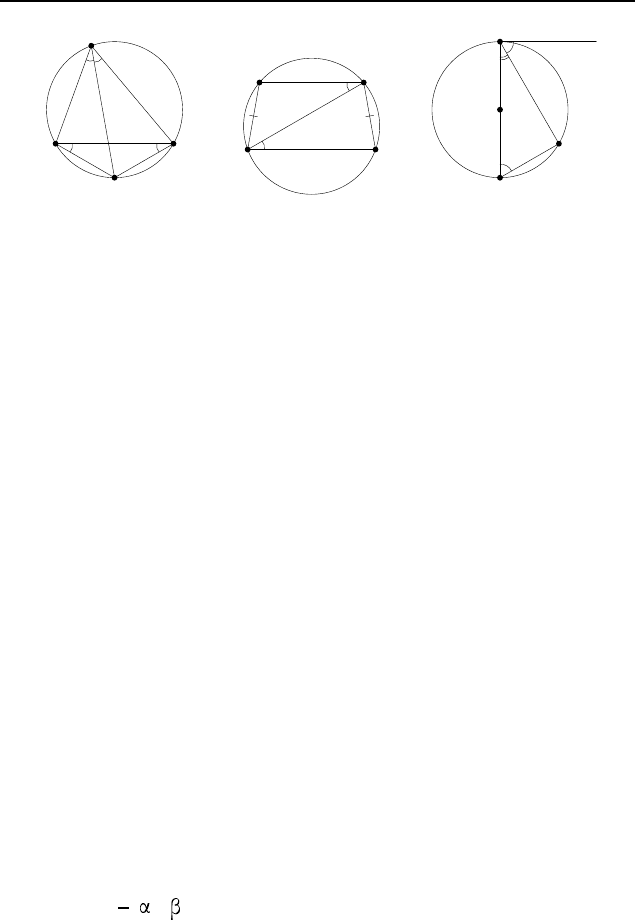
2.601

. Обратное неверно.

Пусть

точки A, B, C, A

, B

, C

лежат на окруж-

ности с центром O и ∠BAC = ∠B

(рис. 445). Тогда равны и соответствующие

центральные углы, т. е. ∠BOC = ∠B

значит, равны равнобедренные треуголь-

ники BOC и B

. Следовательно,

§ 2.10 327

Рис. 446

B C

Рис. 447

Рис. 448

BC = B

. Если два вписанных угла опираются на равные

хорды то они либо равны, либо составляют в сумме 180

◦

2.602. BM = CM как хорды, на которые опираются равные

вписанные у глы (рис. 446).

2.603

. Пусть трапеция ABCD с основаниями BC и AD

вписана в окружность (рис. 447). Тогда вписанные углы ACB

и CAD равны как накрест лежащие углы, образованные парал-

лельными прямыми BC и AD и секущей AC. Следовательно,

равны и хорды, на которые они опираются , т. е. AB = CD.

2.604. 60

◦

, 120

◦

, 60

◦

, 120

◦

. Указание. Соедините центр

окружности с вершинами меньшего основания трапеции. Три

полученных треугольника равны по трем сторонам.

2.606

. Если указанный угол прямой, то утверждение оче-

видно, так как в этом случае хорда является диаметром. Пусть

угол между касательной AC и хордой AB острый (рис. 448).

Проведем диаметр AD. Тогда углы BAC и ADB равны, так как

каждый из них в сумме с углом BAD составляет 90

◦

. Но

угол ADB равен половине дуги AB, заключенной между ка-

сательной AC и хордой AB. Если угол CAB тупой, то его

смежный угол острый, значит, он равен половине дуги AB, не

содержащей точку D. Следовательно, угол CAB равен половине

оставшейся ду ги.

2.607. 110

◦

, 250

◦

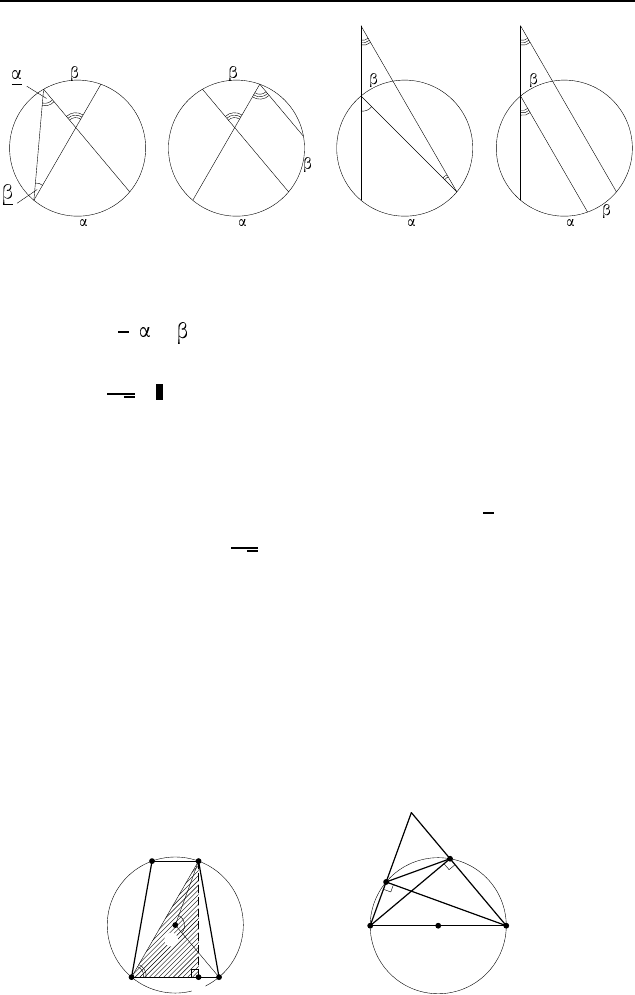
2.608

(

+ ). Указание. Первый с пособ. Соедините концы

двух хорд и рассмотрите внешний угол полученного треуголь-

ника (рис. 449, а).

Второй способ. Через конец одной хорды проведите прямую,

параллельную второй хорде (рис. 449, б ).

328 8 класс

а)

б )

Рис. 449

а) б )

Рис. 450

2.609

(

− ). Указание. См. рис. 450, а и 450, б .

2.610. 540

◦

2.611.

√

Пусть O — центр окружности, описанной око-

ло равнобокой (см. задачу 2.603

) трапеции ABCD с основа-

ниями AD и BC (рис. 451). Если H — проекция вершины C на

большее основание AD, то отрезок AH равен средней линии тра-

пеции (см. задачу 2.118

), а так как ∠CAD =

∠COD = 60

◦

то AH = CH ctg 60

◦

√

2.612. Указание. Примените теорему о средней линии тре-

угольника.

2.613

. Поскольку отрезок AB виден из точек A

и B

под

прямым углом (рис. 452), эти точки лежат на окружности с

диаметром AB. Поэтому

∠CA

= 180

◦

− ∠BA

= ∠CAB.

Рис. 451

Рис. 452

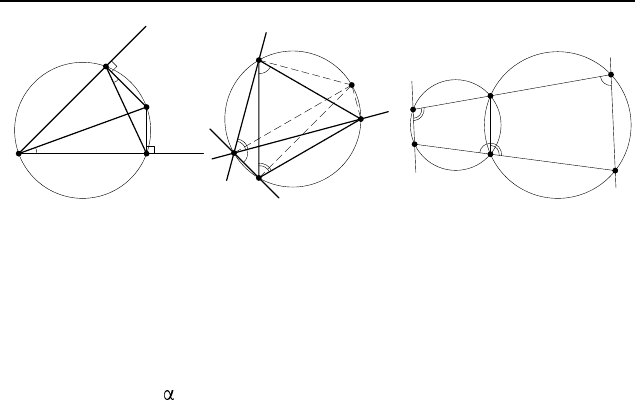
§ 2.10 329

Рис. 453

Рис. 454

Рис. 455

2.614. Поскольку отрезок AP виден из точек B

и C

под

прямым углом, то точки C

и B

лежат на окружности с диа-

метром AP (рис. 453). Следовательно, ∠C

AP = ∠C

P .

2.615. 80

◦

2.616. 90

◦

2.617. Пусть точка M расположена, как показано на рисун-

ке 454; A

, A

— проекции точки M на данные прямые.

Поскольку отрезок OM виден из точек A

, A

под пря-

мым углом, то точки O, M, A

, A

лежат на окружности с

диаметром OM. Тогда ∠A

= ∠A

= 60

◦

и ∠A

= ∠A

= 60

◦

2.618. Указание. Дуги AC и AD равны, так как они сим-

метричны относительно диаметра AB.

2.619. Пусть отрезки CE и F D не пересекаются (рис. 455).

Соединим точки A и B. Поскольку

∠ABD = 180

◦

− ∠C, ∠ABF = 180

◦

− ∠ABD,

то ∠ABF = ∠C, а так как ∠AEF = 180

◦

− ∠ABF , то ∠CEF +

+∠C = 180

◦

. Следовательно, CD k EF . Аналогично для случая,

когда отрезки CE и F D пересекаются.

2.620. Каждый из двух смежных углов MQN и MQL

(где Q — точка пересечения хорд) равен полусумме соответ-

ствующих дуг (рис. 456).

2.621. Пусть окружность, проходящая через точки A и B

(рис. 457), касается второй стороны угла с вершиной O в

точке M, а K — произвольная точка луча OM, отличная

от M. Поскольку точка K лежит вне окружности, отрезок AK

330 8 класс

Рис. 456

Рис. 457

Рис. 458

пересекает окружность в некоторой точке P . Поэтому

∠AMB = ∠AP B > ∠AKB.

2.622. Пусть биссектриса угла BM C пересекает окружность

в точках P и R, а биссектриса угла BNA — в точках Q и S

(рис. 458). Тогда

AS − DQ = BS − CQ и DR − CP = AR − BP

(см. задачу 2.609

), или

BS + DQ = AS + CQ и AR + CP = DR + BP.

Следовательно,

AS + AR+ CP + CQ = BS + BP + DR+ DQ = 180

◦

Поэтому угол между хордами P R и SQ равен 90

◦

(см. зада-

чу 2.608

2.623

. Обозначим ∠A =

, ∠B = (рис. 459). Тогда

∠BOM = ∠ABO + ∠BAO =

∠OBM = ∠OBC + ∠CBM = ∠OBC + ∠MAC =

Следовательно, ∠BOM = ∠OBM. Аналогично, ∠MCO =

= ∠MOC.