Горлач В.В. и др. Лабораторный практикум по колебательным и волновым процессам
Подождите немного. Документ загружается.

Если прибор имеет симметричную шкалу с нулём посредине, то следуя
(П.1.4), получаем θ
a
=К∙2a
max
/100. Для большинства распространённых приборов,
на шкале которых нуль находится у левого конца, т. е. a
min
= 0, погрешность
вычисляется по формуле
θ
a
= . (П.1.5)
При измерении прибором с неизвестным классом точности системати-
ческая погрешность принимается равной цене деления.
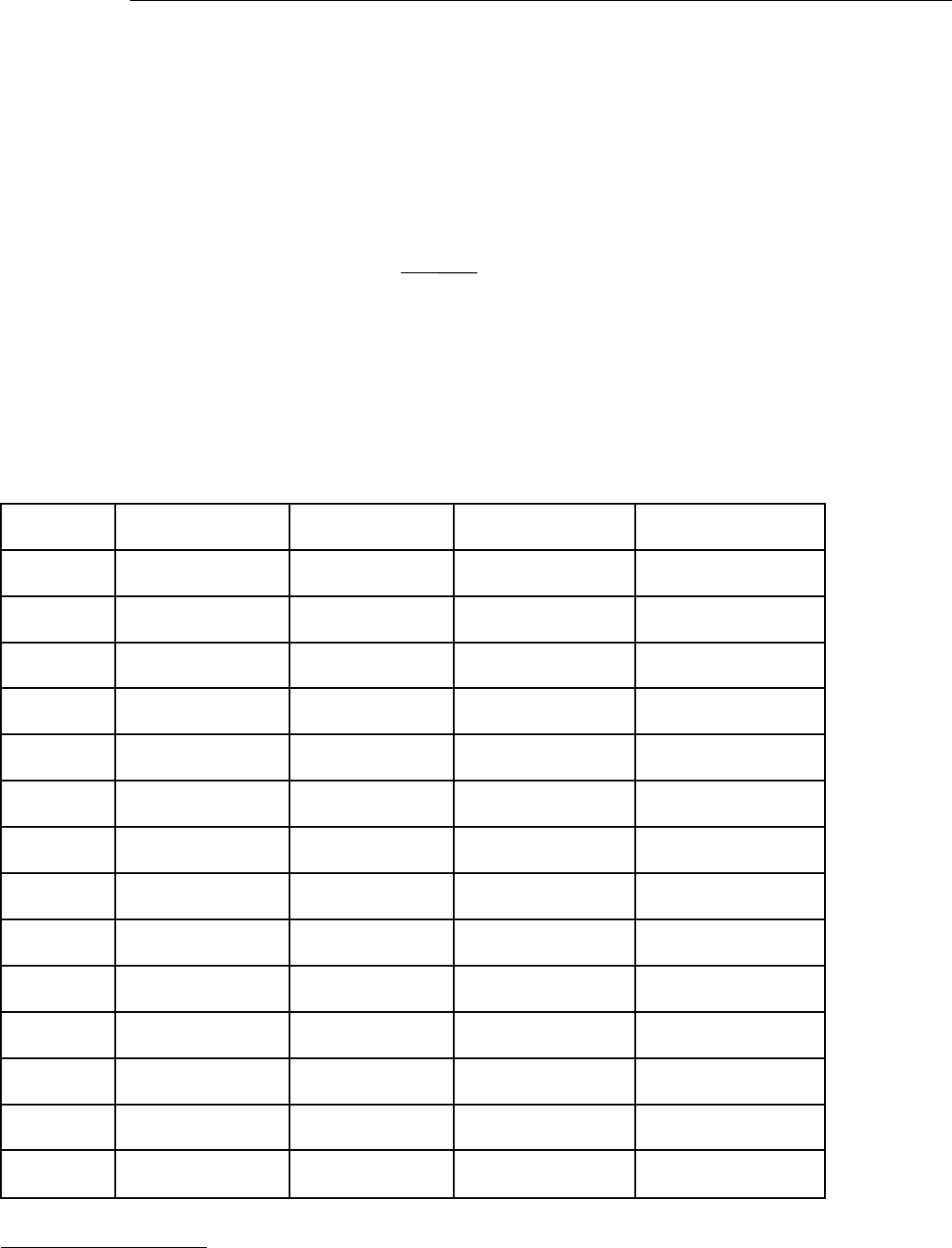
Таблица П.1.1
Коэффициенты Стьюдента t
P, n
(n – число измерений; Р – доверительная вероятность
74
)
n Р = 0,900 Р = 0,950 Р = 0,990 Р= 0,999
3 2,920 4,303 9,925 31,60
4 2,353 3,182 5,841 12,94
5 2,132 2,766 4,604 8,610
6 2,015 2,571 4,032 6,859
7 1,943 2,447 3,707 5,959
8 1,895 2,365 3,499 5,405
9 1,860 2,306 3,355 5,041
10 1,833 2,262 3,250 4,781
11 1,812 2,228 3,169 4,587
12 1,796 2,201 3,106 4,437
15 1,751 2,145 2,977 4,140
20 1,729 2,093 2,861 3,883
30 1,699 2,045 2,756 3,659
∞
1,645 1,960 2,576 3,291
74 Значение доверительной вероятности, с которой рекомендуется представлять результаты
многократных измерений, Р = 0,95. Исключения составляют случаи: 1) когда границы
доверительного интервала заранее определены техническими условиями; 2) в особо
ответственных измерениях (тогда Р > 0,95). Более полную таблицу коэффициентов Стьюдента
можно найти в справочнике [8].
111
100
К∙ a
max
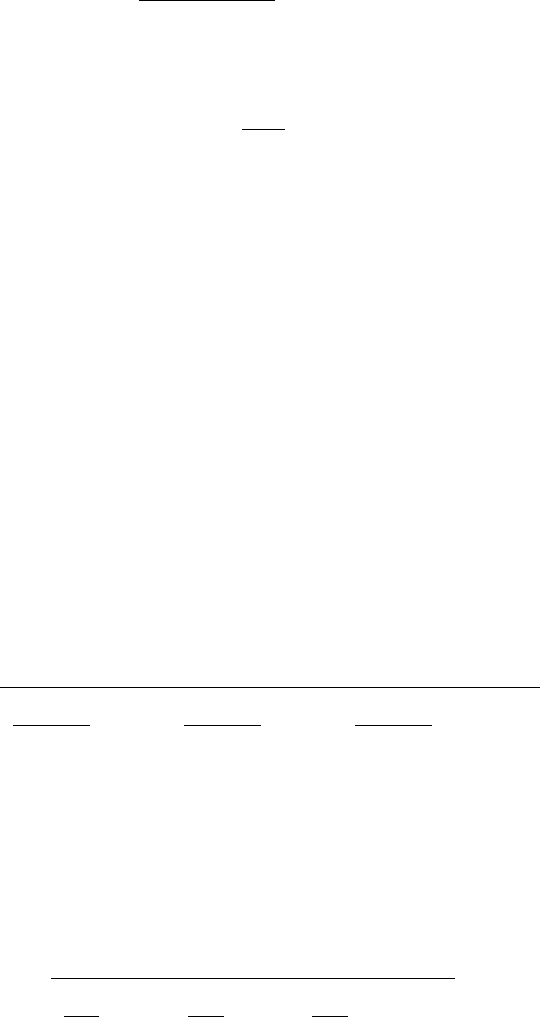
5. Вычислить абсолютные погрешности Δa, Δb, Δc, … прямых
многократных измерений. Абсолютная погрешность Δa представляет собой
геометрическую сумму случайной Δ
a
и систематической θ
a
составляющих
a =
a
2
θ
a
2
, Р = 0,95. (П.1.6)
6. Найти относительные погрешности δ
a
, δ
b
, δ
c
, …
a
=
a
a
. (П.1.7)
7. Записать результаты каждого из прямых измерений в виде (П.1.1):
a = 〈 a〉 ± a , P = 0,95.
Абсолютную погрешность Δa округляют до двух значащих цифр, если
первая значащая цифра 1 или 2, а когда первая цифра 3, 4, ... 9, тогда до одной
значащей цифры.
Среднее значение
〈 a〉
округляют так, чтобы последние цифры в числовых
значениях
〈 a〉
и
a
находились в одном разряде.
Примеры: m = (224,7 ± 1,4)·10
-3
кг, Р = 0,95;
ℓ = (43,20 0,03) мм, Р = 0,95.
8. Рассчитать абсолютную погрешность Δy косвенного измерения одним из
двух методов:
8.1. Дифференцирование натурального логарифма функции
y = f a ,b ,c ,...
.
Вычисляем сначала относительную погрешность
y
=
∂ln y
∂a
a
2
∂ln y
∂ b
b
2
∂ln y
∂с
c
2
...
, (П.1.8)
а затем – абсолютную
Δy =
y
⋅〈 y 〉
. (П.1.9)
8.2. Непосредственное дифференцирование функции
y = f a ,b ,c ,...
.
Этим методом сразу вычисляем абсолютную погрешность
y =
∂ y
∂ a
a
2
∂ y
∂ b
b
2
∂ y
∂ c
c
2
...
. (П.1.10)
Если некоторые из величин в (П.1.8) или (П.1.10) непосредственно не
измерялись в данном эксперименте, а их значения взяты из справочных таблиц,
то погрешности этих величин принимаются равными половине единицы
наименьшего разряда числа, представленного в таблице.
Примеры: ρ = 1,0 г/см
3
, Δρ = 0,05 г/см
3
.
π = 3,1415, ∆π = 0,00005.
112
9. Числовые значения
〈 y 〉
и
y
выразить в единицах СИ и представить
окончательный результат косвенного измерения в виде (П.1.1)
y =
〈 y 〉 ± y
, Р = 0,95.
В табл. П.1.2 приведены результаты применения формул (П.1.8) – (П.1.10)
к некоторым простым функциям.
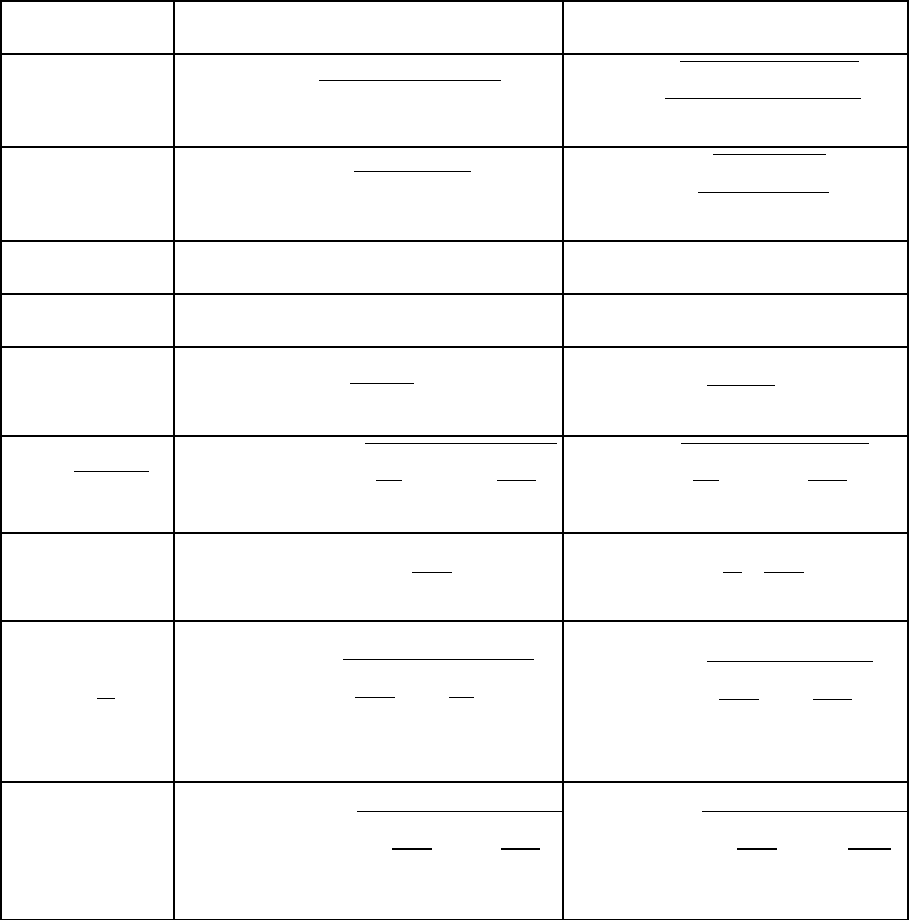
Таблица П.1.2
Основные формулы погрешностей косвенных измерений
Функция Абсолютная погрешность Относительная погрешность
y=abc
y =
a
2
b
2
c
2
δ
y
=
a
2
b
2
c
2
abc
y = a – b
y =
a
2
b
2
δ
y
=
a
2
b
2
a−b
y = sin a Δy = cos a ·Δa δ
y
= ctg a ·Δa
y = cos a Δy = sin a ·Δa δ
y
= tg a ·Δa
y = tg a
y =
1
cos
2
a
⋅a
y
=
2
sin 2a
⋅ a
y =
a
a−b
y = y
2
b
a
2
a
2
b
a
2
y
=y
b
a
2
a
2
b
a
2
y = ln a
y =
a
a
y
=
1
y
⋅
a
a
y=
a
b
y =
a
b
2
a
b
2
b
2
δ
y
=
a
a
2
b
b
2
y = a
m
ּ b
n
y = y
m
a
a
2
n
b
b
2
y
=
m
a
a
2
n
b
b
2
113
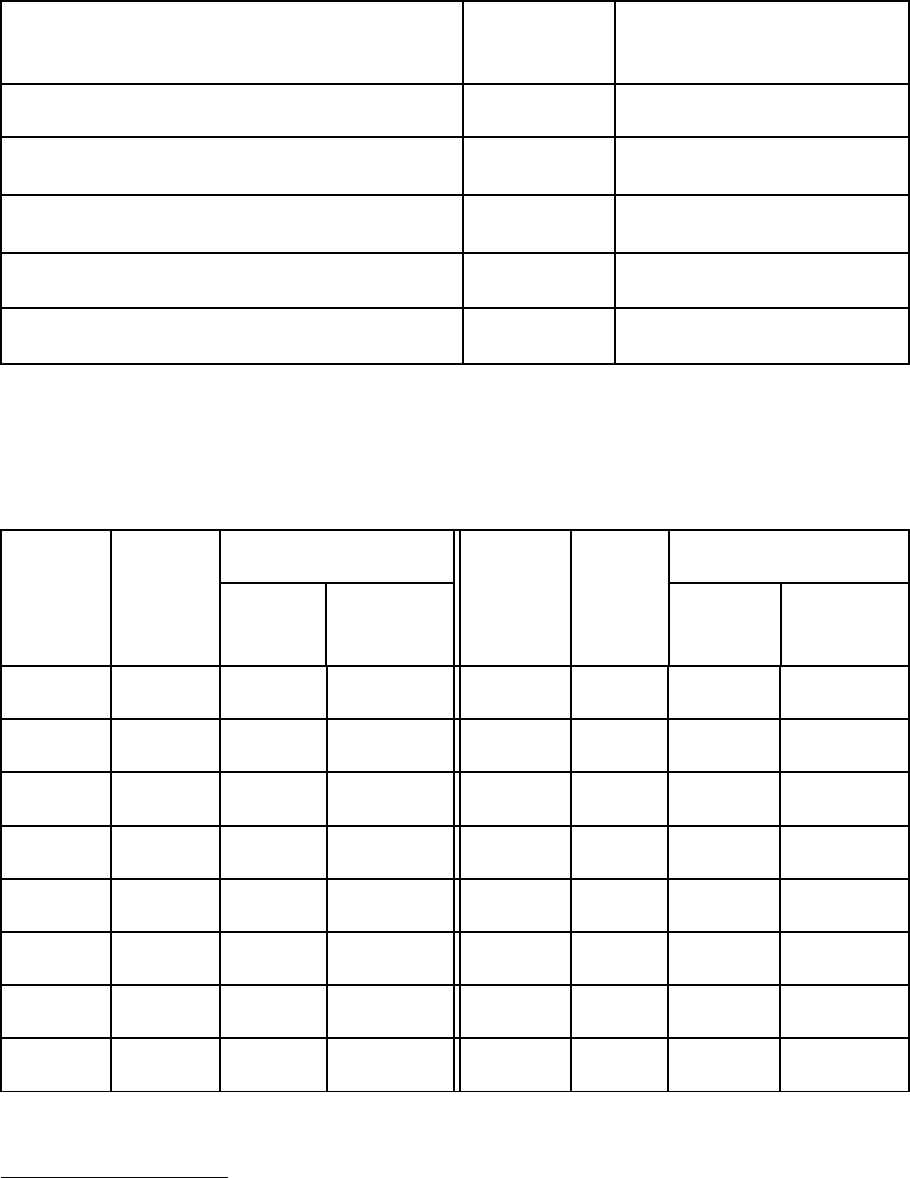
Приложение 2
Физические постоянные (по ГСССД 1-87 и CODATA, 1998)
75
Физическая постоянная
Обозна-
чение
Численное значение
Скорость света в вакууме с с = 299 792 458 м/с
Электрическая постоянная
ε
0
8,854187817·10
-12
Ф/м
Магнитная постоянная
μ
0
4
π
⋅10
-7
Гн/м
Постоянная Больцмана k
1,3806503·10
-23
Дж/К
Молярная газовая постоянная R
8,314472 Дж/(моль·К)
Приложение 3
Множители и приставки для образования кратных и дольных единиц
Множи-
тель
При-
ставка
Обозначение
русское
междуна-
родное
Множи-
тель
При-
ставка
Обозначение
русское
междуна-
родное
10
-18
атто а a 10
1
дека да da
10
-15
фемто ф f 10
2
гекто г h
10
-12
пико п p 10
3
кило к k
10
-9
нано н n 10
6
мега М M
10
-6
микро мк μ 10
9
гига Г G
10
-3
милли м m 10
12
тера Т T
10
-2
санти с c 10
15
пета П P
10
-1
деци д d 10
18
экса Э E
75 Таблицы стандартных справочных данных. Фундаментальные физические константы.
ГСССД 1-87. – М.: Изд-во стандартов, 1989.
CODATA — Комитет по численным данным для науки и техники Международного совета
научных организаций.
114
Библиографический список
1. Бондарев Б.В. Курс общей физики: в 3 кн. Кн.1. Механика [Текст]
/Б.В. Бондарев, Н.П. Калашников, Г.Г. Спирин. – М.: Высшая школа, 2005.
– 352 с.
2. Бондарев Б.В. Курс общей физики: в 3 кн. Кн. 2. Электромагнетизм.
Оптика. Квантовая физика [Текст] /Б.В. Бондарев, Н.П. Калашников,
Г.Г. Спирин. – М.: Высшая школа, 2005. – 438 с.
3. Валишев М.Г. Курс общей физики [Текст] /М.Г. Валишев, А.А. Повзнер.
– СПб.: Лань, 2009. – 579 с.
4. Горлач В.В. Обработка, представление, интерпретация результатов
измерений: учебное пособие [Текст] /В.В. Горлач, В.Л. Егоров, Н.А. Ива-
нов / под ред. В.В. Горлача. – Омск: Изд-во СибАДИ, 2006. – 83 с.
5. Горлач В.В. Физика: СРС: учебное пособие [Текст] /В.В. Горлач,
Н.А.Иванов, М.А. Пластинина /под ред. В.В. Горлача. – Омск: Изд-во
СибАДИ, 2009. –168 с.
6. Детлаф А.А. Физика [Текст] /Б.М. Яворский, А.А. Детлаф. – М.: Акаде-
мия, 2005. – 720 с.
7. Ивлиев А.Д. Физика: учебное пособие [Текст] /А.Д. Ивлиев. – СПб.: Лань,
2008. – 672 с.
8. Корн Г. Справочник по математике для научных работников и инженеров
[Текст] /Г. Корн, Т. Корн. – М.: Наука,1973. – 832 с.
9. Крауфорд Ф. Волны. Берклеевский курс физики. Т. III. [Текст]
/Ф. Крауфорд. – М.: Наука, 1976. – 527 с.
10.Оптика. Методическое руководство к лабораторным работам по физике.
[Текст] /сост. Б.Л. Паклин, С.А. Стрельцов, А.М. Погорельский и др. –
Новосибирск: Изд-во НГТУ, 2004. – 57 с.
11. Реально-виртуальная лаборатория по физике «Электричество и
магнетизм»: Руководство по эксплуатации [Текст]. – Томск: ТГУСУР,
2005. – 11 с.
12.Робертсон Б. Современная физика в прикладных науках [Текст]/
Б. Робертсон.– М.: Мир, 1985. – 272 с.
13.Руководство к лабораторным работам по физике для II курса/ под ред.
Э.А. Майера [Текст]. – Омск: СибАДИ, 1977. – 162 с.
14.Савельев И. В. Курс общей физики: в 3 т. Т. 2. Электричество и магнетизм.
Волны. Оптика [Текст] /И.В. Савельев. – СПб.: Лань, 2007. – 496 с.
15.Трофимова Т. И. Курс физики [Текст] / Т.И. Трофимова.– М.: Академия,
2007. – 560 с.
16. Чертов А.Г. Физические величины (Терминология, определения, размер-
ности, единицы) [Текст] / А.Г. Чертов. – М.: Высшая школа, 1990. – 335 с.
115

Учебное издание
Лабораторный практикум
по колебательным и волновым процессам
Учебное пособие
Под редакцией В.В. Горлача
Иллюстрации, компьютерная вёрстка:
В.В.Горлача
Редактор Н.И. Косенкова
Подписано к печати 25.08.2010
Формат 60х90 1/16. Бумага писчая
Оперативный способ печати
Гарнитура Times New Roman
Усл. п.л. 7,5. Уч.-изд. л. 5,3
Заказ ___. Тираж 250 экз.
Цена договорная
Издательство СибАДИ
644099, Омск, ул. П. Некрасова, 10
Отпечатано в подразделении ОП издательства СибАДИ
116
