Graef M. Introduction to conventional transmission electron microscopy

Подождите немного. Документ загружается.

318 Dynamical electron scattering in perfect crystals

This equation describes how the amplitude in the plane z = 0 is modiﬁed in the

plane z = ; in other words, the equation describes how the electrons propagate

from one slice to the next, and hence this equation is known as the propagator

equation. The exponential of the differential operator

 is rather difﬁcult to

compute analytically. However, following [CVDOdBVL97] or [Kir98], for

example, we can make use of the properties of Fourier transforms to derive a much

simpler expression. For a beam incident along the z-direction, the second term in

the deﬁnition of

 vanishes, and the operator is written as

 =

iλ

4π



Consider the following relation (using the deﬁnition of the inverse Fourier

transform):

ψ(R) =



ψ(q)e

2πiq·R

dq,

where R is a two-dimensional direct space vector, and q is a 2D reciprocal space

vector. Since the Laplacian operator acts only on the direct space coordinates, we

can bring it inside the integral and we ﬁnd:

ψ(R) =

(−iπλq

)ψ(q)e

2πiq·R

dq. (5.39)

Next, we use the Taylor expansion (5.26):





ψ =





(

)

ψ.

The higher-order derivatives of ψ can be calculated by repeated use of

equation (5.39), and we ﬁnd





ψ(R) =





(−iπλq

)



ψ(q)e

2πiq·R

dq;

−πiλq

ψ(q)e

2πiq·R

dq.

Finally, we ﬁnd the important result:





ψ(R)

= e

−πiλq

ψ(q). (5.40)

The complicated exponential of a differential operator in direct space is equivalent

to multiplication by a simple phase factor in reciprocal space. We have already

seen that in reciprocal space the geometry-dependent factor is given by e

2πis



5.6 The direct space multi-beam equations 319

and this in turn means that

−πiλq

= 2πis

 → s

=−

λq

The second equality is valid for exact zone axis orientation and we leave it to the

reader to show that this relation is indeed correct.

We can gain some additional insight into the physical meaning of the propagator

term by using the convolution theorem of equation (5.40):



ψ = F

−1

−πiλq

⊗ ψ(R). (5.41)

Propagation from one slice to the next is thus equivalent mathematically to a con-

volution operation. The ﬁrst factor on the right-hand side can be rewritten as

−1

−πiλq

= e

iπ R

/λ

= e

πikR

/

= P



(R),

and we recognize the Fresnel propagator, which was introduced in Section 3.4.7.

5.6.3 Solving the full direct-space equation

If we subdivide the crystal into n layers or slices of thickness , then in the limit of

vanishing slice thickness we have

ψ(x, y, z

) = e



iσ V

···e



iσ V



iσ V

ψ(x, y, 0), (5.42)

where the number of pairs of exponentials increases with decreasing , such that the

product n = z

is constant. This relation is remarkably similar to equation (5.32).

Each slice can, in principle, have a different projected potential, reﬂected in the use

of the superscript n. The interpretation of this relation is rather simple: the scattering

process of a fast electron is broken up into two steps per crystal slice. The ﬁrst

involves multiplication with the phase grating term. The entire potential of the slice

is projected onto a plane normal to the beam direction, and, for a sufﬁciently thin

slice, the phase grating term changes only the phase of the electron wave function.

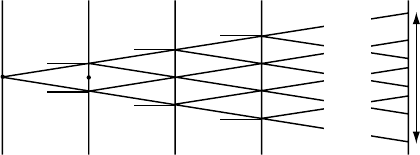
Then, the wave propagates to the next slice, as illustrated in Fig. 5.2. From the

starting point at (x, y, z) the electron can reach any point within a certain distance

w/2 from the point (x, y, z + ); the magnitude of this distance is determined by the

electron wavelength and the slice thickness in the form of the complex differential

operator 

. We will see in Chapter 7 that equations (5.32) and (5.42) form the basis

for fast numerical algorithms to compute the solution to the dynamical multi-beam

electron diffraction equations.

320 Dynamical electron scattering in perfect crystals

z = 0

ε2ε3ε

nε

x, y, 0

...

x ,y,

Fig. 5.2. Illustration of the propagation of an electron through consecutive slices of a crystal.

5.7 Bloch wave description

In Section 5.3, we have approached the electron scattering problem assuming that

electrons will travel only in the directions k

and k

+ g. While this is a valid

assumption for an external observer (who is interested mainly in the travel direction

of the electrons after they have left the crystal), it is not necessarily valid inside

the crystal. Let us consider a simple analogy: a sound wave – a compressive wave in

the medium “air” – enters a solid on one side and emerges from that solid on the

opposite side, ignoring reﬂection of the wave. We know that the only sound waves

possible inside a crystal with 3D periodicity are phonons (or quantized lattice

vibrations); thus, the sound wave will propagate through the crystal as a linear

superposition of phonons, each with its own frequency and energy. The relation

between frequency (or wave vector) and energy is called a dispersion relation.It

is possible that there are gaps in the dispersion function; this indicates that certain

frequencies are not transmitted by the crystal.

A similar situation occurs for high-energy electrons traveling through matter.

Before entering the crystal, the electron can travel with any wave vector.

†

Inside the

crystal, the allowed directions depend on the crystal structure and on the electron

energy. The problem of ﬁnding the allowed wave vectors inside a crystal is closely

related to another important solid-state problem: the band-structure of a material.

Band theory addresses the question: which electron energies are allowed for a

given wave vector (or electron momentum)? When the allowed energies are plotted

versus the wave vector, the so-called band-structure is obtained; certain energy

levels may be inaccessible to the electrons and form band-gaps. The width of a

band-gap is determined by the Fourier coefﬁcients of the lattice potential. We will

show in this section that the problem of electron diffraction is closely related to the

band-structure of a material. We will ask the question: for a given incident energy,

what are the allowed wave vectors inside the crystal? The incident energy is several

†

Wavelength and energy are related to each other by equation (2.33) of Chapter 2, which is therefore the dispersion

relation in vacuum, and the direction of the wave is arbitrary.

5.7 Bloch wave description 321

orders of magnitude larger than the typical energies of electrons in a solid, which

will lead to some qualitative differences between the two theories.

Most of the theory presented in this section is based on two important review

articles of the Bloch wave method: Diffraction of Electrons by Perfect Crystals,

by A.J.F. Metherell [Met75], and The Scattering of Fast Electrons By Crystals,by

C.J. Humphreys [Hum79]. We have adapted slightly the notation used in those

papers to conform with the remainder of this book, and also with the notation used

in the book Electron Microdiffraction, by J.C.H. Spence and J.M. Zuo [SZ92].

We start from equation (2.37): we expand the lattice potential in a Fourier series,

V (r) =



2πih·r

Once again, we separate the V

term from the rest of the potential and we will use

the refraction-corrected wave vector k

(see equation 5.4) throughout this section.

We do not include absorption at this point, so that the potential above is real, not

complex. The effect of absorption will be described in Section 5.7.3.

The electron wave inside the crystal is written as the product of a wave with arbi-

trary wave vector k (to be determined later) and a function C(r) with the periodicity

of the lattice. This type of wave function is known as a Bloch wave:

(r) = C(r)e

2πik·r



2πi(k+g)·r

, (5.43)

where we have introduced a Fourier expansion for C(r). Bloch waves were ﬁrst

introduced into quantum mechanics by Felix Bloch in 1929 [Blo29], for the elec-

tron theory of ferromagnetism. Note that, for a perfect crystal, the coefﬁcients C

are independent of position; this is different from expression (5.7), where the co-

efﬁcients ψ

do depend upon position. The coefﬁcients C

do, however, depend

on the wave vector k. A second important difference, as mentioned above, is that

an arbitrary wave vector k is used, instead of k

. The solution method described

below will enable us to determine the allowed wave vector(s) k for a given incident

beam energy. The coefﬁcients C

are called Bloch wave coefﬁcients.

Substitution of (r) into equation (5.5) leads to



− (k + g)



h=g

g−h



2πi(k+g)·r

= 0, (5.44)

which must be valid for any position r in the crystal. Therefore, we can write

− (k + g)



h=g

g−h

= 0. (5.45)

322 Dynamical electron scattering in perfect crystals

This set of equations, one for each g,isexact, i.e. no approximations have been

used so far. They relate the wave vector k of the Bloch wave to the energy of the

incident electron (through k

), hence they are dispersion relations.

5.7.1 General solution method

We now proceed to solve equations (5.45) for a multi-beam situation. We note that,

as before, the scattering problem naturally separates into two contributions: the

geometry of the problem is described in the ﬁrst term of (5.45), and the interaction

with the crystal potential in the second summation. The ﬁrst term can again be

represented by a diagonal matrix, while the second term only gives rise to off-

diagonal matrix elements. For convenience, we select the transmitted beam to be

the ﬁrst entry in the column vector of Bloch wave coefﬁcients, and the governing

equations (5.45) can then be rewritten in matrix form as







− k

0−g

... U

0−h

... U

0−m

g−0

− (k + g)

... U

g−h

... U

g−m

h−0

h−g

... k

− (k + h)

... U

h−m

m−0

m−g

... U

m−h

... k

− (k + m)



















= 0.

(5.46)

Non-trivial solutions can occur only when the determinant of this matrix is equal

to zero. It is easy to see that the leading term in this determinant is the product of

the main diagonal elements, and that this term is proportional to k

, where N is

the number of beams. All other contributions to the determinant contain only lower

powers of k. The resulting characteristic equation is then a polynomial equation of

order 2N , which must have 2N roots. We thus ﬁnd the important result that for an

N -beam case, the total number of allowed wave vectors inside the crystal is equal

to 2N.We will denote the different wave vectors by a superscript ( j), as in k

( j)

. The

most general wave solution inside the crystal therefore consists of a superposition

of 2N Bloch waves, each with its own amplitude α

( j)

(r) =



( j)



( j)

2πi(k

( j )

+g)·r



( j)

(r)e

2πik

( j )

·r

(5.47)

and the coefﬁcient α

( j)

is the excitation amplitude of the jth Bloch wave.

It may appear that we have introduced many more unknowns than equations; in

equation (5.47) we have 2N coefﬁcients α

( j)

,2N wave vectors k

( j)

, and 2N × N

Bloch wave coefﬁcients C

( j)

, for a total of 2N

+ 4N (complex) unknowns. In

5.7 Bloch wave description 323

the following paragraphs, we will show that we do have enough information to

determine all the unknown parameters unambiguously.

Since the total energy of the incident electron is constant, all 2N Bloch waves

must have the same total energy; we say that the Bloch waves are degenerate. Since

the 2N wave vectors k

( j)

are, in general, different from each other, each Bloch

wave must correspond to a different kinetic energy, and therefore also a different

potential energy. This, in turn, means that different Bloch waves must travel at

different locations through the crystal. This is a very important observation, and

we will return to it in the next chapter.

The 2N wave vectors k

( j)

are ranked according to decreasing kinetic energy.

This means that the Bloch wave with the highest kinetic energy is number (1), and

that corresponding to the lowest kinetic energy is number (2N). The reader should

be warned that in some of the earlier literature on the Bloch wave theory the wave

vector with the lowest kinetic energy was taken to be k

(1)

We deﬁne the unit vector n as the surface normal to the sample, in the direction

opposite

†

to the incident beam, i.e. along the −z-direction. Since both the incident

wave and the wave inside the crystal are solutions to the Schr¨odinger equation,

which is a second-order equation in the spatial coordinates, both the functions and

their ﬁrst-order derivatives must be continuous across the entrance plane of the

crystal. It can be shown quite generally (e.g. [Met75]) that this continuity condition

implies that the tangential component of the wave vector must be conserved across

the entrance plane. The only component of the wave vector that can change upon

entering the crystal is, therefore, the normal component. It is then convenient to

write the solution vectors k

( j)

= k

+ γ

( j)

n. (5.48)

This expression guarantees that all wave vectors k

( j)

have the same component

normal to the vector n. Let us use this expression to rewrite equation (5.45):

−



( j)

+ g



= k

−



+ γ

( j)

n + g



;

=−g · (2k

+ g) − 2n · (k

+ g)γ

( j)

−



( j)



;

= 2k

− 2n · (k

+ g)γ

( j)

−



( j)



. (5.49)

We have used the deﬁnition (2.89) of the excitation error s

in the last step. At this

point, we will make the assumption that the coefﬁcients γ

( j)

are small compared

to k

, so that the quadratic term in γ

( j)

can be ignored. This is equivalent to the

high-energy approximation used in the previous sections, and as a result only N of

the 2N wave vectors k

( j)

remain.

‡

The N wave vectors which we chose to ignore

†

Note that some authors select the foil normal to point along the incident beam. The reader should be aware that

this leads to sign differences for the coefﬁcients γ

( j )

‡

Equation (5.49) is now linear instead of quadratic in γ

( j )

324 Dynamical electron scattering in perfect crystals

Ewald

sphere

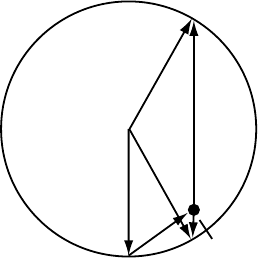
Fig. 5.3. Schematic illustration of positive and negative excitation errors for a single recip-

rocal lattice point. For large acceleration voltages, the negative excitation

error is always sig-

niﬁcantly larger than the positive one, justifying the use of the high-energy approximation.

correspond to electrons which travel in the direction opposite to the incident beam,

i.e. they correspond to reﬂected waves. For the acceleration voltages used in typical

TEM experiments this is a good approximation, as is shown explicitly in [KS82].

A simple geometrical argument can be used to qualitatively justify the high-

energy approximation. Consider the Ewald sphere construction in Fig. 5.3: the

reciprocal lattice point g is just inside the Ewald sphere, and if we assume that

the sample surfaces are normal to the incident beam k

(i.e. the corresponding

relrod is parallel to k

), then relation (2.89) on page 122 has two solutions for the

excitation error s

. The positive solution is small in magnitude and corresponds to

the excitation error used in the previous sections. The negative solution has a large

magnitude and corresponds to a beam traveling in nearly the opposite direction, i.e.

a reﬂected beam. The two scattered wave vectors are given by

= k

+ g + s

;

−

= k

+ g + s

−

The excitation error s

−

will increase rapidly with increasing acceleration voltage

(i.e. with increasing Ewald sphere radius), so that the probability of Bragg scattering

in the direction k

−

will decrease with decreasing wavelength. For the acceleration

voltages used in modern microscopes, it is a good approximation to consider only

electrons which were scattered in the forward direction (remember that the angle

between k

and k

is of the order of milliradians), and this is essentially the high-

energy approximation.

Elimination of half of the allowed wave vectors decreases the total number of

unknowns from 2N

+ 4N to N

+ 2N . If we denote the normal components of

5.7 Bloch wave description 325

and g by n · g = g

and n · k

= k

, then we ﬁnd for equations (5.45):

( j)



h=g

g−h

( j)

= 2k



1 +



( j)

. (5.50)

If k

is very nearly antiparallel to n, then we also have g

 k

and the equations

reduce to

( j)



h=g

g−h

( j)

= 2k

( j)

. (5.51)

These equations will serve as the starting point for the remainder of this section. It

is easy to see that (5.51) is an eigenvalue equation of the form

( j)

= 2k

( j)

, (5.52)

where the column vectors C

( j)

contain the Bloch wave coefﬁcients C

( j)

. For the

N -beam case, the matrix

A has N × N entries, and therefore N eigenvalues and N

eigenvectors. Solution of this equation will determine all wave vectors k

( j)

and all

Bloch wave coefﬁcients C

( j)

. The Bloch wave excitation amplitudes α

( j)

can then be

determined by applying the appropriate boundary conditions at the entrance plane,

as will be shown below. Since there are N eigenvalues, and N

components of the

N eigenvectors, and we also determine the N coefﬁcients α

( j)

from the boundary

conditions, we have effectively determined all N

+ 2N unknowns, and therefore

the problem is, at least formally, solved.

It is important to consider some general properties of the eigenvalues and eigen-

vectors of

A. For a non-centrosymmetric crystal we have U

= U

∗

−g

, and therefore

A is a hermitian matrix in the absence of absorption. The diagonal of

A contains

information about the orientation of the crystal, through the excitation errors s

and the off-diagonal elements contain information on the interactions between the

beams. The eigenvalues of a hermitian matrix are real, the eigenvectors are complex

and form a unitary matrix. In other words, when we consider the eigenvectors C

( j)

as columns of a matrix C, then this matrix satisﬁes the relation:

−1

∗

, (5.53)

where the tilde indicates the transposition operator. If we consider the equation

−1

= 1, with 1 the N × N unit matrix, then we can easily show that



(i)

( j)∗

= δ

, (5.54)

and



( j)

( j)∗

= δ

. (5.55)

326 Dynamical electron scattering in perfect crystals

This means that the eigenvectors of

A form an orthonormal set. Standard matrix

theory then states that

A can be written as

A = C

C, (5.56)

where is a diagonal matrix containing the eigenvalues. This decomposition of

is known as the spectral factorization of

5.7.2 Determination of the Bloch wave excitation coefﬁcients

The Bloch wave excitation coefﬁcients α

( j)

can be determined from the boundary

conditions at the crystal entrance plane. We will rewrite the Bloch wave expansion

in the so-called Darwin representation; this is essentially the expansion (5.7), which

formed the starting point for the derivation

of the Darwin

–Howie–Whelan equations

on page 306.

Using (5.48) we have

(r) =



( j)

2πiγ

( j )

2πi(k

+g)·r

;



(z)e

2πi(k

+g)·r

with

(z) =



( j)

2πiγ

( j )

. (5.57)

This can be rewritten in matrix form as







(z)













(1)

(2)

... C

(N )

(1)

(2)

... C

(N )

(1)

(2)

... C

(N )













2πiγ

(1)

0 ... 0

2πiγ

(2)

... 0

00... e

2πiγ

(N )













(1)

(2)

(N )







. (5.58)

5.7 Bloch wave description 327

At the entrance plane of the crystal we have z = 0, and the diagonal matrix reduces

to the identity matrix. The resulting equation is







(0)













(1)

(2)

... C

(N )

(1)

(2)

... C

(N )

(1)

(2)

... C

(N )













(1)

(2)

(N )



















. (5.59)

This, in turn, means that the Bloch wave excitation coefﬁcients α

( j)

are given by the

ﬁrst column of the inverse of the eigenvector matrix. In the case of a centrosymmetric

crystal without absorption, this matrix is Hermitian, which means (using 5.53) that

( j)

= C

( j)∗

Note that this derivation also produces an explicit expression for the scattering

matrix S, introduced on page 312. If we denote the diagonal matrix e

2πiγ

( j )

E(z), then we have

(z) = CE(z)C

−1

(0) = S(0). (5.60)

The Bloch wave formalism thus enables us to compute the scattering matrix directly

for an arbitrary crystal thickness. Only the diagonal matrix E(z) depends on the

crystal thickness, in a simple exponential way. Later we will see that this results

in a fast algorithm to compute bright ﬁeld and dark ﬁeld images, in particular for

the N -beam case. It is clear from the relations in this and the previous section that

the Bloch wave problem is completely solved if the spectral factorization (5.56) of

A is known. From the eigenvalues γ

( j)

and the eigenvector matrix C we can then

also compute the scattering matrix S. We will discuss an algorithm for spectral

factorization in Chapter 7.

5.7.3 Absorption in the Bloch wave formalism

Absorption is taken into account by adding an imaginary part to the electrostatic

lattice potential. The eigenvalues γ

( j)

then become complex, and we will denote

the new eigenvalues by !

( j)

= γ

( j)

+ iq

( j)

. Consequently, the wave vectors inside

the crystal are given by

( j)

= k



( j)

+ iq

( j)

