Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 221

using discrete probability distributions

So do linear transforms give me a quick way

of calculating the expectation and variance

when I want to play multiple games?

There’s a difference between using linear transforms and

playing multiple games.

With linear transforms, all of the probabilities stay the same, but the possible values

change. The values are transformed, but not the probabilities. There are still the same

number of possible values.

When you play multiple games, both the values and the probabilities are different,

and even the number of possible values can change. It’s not possible to just transform

the values, and working out the probabilities can quickly become complicated.

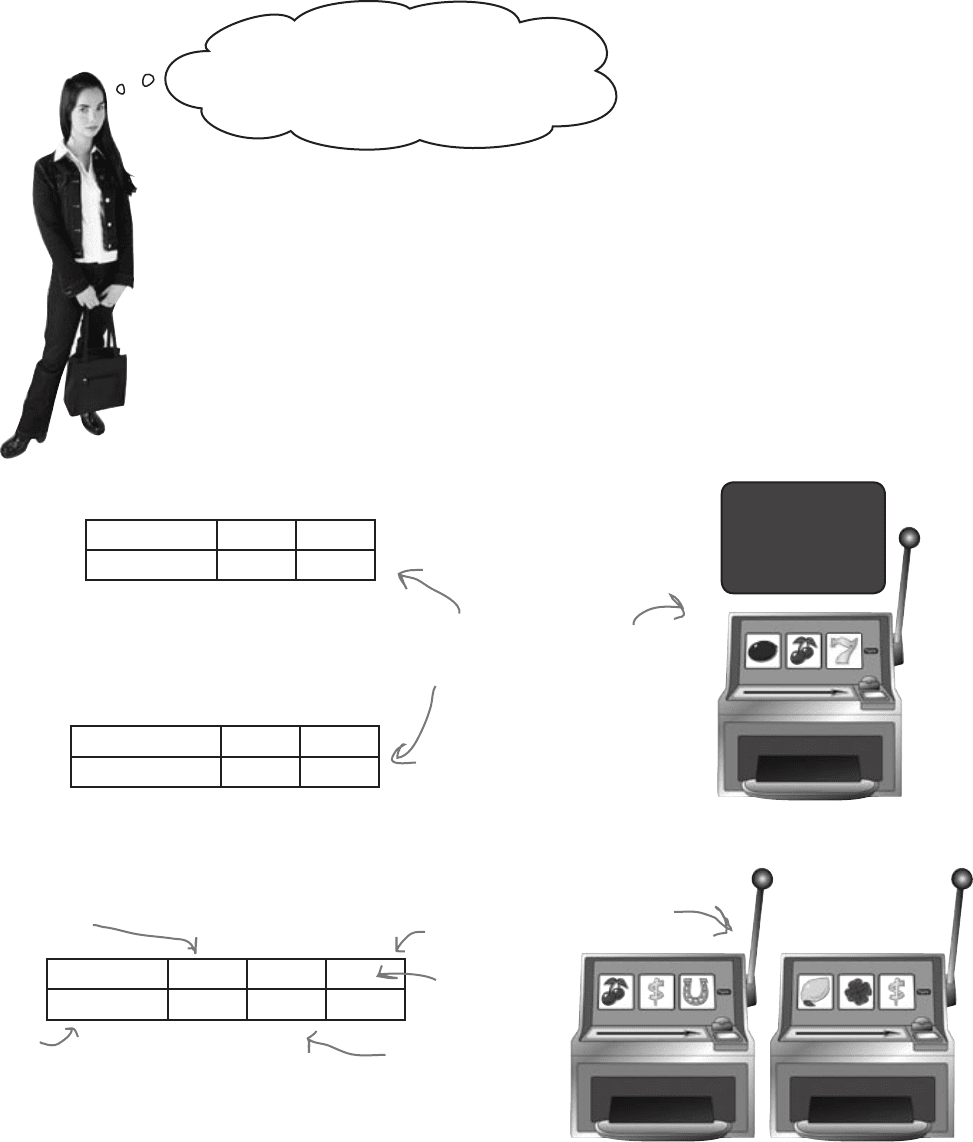
Let’s look at a simple example. Imagine you were playing on a very simple slot

machine with probability distribution X.

What if you were going to play two games on

the slot machine? You’d need to work out the

probability distribution from scratch by considering

all the possible outcomes from both games.

The amounts here are

multiplied by 2. The

probabilities stay the same

as before.

To find the probability distribution of 2X, you just need

to multiply the x values by 2. The underlying values

change because the potential gains have doubled.

x -1 5

P(X = x)

0.9 0.1

2x -2 10

P(2X = 2x)

0.9 0.1

w -2 4 10

P(W = w)

0.81 0.18 0.01

This time, both the probabilities and values have

changed. So how can we find the expectation and

variance for this situation?

This is like pulling the handle

twice. The possible gains and

probabilities are different.

y=4 when you by

get -1 in one game

and 5 in the other.

Now pays

double!

y=-2 if you lose

both games.

y=10 if you

win both

games.

W represents

the outcome

of two games

222 Chapter 5

x -1 5

P(X = x)

0.9 0.1

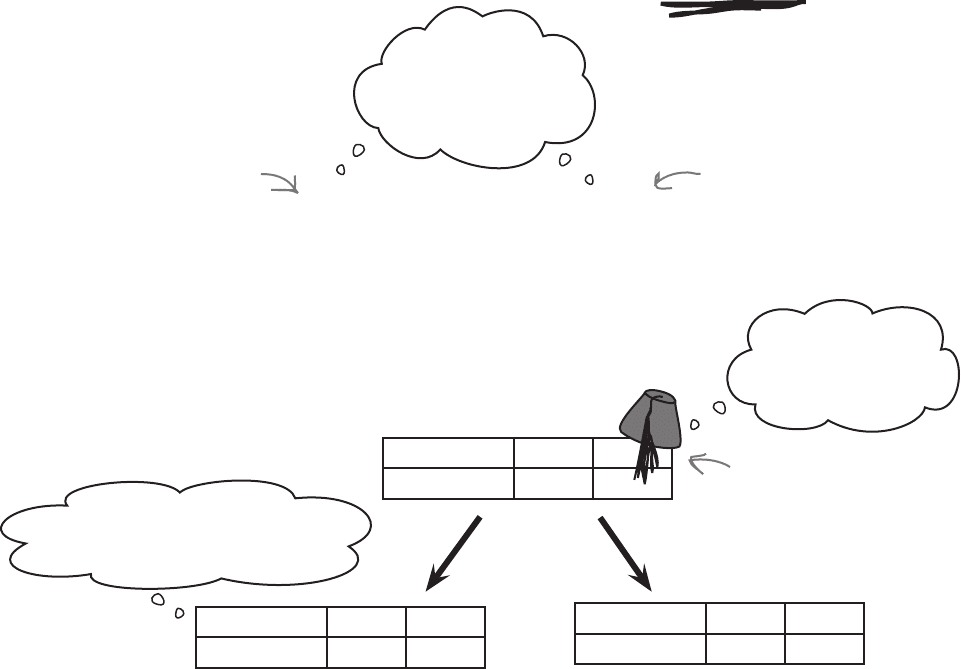
When we play multiple games on the slot machine, each game

is called an event, and the outcome of each game is called an

observation. Each observation has the same expectation and

variance, but their outcomes can be different. You may not gain

the same amount in each game.

We need some way of differentiating between the different

games or observations. If the probability distribution of the slot

machine gains is represented by X, we call the first observation

and the second observation X

Each game is called

an event.

The outcome of each

game is called an

observation.

We have the same

expectation and

variance, but we’re

separate events.

Observation for game 1

Observation for game 2

and X

have the same probabilities, possible values,

expectation and variance as X. In other words, they have the

same probability distribution, even though they are separate

observations and their outcomes can be different.

-1 5

P(X

= x

)

0.9 0.1

-1 5

P(X

= x

)

0.9 0.1

and X

base

themselves on me,

I’m their role model.

Grand Master probability

distribution X

When we want to find the expectation and variance of two

games on the slot machine, what we really want to find is

the expectation and variance of X

+ X

. Let’s take a look at

some shortcuts.

So that’s where we get our

probability distributions from.

Every pull of the lever is an independent observation

introducing independent observations

you are here 4 223

using discrete probability distributions

E(X

+ X

) = E(X

) + E(X

)

= E(X) + E(X)

= 2E(X)

Variance

So what about Var(X

+ X

)? Here’s the calculation.

Var(X

+ X

) = Var(X

) + Var(X

)

= Var(X) + Var(X)

= 2Var(X)

This means that if we were to play two games on a slot machine where

Var(X) = 2.6971, the variance would be 2.6971

2, or 5.3942.

We can extend this for any number of independent observations. If we

have n independent observations of X

Var(X

+ X

+ ... X

) = nVar(X)

Observation shortcuts

Let’s find the expectation and variance of X

+ X

E(X

) and E(X

) are both

equal to E(X) as X

and X

follow the same probability

distribution as X

In other words, if we have the expectation of two observations, we

multiply E(X) by 2. This means that if we were to play two games

on a slot machine where E(X) = -0.77, the expectation would be

-0.77

2, or -1.54.

We can extend this to deal with multiple observations. If we want to

find the expectation of n observations, we can use

E(X

+ X

+ ... X

) = nE(X)

If there are n observations,

we just multiply E(X) by n.

In other words, to find the expectation and variance of multiple

observations, just multiply E(X) and Var(X) by the number of observations.

Multiply Var(X) by n, the

number of observations.

Var(X

) and Var(X

) are the same as Var(X) as X

and X

follow the same probability distribution as X.

Expectation

First of all, let’s deal with E(X

+ X

is not

the same as 2X.

+ X

means you

are considering

two observations

of X. 2X means you have one

observation, but the possible

values have doubled.

224 Chapter 5

Isn’t E(X

+ X

) the same as E(2X)?

A: They look similar but they’re actually

two different concepts.

With E(2X), you want to find the expectation

of a variable where the underlying values

have been doubled. In other words, there’s

only one variable, but the values are twice

the size.

With E(X

+ X

), you’re looking at two

separate instances of X, and you’re looking

at the joint expectation. As an example, if X

represents the distribution of a game, then

+ X

represents the distribution of two

games.

So are X

and X

the same?

A: They follow the same distribution, but

they’re different instances or observations.

As an example, X

could refer to game

1, and X

to game 2. They both have the

same probability distribution, but the actual

outcome of each might be different.

I see that the new variance is

nVar(X) and not n

Var(X) like we had for

linear transforms. Why’s that?

A: This time we have a series of

independent observations, all distributed the

same way. This means that we can find the

overall variance by adding the variance of

each one together. If we have n independent

observations, then this gives us nVar(X).

When we calculate the variance of Var(nX),

we multiply the underlying values by n. As

the variance is formed by squaring the

underlying values, this means that the

resulting variance is n

Var(X).

Probability distributions describe the probability of

all possible outcomes of a given random variable.

The expectation of a random variable X is the

expected long-term average. It’s represented as

either E(X) or μ. It’s calculated using

E(X) = xP(X=x)

The variance of a random variable X is given by

Var(X) = E(X - μ)



The standard deviation σ is the square root of the

variance.

Linear transforms are when a random variable

X is transformed into aX + b, where a and b are

numbers. The expectation and variance are given

E(aX + b) = aE(X) + b

Var(aX + b) = a

Var(X)



no dumb questions

Independent Observations

Use the following formula to calculate the

variance

E(X

+ X

+ ... + X

) = nE(X)

Var(X

+ X

+ ... + X

) = nVar(X)

Vital StatisticsVital Statistics

you are here 4 225

using discrete probability distributions

The amount of coffee in an extra

large cup of coffee; X is the amount

of coffee in a normal-sized cup.

Below are a series of scenarios. Assuming you know the distribution

of each X, and your task is to say whether you can solve each problem

using linear transforms or independent observations.

Linear

transform

Independent

observation

Finding the net gain from a lottery

ticket after the price of tickets

goes up; X is the net gain of buying

1 lottery ticket.

Drinking an extra cup of coffee

per day; X is the amount of coffee

in a cup.

Finding the net gain from buying 10

lottery tickets; X is the net gain of

buying 1 lottery ticket.

Buying an extra hen to lay eggs

for breakfast; X is the number of

eggs laid per week by a certain

breed of hen.

Linear Transform

or Independent

Observation?

226 Chapter 5

The amount of coffee in an extra

large cup of coffee; X is the amount

of coffee in a normal-sized cup.

Below are a series of scenarios. Assuming you know the distribution

of each X, and your task is to say whether you can solve each problem

using linear transforms or independent observations.

Linear

transform

Independent

observation

Finding the net gain from a lottery

ticket after the price of tickets

goes up; X is the net gain of buying

1 lottery ticket.

Drinking an extra cup of coffee

per day; X is the amount of coffee

in a cup.

Finding the net gain from buying 10

lottery tickets; X is the net gain of

buying 1 lottery ticket.

Buying an extra hen to lay eggs

for breakfast; X is the number of

eggs laid per week by a certain

breed of hen.

Linear Transform

or Independent

Observation?

Solution

The winnings from each

lottery ticket are

independent of the others.

Changing the price of a ticket

changes the expected winnings, but

not the probability of winning,

so this can be solved with linear

transforms.

linear transform or independent observation solution

you are here 4 227

using discrete probability distributions

The local diner has started selling fortune cookies at $0.50 per cookie. Hidden within

each cookie is a secret message. Most messages predict a good future for the buyer,

but others offer money off at the diner. The probability of getting $2 off is 0.1, the

probability of getting $5 off is 0.07, and the probability of getting $10 off is 0.03.

If X is the net gain, what’s the probability distribution of X? What are the values of E(X)

and Var(X)?

The diner decides to put the price of the cookies up to $1. What are the new expectation and variance?

228 Chapter 5

The local diner has started selling fortune cookies at $0.50 per cookie. Hidden within

each cookie is a secret message. Most messages predict a good future for the buyer,

but others offer money off at the diner. The probability of getting $2 off is 0.1, the

probability of getting $5 off is 0.07, and the probability of getting $10 off is 0.03.

If X is the net gain, what’s the probability distribution of X? What are the values of E(X)

and Var(X)?

x -0.5 1.5 4.5 9.5

P(X = x) 0.8 0.1 0.07 0.03

Here’s the probability distribution of X:

E(X) = (-0.5)x0.8 + 1.5x0.1 + 4.5x0.07 + 9.5x0.03

= -0.4 + 0.15 + 0.315 + 0.285

= 0.35

Var(X) = E(X - μ)

= (x - μ)

P(X=x)

= (-0.5-0.35)

x0.8 + (1.5-0.35)

x0.1 + (4.5-0.35)

x0.07 + (9.5-0.35)

x0.03

= (-0.85)

x0.8 + (1.15)

x0.1 + (4.15)

x0.07 + (9.15)

x0.03

= 0.7225x0.8 + 1.3225x0.1 + 17.2225x0.07 + 83.7225x0.03

= 0.578 + 0.13225 + 1.205575 + 2.511675

= 4.4275

The diner decides to put the price of the cookies up to $1. What are the new expectation and variance?

The diner puts the price of the cookies up by $0.50, which means that

the new net gains are modelled by X - 0.5

E(X - 0.5) = E(X) - 0.5

= 0.35 - 0.5

= -0.15

Var(X - 0.5) = Var(X)

= 4.4275

exercise solution

you are here 4 229

using discrete probability distributions

New slot machine on the block

Fat Dan has brought in a new model slot machine. Each

game costs more, but if you win you’ll win big. Here’s the

probability distribution:

x -5 395

P(X = x)

0.99 0.01

Each game costs more

than the other slot

machine, but just look

at the jackpot!

We’ve looked at the expectation and variance of playing a

single machine, and also for playing several independent games

on the same machine. What happens if we play two different

machines at once?

In this situation, we have two different, independent probability

distributions for our machines:

y -2 23 48 73 98

P(Y = y)

0.977 0.008 0.008 0.006 0.001

These are the

current gains of our

original slot machine.

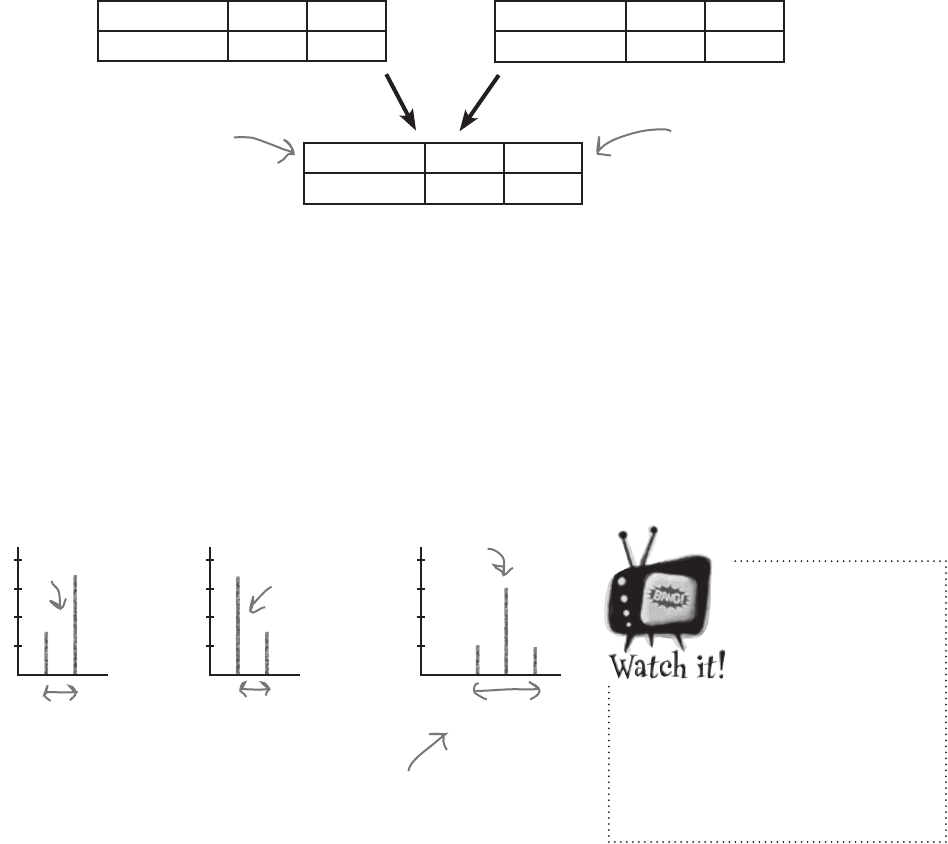
So how can we find the expectation and variance of playing

one game each on both machines?

We could work out the probability

distribution of X + Y, but that would be time-

consuming, and we might make a mistake. I

wonder if we can take another shortcut?

New!

x -5 395

P(X = x)

0.99 0.01

These are the current

gains of Fat Dan’s new

slot machine.

230 Chapter 5

Add E(X) and E(Y) to get E(X + Y)…

We want to find the expectation and variance of playing one game each

on both of the slot machines. In other words, we want to find E(X + Y)

and Var(X + Y) where X and Y are random variables representing the

two machines. X and Y are independent.

One way of doing this would be to calculate the probability distribution

of X + Y, and then calculate the expectation and variance.

x + y

Can you imagine how long

it would take us to work

this out, and how many

mistakes we’d make?

Fortunately we don’t have to do this. To find E(X + Y), all we

need to do is add together E(X) and E(Y).

Intuitively this makes sense. If, for example, you were playing

two games where you would expect to win $5 in one game

and $10 in the other, you would expect to win $15 overall—

$5 + $10.

We can do something similar with the variance. To find

Var(X +Y), we add the two variances together. This works for

all independent random variables.

E(X + Y) = E(X) + E(Y)

Var(X + Y) = Var(X) + Var(Y)

Adding the

variances

together only

works for

independent

random variables

If X and Y are not independent,

then Var(X + Y) is no longer

equal to Var(X) + Var(Y).

E(X)

E(Y)

E(X + Y)

Var(X)

Var(Y)

Var(X + Y)

The variance increases—the

probability distribution

varies more.

0 0 0

Don’t worry, we’re not asking

you to calculate this.

addition and subtraction of random variables