Griffiths D. Head First Statistics

Подождите немного. Документ загружается.

you are here 4 191

calculating probabilities

It’s great that we know our chances

of winning all these different bets, but

don’t we need to know more than just

probability to make smart bets?

Winner! Winner!

On both spins of the wheel, the ball landed on 30, a red

square, and you doubled your winnings.

You’ve learned a lot about probability over at Fat Dan’s

roulette table, and you’ll find this knowledge will come in

handy for what’s ahead at the casino. It’s a pity you didn’t

win enough chips to take any home with you, though.

Besides the chances of winning, you

also need to know how much you

stand to win in order to decide if the

bet is worth the risk.

Betting on an event that has a very low probability

may be worth it if the payoff is high enough to

compensate you for the risk. In the next chapter,

we’ll look at how to factor these payoffs into our

probability calculations to help us make more

informed betting decisions.

[Note from Fat Dan:

That’s a relief.]

192 Chapter 4

The Absent-Minded Diners

Three absent-minded friends decide to go out for a meal, but

they forget where they’re going to meet. Fred decides to throw a

coin. If it lands heads, he’ll go to the diner; tails, and he’ll go to the

Italian restaurant. George throws a coin, too; heads, it’s the Italian

restaurant; tails, it’s the diner. Ron decides he’ll just go to the

Italian restaurant because he likes the food.

What’s the probability all three friends meet? What’s the

probability one of them eats alone?

probability puzzle

you are here 4 193

calculating probabilities

Here are some more roulette probabilities for you to work out.

1. The probability of the ball having landed on the number 17 given the pocket is black.

2. The probability of the ball landing on pocket number 22 twice in a row.

3. The probability of the ball having landed in a pocket with a number greater than 4 given that

it’s red.

4. The probability of the ball landing in pockets 1, 2, 3, or 4.

194 Chapter 4

Diner

Italian

Diner

Italian

Ron

George

Fred

0.5

If all friends meet, it must be at the Italian

restaurant. We need to find

P(Ron Italian

∩ Fred Italian ∩ George Italian)

= 1 x 0.5 x 0.5 = 0.25

1 person eats alone if Fred and George go to the Diner.

Fred goes to the Diner while George goes to Italian

restaurant, or George goes to the Diner and Fred gets

Italian..

(0.5 x 0.5) + (0.5 x 0.5) + (0.5 x 0.5) = 0.75

Three absent-minded friends decide to go out for a meal, but

they forget where they’re going to meet. Fred decides to throw a

coin. If it lands heads, he’ll go to the diner; tails, and he’ll go to the

Italian restaurant. George throws a coin, too; heads, it’s the Italian

restaurant; tails, it’s the diner. Ron decides he’ll just go to the

Italian restaurant because he likes the food.

What’s the probability all three friends meet? What’s the

probability one of them eats alone?

The Absent-Minded Diners solution

puzzle solution

you are here 4 195

calculating probabilities

Here are some more roulette probabilities for you to work out.

1. The probability of the ball having landed on the number 17 given the pocket is black.

2. The probability of the ball landing on pocket number 22 twice in a row.

3. The probability of the ball having landed in a pocket with a number greater than 4 given that

it’s red.

4. The probability of the ball landing in pockets 1, 2, 3, or 4.

There are 18 black pockets, and one of them is numbered 17.

P(17 | Black) = 1/18 = 0.0556 (to 3 decimal places)

We need to find P(22

∩ 22). As these events are independent, this is

equal to P(22) x P(22). The probability of getting a 22 is 1/38, so

P(22

∩ 22) = 1/38 x 1/38 = 1/1444 = 0.00069 (to 5 decimal places)

P(Above 4 | Red) = 1 - P(4 or below | Red)

There are 2 red numbers below 4, so this gives us

1 - (1/18 + 1/18) = 8/9 = 0.889 (to 3 decimal places)

The probability of each pocket is 1/38, so the probability of this event

is 4 x 1/38 = 4/38 = 0.105 (to 3 decimal places)

this is a new chapter 197

OK, so falling out the tree was

unexpected, but you have to take

a long-term view of these things.

using discrete probability distributions

Manage Your Expectations

Unlikely events happen, but what are the consequences?

So far we’ve looked at how probabilities tell you how likely certain events are. What

probability doesn’t tell you is the overall impact of these events, and what it means

to you. Sure, you’ll sometimes make it big on the roulette table, but is it really worth it

with all the money you lose in the meantime? In this chapter, we’ll show you how you

can use probability to predict long-term outcomes, and also measure the certainty

of these predictions.

198 Chapter 5

$1 for each game

= $20

(any order) = $15

= $10

= $5

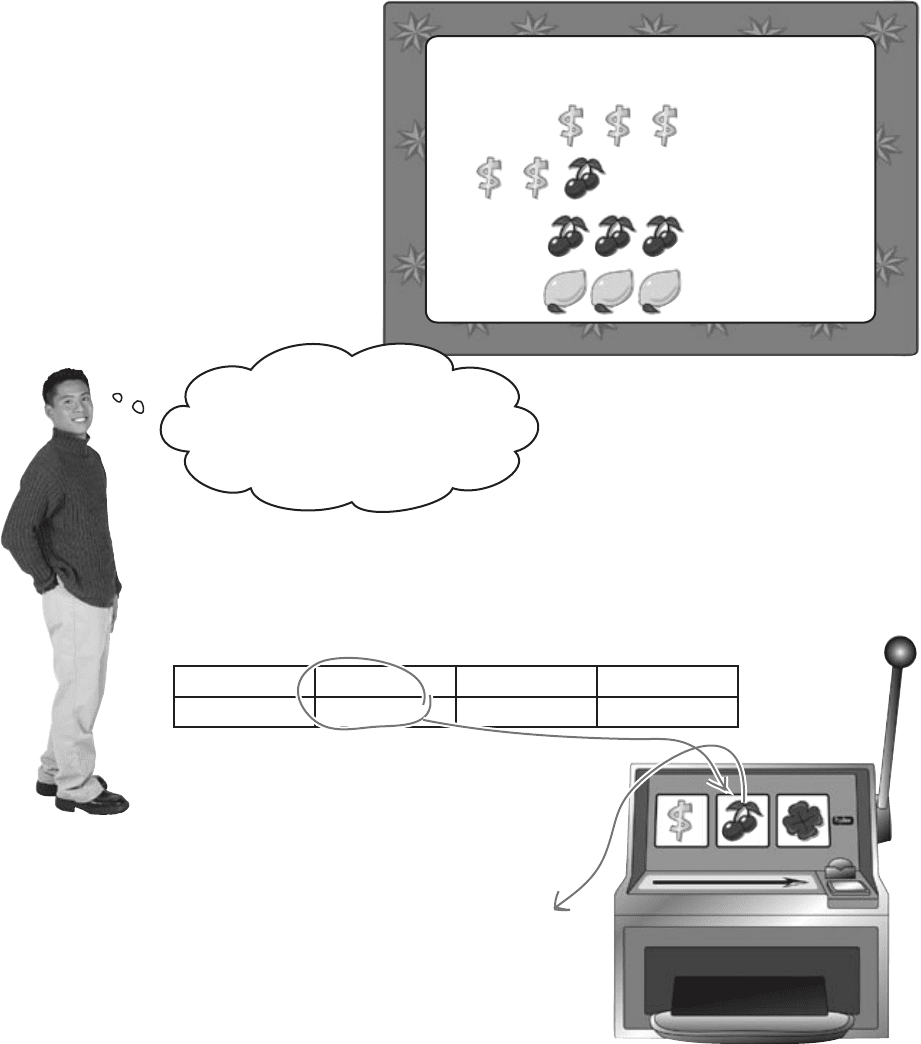
Back at Fat Dan’s Casino

Have you ever felt mesmerized by the

flashing lights of a slot machine? Well,

you’re in luck. At Fat Dan’s Casino, there’s

a full row of shiny slot machines just waiting

to be played. Let’s play one of them, which

costs $1 per game (pull of the lever). Who

knows, maybe you’ll hit jackpot!

The slot machine has three windows, and

if all three windows line up in the right way,

the cash will come cascading out.

The amount of money

you can win looks tempting, but

I’d like to know the probability of

getting any of these combinations

before playing.

This sounds like something we can calculate.

Here are the probabilities of a particular image

appearing in a particular window:

$ Cherry Lemon Other

0.1 0.2 0.2 0.5

The three windows are independent of each other,

which means that the image that appears in one of

the windows has no effect on the images that appear

in any of the others.

The probability of a cherry

appearing in this window is

0.2.

slot machine payouts

you are here 4 199

using discrete probability distributions

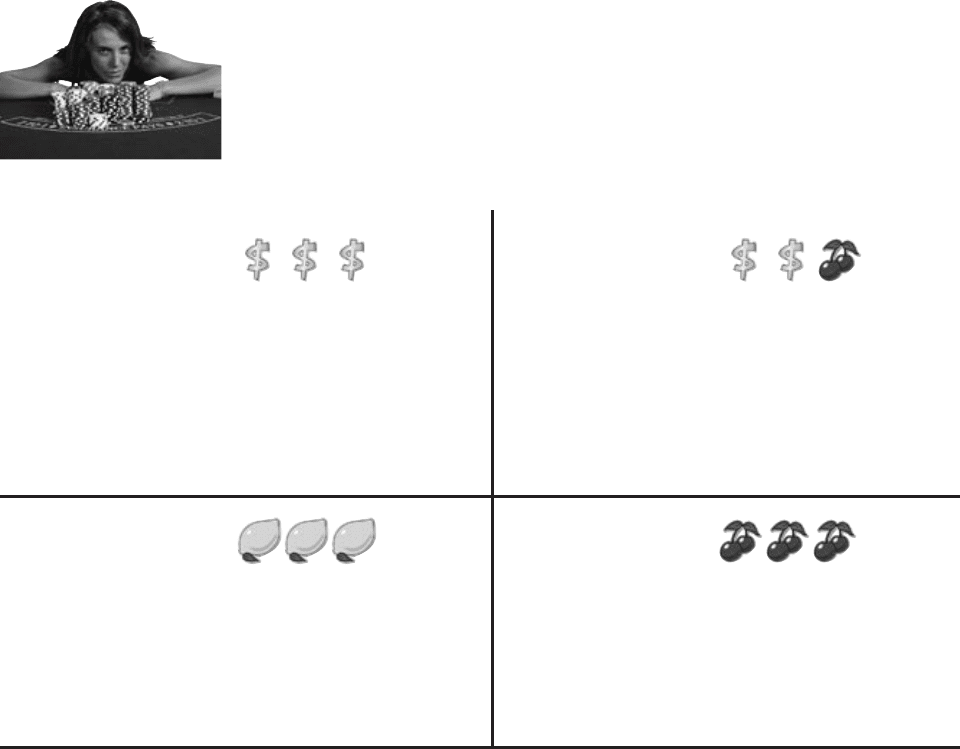
BE the gambler

Take a look at the poster for the slot machine on the

facing page. Your job is to play like you’re the

gambler and work out the probability of getting

each combination on the poster. What’s the

probability of not winning anything?

probability of winning nothing

probability of probability of

(any order)

200 Chapter 5

P($, $, $) = P($) x P($) x P($)

= 0.1 x 0.1 x 0.1

= 0.001

There are three ways of getting this:

P($, $, cherry) + P($, cherry, $) + P(cherry, $, $)

= (0.1

x 0.2) + (0.1

x 0.2)

= 0.006

P(cherry, cherry, cherry) = P(cherry) x P(cherry) x P(cherry)

= 0.2 x 0.2 x 0.2

= 0.008

P(lemon, lemon, lemon) = P(lemon) x P(lemon) x P(lemon)

= 0.2 x 0.2 x 0.2

= 0.008

This means we get none of the winning combinations.

P(losing) = 1 - P($, $, $) - P($, $, cherry (any order)) - P(cherry, cherry, cherry) - P(lemon, lemon, lemon)

= 1 - 0.001 - 0.006 - 0.008 - 0.008

= 0.977

Rather than work out all the possible ways in which

you could lose, you can say P(losing) = 1 - P(winning).

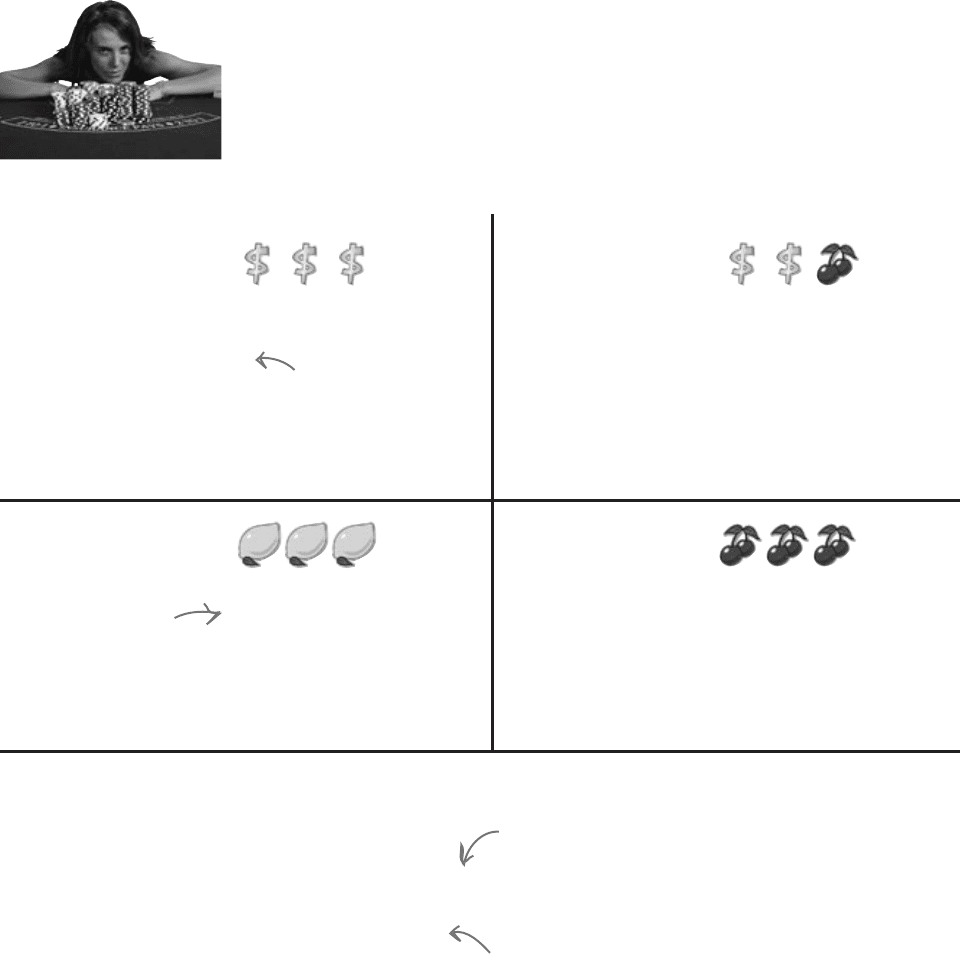
probability of winning nothing

probability of probability of

(any order)

These are the four probability values we

calculated above.

The probability of a

dollar sign appearing in

a window is 0.1

A lemon appearing in a window

is independent of ones

appearing in the other two

windows, so you multiply the

three probabilities together.

BE the gambler solution

Take a look at the poster for the slot machine on the

facing page. Your job is to play like you’re the

gambler and work out the probability of getting

each combination on the poster. What’s the

probability of not winning anything?

be the gambler solution