Gubbins D., Herrero-Bervera E. Encyclopedia of Geomagnetism and Paleomagnetism

Подождите немного. Документ загружается.

evidence of external forcing that is independent of climatological var-

iations. Spectral analysis of the relative paleointensity record from

ocean sediments (Channell et al., 1997) show modulation of intensity

corresponding to orbital obliquity and eccentricity periods. The incli-

nation error found in a 2 Ma long record from the west Caroline basin

(Yamazaki and Oda, 2002) correlates to orbital eccentricity.

Although gravitational energy released through compositional con-

vection is considered to drive the core’s geodynamo that maintains

the geomagnetic field, other phenomena like rotational parametric

instabilities may prove to play a significant role in maintaining the

geodynamo.

Keith Aldridge

Bibliography

Aldridge, K.D., 2003. Dynamics of the core at short periods: theory,

experiments and observations. In Jones, C.A., Soward, A.M., and

Zhang, K. (eds.), Earth’s Core and Lower Mantle, The Fluid

Mechanics of Astrophysics and Geophysics. London: Taylor &

Francis.

Aldridge, K.D., and Baker, R.E., 2003. Paleomagnetic intensity data: a

window on the dynamics of Earth’s fluid core? Physics of the

Earth and Planetary Interiors, 140:91–100.

Aldridge, K.D., and Cannon, W.H., 1993. A search for evidence

of short period polar motion in VLBI and supergravimetry

observations. Proceedings of the IUGG XX Assembly, Symposium

U6: Dynamics of the Earth’s Deep Interior and Earth Rotation,

American Geophysical Union Geophysical Monograph 72,

pp. 17–24.

Aldridge, K.D., and Toomre, A., 1969. Axisymmetric inertial oscilla-

tions of a fluid in a rotating spherical container. Journal of Fluid

Mechanics, 37: 307–323.

Aldridge, K.D., Lumb, L.I., and Henderson, G., 1988. Inertial modes

in the Earth’s fluid outer core. Proceedings of the International

Union of Geodesy and Geophysics XIX Assembly, Symposium

U2: Instability within the Earth and core dynamics, American

Geophysical Union Monograph 46, pp. 13– 21.

Channell, J.E.T., Hodell, D.A., and Lehman, B., 1997. Relative geo-

magnetic paleointensity and d

O at ODP Site 983 (Garder Drift,

North Atlantic) since 350 ka. Earth and Planetary Science Letters,

153: 103–118.

Crossley, D., Hinderer, J., and Legros, H., 1991. On the excitation,

detection and damping of core modes. Physics of the Earth and

Planetary Interiors, 116:68–97.

Dintrans, B., Rieutord, M., and Valdettaro, L., 1999. Gravito-inertial

waves in a rotating stratified spherical shell. Journal of Fluid

Mechanics, 398: 271–297.

Greenspan, H., 1969. The Theory of Rotating Fluids. Cambridge:

Cambridge University Press.

Hollerbach, R., and Kerswell, R.R., 1995. Oscillatory internal shear

layers in rotating and precessing flows. Journal of Fluid Mechanics,

298: 327–339.

Kent, D.V., and Opdyke, N., 1977. Paleomagnetic field intensity varia-

tions recorded in a Brunhes epoch deep-sea sediment core. Nature,

266: 156–159.

Kerswell, R.R., 1993. The instability of precessing flow. Geophysical

and Astrophysical Fluid Dynamics, 72: 107–114.

Kerswell, R.R., 2002. Elliptical instability. Annual Review of Fluid

Mechanics, 34:83–113.

Noir, J., Brito, D., Aldridge, K., and Cardin, P., 2001. Experimental

evidence of inertial waves in a precessing spheroidal cavity. Geo-

physical Research Letters, 19: 3785–3788.

Rieutord, M., Georgeot, B., and Valdettaro, L., 2001. Inertial waves

in a rotating spherical shell: attractors and asymptotic spectrum.

Journal of Fluid Mechanics, 435: 103–144.

Tilgner, A., 1999. Driven inertial oscillations in spherical shells.

Physical Review E, 59: 1789–1794.

Yamazaki, T., and Oda, H., 2002. Orbital influence on Earth’s

magnetic field: 100000 year periodicity in inclination. Science,

295: 2435–2438.

Zhang, K., Earnshaw, P., Liao, X., and Busse, F.H., 2001. On inertial

waves in a rotating fluid sphere. Journal of Fluid Mechanics,

437: 103

–119.

Cross-references

Core Density

Core Turbulence

Core, Adiabatic Gradient

Core, Boundary Layers

Fluid Dynamics Experiments

Helioseismology

Paleointensity, Relative, in Sediments

Precession and Core Dynamics

GRU

NEISEN’S PARAMETER FOR IRON AND

EARTH’S CORE

Introduction

The Grüneisen parameter g is a necessary tool for assessing Earth’s

thermal properties. Here we emphasize aspects of g that are pertinent

to Earth’s core. g has various definitions, many of which are derivable

one from another by thermodynamic identities. The following equation

for g quantifies the relationship between the thermal and elastic proper-

ties of a solid. The parameter g can be considered as a measure of the

change in pressure P resulting from an increase in energy density at

constant volume V. It is dimensionless, since pressure and DU=V have

the same units

g ¼ V



(Eq. 1)

where U is the internal energy. From Eq. (1) it is seen that g connects

pressure and energy, and therefore, pressure and temperature. Elasti-

city properties of Earth’s core (especially pressure) come

from seismological data. Gamma is useful to obtain energy and tem-

perature from these seismological data. Another example of the impor-

tance of g is in the expression used for thermal pressure at high

temperature

(Eq. 2)

the so-called Mie-Grüneisen relationship (E

is the thermal energy

and P

is the thermal pressure). This equation is often used with an

isothermal equation of state, P(V,T

). Equation (1) is the general state-

ment of the relationship between pressure and energy of which Eq. (2)

is a special case. Equation (2) can be considered as the historical

presentation of g, attributed to Grüneisen (1926), who derived the

equation for pressure as a function of volume and temperature in an

early version of lattice dynamics.

For many physical properties of the Earth’s interior, we need to know

the value of g of a solid at the pressure and temperature of the Earth’s

interior, not just at ambient conditions. We need to know how g changes

with T, especially at high T, if at all, and how g changes with pressure

(or rather, volume), especially at high compression.

366 GRU

NEISEN’S PARAMETER FOR IRON AND EARTH’S CORE

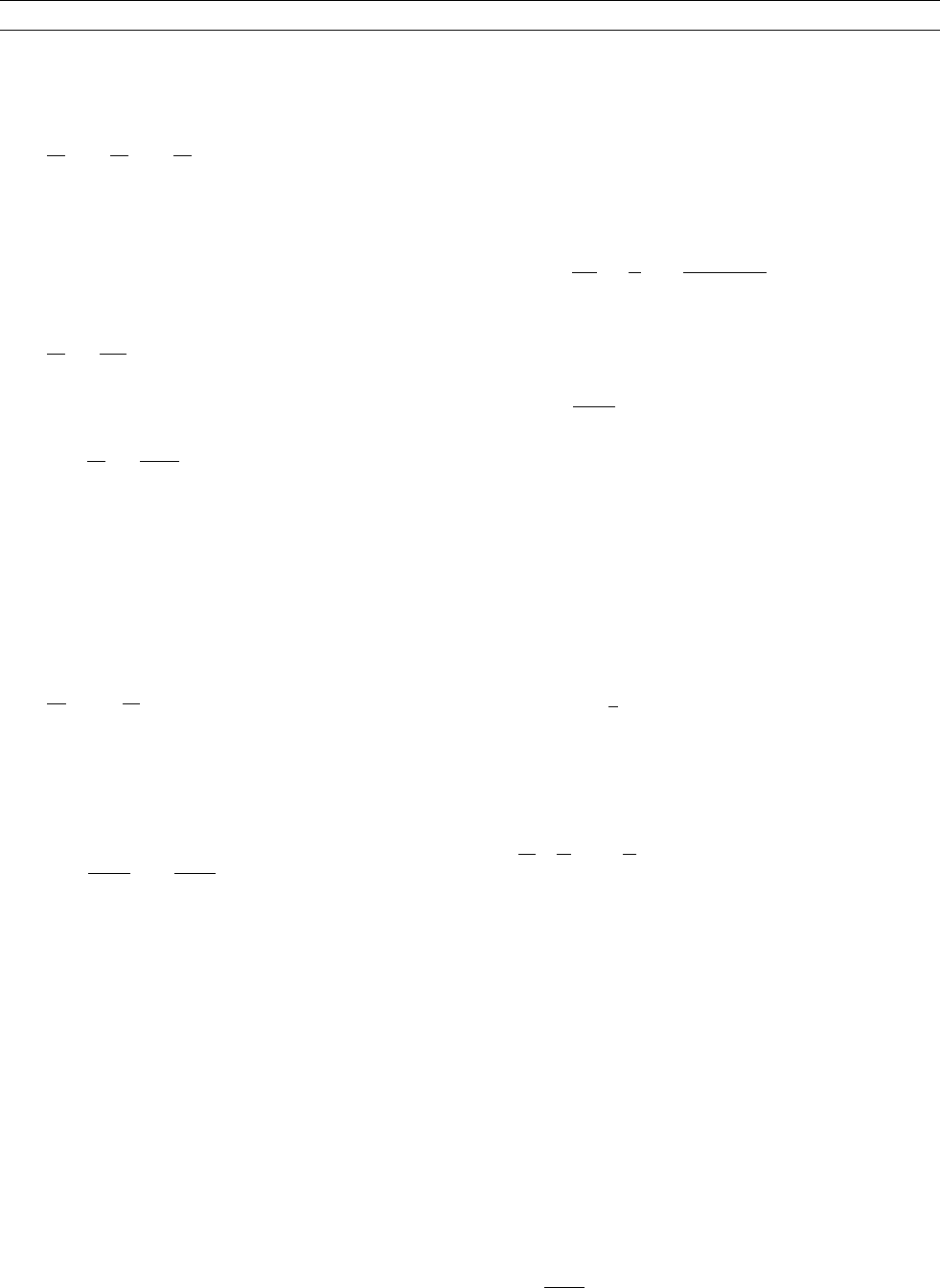
Thermodynamic derivations of gamma

In order to evaluate Eq. (1) in parameters representing measurable

physical properties, start with the following equation







(Eq. 3)

The definition of specific heat is ð]U=]TÞ

¼ C

at unit mass

(all quantities are per unit mass). The numerator on the

right side of Eq. (3) is found from calculus: ð]P=]TÞ

ð]V=]TÞ

=ð]V=]PÞ

¼ aK

, where a is the volume thermal expan-

sivity, and K

is the isothermal bulk modulus. Equation (3) is therefore

equivalent to



(Eq. 4)

Using Eq. (4) in Eq. (1), the most useful definition of g is found:

g ¼ V



(Eq. 5)

g as given by Eq. (5) is composed of individual measurable physical

properties, each of which varies significantly with temperature. The

ratio of these properties as given by Eq. (5), however, does not vary

greatly with temperature, and often not at all. There are many approx-

imations to Eq. (5) for g. The few approximations we will use here will

be given special subscripts and names.

Another method of finding g involves adiabatic compression. Start

with one of Maxwell’s relationships:



¼



(Eq. 6)

Expand the right side of Eq. (6): ð]P=]SÞ

¼ð]P=]TÞ

ð]T=]SÞ

By using ð ] P=]TÞ

¼ aK

and ð]S=]TÞ

¼ C

, the right side of this

equation becomes TaK

. Using Eq. (5), the right side becomes

Tg=V, so that Eq. (6) can also be written as

g ¼

] ln T

] ln V



] ln T

] ln r



(Eq. 7)

Equation (7) is the thermodynamic basis for finding the adiabatic ther-

mal gradient in the core and mantle.

Equations (1), (2), (5), and (7) are thermodynamically equivalent

definitions of g. The choice of the equation to use depends on the para-

meters at hand and the result desired.

Lattice dynamic derivations of gamma

The lattice dynamic view of a solid is that of statistical mechanics:

a solid is composed of N atoms (where N is Avogadro’s number); each

atom is an oscillator having three degrees of freedom and connected to

neighboring atoms by a spring. The solid’s thermodynamic properties

are found from the dynamics of 3N vibrations with modal frequencies

, n

; ...; n

. Each modal vibration arises from a simple harmo-

nic oscillation, the energy of which is given by an Einstein function,

and the frequency of which is classically related to the atomic

mass and the spring constant. For a monatomic solid, such as iron,

all the masses are equal. A standard treatment of this subject shows

that the Helmholtz free energy for a monatomic solid of N degrees

of freedom is (Slater, 1939)

F¼U

kT ln 1  e

hn

=kT



(Eq. 8)

where k is Boltzmann’s constant and h is h=2p, where h itself is

Planck’s constant, and where the quantity under the summation sign

is the Einstein function.

The isothermal equation of state P(V ) is found by differentiating

Eq. (8) with respect to V at constant T, giving

P ¼



hn

=kT

 1



(Eq. 9)

Attention is directed to g

, called the mode gamma, which arises from

the V derivative

¼

] ln n

] ln V



(Eq. 10)

Although g

is dimensionless, its value is influenced by the rate of

change of mode frequency with volume. Thus, in order for g

to be

nonzero, it must change with volume, and for it to be positive, it must

decrease with volume. It is customary to make an assumption (called

the quasiharmonic assumption) that the mode gammas depend on

volume but are independent of temperature.

For core physics, where the temperature is high, the high-temperature

limit of the above equations is needed. The Debye temperature Y

marks the division between the high temperature region and the

quantum state region of a solid. For a monatomic solid, Y

is (Anderson,

1995)

¼ 251:2



1=3

k (Eq. 11)

where r is density (in g cm

3

), m is the atomic mass number (55.85 for

iron), and v

is the mean sound velocity (in km s

1

), given in terms of

the longitudinal and shear velocities as

2 þ



(Eq. 12)

The numerical factor in Eq. (11) is composed of the atomic constants

h, k, and N.

Body-centered cubic (bcc) iron is the phase of iron that exists at

ambient conditions. There is much data on this well-known phase.

We use the properties of bcc iron to explain principles such as the

evaluation of Eq. (11), but our chief interest lies in hexagonal close-

packed (hcp) iron, which is the most likely pure iron phase at core con-

ditions. In the evaluation of Eq. (11), properties of ambient bcc iron

are r,7:87 g cm

3

; v

,5:9kms

1

; v

,3:25 km s

1

; v

,3:62 km s

1

(note that v

is only slightly larger than v

). This gives

ðT ¼ 300Þ¼415 K at ambient conditions. Thus, above 415 K,

bcc iron is a classical solid, and below, it is a quantum solid. Since

the core is in the 5000–6000 K temperature range, its properties are

in the high T regime. Since the value of Y

=T at core temperatures

is of the order of 0.1, the exponential term in Eq. (8) is of the order

of 10

5

, insignificant compared to unity.

To find the lattice dynamical equation for g, divide Eq. (5) into two

factors as follows:

g ¼

ðaK

(Eq. 13)

GRU

NEISEN’S PARAMETER FOR IRON AND EARTH’S CORE 367

and evaluate each of the two parts separately from Eq. (8). From

calculus, aK

¼ð]P=]TÞ

. C

¼ð]U=]TÞ

, where U is the internal

energy. Using Eq. (9),



h

ðe

 1Þ

()

(Eq. 14)

where y

¼ hn

=kT.

Since U¼Fð]F=]TÞ

, then

U¼E

þ kT

j¼1

ðe

 1Þ

(Eq. 15)

and

¼ k

j¼1

ðe

 1Þ

j¼1

(Eq. 16)

Following Eq. (13), there are major cancellations, leaving

g ¼

(Eq. 17)

where the

g means that this Grüneisen parameter may be affected by

the approximation of the quasiharmonic assumption. Note that all fac-

tors containing y ¼ hn

=kT have cancelled out, leaving the temperature

dependence alone in C

, but since there is input of C

in both the

numerator and the denominator, there is very little temperature depen-

dence in either the low- or high-temperature regimes. In the very high-

temperature regime (such as found in the core), all C

are equal to k,

so the denominator in Eq. (17) is equal to 3Nk, while the numerator

is equal to k

. Thus, the high-temperature limit of the lattice

dynamical Grüneisen parameter is the arithmetic average of all mode

gammas (Barron, 1957).

g ¼

(Eq. 18)

Simplifications made by assuming a Debye solid

Evaluation of Eq. (18) is complicated by the fact that N (Avogadro’s

number) is quite large. We wish to reduce the summation in this equa-

tion from a limit of 3N to a lower value. We accomplish this by invok-

ing the assumptions of a Debye solid (Debye, 1912), which are: the

solid is monatomic and isotropic; its frequency spectrum (modal fre-

quency versus wave number k) is quadratic with a sharp cutoff at the

maximum frequency called the Debye frequency, v

; the slope of the

longitudinal and shear n

versus k curves is constant; and there are

no optic modes. Barron (1957) showed that invoking the properties

of a Debye solid reduces the sum over 3N modes in Eq. (18) to a

sum of 3 modes.

ðg

þ 2g

Þ (Eq. 19)

where g

is related to the longitudinal sound velocity and g

to the

shear sound velocity. In Eq. (19), g

has replaced g from Eq. (18)

because acoustic information is the sole input to gamma.

The mode gammas can be expressed in terms of velocity derivatives

(Anderson, 1995),





(Eq. 20)





(Eq. 21)

Sumino and Anderson (1984) evaluated g for bcc iron using Eq. (5)

and experimental values of a, K

, and C

. They found that g ¼ 1:81.

They also evaluated g, using the acoustic approximation to g

(Eq. (19)) and the measured elastic constant data under pressure and

found g ¼ 1:81. Since the derivation of Eq. (19) starts with Eq. (5),

it is concluded that the quasiharmonic assumption and the assumptions

of the Debye solid do not modify the value of g for bcc iron. This is a

way of demonstrating that bcc iron is a Debye solid. Debye’s theory of

a solid assumes that the whole vibrational spectrum can be represented

by the long wave limit where frequency is proportional to the wave

number ðn ¼ vkÞ. All modes are acoustic, each with the same average

velocity. Equation (19) can also be written in terms of the derivatives

of the bulk modulus and the shear modulus, G

ð]K

=]PÞ

þð4=3Þð]G=]PÞ

þð4=3ÞG

ð]G=]PÞ



(Eq. 22)

(Stacey and Davis, 2004).

Stacey and Davis (2004) stated, “The acoustic formula (for g) with-

stands critical scrutiny well. For application to the lower mantle it has

no serious rival.”

Thus, for the Debye solid, the 3N modal frequencies are replaced by

one frequency, n

, and one gamma,

¼

] ln n

] ln V



(Eq. 23)

Since hn

¼ kY

, the above can be replaced by

¼

] ln Y

] ln V



(Eq. 24)

A variant of Eq. (24) is



(Eq. 25)

which is true only for a Debye solid.

Equation (24) is used as follows. Measure Y

as a function of V,

and thus determine g as a function of V. Equation (25) is used to find

a shift in Y

corresponding to a shift in density.

A stringent test of the applicability of the theory of Debye solid to

properties of bcc iron is that the frequency spectra of the real solid

(called the phonon density of states, PDOS) has a sharp cutoff at a fre-

quency corresponding to the Debye temperature.

Proving epsilon (hcp) iron is a Debye solid

In the last section, bcc iron was proven to be a Debye solid. That is

only one of many proofs that have been made for this solid. Early in

the 20th century, a popular proof was to measure the entropy versus

T data for temperatures below the Debye temperature and show that

there was good agreement with the entropy calculated from the Debye

theory. Unquestionably, bcc iron is taken as a Debye solid. It is not

evident however, that hcp iron should be a Debye solid because this

phase of iron has hexagonal symmetry, which requires two atoms in

the lattice dynamic cell. Consequently, there are vibrational modes in

which both atoms move in the cell, but the center of mass remains

fixed. Such a vibration is an optical mode, and thus hcp iron has an

optical branch in its frequency spectrum, which usually implies that

there are modes with frequencies much higher than n

368 GRU

NEISEN’S PARAMETER FOR IRON AND EARTH’S CORE

For hcp iron, however, the two masses in the cell have equal values,

and lattice dynamic theory shows that in this case the frequencies

found in the optic branch are contained within a narrow band anchored

close to the maximum acoustic frequency. This means that within

the frequency spectrum f ðnÞ, called the phonon density of states

(PDOS), there is a clustering of modes near the maximum acoustic

value of f ðnÞ.

A criterion for the validity of the Debye solid is that the high-fre-

quency edge of the PDOS is the same (or nearly the same) as v

which is determined by Y

. Debye (1965) said, “it is not too important

to know the details of the frequency spectrum because at high tem-

perature one only has to know the number of degrees of freedom

[see Eq. (18)] and at low temperature the high frequency modes carry

less and less energy.” It is the maximum frequency of the PDOS that is

significant. The crucial test for hcp iron is to show that the PDOS has a

high-frequency, sharp cutoff close in value to v

A recent paper by Giefers et al. (2002) reported the measured PDOS

of hcp and bcc iron by nuclear inelastic scattering. Since hcp iron is a

high-pressure phase and does not exist at room pressure, the experi-

ment was done at P ¼ 28 GPa. An experiment was also done for bcc

iron at P ¼ 0 GPa (resulting data for both shown in Figure G56). Their

plots of the density of states, G(E), are reported in units of energy

(meV) instead of the usual units of frequency, but they report the cut-

off in terms of temperature, so the comparison with the Debye tem-

perature is eased. Note that for both phases of iron there is a sharp

cutoff of the spectrum with only a very small percentage of modes

seen above the cutoff. This is proof that both phases are Debye solids.

Further proofs come from the value of Y

The authors report that the value of the temperature corresponding

to the cutoff is 511 K for hcp iron (at 29 GPa) and 417 K for bcc iron

(at P ¼ 0). The value for hcp iron is to be compared with the measure-

ment of Y

reported by Anderson et al. (2001), 521 K at 29 GPa and

discussed in the next section. These values are sufficiently close to

conclude that hcp iron is a Debye solid. The value of Y

¼ 417 K

for bcc iron reported by Giefers et al. (2002) is to be compared with

¼ 415 K found from Eq. (11).

Anderson et al. (2001) also report that for hcp iron, the value of Y

at P ¼ 0 is 446 K. This value can also be used to predict the cutoff of

bcc iron by the bcc-hcp phase change using Eq. (25), and the ratio of

the uncompressed density of bcc iron to hcp iron is (7.87/8.28) with

g ¼ 1:7. The predicted Y

is 410 K, to be compared with 417 K from

the cutoff of the PDOS for bcc iron.

Experimental determination of lattice g(V) for iron

from Eq. (24)

The state of the art in diamond anvil pressure cells at high pressure has

improved so that by using a controlled intense x-ray beam from a syn-

chrotron radiation facility, determination of high quality powder x-ray

diffraction data is possible. (The intensity of the diffracted x-ray beam

is a measurable function of pressure.) For a Debye solid, the intensity

of the beam is given by the mean-square amplitude of atomic displace-

ments < u

>. Classical x-ray theory relates < u

> to the Debye

temperature, which Gilvarry (1956) gives as

< u

> ¼

ch

mkY

(Eq. 26)

where c is a numerical constant, and m is the atomic mass. Equation

(26) with c ¼ 3 is found in Willis and Pryor (1975). Using this equa-

tion and the measured values of < u

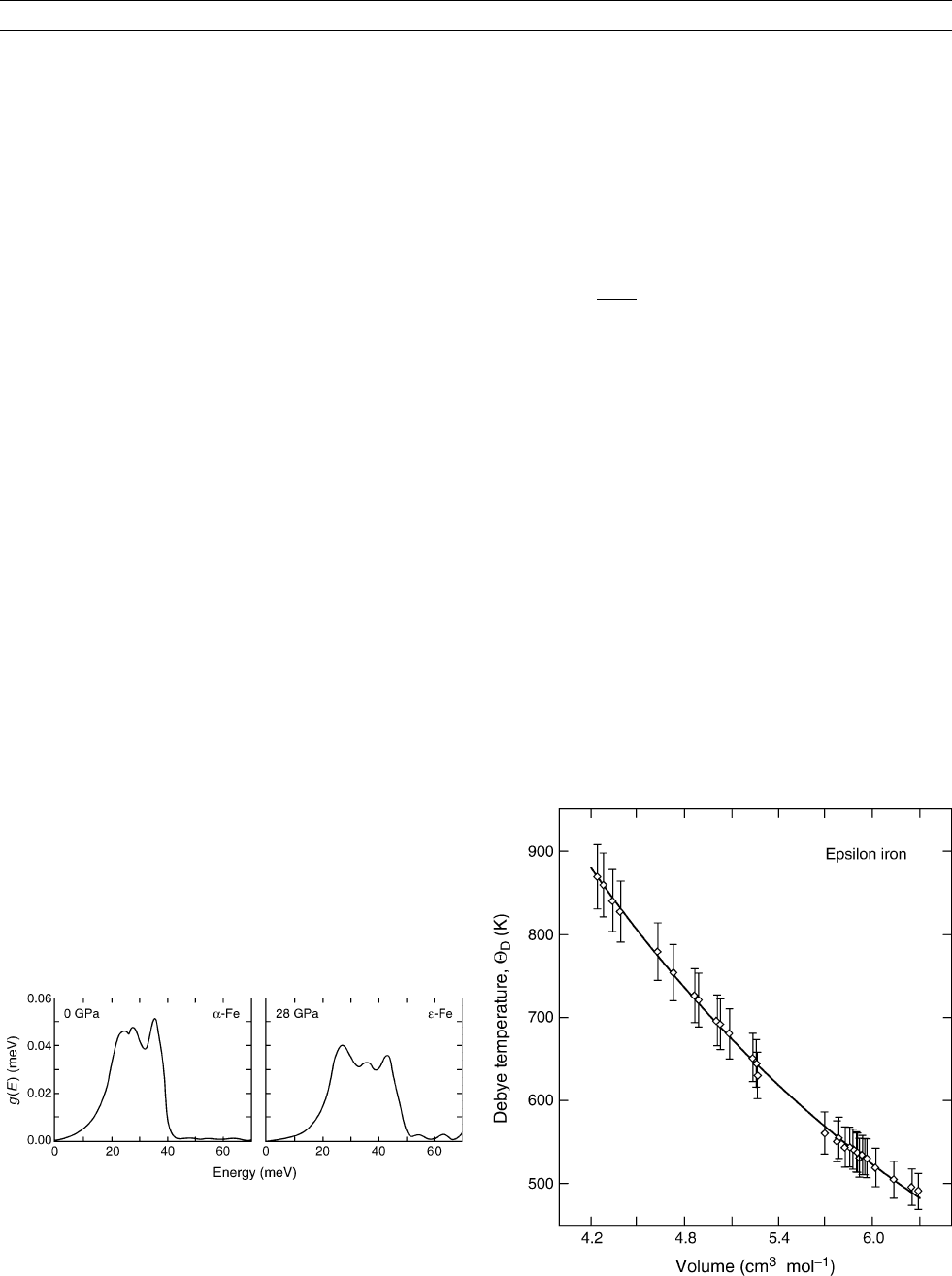
> versus V, Anderson et al.

(2001) measured the experimental values of Y versus V for hcp iron

from ambient pressure to P ¼ 300 GPa; these values are plotted in

Figure G57.

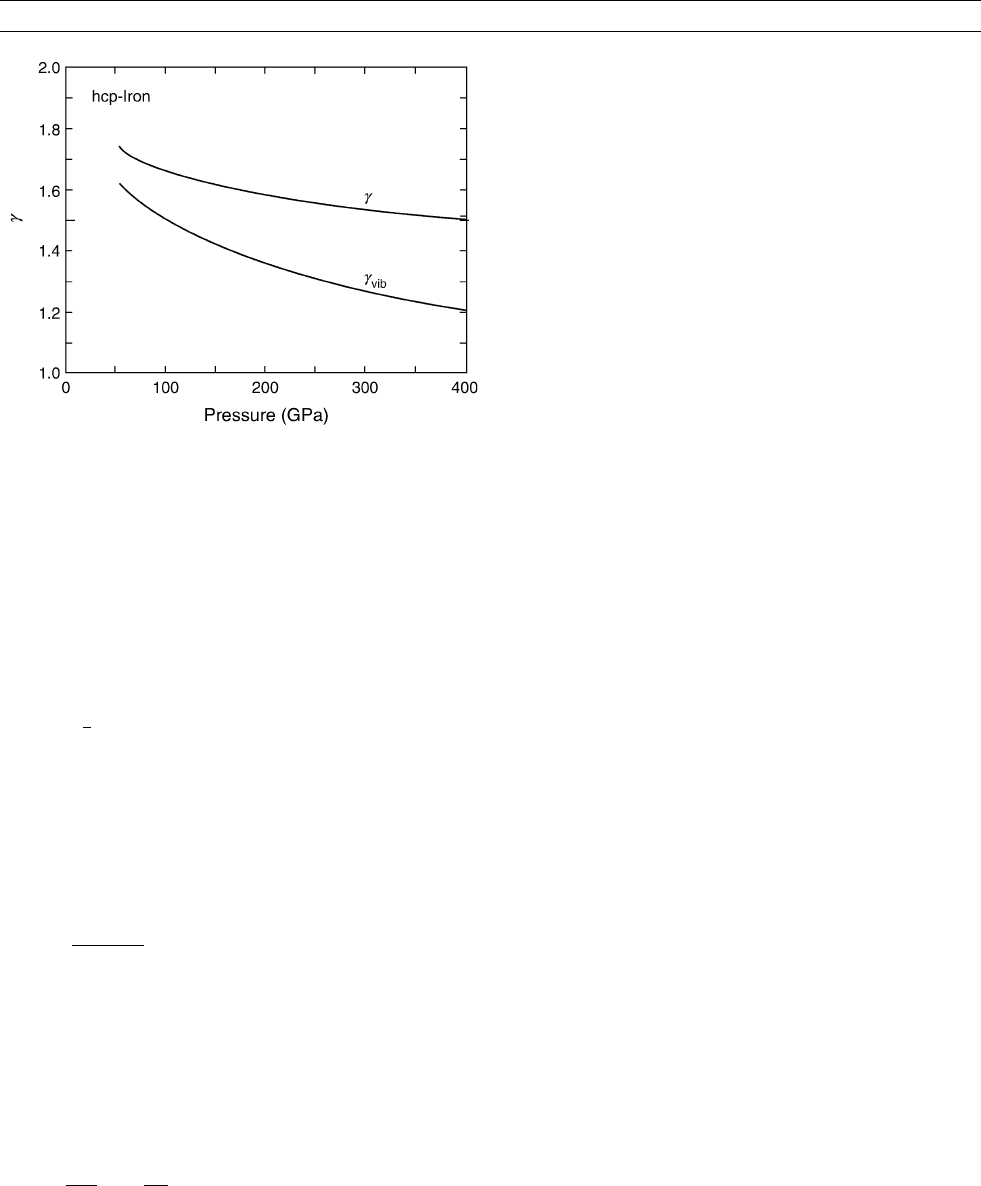
The value of g versus V was then found from Eq. (24). The data

are plotted in g  P space as the lower curve in Figure G58.Itis

seen that at 330 GPa, g

vib

decreases with pressure from the zero

pressure value of 1.7 to 1.2, the normal trend for nonmetallic solids.

But metals have an additional contribution to gamma not found in

nonmetallic solids arising from conduction electrons (often called

free electrons). This contribution to g is especially important at high

temperature. Since this electron contribution adds to the Helmholtz

energy, g as defined by Eq. (1) will be sensitive to the electronic

contribution. This means that for metals, the gamma found in this

section is only a part of that defined by Eq. (1) at core temperatures.

We therefore give the gamma shown in the lower curve of Figure

G58 a special name, g

vib

, indicating vibrational energy, or that arising

from the PDOS.

Figure G56 Experimental phonon density of states g(E ) of bcc iron

and hcp iron by Giefers et al. (2002). For hcp iron, the pressure is

28 GPa. The cutoff of bcc iron at P ¼ 0 is 40 meV (with a

corresponding temperature of 417 K). For hcp iron, the cutoff is

45 meV (with a corresponding temperature of 511 K). The Debye

temperature of bcc iron is 415 K, according to Eq. (11) , and the

Debye temperature of hcp iron is 520 K according to Anderson

et al. (2001) and as seen in Figure G57.

Figure G57 The experimental variation of Debye temperature Y

for hcp iron (Anderson et al., 2001). For P ¼ 28 GPa,

V ¼ 5:95 cm

mol

1

with a corresponding Y

¼ 519 K.

GRU

NEISEN’S PARAMETER FOR IRON AND EARTH’S CORE 369

Accounting for the electronic contribution to gamma

for iron

The electronic contribution to the specific heat in a metal has a domi-

nant effect at low T and sometimes at high T. The electronic contribu-

tion to specific heat, for example, is given by Kittel (1956) as

Dðe

Þk

T (Eq. 27)

where Dðe

Þ is the electronic density of states at the Fermi energy

level.

The important point is that C

increases steadily with T at high

T, whereas the lattice specific heat levels out for T > Y

and remains

independent of T (neglecting anharmonic terms). At 6000 K, the

specific heat of iron is 37% greater than the classical value of 3k per

atom, due to Eq. (27). From Eq. (27), the electronic Grüneisen

parameter is

] ln Dðe

] ln r

(Eq. 28)

Numerical evaluation of Eq. (28) (Bukowinski, 1977) gives g

¼ 1:5.

Thus, for iron the thermodynamic gamma of Sections and consists of

vib

, suitably modified by g

. The formalism for finding g for metals

is found in Bukowinski (1977); it requires the electronic specific heat

found from the electronic density of states (EDOS). Anderson (2002a)

found g

and g from g

vib

by using the PDOS and C

, as presented by

Stixrude et al. (1997). The theory of Bukowinski (1977) results in the

useful equation,

g ¼

vib

(Eq. 29)

where

¼ C

vib

þ C

(Eq. 30)

Some of the detailed calculations for hcp iron are given in Table G9.

Values in Table G9 were found for T increasing with P along the

solidus of hcp iron, as calculated by Anderson et al. (2003). The

value of g descends from 1.62 at P ¼ 135 GPa to 1.53 at 330 GPa, a

gradual decrease. The values of g in Table G9 are for the solid state

edge of melting, called the solidus. It is seen that g for the ICB

pressure (330 GPa) is 1.53, and for the CMB (135 GPa) it is 1.62.

Figure G58 shows g (the top curve), as well as g

vib

, versus P.

First princi ples calculations of gamma for liquid iron

The value of g is likely to be different for the liquid state than for the

solid state. Verhoogen (1980) first emphasized that the liquid state g

should be used for calculations of properties of Earth ’s core. The dif-

ference between the values of the liquid gamma (g

) and the solid

gamma ðg

Þ for iron is quite large at low pressure but small at high

pressure. The value of g

is 2.44 at P ¼ 0 (Stevenson, 1981), but that

of g

is 1.66 at P ¼ 0 (Boehler and Ramakrishnan, 1980) for bcc iron.

The value of g

decreases with pressure, becoming 1.63 at 30 GPa

(Chen and Ahrens, 1997), and then changes much more slowly with

further pressure, as we shall see. Measurements and/or calculations

of g

at core pressures have long been needed. Important progress

has been made in the theory of thermodynamic properties of con-

densed matter by calculations of parameter-free ab initio techniques

using quantum mechanics. The use of ab initio techniques for several

decades by many physicists has resulted in considerable advances in

understanding of solid state properties. Recently, ab initio methods

have advanced to the point that successful calculations of properties

of the liquid state at high pressure and high temperature have been

made.

Using ab initio methods, Alfè et al. (2002a) calculated 1.51 for g

P ¼ 330 GPa for iron along with the liquidus, giving T

¼ 6350 K.

This is quite close to the value of g

(1.53) at P ¼ 330 GPa for hcp

iron reported by Anderson et al. (2003), who found T

¼ 6050 K

for the solidus (see Table G9). Thus, Dg at the ICB pressure is small,

substantially smaller than at the CMB pressure, where g

¼ 1:52 (Alfè

et al., 2002a), while g

¼ 1:62 (Anderson et al., 2003).

For the solid state, Stixrude et al. (1997) reported g

¼ 1:5 for hcp

iron at ICB pressure from their ab initio calculations. Alfè et al.

(2001) reported g

¼ 1:52 for hcp iron at P ¼ 330 GPa, where the

solidus is found to be 6250 K, as compared to 1.53, as obtained by

Anderson et al. (2003). Thus, three laboratories have found very close

values of g

at 330 GPa, 1:5 < g

< 1:53.

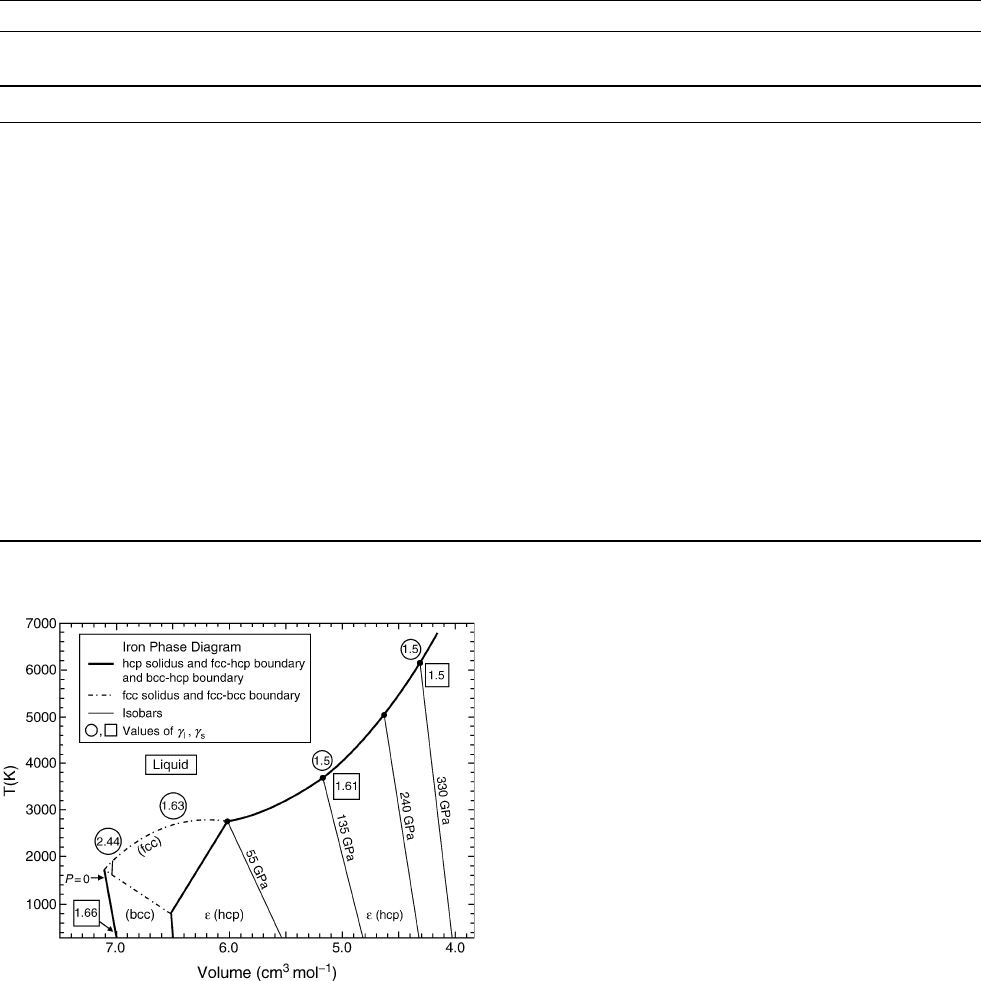
The various values for gamma are plotted on the phase diagram of

iron in Figure G59 (in the diagram, T is versus V with isobars as solid

lines).

We see that as the pressure increases, at core conditions, the differ-

ence between liquidus and solidus temperature values decreases and

Dg decreases, as well. This is interpreted to mean that as pressure

increases, the volume of crystallization diminishes. Indeed, Vocadlo

et al. (2003) report DV

¼ 0:77 cm mol

1

at 330 GPa, while

Anderson (2002b) report DV

¼ 0:55 also at 330 GPa from an analy-

sis of shock wave data. The values of g

and g

approach each other at

deep core pressures.

Core’s gamma: Consideration of impurities in iron

Structural changes

One approach for finding the properties of the core is to learn all that is

possible of pure iron at core pressure and then insert a certain quantity

of light elements into the iron structure and determine the resulting

changes. A number of problems arise, one of which is that the crystal-

lographic structure is reported to change from hcp when impurities are

added. The consensus is that hcp is the stable phase of pure iron, but

there is strong evidence that for the light impurities in iron, light sili-

con, sulfur, and oxygen, the high-pressure stable structure is bcc.

Figure G58 Variation of g

vib

and g for pure hcp iron with pressure

(Anderson et al., 2003). For the core range of pressure, g varies

between 1.62 at 135 GPa and 1.51 at 330 GPa. The calculations

were made with temperatures from the hcp solidus, so the values

of g represent the solid state edge of melting.

For further information on the Fermi energy level for metals, see

Kittel, Introduction to Solid State Physics, 2nd edn. New York: John

Wiley & Sons, 1956.

370 GRU

NEISEN’S PARAMETER FOR IRON AND EARTH’S CORE

Vocadlo et al. (2003) suggest that a mole of 4% silicon or sulfur,

either in combination or separately, may change the structure of hcp

iron to the bcc phase above 3000 K at high pressure.

When light impurities are placed in iron, its density decreases. The

percentage change in density, called the “core density deficit” (cdd), is

reported to be 4% to 7% for the outer core. The cdd is used to find the

DT drop at the ICB, giving the value of the liquidus temperature at

P ¼ 330 GPa for the core. This DT is called the “freezing point

depression.”

The effects of Si, S, and O impurities on the value of g

Alfè et al. (2002a) found from ab initio calcula tions that the core den-

sity deficit due to O, Si, and S, is 6.6%. The concentrations of these

light elements were found in a series of papers in which chemical equi-

librium between coexisting solid and liquid was treated. Ab initio

calculations by Alfè et al. (2002b) incorporating as a boundary condi-

tion the seismically determined density jump at the inner core-outer

core boundary found that substantial oxygen was required in the outer

core because silicon and sulfur could not account for the size of the

jump. From their conclusions of the amount and type of impurities

in the core, Alfè et al. (2002c) found the freezing point depression at

DT ¼700 K  100 K. In a subsequent paper, Alfè et al. (2002d)

reported the freezing point depression to be DT ¼800 K, a value

they have used in subsequent work. They estimated the core density

deficit, the isobaric density of pure hcp iron, less the corresponding

density of the core, to be 6.6% (Alfè et al., 2002c). The core

temperature at the ICB was found by subtracting 800 K from the

value 6350 K (the ab initio calculation of T

ð330 GPaÞ for hcp iron),

giving 5550 K.

As seen in the previous paragraph, it is concluded from ab initio

studies that

1. The difference between g

for pure iron and g

for the core at the

ICB is only 0:02 despite the addition of 9% oxygen and 9%

Si/Si to the hcp structure. This difference is trivial.

2. The difference between g

and g

at the ICB for both the core and

hcp iron is 0:01; again, it is trivial.

3. The value of g

at the ICB of the core found by Alfè et al. (2002b) is so

close to 1.5 that it has been taken to be 1.5 in the paper by Gubbins

et al. (2003) in which D. Alfè and G.D. Price were coauthors.

4. The value of g

¼ 1:5 at the ICB is associated with a cdd of 6.6%

and a freezing point depression of 800 K.

5. The value of g

is virtually unchanged from the CMB pressure to

the ICB pressure.

The effect of Ni in the core on the value of g

The relative abundances of Fe and Ni in the core are probably about

1

(McDonough and Sun, 1995). Thus, we consider the effect of

0.90

-Ni

0.10

in place of Fe. Mao et al. (1990) found that r for

0.80

-Ni

0.20

at 330 GPa and 300 K is about 2% higher than for pure

Fe. Therefore, the alloy Fe

0.90

-Ni

0.10

at the ICB is 1% denser than

hcp iron.

Figure G59 Values of g

(solid state) and g

‘

(liquid state) plotted

on the phase diagram of iron (T versus V with isobars as shown).

Table G9 Heat capacity, g

vib

and g along the calculated solidus of hcp iron

V (cm

mol

1

) T

(K)

P (GPa) C

vib

6.060 2790 55.0 1.331 1.62 1.74

6.000 2840 58.1 1.336 1.61 1.73

5.800 3040 71.6 1.360 1.57 1.70

5.600 3270 88.0 1.390 1.53 1.68

5.500 3400 97.5 1.407 1.51 1.67

5.300 3690 119.5 1.445 1.47 1.64

5.181 3880 135.0 1.472 1.44 1.62

5.100 4030 146.5 1.491 1.43 1.62

5.000 4230 162.2 1.517 1.41 1.61

4.900 4440 179.7 1.545 1.35 1.60

4.800 4660 199.2 1.575 1.37 1.59

4.700 4910 220.8 1.607 1.35 1.58

4.620 5120 240.0 1.633 1.32 1.56

4.600 4170 244.9 1.640 1.32 1.56

4.500 5460 271.7 1.675 1.30 1.55

4.400 5770 301.7 1.712 1.28 1.54

4.316 6050 330.0 1.743 1.25 1.53

4.300 6100 335.3 1.749 1.25 1.53

4.200 6450 372.8 1.788 1.23 1.52

4.100 6830 414.9 1.827 1.20 1.50

Anderson et al. (2003).

GRU

NEISEN’S PARAMETER FOR IRON AND EARTH’S CORE 371

A 1% increase in density would have virtually no effect on g

or g

because g is nearly constant with pressure in the vicinity of the ICB

(Figures G58 and G59). From the data plotted in both figures, a 1%

change in density changes g only slightly in the third significant figure.

Thus, the value of g

is insensitive to the addition of nickel to iron.

In the ab initio approach, all physical properties are found from

derivatives of the Helmholtz free energy, F, which is made to account

for all atoms (Fe and impurities, if any) in their respective lattice sites.

The physical properties of the core are found from the core’s

free energy. These properties are different from those found from

the free energy of pure iron, except for the value of g

, which is vir-

tually the same for both cases. How can this be explained? The value

of g

changes with volume, but in the case of iron, the value of

gamma changes very slowly with volume at core pressures, as shown

in Figure G58. Consider the drop in temperature called the freezing

point depression, DT

¼800 K. The relative change in volume

due to freezing point depression is DV=V ¼Dr=r ¼ aDT at the

ICB. The value of a varies from 1:07  10

5

at 6350 K and 330

GPa (for pure iron) to 0:99  10

5

and 330 GPa for the core (D. Alfè,

personal communication). If we know a and DT, then we can calculate

Dr=r, the percent density change. The average a  DT gives

Dr=r ¼0:85%, less than but opposite to the 1% increase arising

from placing 10% Ni in the Fe-Ni alloy.

Finding core properties independent of pure

iron properties

Stacey (2000) introduced a new equation of state called the K-primed

approach because he found all EoSs used in geophysical treatment

of Earth’s mantle to be in error with regard to the higher derivatives,

especially the derivative of K

with respect to V. Stacey successfully

applied his K-primed equation of state to the Earth’s mantle and core.

In Stacey and Davis (2004), thermal core properties were extracted

directly from seismic data of Earth without the intermediate step of

using properties of pure iron. The values of gamma for the core they

report, to three significant figures, are 1.39 at the CMB pressure

and 1.44 at the ICB pressure. They also report that the values of T

for the liquidus are 5000 K and 3739 K, for the ICB and CMB,

respectively.

Summary and conclusions

Our prime focus is on the value of g at pressures of 135 GPa (CMB)

and 330 GPa (ICB) for the liquidus and the solidus of hcp iron and

for the liquidus of the outer core and the solidus of the inner core.

The values of g and associated properties of thermal expansivity a

and melting temperature T

described in the previous sections are

summarized in Table G10.

It is noted that the values of g

at the ICB from the two approaches

(ab initio and thermal physics) agree quite well. There is good agree-

ment on the value of g

, but the value reported from the K-primed EoS

approach is about 0.1 less than that reported from the ab initio

approach.

The ab initio approach yields the largest range of results, giving

values for both g

and g

and for both hcp iron and the core, whereas

the thermal physics approach is limited to g

for hcp iron and the inner

core. The K-primed EoS approach is limited to g

for the outer core

and g

for the inner core. An advantage of the K-primed EoS approach

is that information about the chemistry—in particular, the concentra-

tions of the various impurity elements—is not required to obtain g

of the core. However, this is also a disadvantage because no informa-

tion can be given to geochemists about impurities. In contrast, the

Table G10 Values of g, T

, and a for pure hcp iron and Earth’s core

Parameters Ab initio calculations

Thermal physics

measurements and theory

K-primed EoS

and seismic data

Pure hcp iron, solidus, 330 GPa

1.50 1.53

(K) 6250 6050

að10

5

1

Þ 1.07 0.7

Pure hcp iron, solidus 135 GPa

1.519 1.62

(K) 4734 4062

að10

5

1

Þ 1.78 2.5

Pure hcp iron, liquidus 330 GPa

1.518

(K) 6350

að10

5

1

Þ 1.072

Pure hcp iron, liquidus 135 GPa

‘

1.520

(K) 4734

að10

5

1

Þ 1.78

Core, liquidus, 330 GPa

1.50 1.391

(K) 5550 5100 5001

að10

5

1

Þ 0.99 0.971

Core, liquidus, 135 GPa

1.53 1.443

(K) 4111 4100 3739

að10

5

1

Þ 1.70 1.804

Alfè et al. (2001, 2002a-d), Vocadlo et al. (2003).

Anderson (2002b); Anderson et al. (2003), Isaak and Anderson (2003).

Stacey and Davis (2004).

372 GRU

NEISEN’S PARAMETER FOR IRON AND EARTH’S CORE

ab initio approach can give valuable results about core impurities: it

was shown that sulfur and silicon as impurities in iron cannot account

for the seismic density jump at the ICB, but about 8 mol% oxygen in

the outer core is consistent with the seismic jump.

From the results of the ab initio calculations, the value of g

is vir-

tually constant from the ICB pressure to the CMB pressure, varying

by 1.3%. The variation using the K-primed EoS approach is somewhat

larger, 5.7%. If g

is assumed to be constant over this range, the rela-

tionship between T

and density r given by Eq. (7) is simplified,



(Eq. 31)

Using the ratio of the seismic density of the core at the CMB to that at

the ICB (12166.34/9903.49), Eq. (31) becomes



¼ 0:7344 for g

¼ 1:5

¼ 0:7466 for g

¼ 1:42

Thus, if Eq. (31) is used to find T

(CMB) from T

(ICB), the

answer will differ by only 1.2% if one uses the ab initio gamma in

comparison with the K-primed EoS gamma (starting out with the same

value of T

). If one uses the ab initio data or the thermal physics data

and is satisfied that the value of T

(P) is rounded to three significant

figures, then the value of g

can be rounded to three significant figures

for the entire outer core region. The value of g

¼ 1:5 was used by

Gubbins et al. (2003) throughout the core in their analysis of the geo-

dynamo. The value of g

for the inner core decreases very slowly with

the depth from its value at the ICB pressure. Table G9 shows that g

(listed in the table as gamma) drops from 1.53 at the ICB (330 GPa)

to 1.52 at a pressure of 372.8 GPa; by interpolation gamma is 1.525

at the Earth’s center, which has a pressure of 363.9 GPa. One may

as well use g

¼ 1:53 for calculation of T

at the Earth’s center. We

need to know the temperature of the core; this requires DT

, the freez-

ing point depression from pure iron. Alfè et al. (2002c) report

¼800 K. Thus, for the temperature at the ICB pressure, one

finds T

ðcoreÞ¼5 550 K from the solidus at ICB (6250 K) for

the ab initio approach, and T

ðcoreÞ¼5 250 K from the thermal

properties approach. The K-primed EoS approach leads to

ðcoreÞ¼5000 K. This calculation using Eq. (31) is T

ðE centerÞ=

ðICBÞ¼1:1213, giving, for Earth’s center, 6111 K for the ab initio

ICB value (5450 K) and 5456 K for the thermal physics ICB value

(5250 K). The K-primed EoS approach gives 5030 K for Earth’s

center.

Acknowledgments

The author gratefully acknowledges the data on g, T

ðKÞ, and a (listed

in Table G10), from Dario Alfè’s work (some unpublished), which

were sent to him on request.

Orson L. Anderson

Bibliography

Alfè, D., Price, G.D., and Gillan, M.J., 2001. Thermodynamics of hex-

agonal close packed iron under Earth ’s core conditions. Physical

Review B, 64:1–16.04123,

Alfè, D., Price, G.D., and Gillan, M.J., 2002a. Iron under Earth’s core

conditions: thermodynamics and high pressure melting from ab-

initio calculations. Physical Review B, 65(118): 1–11.

Alfè, D., Gillan, M.J., and Price, G.D., 2002b. Composition and

Earth’s core constrained by combining ab initio calculations and

seismic data. Earth and Planetary Science Letters, 195 :91–98.

Alfè, D., Gillan, M.J., and Price, G.D., 2002c. Ab-initio chemical

potentials of solid and liquid solutions and the chemistry of the

Earth’s core. Journal of Chemical Physics, 116: 7127–7136.

Alfè, D., Gillan, M.J., and Price, G.D., 2002d. Complementary

approach to ab-initio calculations of melting properties. Journal

of Chemical Physics, 116: 6170–6177.

Anderson, O.L., 1995. Equations of State for Geophysics and Ceramic

Science. New York: Oxford University Press, 405 pp.

Anderson, O.L., 2002a. The power balance at the core-mantle bound-

ary. Physics of the Earth and Planetary Interiors, 131:1–17.

Anderson, O.L., 2002b. The three dimensional phase diagram of iron.

In Karato, S., Dehant, V., and Zatman, S. (eds.), Core Structure

and Rotation. Washington, DC: American Geophysical Union.

Anderson, O.L., Dubrovinsky, L., Saxena, S.K., and Le Bihan, T.,

2001. Experimental vibrational Grüneisen ratio value for e-iron up

to 330 GPa at 3000 K. Geophysical Research Letters, 28: 399–402.

Anderson, O.L., Isaak, D.G., and Nelson, V.E., 2003. The high-pres-

sure melting temperature of hexagonal close-packed iron deter-

mined from thermal physics. Journal of Physics and Chemistry

of Solids, 64: 2125–2131.

Barron, T.H.K., 1957. Grüneisen parameters for the equation of state

of solids. Annals of Physics, 1:77–89.

Boehler, R., and Ramakrishnan, J., 1980. Experimental results on the

pressure dependence of the Grüneisen parameter. A review. Jour-

nal of Geophysical Research

, 85: 6996–7002.

Bukowinski, M.S.T., 1977. A theoretical equation of state for the inner

core. Physics of the Earth and Planetary Interiors, 14: 333–339.

Chen, G.Q., and Ahrens, T.J., 1977. Sound velocities of liquid g and

liquid iron under dynamic compression (abstract). EOS Transac-

tions of the American Geophysical Union, 78: P757.

Debye, P., 1912. Theorie der spezifischen wärmen. Annals of Physics

(Berlin), 39: 789–839.

Debye, P., 1965. The early days of lattice dynamics. In Wallis, R.I.

(ed.) Lattice Dynamics: Proceedings of an International Confer-

ence. Oxford, UK: Pergamon Press, pp. 9– 17.

Giefers, H., Lubbers, P., Rupprecht, K., Workman, G., Alfè, D., and

Chumakov, A.I., 2002. Phonon spectroscopy of oriented hcp iron.

High Pressure Research, 22: 501–506.

Gilvarry, J.J., 1956. The Lindemann and Grüneisen laws. Physical

Review, 102: 308–316.

Grüneisen, E., 1926. The state of a solid body. In Handbuch der

Physik, vol. 10, Berlin: Springer-Verlag, pp. 1–52, (English trans-

lation, NASA RE 2-18-59W, 1959).

Gubbins, D., Alfè, D., Masters, G., Price, G.D., and Gillan, M.J.,

2003. Can the Earth’s dynamo run on heat alone? Geophysical

Journal International, 155(2): 609–622, doi: 10.1046/j.1365-

246X.2003.02064.x.

Gubbins, D., Alfè, D., Masters, G., Price, G.D., and Gillan, M., 2004.

Gross thermodynamics of 2-component core convection. Geophy-

sical Journal International, 157: 1407– 1414.

Isaak, D.G., and Anderson, O.L., 2003. Thermal expansivity of hcp

iron at very high pressure and temperature. Physica B, 328: 345–354.

Kittel, C., 1956. Introduction to Solid State Physics, 2nd edn. New

York: Wiley, 617 pp.

Mao, H.K., Wu, Y., Chen, C.C., Shu, J.F., and Jephcoat, A.P., 1990.

Static compression of iron to 300 GPa and Fe

0.8

0.2

alloy to 200

GPa. Journal of Geophysical Research, 95: 21691–21693.

McDonough, W.F., and Sun, S., 1995. The composition of the Earth.

Chemical Geology, 120: 228–253.

Slater, J.C., 1939. Introduction to Chemical Physics, 1st edn. New

York: McGraw-Hill.

Stacey, F.D., 2000. The K-primed approach to high pressure equations

of state. Geophysical Journal International, 128: 179–193.

Stacey, F.D., and Davis, P.M., 2004. High pressure equations of state

with applications to the lower mantle and core. Physics of the

Earth and Planetary Interiors, 142: 137–184.

GRU

NEISEN’S PARAMETER FOR IRON AND EARTH’S CORE 373

Stevenson, D.J., 1981. Models of the Earth’s core. Science, 214:

611–619.

Stixrude, L., Wasserman, E., and Cohen, R.E., 1997. Composition and

temperature of the Earth’s inner core. Journal of Geophysical

Research, 102: 24729–24739.

Sumino, Y., and Anderson, O.L., 1984. Elastic constants of minerals.

In Carmichael, R.S. (ed.) CRC Handbook of Physical Properties

of Rocks. Boca Raton, FL: CRC Press, pp. 39–138.

Verhoogen, J., 1980. Energetics of the Earth. Washington, DC:

National Academy of Sciences, 139 pp.

Vocadlo, L., Alfè, D., Gillan, M.J., Wood, I.G., Brodholt, J.P., and

Price, G.D., 2003. Possible thermal and chemical stabilization of

body-centred-cubic iron in the Earth’s core. Nature, 424: 536–538.

Willis, B.T.M., and Pryor, A.W., 1975. Thermal Vibrations in Crystal-

lography, 1st edn. London, UK: Cambridge University Press.

Cross-references

Core Composition

Core Density

Core Properties, Theoretical Determination

Core, Adiabatic Gradient

Core-Mantle Boundary, Heat Flow Across

Higgins-Kennedy Paradox

Shock Wave Experiments

374 GRU

NEISEN’S PARAMETER FOR IRON AND EARTH’S CORE

HALLEY, EDMOND (1656–1742)

Edmond Halle y (Figure H1) was born in London in 1656 and educated

at St. Paul’s School in London and the Queen’s College, Oxford,

which he left in 1676 without a degree to catalog southern stars and

observe a transit of Mercury on the island of St. Helena. He also mea-

sured magnetic inclination on this voyage, in the Cape Verdes and on

St Helena. On his return the Royal Society elected him a fellow. He

visited Johannes Hevelius in Danzig and G.D. Cassini in Paris and

observed with them. He became clerk to the Royal Society in 1686. He

prompted Newton to write the Philosophiae Naturalis Principia Mathe-

matica and published it himself. He was often at sea, surveying and

diving for salvage until he was elected Savilian Professor of Geometry

in Oxford in 1704. He became the second Astronomer Royal in 1720.

The Westward Drift (q.v.)

In 1680, it was known that the major deviations of the Earth’s field from

that of a uniformly magnetized sphere appeared to move westward.

Halley selected representative observations of the variation (magnetic

declination) from 1587 to 1680, and from New Zealand (170



E) to

Baffin Bay (80



W). They came from mariners’ reports, and perhaps

from collections not to be found now. He found that the westward drift

was not the same everywhere (Halley, 1683). He argued that the exten-

sive anomalies had much deeper sources than iron near the surface that

Descartes (Descartes, 1644) and Gilbert (q.v.) proposed. He suggested

that the Earth had a shell with one pair of poles and a core with another

pair, the two in relative rotation (Halley, 1692). Would there be life in

the space between the core and the shell? Other worlds in other places

and at other times were then seriously contemplated.

The Atlantic cruises

In October 1698, Halley sailed as a captain in the Royal Navy in a ship

built for him by the government, to cruise around the Atlantic and

observe the magnetic variation for navigation, the first-ever scientific

naval surveys (Thrower, 1981). He measured the angle between

compass north and geographic north as established by the Sun’s posi-

tion at rise or set. He found his latitude from the elevation of the Sun at

noon. Longitude at sea was much more difficult, and sometimes had

gross errors. Halley had delays, bad weather, and difficult officers,

and was too late in the season to go into the South Atlantic. His second

cruise from September 1699 to September 1700 accomplished much

more, and he went further into the Antarctic ice than anyone before.

Halley’s chart of isogonic lines over the Atlantic hung in the Royal

Society building for many years but is now lost. Many printed copies

were published, the first isarhythmic chart of any variable to have been

published. There may already have been private manuscript charts and

Athanasius Kircher (q.v.) had written of one in his Magnes. (Kircher,

1643) Halley claimed, justly, that his chart was the first with isogonic

lines to have been printed and published: He was a founder of modern

cartography. His lines were known as Halleyan lines, and were soon

used for other data such as temperature and depth of water. About two

hundred years later Christopher Hansteen (q.v.)andW. van Bemmelen

(q.v.), having access to the logs of Dutch ships, compiled worldwide

isogonic charts at regular epochs. His chart for 1700 is generally close

to Halley’s where they overlap.

Figure H1 Edmond Halley.

Professor Sir Alan Cook died in August 2004 after completing this

article. Final minor changes were made by the editors, who take full

responsibility for any omissions or errors.