Gubbins D., Herrero-Bervera E. Encyclopedia of Geomagnetism and Paleomagnetism

Подождите немного. Документ загружается.

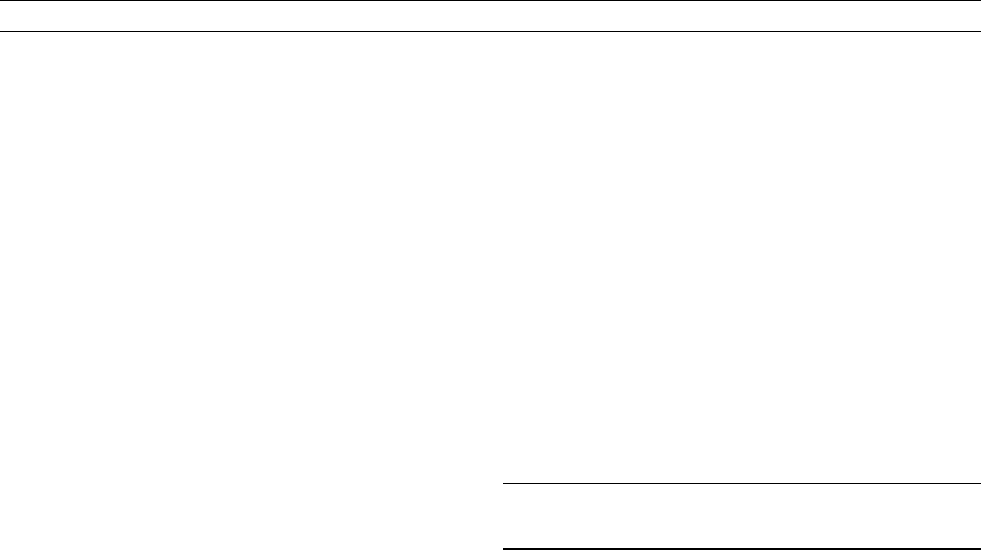
Fabian, K., 2000. Acquisition of thermoremanent magnetization in

weak magnetic fields. Geophysical Journal International, 142:

478–486.

Fox, J.M.W., and Aitken, M.J., 1980. Cooling-rate dependence of ther-

moremanent magnetisation. Nature, 283: 462–463.

Halgedahl, S.L., and Fuller, M., 1980. Magnetic domain observations

of nucleation processes in fine particles of intermediate titanomag-

netite. Nature, 288:70–72.

Halgedahl, S.L., and Fuller, M., 1983. The dependence of magnetic

domain structure upon magnetization state with emphasis on

nucleation as a mechanisms for pseudo-single-domain behaviour.

Journal of Geophysical Research, 88: 6506–6522.

Halgedahl, S.L., Day, R., and Fuller, M., 1980. The effect of cooling

rate on the intensity of weak-field TRM in single domain magne-

tite. Journal of Geophysical Research, 85: 3690–3698.

Heider, F., Halgedahl, S.L., and Dunlop, D.J., 1988. Temperature

dependence of magnetic domains in magnetite crystals. Geophysi-

cal Research Letters, 15: 499–502.

McClelland, E., and Sugiura, N., 1987. A kinematic model of TRM

acquisition in multidomain magnetite. Physics of the Earth and

Planetary Interiors, 46:9–23.

Menyeh, A., and O’Reilly, W., 1998. Thermoremanence in monoclinic

pyrrhotite particles containing few domains. Geophysical Research

Letters, 25(18): 3461–3464.

Metcalf, M., and Fuller, M., 1987. Domain observations of titanomag-

netites during hysteresis at elevated temperatures and thermal

cycling. Physics of the Earth and Planetary Interiors, 46:

120–126.

Néel, L., 1949. Théorie du traînage magnétique des ferromagnétiques

en grains fins avec applications aux terres cuites. Annales de Geo-

physique, 5:99–136.

Néel, L., 1955. Some theoretical aspects of rock magnetism. Advances

in Physics, 4: 191–243.

Özdemir, Ö., and Dunlop, D.J., 1997. Effect of crystal defects and

internal stress on the domain structure and magnetic properties of

magnetite. Journal of Geophysical Research, 102:20211–20224.

Özdemir, Ö., and Dunlop, D.J., 2002. Thermoremanence and stable

memory of single-domain hematite. Geophysical Research Letters,

29:doi:10.1029/2002GL015597.

Özdemir, Ö., and O’Reilly, W., 1982. An experimental study of ther-

moremanent magnetization acquired by synthetic monodomain

titanomaghemites. Journal of Geomagnetism and Geoelectricity,

34: 467–478.

Schmidt, V.A., 1973. A multidomain model of thermoremanence.

Earth and Planetary Science Letters, 20: 440–446.

Shcherbakov, V.P., McClelland, E., and Shcherbakova, V.V., 1993. A

model of multidomain thermoremanent magnetization incorporat-

ing temperature-variable domain structure. Journal of Geophysical

Research, 98: 6201–6216.

Stacey, F., 1958. Thermoremanent magnetization (TRM) of multi-

domain grains in igneous rocks. Philosophical Magazine, 3:

1391–1401.

Stacey, F., and Banerjee, S.K., 1974. The Physical Principles of Rock

Magnetism. Elsevier, Amsterdam.

Stoner, E.C., and Wohlfarth, E.P., 1948. A mechanism of magnetic

hysteresis in heterogeneous alloys. Philosophical Transactions of

the Royal Society of London, A240: 599– 642.

Sugiura, N., 1980. Field dependence of blocking temperature of

single-domain magnetite. Earth and Planetary Science Letters,

46: 438–442.

Thellier, E., 1938. Sur l’aimantation des terres cuites et ses applica-

tions géophysiques. Annales de. l’Institut de Physique du Globe,

Université de Paris, 16: 157–302.

Thellier, E., and Thellier, O., 1959. Sur l’ intensité du champ magné-

tique terrestre dans le passé historique et géologique. Annales de

Géophysique, 15: 285–376.

Tucker, P., and O’Reilly, W., 1980. The acquisition of thermoremanent

magnetization by multidomain single-crystal titanomagnetite. Geo-

physical Journal of the Royal Astronomical Society,

60:21–36.

Winklhofer, M., Fabian, K., and Heider, F., 1997. Magnetic blocking

temperatures of magnetite calculated with a three-dimensional

micromagnetic model. Journal of Geophysical Research, 102:

22695–22709.

Cross-references

Archeomagnetism

Magnetic Anisotropy, Sedimentary Rocks and Strain Alteration

Magnetic Domain

Magnetic Susceptibility

Magnetization, Chemical Remanent (CRM)

Magnetization, Isothermal Remanent (IRM)

Magnetization, Natural Remanent (NRM)

Magnetization, Viscous Remanent (VRM)

MAGNETIZATION, THERMOREMANENT, IN

MINERALS

Thermoremanent magnetization

Perhaps the best understood of the primary magnetizations, of natural

rocks and specimens, is thermal remanent magnetization (TRM). Most

of the natural rocks are magnetized primarily by the geomagnetic field

(30000 nT) and acquire natural remanent magnetization (NRM).

Magnetic minerals acquire TRM when they are contained within the

rock that is cooled in an external magnetic field from temperatures

above the minerals’ blocking temperatures. Blocking of remanent

magnetization at a specific temperature results in locking of a specific

direction and intensity of magnetization as it becomes stable on the

timescale of the TRM acquisition.

The generally recognized first-order theory of TRM can be applied

only to small uniformly magnetized grains (Néel, 1949) and it provides

a reasonable explanation for the intensity of TRM vs inducing field. The

theory explains the changes of stability of TRM with temperature and

with the inducing field, explaining how a rock can maintain a TRM

record for billions of years. This theory can also provide an explanation

on how the secondary component of magnetization of a rock can be

removed from the primary one.

However, besides being useful only for small single-domain (SD)

grains it is also less successful in explaining TRM acquisition for more

intense ambient fields (1 mT). According to Neel’s theory, the TRM

reaches saturation, in lower fields than actually measured on speci-

mens (10 mT). This effect was assigned to particle interaction and

long axis dispersions (Stacey and Banerjee, 1974).

In general, the TRM is not carried only by a small single-domain

(SD) fraction of magnetic mineral grains. When the volume of the

grain is larger (>0.5 m m for magnetite mineral) the demagnetizing

field (caused by magnetic sources distributed on the surface of the

grain) has a slightly different geometry than the pattern of the uniform

magnetization (Figure M135). This geometry causes inhomogeneity of

magnetization of the larger grains that is replaced by more energeti-

cally favorable state containing domain walls bounding volume with

reversed magnetic moments.

Neel first attempted to construct the theory for multidomain materi-

als (Néel, 1955). Stacey (1963) and Everitt (1962) applied a concept of

Barkhausen discontinuities, small jumps of the domain walls into the

new position, believed to be due to crystal imperfections. The resis-

tance of the domain wall motion was thought to be responsible for

remanent magnetism in MD grains. As the smaller MD grains were

616 MAGNETIZATION, THERMOREMANENT, IN MINERALS

more stable than larger MD grains, Stacey invented the term pseudo-

single-domain (PSD) grains for grains slightly larger than SD grains

(Stacey, 1963).

Because, in general, small grains of magnetite have 2–3 orders of

magnitude larger TRM intensity than larger MD grains. For some time

it was thought that the TRM of MD grains is negligible (Hargraves and

Young, 1969; Hoye and Evans, 1975). More small grains are present

in rocks than apparently visible, resulting from the formation of the

iron oxides through oxidation inside the silicates.

The intensity of the remanent magnetization acquired by rocks is

determined by an unknown strength of the ambient magnetic field,

an unknown magnetic mineral composition, and an unknown tempera-

ture history of the sample. Stacey pointed out in his theory of multido-

main TRM (Stacey, 1958) that because the demagnetizing energy falls

off more slowly with temperature than any other, the condition under

which TRM is first acquired is simply the minimization of the internal

field. This guarantees that at least at this temperature the TRM is

related only to the magnetostatic energy and the demagnetizing energy.

Néel’s theory of MD TRM is incomplete since it fails to describe many

aspects of pTRM (partial TRM) behavior (Néel, 1955; Shcherbakova

et al., 2000). There the blocking occurs at temperature T

when mag-

netic coercivity increases high enough to pin domain walls against the

demagnetizing field. For TRM of SD grains at room temperature,

), magnetic remanence was frozen in high temperature equili-

brium distribution achieved by thermally excited transitions among

the different magnetic states. Transitions cease below the T

, because

in the course of cooling, the energy barriers between different magne-

tization states grow larger than the available thermal energy. For both

SD and MD states the resulting magnetization, composed of many

magnetic moments, is in the direction of and for mineral specific field

range (Kletetschka et al., 2004) proportional to the applied magnetic

field B. Efficiency e(T

)ofM

) of SD grains of saturation rema-

nence J

), volume V, and saturation magnetization J

) is (Néel,

1949):

EðT

Þ¼

ðT

¼ tanh

mVJ

ðT

ÞB



; (Eq. 1)

with m

¼ 4p  10

–7

, and k ¼ 1.38  10

–23

–1

On the timescale 50–100 s:

ðT

ÞB

ðT



¼ 2lnðf

tÞ50;

where B

) is a critical field for moment rotations in the absence of

thermal energy (microcoercivity), and frequency of moment fluc-

tuation f

 10

1

. Therefore, from Eq. (1) one can derive for

small fields (E  1):

EðT

Þ¼

50B

ðT

(Eq. 2)

In most fine-grained magnetic material, a typical efficiency E(T

)ofther-

moremanent magnetization M

) acquired in the geomagnetic field is

about 1% (Wasilewski, 1977, 1981; Cisowski and Fuller, 1986;

Kletetschka et al., 2000a). This small efficiency is consistent with the

) acquisition curves for magnetite (Dunlop and Waddington, 1975;

Tucker and O’Reilly, 1980; Özdemir and O’Reilly, 1982) with grain sizes

covering the range from the single-domain (SD) to multidomain (MD)

magnetic states. However, M

) experiments with hematite (Kletetschka

et al., 2000b,c; Dunlop and Kletetschka, 2001; Kletetschka et al., 2002)

showed e >10%.

Experimental TRM constrains for theory

The following part is largely reiteration of the results from Kletetschka

et al. (2004). There in an attempt to reconcile the contrast between

TRM acquisition of hematite and magnetite series of magnetic M

Figure M135 Intensities of the ambient magnetic field B (tesla) against thermoremanent efficiencies e of hematite (Fe

), magnetite

(Fe

), iron-nickel alloy (FeNi) and iron (Fe). The pyrrhotite data (Fe

) are from Dekkers (1989). Straight lines are drawn

according to B ¼ aJe , where a is a dimensionless constant equal to 0.0046 (see Figure M137a) at 300 K, and J ¼ m

where

is permeability of vacuum and J

is saturation magnetization at 300 K. Magnetization efficiency e is defined as e ¼ M

, the

ratio of thermoremanence to saturation remanence. Single-domain (SD) and acicular (elongated crystal parallel to the applied field)

magnetite data are redrawn from Dunlop and Argyle (1997) and Dunlop and West (1969), respectively.

MAGNETIZATION, THERMOREMANENT, IN MINERALS 617

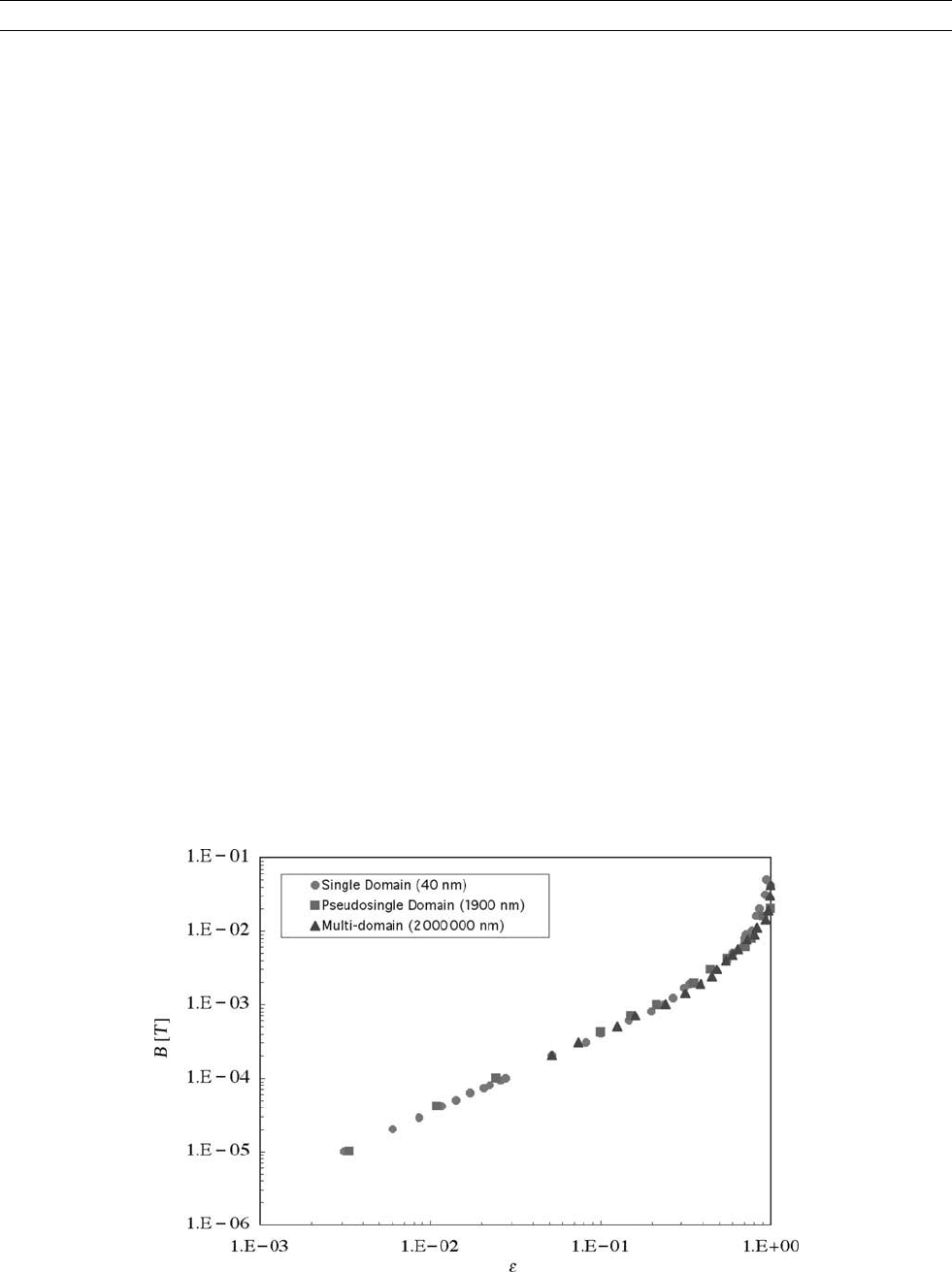
acquisitions performed using distinct magnetic materials (Kletetschka

et al., 2004): iron (Fe), iron-nickel (FeNi), magnetite (Fe

), hematite

(a-Fe

), and resistance wires MWS-294R and ALLOY52. Figure

M135 shows the field B required to reach efficiency E(T

) of the M

)

acquisition for equidimensional samples and a literature sample of aci-

cular magnetite (Dunlop and Argyle, 1997) in which the crystals are

highly elongated parallel to the applied field. Data near and at satura-

tion, where the simple power law breaks down (see Figure M136),

were excluded from the data set. The data set includes literature data

for pyrrhotite (Dekkers, 1989). Remarkably, each mineral is restricted

to its own line with the unit slope in the logB-logE space. Another

important feature reported in Kletetschka et al. (2004) is that the larger

the J

) (see legend) the larger the field B required to achieve a pre-

defined efficiency level E.

An increase of the minerals’ J

) is equivalent to a similar increase

in opposing demagnetizing field H

) (Dunlop and Özdemir, 1997;

Kletetschka et al., 2000b, c; Dunlop and Kletetschka, 2001) as well

as critical fields B requiring material to reach the saturation magnetiza-

tion at T

. The demagnetizing field at saturation relates to B

above which the energy minima become unstable causing the magnetic

moment to irreversibly rotate in an absence of thermal fluctuations.

Low J

) value is associated with low value of both B

) and H

and leads to a large critical SD size and large magnetic domain wall

spacing while large J

) implies large B

) (or H

) causing a fine

scale of the individual domains. Other effects, like magnetostriction,

anisotropy, and exchange constants, may also cause changes in the

overall magnetic domain size.

Data in Figure M135 are representative of multidomain (MD)

magnetic materials (1 mm grain size). However, the M

) varies with

the grain size according to the domain type (Kletetschka et al., 2004).

For example, MD magnetite has M

) that increases with decreasing

grain size (Dunlop, 1990). Similar grain size dependence has been

observed at saturation for J

) (Dunlop, 1990) (E ¼1). Thus, efficiency

E(T

)ofM

) rather than just M

) reduces the grain size dependence

to a minimum, and a line separation in the logB-logE plot can be used to

identify the magnetic mineralogy in ideal circumstances.

The insensitivity of the logB-logE(T

) plot to various grain sizes

is illustrated in Figure M135, where the M

) efficiency for SD

magnetite (literature data; Dunlop and Argyle, 1997) correlates with

MD magnetites; this breaks down when mineral size becomes so small

that it is near or in the superparamagnetic size range (Dunlop and

Argyle, 1997). The grain size independence is resolved in Figure

M136 where we have literature data of various M

) acquisitions

of titanomagnetite with disparate magnetic domain states identified

by the specific grain sizes (Dunlop and Waddington, 1975; Tucker

and O’Reilly, 1980; Özdemir and O’Reilly, 1982). Despite much

stronger M

) of fine vs large magnetic grains, all sizes appear to

have identical acquisitions when normalized by saturation remanence

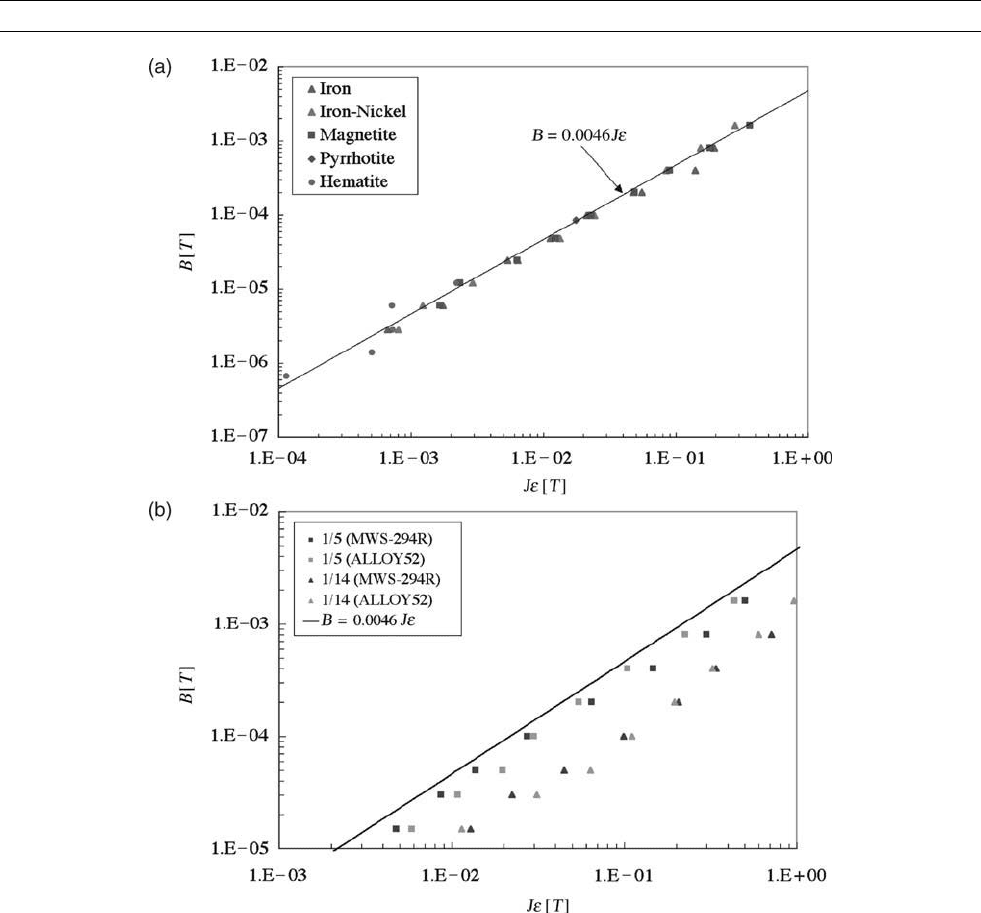
When neglecting effects near saturation (E < 0.3), this linear depen-

dence predicts approximate maximum values of the magnetic field

that can be recorded by a specific material (Figure M135). Near the

saturation, the magnetization is not linear with the applied field

(Figure M136) owing to Eq. (1) when E  1. Thus, the magnetic fields

at which E  1 should be the magnetic fields that define the values of

intrinsic B

) for the specific mineral. Knowledge of B

)fieldsin

principle can be used for dating of the magnetization according to

known magnetization viscous decay curves (Heller and Markert, 1973;

Borradaile, 1996). B

1 M

for shape anisotropy, B

/ l



for mag-

netoelastic anisotropy (Syono and Ishikawa, 1963b; Moskowitz, 1993)

(for n > 2) and B



for crystalline anisotropy (Syono and Ishi-

kawa, 1963a; Fletcher and O’Reilly, 1974) (for n > 8) where n is the

experimentally determined exponent. Both K and l go to zero much fas-

ter than M

when approaching Curie temperature T

.Energyminimum,

related to magnetic ordering, becomes shallower when approaching

due to thermal fluctuations (Stacey, 1958). Thus, for the purpose

of magnetic remanence blocking near T

we may consider only the

shape anisotropy: B

1 M

. The distribution of demagnetization field

vectors (tensors in general; Dunlop and Özdemir, 1997) relates to

), the nature of the resulting M

) and the E (T

) dependen-

cies. The B

) fields are small in minerals with low J

)causing

them to reach saturation (E(T

) ¼ 1) in much lower applied fields B

Figure M136 Acquisition fields are plotted against thermoremanent efficiency for contrasting domain states of titanomagnetite. Data for

multidomain and pseudosingle-domain mineral are from Tucker and O’Reilly (1980). Data for single-domain minerals are from

zdemir and O’Reilly (1982).

618 MAGNETIZATION, THERMOREMANENT, IN MINERALS

(Kletetschka et al., 2000c; Dunlop and Kletetschka, 2001). Larger

) in minerals with large J

) creates larger resistance against

acquisition of M

) and requires larger magnetizing fields to

achieve the saturation (E(T

) ¼ 1). For example, because magnetoelas-

tic and crystalline constants go to zero much faster than M

close to

, hematite has low B

) (due to shape anisotropy) at the point at

which TRM is acquired in contrast to its high B

at room tempera-

ture caused by high magnetoelastic anisotropy.

The fundamental role of J

) in mineral specific M

) acquisition

can be crystal clear by taking the data from Figure M135, multiplying

the magnetic efficiency E(T

)byJ(T

) ¼ m

)(Figure M137a).

Remarkably the resulting data set completely eliminates the effect of

the demagnetizing field during the M

) acquisition. Figure M137a

suggests that mineral M

) acquisitions can be in general approxi-

mated (linear regression coefficient R ¼ 0.97) by following a linear fit:

B ¼ aðTÞJ ðT ÞEðT

Þ; (Eq. 3)

where a ¼ (4.6  0.3)  10

3

with 95% confidence level for T ¼ T

300 K. The product J

)E(T

) is essentially the M

) normalized by

the squareness ratio J

)/J

) of the hysteresis loop. This linear beha-

vior (Figure M137a) indicates that all magnetic minerals should contri-

bute to a planetary thermoremanent magnetic anomaly (e.g., intense

magnetic anomalies detected on Mars (Acuña et al., 1999) with the same,

squareness J

)/J

)-normalized, M

) intensity. Because J

)

Figure M137 Magnetic acquisition fields are plotted against JE, which is the saturation magnetization J ¼ m

multiplied by efficiency

E of various materials at 300 K. (a) Equidimensional grains of iron, iron-nickel, magnetite, pyrrhotite, and hematite define a straight

line that is a result of a linear fit to all of the data. For J

at 300 K this fit has the form of B ¼ (4.6  0.3)  10

–3

JE. The linear

regression coefficient is R ¼ 0.97. (b) Effect of shape (nonequidimensional crystals) on thermoremanent acquisition fields for

wire materials (MWS-294R and ALLOY52) with small (1/5) and large (1/14) predefined length to diameter ratios compared with the

predicted acquisition (solid line) for equidimensional materials. Measurements were made with wires aligned parallel to the

applied field.

MAGNETIZATION, THERMOREMANENT, IN MINERALS 619

eliminates the mineral dependence observed in Figure M135 produced

byvariation in B

) in different minerals, B

) ¼ 0.23J

)in

Eq. (2) leads to the empirically observed relationship equation (3). Equa-

tion (3) breaks down if the Curie temperature of the magnetic material

gets near or below 300 K. With decreasing temperature, J

increases

and reaches a maximum at absolute zero temperature unless the material

undergoes a phase transition (e.g. Verwey transition for magnetite).

Extending the trend of the published J

(T) curves (Dunlop and Özdemir,

1997) into 0 K (ignoring any phase transitions) results in increase of J

by a factor of 1.05 for iron, 1.00 for hematite, 1.10 for magnetite, and

1.25 for pyrrhotite. This change of J

values has a negligible effect

on Eq. (3) and still results in a near perfect linear relationship where

a ¼ (4.2  0.3)  10

–3

with 95% confidence level for T¼T

¼0 K and

) ¼ 0.21J(T

). Using magnetic constants at absolute zero tempera-

ture, the problem of Curie temperature is eliminated and Eq. (3) can be

applied for any magnetic material.

As the microcoercivity B

) modifies the M

) acquisition, the

shape, magnetostriction, and crystalline anisotropy of the carriers

should have significant influence on the M

) acquisition curves.

For example, the length vs diameter ratio of the carrier should reduce

or increase the effect of B

) or the demagnetizing field (Dunlop and

Özdemir, 1997) for sample lengths parallel or perpendicular to the

field and thus shift the M

) acquisitions into lower or higher field

intensities, respectively. In Figure M135, M

) acquisition for acicu-

lar (elongated crystals parallel to the applied field) magnetite (Dunlop

and West, 1969) with diameter to length ratio 1:7 violates the equidi-

mensionality assumption. Although the data are for magnetic fields

near saturation of the magnetite, the demagnetizing field due to elon-

gation causes these grains to acquire magnetization at lower fields than

equidimensional magnetite grains. This shape effect was verified

experimentally (Kletetschka et al., 2004) by measuring M

) acquisi-

tion in industrial wires (MWS-294R and ALLOY52) with length to

diameter ratios 1:5 and 1:14 (Figure M137b), where the longer wires,

parallel to the field, required lower fields to acquire the predicted

intensity of magnetization.

The effect of placing wires perpendicular to the applied field should

be equal and opposite to placing them parallel. Consequently for a

large number of randomly oriented, elongated grains (such as is fre-

quently the case in igneous rocks) E should follow the same relation-

ships as for the single equidimensional grains used in this study.

This makes the TRM relationship far more applicable to those who

study natural materials. However, this information would have to be

accompanied by the caveat that, for the relationship to hold for multi-

ple grains, the grains would have to be identical in size and composi-

tion (equal J

, J

, and M

It is important to emphasize that a substitution of E to Eq. (3)

B ¼ aðT

ÞJ

ðT

ðTÞ

(Eq. 4)

represents the first ever means to obtain a paleointensity determination

using measurable quantities that does not involve the comparison of

a TRM imparted in the lab with that acquired in nature. Practical con-

siderations may pose a serious hindrance to it ever being used as such

because the above equation would not be satisfied by bulk values and

natural grains, capable of retaining a remanence over geological time,

would be too small to be measured individually. Possible solutions

involve isolating and amassing grains with sufficiently similar proper-

ties, decomposition of bulk values using FORC diagrams, and so on to

satisfy the requirements of Eq. (4).

Gunther Kletetschka

Bibliography

Acuña, M.H., Connerney, J.E.P., Ness, N.F., Lin, R.P., Mitchell, D.,

Carlson, C.W., McFadden, J., Anderson, K.A., Rème, H.,

Mazelle, C., Vignes, D., Wasilewski, P., and Cloutier, P., 1999.

Global distribution of crustal magnetization discovered by the Mars

global surveyor MAG/ER experiment. Science, 284: 790–793.

Borradaile, G.J., 1996. An 1800-year archeological experiment in

remagnetization. Geophysical Research Letters, 23(13): 1585–1588.

Cisowski, S., and Fuller, M., 1986. Lunar paleointensities via the

IRMs normalization method and the early magnetic history of the

Moon. In Hartmann, W.K., Phillips, R.J., and Taylor, G.J. (eds.),

Origin of the Moon. Houston: Lunar and Planetary Institute, pp.

411–424.

Dekkers, M.J., 1989. Magnetic properties of natural pyrrhotite. II. High-

and low-temperature behavior of J

and TRM as a function of grain

size. Physics of the Earth and Planetary Interiors, 57:266–283.

Dunlop, D.J., 1990. Developments in rock magnetism. Reports on

Progress in Physics, 53: 707–792.

Dunlop, D.J., and Argyle, K.S., 1997. Thermoremanence, anhysteretic

remanence and susceptibility of submicron magnetites: nonlinear

field dependence and variation with grain size. Journal of Geophy-

sical Research-Solid Earth, 102(B9): 20,199 –20,210.

Dunlop, D.J., and Kletetschka, G., 2001. Multidomain hematite: a

source of planetary magnetic anomalies? Geophysical Research

Letters, 28(17): 3345–3348.

Dunlop, D.J., and Özdemir, Ö., 1997. Rock magnetism: fundamentals

and frontiers. In Edwards, D. (ed.), Cambridge Studies in Magnet-

ism, Vol. 3. Cambridge: Cambridge University Press, 573 pp.

Dunlop, D.J., and Waddington, E.D., 1975. Field-dependence of ther-

moremanent magnetization in igneous rocks. Earth and Planetary

Science Letters, 25(1): 11–25.

Dunlop, D., and West, G., 1969. An experimental evaluation of single-

domain theories. Reviews of Geophysics, 7: 709–757.

Everitt, C.W.F., 1962. Thermoremanent magnetization II: experiments

on multidomain grains. Philosophical Magazine, 7: 583–597.

Fletcher, E.J., and O’Reilly, W., 1974. Contribution of Fe

2þ

ions to the

magnetocrystalline anisotropy constant K

of Fe

3–x

(0 < x <

0.1). Journal of Physics C, 7: 171–178.

Hargraves, R.B., and Young, W.M., 1969. Source of stable remanent

magnetism in Lambertville diabase. American Journal of Science,

267: 1161–1177.

Heller, F., and Markert, H., 1973. Age of viscous remanent magnetiza-

tion of Hadrians wall (Northern-England). Geophysical Journal of

the Royal Astronomical Society, 31(4): 395–406.

Hoye, G.S., and Evans, M.E., Remanent magnetizations in oxidized

olivine. Geophysical Journal of the Roya l Astronomical Society,

41: 139–151.

Kletetschka, G., Taylor, P.T., Wasilewski, P.J., and Hill, H.G.M.,

2000a. The magnetic properties of aggregate polycrystalline dia-

mond: implication for carbonado petrogenesis. Earth and Plane-

tary Science Letters, 181(3): 279–290.

Kletetschka, G., Wasilewski, P.J., and Taylor, P.T., 2000b. Hema-

tite vs. magnetite as the signature for planetary magnetic anoma-

lies? Physics of the Earth and Planetary Interiors, 119(3–4):

259–267.

Kletetschka, G., Wasilewski, P.J., and Taylor, P.T., 2000c. Unique ther-

moremanent magnetization of multidomain sized hematite: impli-

cations for magnetic anomalies. Earth and Planetary Science

Letters, 176(3–4): 469–479.

Kletetschka, G., Wasilewski, P.J., and Taylor, P.T., 2002. The role of

hematite-ilmenite solid solution in the production of magnetic

anomalies in ground and satellite based data. Tectonophysics, 347

(1–3): 166–177.

Kletetschka, G., Acuna, M.H., Kohout, T., Wasilewski, P.J., and

Connerney, J.E.P., 2004. An empirical scaling law for acquisition

of thermoremanent magnetization. Earth and Planetary Science

Letters, 226(3–4): 521–528.

Moskowitz, B.M., 1993. High-temperature magnetostriction of magne-

tite and titanomagnetites. Journal of Geophysical Research, 98:

359–371.

620 MAGNETIZATION, THERMOREMANENT, IN MINERALS

Néel, L., 1949. Théorie du traînage magnétique des ferromagnétiques

en grains fins avec applications aux terres cuites. Annales de Géo-

physique, 5:99–136.

Néel, L., 1955. Some theoretical aspects of rock magnetism. Advances

in Physics, 4: 191–243.

Özdemir, Ö., and O’Reilly, W., 1982. An experimental study of the

intensity and stability of thermoremanent magnetization acquired by

synthetic monodomain titanomagnetite substituted by aluminium.

Geophysical Journal of the Royal Astronomical Society, 70:141–154.

Shcherbakova, V.V., Shcherbakov, V.P., and Heider, F., 2000. Proper-

ties of partial thermoremanent magnetization in pseudosingle

domain and multidomain magnetite grains. Journal of Geophysical

Research-Solid Earth, 105(B1): 767–781.

Stacey, F.D., 1958. Thermoremanent magnetization (TRM) of multido-

main grainsin igneous rocks. Philosophical Magazine, 3:1391–1401.

Stacey, F.D., 1963. The physical theory of rock magnetism. Advances

in Physics, 12:45–133.

Stacey, F.D., and Banerjee, S.K., 1974. The Physical Principles of

Rock Magnetism. Amsterdam: Elsevier, 195 pp.

Syono, Y., and Ishikawa, Y., 1963a. Magnetocrystalline anisotropy of

xFe

TiO

.(1–x)Fe

. Journal of the Physical Society of Japan,

18: 1230–1231.

Syono, Y., and Ishikawa, Y., 1963b. Magnetostriction constants of

xFe

TiO

.(1–x)Fe

. Journal of the Physical Society of Japan,

18: 1231–1232.

Tucker, P., and O’Reilly, W., 1980. The acquisition of thermoremanent

magnetization by multidomain single-crystal titanomagnetite. Geo-

physical Journal of the Royal Astronomical Society, 63:21–36.

Wasilewski, P.J., 1977. Magnetic and microstructural properties of

some lodestones. Physics of the Earth and Planetary Interiors,

15: 349–362.

Wasilewski, P.J., 1981. Magnetization of small iron-nickel spheres.

Physics of the Earth and Planetary Interiors, 26: 149–161.

Cross-references

Blocking Temperature

Crystalline Anisotropy

Curie Temperature

Demagnetization Field

Demagnetizing Energy

Empirical Law

Hematite

Iron

Iron-Nickel

Magnetic Ordering

Magnetite

Magnetoelastic Anisotropy

Microcoercivity

Multidomains (MD)

Mysterisis Loop

Natural Remanent Magnetization (NRM)

Néel Theory

Phase Transition

Pseudo Single Domain (PSD)

Pyrrhotite

Remanent Efficiency of Magnetization (REM)

Saturation Magnetization

Saturation Remanence

Shape Anisotropy

Single Domains (SD)

Squareness Ratio

Super Paramagnetic

Thermal Remanent Magnetization (TRM)

Titanomagnetite

Verwey Transition

Viscous Decay

MAGNETIZATION, VISCOUS REMANENT (VRM)

Introduction

Viscous magnetization is the gradual change of magnetization with

time in an applied magnetic field H. Brief exposure of a ferromagnetic

material to a field results in isothermal remanent magnetization (IRM).

The additional remanence produced by a longer field exposure is vis-

cous remanent magnetization (VRM). The longer the exposure time

t, the stronger is the VRM.

Viscous remagnetization is the time-dependent change of VRM

or other remanences, such as thermoremanent magnetization (TRM),

depositional remanent magnetization (DRM), or chemical remanent

magnetization (CRM), in response to a change in the direction or

strength of H. In nature, such field changes are due to secular varia-

tion, excursions, polarity transitions, or plate motion. In laboratory

experiments, but never in nature, samples may be exposed to zero field

and the viscous decay of their magnetization measured.

The natural remanent magnetization (NRM) of rocks, sediments,

and soils usually includes a VRM produced at ambient temperature

by exposure to the weak (≲100 mT) Earth’ s magnetic field during

the Brunhes normal polarity epoch. This VRM obscures the useful

paleomagnetic information residing in older components of the NRM.

Removing the VRM is the purpose of standard “cleaning” procedures,

such as alternating field (AF) and thermal demagnetization.

Brunhes-epoch VRM is distinctive because it is roughly parallel to

the present-day local geomagnetic field. It is usually weaker than

TRM and DRM and also “softer” or more easily cleaned than these

older NRMs. However, magnetically “hard” or high-coercivity miner-

als like hematite, goethite, pyrrhotite, and some compositions of

titanomagnetites and titanohematites have hard VRM that is not easy

to AF demagnetize.

Rocks that have been exposed to the Earth’s field at elevated tempera-

turesfor long times acquire thermoviscous magnetization (TVRM), which

may replace part or all of their primary NRM. Usually these rocks are

slowly cooling plutons, or have been deeply buried in sedimentary basins,

volcanic piles, or mountain belts. TVRM blurs the distinction between

thermal processes like TRM and partial TRMs and time-dependent pro-

cesses like VRM and viscous remagnetization.

In reality, even ambient temperature is sufficiently high compared to

0 K that time t and temperature T are interwoven in VRM and viscous

overprinting. The fundamental mechanism of all viscous processes is

the slow, continuous approach of the magnetization M to its thermal

equilibrium value in field H at T, aided by thermal fluctuations of

the magnetization in each crystal. Fortunately, the approach to equili-

brium is usually extremely sluggish (hence viscous) at ordinary tem-

peratures. If this were not so, there would be no surviving NRM of

ancient origin, and no paleomagnetism or seafloor magnetic anomalies

to track plate tectonic movements.

Although most viscous magnetization changes are driven by thermal

fluctuations, another possible source of viscous effects is slow diffusion

of lattice defects that pin domain walls in multidomain crystals. This

diffusion after-effect is most significant in titanomagnetites over geologi-

cally short times (Moskowitz, 1985).

Theory of single-domain VRM

The Néel (1949, 1955) theory of time- and temperature-dependent

magnetization deals for simplicity with ensembles of N identical uni-

axial single-domain grains, all mutually aligned and having volume

V, anisotropy constant K(T), and spontaneous magnetization M

(T).

At time t ¼ 0, magnetic field H is applied parallel to the anisotropy

axis. At time t, n

grains have their moments þVM

in the direction

of H and n



grains have their moments –VM

opposite to H.

The distribution function n(t)/N ¼ (n

–n



)/N, which equals M(t)/M

obeys the kinetic equation

MAGNETIZATION, VISCOUS REMANENT (VRM) 621

dn=dt ¼½nðtÞn

=t; (Eq. 1)

where the equilibrium value n

/N ¼ tanh(VM

H/kT) and the relaxation

time t, due to thermal activation of moments over the energy barrier VK

due to anisotropy, is

1=t ¼ 2f

exp½VKðTÞ=kT; (Eq. 2)

with f

 10

10

1

At constant temperature, the solution to Eq. (1) is

nðtÞn

¼½nð0Þn

expðt=tÞ; (Eq. 3)

an exponential decay of the out-of-equilibrium distribution function

and magnetization. Néel introduced an approximation that replaces

the real exponential decay by a step function,

nðtÞ¼nð0Þ if t  t

nðtÞ¼n

if t > t: (Eq: 4)

In the case of TRM, where t changes rapidly with small changes in T,

Néel’s approximation leads to the definition of the blocking temperature

, at which the ensemble rapidly passes from a thermal equilibrium

state to an out-of-equilibrium state during cooling, or the reverse during

heating, e.g., in thermal demagnetization. The blocking concept is less

useful in isothermal viscous magnetization because t remains constant

and all changes are a result of changing t.

Any real sample contains many ensembles with different values of V

and K. The grain distribution f (V, K)dV dK is generally poorly deter-

mined, but the formal solution of Eq. (3) for acquisition of magnetic

moment m(t) by all ensembles, starting from a demagnetized state, is

mðtÞ¼

½1  expðt=tÞ f ðV ; KÞdV dK: (Eq. 5)

Numerical solutions can be found for specified forms of f (V, K).

Time and temperature de pendence of VRM

If f (V, K) is constant or nearly constant over a range of (V, K), the con-

volution of the exponential time dependence for a single ensemble

(Eq. (3)) with f (V, K), as expressed by Eq. (5), leads to a logarithmic

dependence of m(t)ont (see Dunlop, 1973, or Dunlop and Özdemir,

1997, Chapter 10 for details). Experimentally most ferromagnetic

materials on a laboratory timescale exhibit viscous changes that are

indeed approximately proportional to logt. Figure M138 illustrates

the measured time dependence of VRM for oxidized and unoxidized

pyroclastics on a t scale from 15 min to 28 days (about 4 decades of

t). Only a limited range of (V, K) is activated in a few decades of t

and the VRM increases more or less linearly on a logt scale.

According to Eq. (2), for T constant, VK is proportional to log2f

Using Néel’s blocking approximation (4), it is then possible to trans-

form f (V, K) directly into the corresponding distribution g(logt). In this

way, one can predict the viscosity coefficient S ¼ @M /@logt for a sam-

ple whose grain distribution f (V, K)isknown.

Another approach (Walton, 1980) is to calculate S directly from

Eq. (5) without explicitly invoking a blocking approximation. If we

replace K by a suitable average value and approximate n

/N by

H/kT, since H is small, we find

S ¼

ðM

H=kTÞðt=tÞ½1  expðt=tÞV

NfðV ÞdV : (Eq. 6)

The integrand is of the form x(1–e

x

), with x itself exponential. It

peaks sharply at x ¼ 1ort ¼ t, which is in fact the blocking condition.

All nonexponential factors can be assigned their blocking values, e.g.,

V ! V

¼ (kT/K) log2f

t, and taken outside the integral, giving

S ¼ Ik

NðM

ÞHðlog 2f

tÞ

f ½kT=KÞlog 2f

t; (Eq. 7)

the integral I being approximately 1.

Assuming that the anisotropy is due to grain shape, so that K(T) /

ðTÞ, and that the grain distribution is uniform over the range of

ensembles affected in time t, we obtain

S ¼ CHðT=M

ðlog 2f

tÞ

; (Eq. 8)

whereas if f (V) / 1/V, as for the larger grains in a lognormal distribution,

S ¼ C

HðT=M

log 2f

t; (Eq. 9)

C, C

being constants. Either Eq. (8) or (9) predicts a logt dependence

for VRM intensity over times short enough that logt  log2f

 23.7,

i.e., for a few decades of t, as observed. Deviations from logt depen-

dence will become obvious even at short times for very viscous sam-

ples, which scan larger fractions of the grain distribution, and at

longer times for all samples. Deviations will appear earlier if Eq. (8)

applies rather than Eq. (9).

VRM of multidomain and interacting grains

Viscous magnetization due to thermal activation of domain walls has

been treated theoretically in the weak-field limit by Néel and in the

Figure M138 Viscous remanent magnetization measured after exposure times of 15 min to 4 weeks to a 200 mT field (data: Saito et al.,

2003). Upper curve, unoxidized pyroclastic sample containing large grains of titanomagnetite. Lower curve, oxidized pyroclastic

containing hematite and titanohematite.

622 MAGNETIZATION, VISCOUS REMANENT (VRM)

presence of self-demagnetizing fields by Stacey (see Dunlop, 1973, for

a review). All theories predict a logt dependence of VRM for

geologically short times. The viscosity coefficient S varies with tem-

perature as T/M

or (T/M

)

1/2

. The theories resemble single-domain

formulations with V in Eq. (2) replaced by the volume V

act

activated

in a single Barkhausen jump. The frequency constant f

is 10

10

1

, as for single-domain grains. Viscous magnetization due to activa-

tion of entire walls should be negligible because V

act

 V of a single-

domain grain. It must be that segments of walls are activated past single

pinning sites.

In nature, titanomagnetite and pyrrhotite crystals sometimes fail to

renucleate equilibrium domain structures following saturation, result-

ing from heating to the Curie temperature. A possible mechanism for

multidomain viscous magnetization is thermally activated nucleation

of domains in parts of the crystal where the internal field is close to

the critical nucleation field. This process has been termed transdomain

VRM. Nucleation events have been observed in magnetite during small

changes of T (Heider et al., 1988) but are not yet documented for

changing t at constant T.

Interacting single-domain grains have been approached in two dif-

ferent ways. One method is to treat them collectively by increasing

V from the single-grain value. This approach preserves the experimen-

tally observed logt behavior but it is not known at what level of inter-

action the picture breaks down. Another approach is to deal with

individual particles under the influence of a randomly varying interac-

tion field. Walton and Dunlop (1985) predicted deviation from logt

behavior when the interactions are strong. Their theory gave a good

fit to viscous magnetization data for an interacting single-domain

assemblage with known f (V).

Experimental results

Grain size dependence of viscosity coefficients

Room-temperature viscosity coefficients S have their highest values in

single-domain grains with volumes V just above the critical superpar-

amagnetic volume V

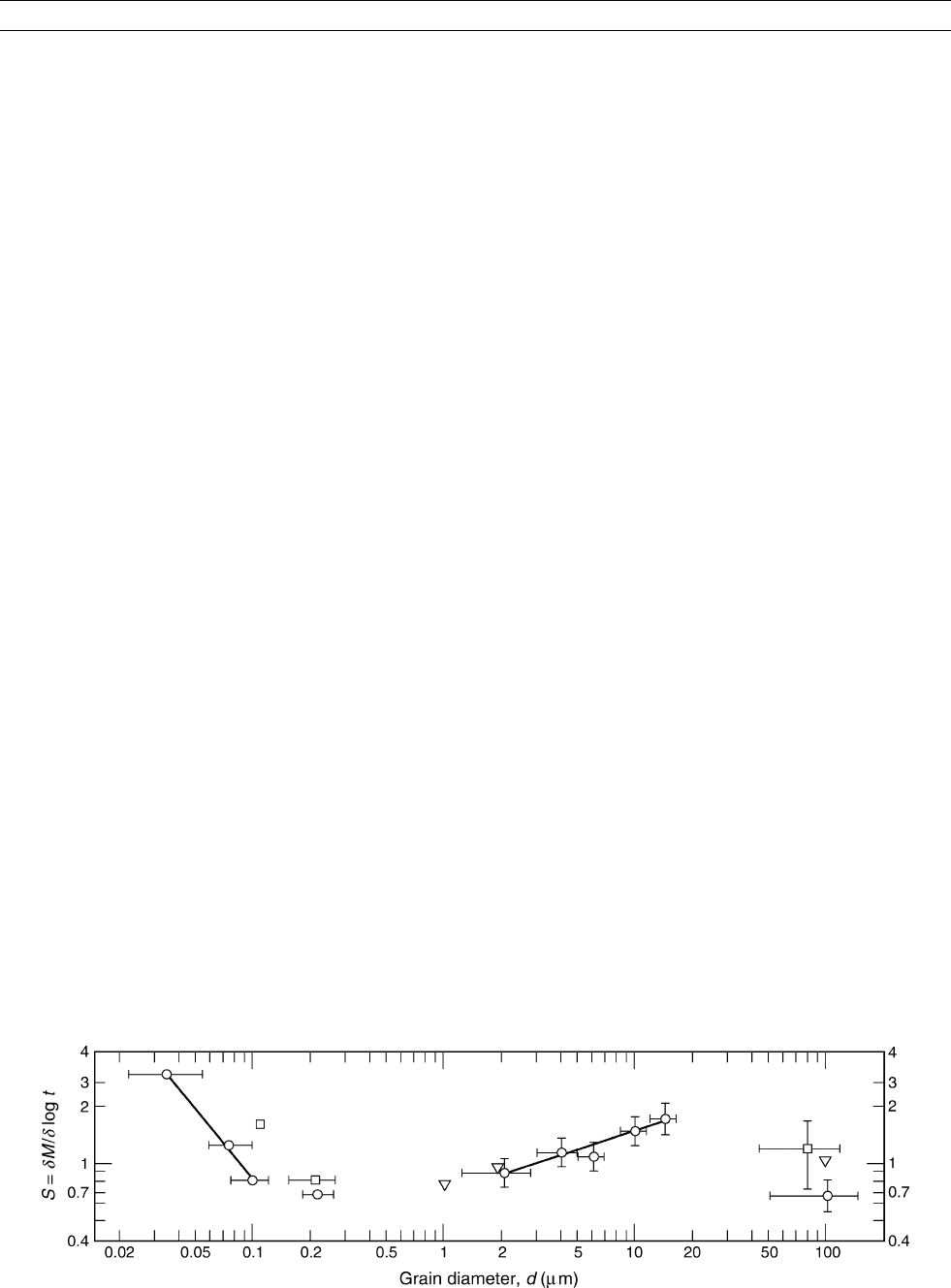
. Figure M139 illustrates the data for magnetite.

Data sets for other minerals are even smaller. Between the magnetite

critical superparamagnetic size (0.025–0.03 mm) and the maximum

size for single-domain behavior (0.07–0.08 mm), S decreases by at

least a factor 4. The decrease may actually be larger and more precipitous

than shown. Even in carefully sized samples, there is always a fraction of

very fine grains. This fine fraction probably controls the short-term vis-

cous behavior, because, according to Eqs. (2) and (4), only grains with

very small V will be activated in the short times used in laboratory

experiments. Similar “contaminating” ultrafine grains may explain the

constant baseline value of S in grains larger than single-domain size.

The twofold increase in S over the upper pseudosingle-domain

region (2–15 mm) is probably real and due to the increasing ease with

which segments of walls can escape from their pins as the scale

of the domains grows. On the other hand, large multidomain grains

80–100 mm in mean size have significantly lower S values.

In summary, strong viscous magnetization is found mainly in the

finest single-domain grains. However, small multidomain (so-called

pseudosingle-domain) grains are also significantly viscous.

Observations on lunar rocks and soils (see Dunlop, 1973 and

Dunlop and Özdemir, 1997, Chapter 17 for summaries) confirm this

trend. Lunar soils and loosely welded soil breccias containing nearly

superparamagnetic iron particles are among the most viscous materials

known, whereas crystalline rocks and mature breccias containing mul-

tidomain iron exhibit a consistent but small viscous magnetization.

The viscous nature of lunar samples greatly complicated the study of

their other magnetic properties during the Apollo missions.

Temperature dependence of viscous magnetization

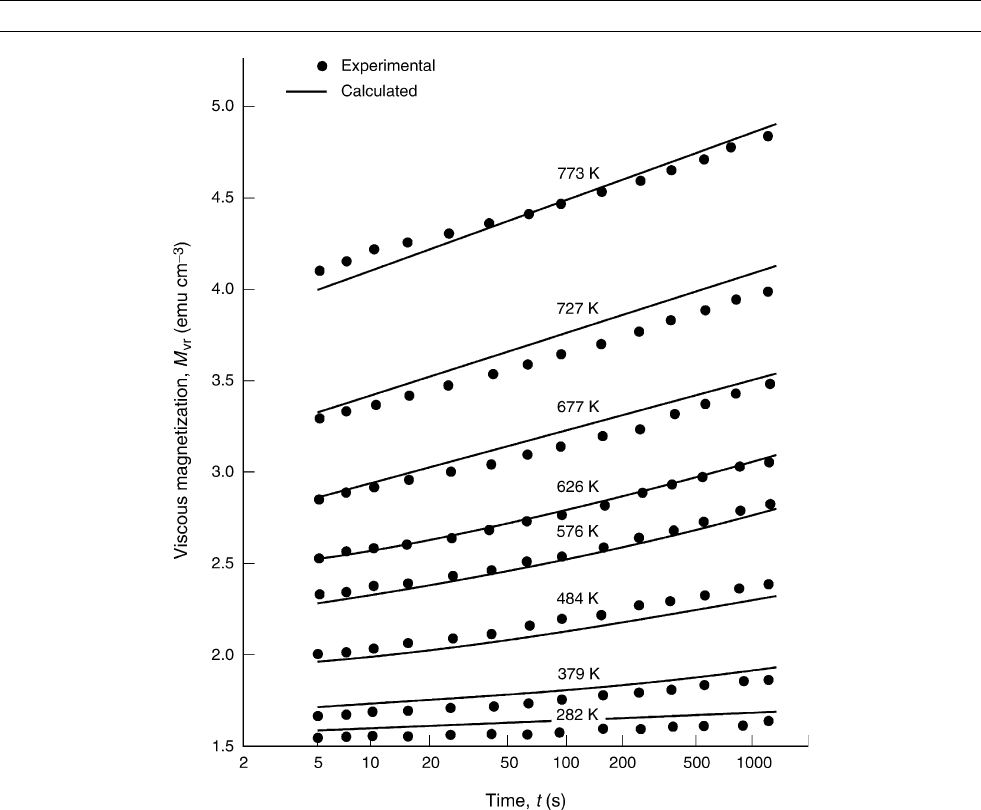
Viscous magnetization data for a single-domain magnetite sample

(mean grain size 0.037 mm) at and above room temperature appear

in Figure M140. Zeroing the field H for each measurement would have

changed the initial state for subsequent measurements. Therefore vis-

cous induced magnetization in the presence of H was measured.

Over the short time-spans examined (2.4 decades of t), M

is linear

in logt, as predicted by Eqs. (2), (8), and (9). The viscosity coefficient

S, the slope of each data run, increases steadily with increasing T. This

too is as predicted by theory. However, the inherent temperature

dependence of S,inEqs. (8) and (9) for example, tends to be obscured

by the variability of the grain distribution f (V, K), which is scanned with

a narrow thermal “window,” as expressed by the factor f (kT/K)log2f

in Eq. (7).

Very different temperature dependences of viscous magnetization

have been reported for magnetite and titanomagnetites of various grain

sizes by different authors. In many cases, the higher-T results are dis-

tinctly nonlinear in logt. However, a good theoretical match is evident

in Figure M140 between the single-domain magnetite data (Dunlop,

1983) and the theory of equations (6)–(9), using the measured f (V)

of this sample (Walton, 1983).

Field dependence of viscous magnetization

Experiments confirm the theoretical prediction (e.g., Eqs. (6)–(9)) that

VRM intensity is proportional to field strength H for weak fields. The most

detailed studies are those of Creer (1957) on single-domain hematite and

Le Borgne (1960) on soils containing single-domain magnetite and

maghemite. Linear behavior was observed for 0.05 mT  H  1mT.

Figure M139 Viscosity coefficients S for sized grains of magnetite. Data: triangles, Shimizu (1960); circles, Dunlop (1983); squares,

Tivey and Johnson (1984).

MAGNETIZATION, VISCOUS REMANENT (VRM) 623

Viscous magnetization at short times: frequency

dependent and quadrature susceptibility

Viscous changes in magnetization can be detected over very short

times by measuring initial susceptibility w (short-term induced M, nor-

malized by H) as a function of the frequency f of an alternating field

(AF)

H. In effect, each cycle of the AF restarts the viscous magnetiza-

tion experiment. A second method is to measure the quadrature (90



out-of-phase) component of susceptibility w

, which represents a

time-delayed response to

In the classic experiments of Mullins and Tite (1973) on soils containing

single-domain size magnetite and maghemite, @w/@logf and w

were con-

stant over the tested range of f (66–900 Hz, 1.4 decades of t). No frequency

dependence or quadrature susceptibility was detected for multidomain

magnetite.

A pair of measurements of w at two standard frequencies is routinely

used in environmental magnetic studies as a test for the presence of

nearly superparamagnetic magnetite or maghemite. Because the fre-

quencies are preset, there is no attempt to tune the viscosity measure-

ment to other minerals or to domain states other than single-domain.

Much more granulometric information could be obtained with a little

extra effort by scanning a wider range of f and by extending the

measurements to temperatures other than room temperature

(e.g., Jackson and Worm, 2001).

Demagnetizing VRM

AF demagnetization

The AFs

H used in frequency-dependent susceptibility measurements

have small amplitudes, usually 0.1 mT, and do not seriously modify

preexisting remanences. If larger AFs are applied, they entrain single-

domain moments or domain walls, causing them to oscillate and

destroy VRM (or any other remanence, for sufficiently large

H). To

demagnetize a previously magnetized sample,

H is slowly decreased

from its maximum value at a rate f, leaving about equal numbers of

moments or domains in one or the other polarity. AF demagnetization

is carried out in a stepwise fashion. The maximum field is increased

in steps, starting from small values, so as to gradually erase remanence

components of increasing AF coercivity.

VRM is often the NRM component of lowest coercivity and there-

fore erased first. Indeed the strategy of AF cleaning in paleomagnetism

is firmly rooted in this assumption.

Figure M140 Viscous magnetization of a single-domain magnetite sample (mean grain size 0.037 mm) at various temperatures.

Dots: measured results, Dunlop (1983); lines: theoretical fits, Walton (1983).

624 MAGNETIZATION, VISCOUS REMANENT (VRM)

Strong fields lower the energy barrier VK to rotation of single-domain

moments or the corresponding “barrier” (pinning energy) for domain

wall motion. In the single-domain case, Eq. (2) is modified to

1=t

¼ f

exp½ðVKðTÞ=kTÞð1  M

H=2KÞ

: (Eq. 10)

One consequence is hard VRM in minerals with high K/M

, like

hematite, goethite, pyrrhotite, elongated single-domain iron, and

many compositions of titanomagnetite, titanomaghemite, and titanohe-

matite. VRM is produced by a weak field and Eq. (2) applies, but it

is demagnetized by a strong field

H for which Eq. (10) is

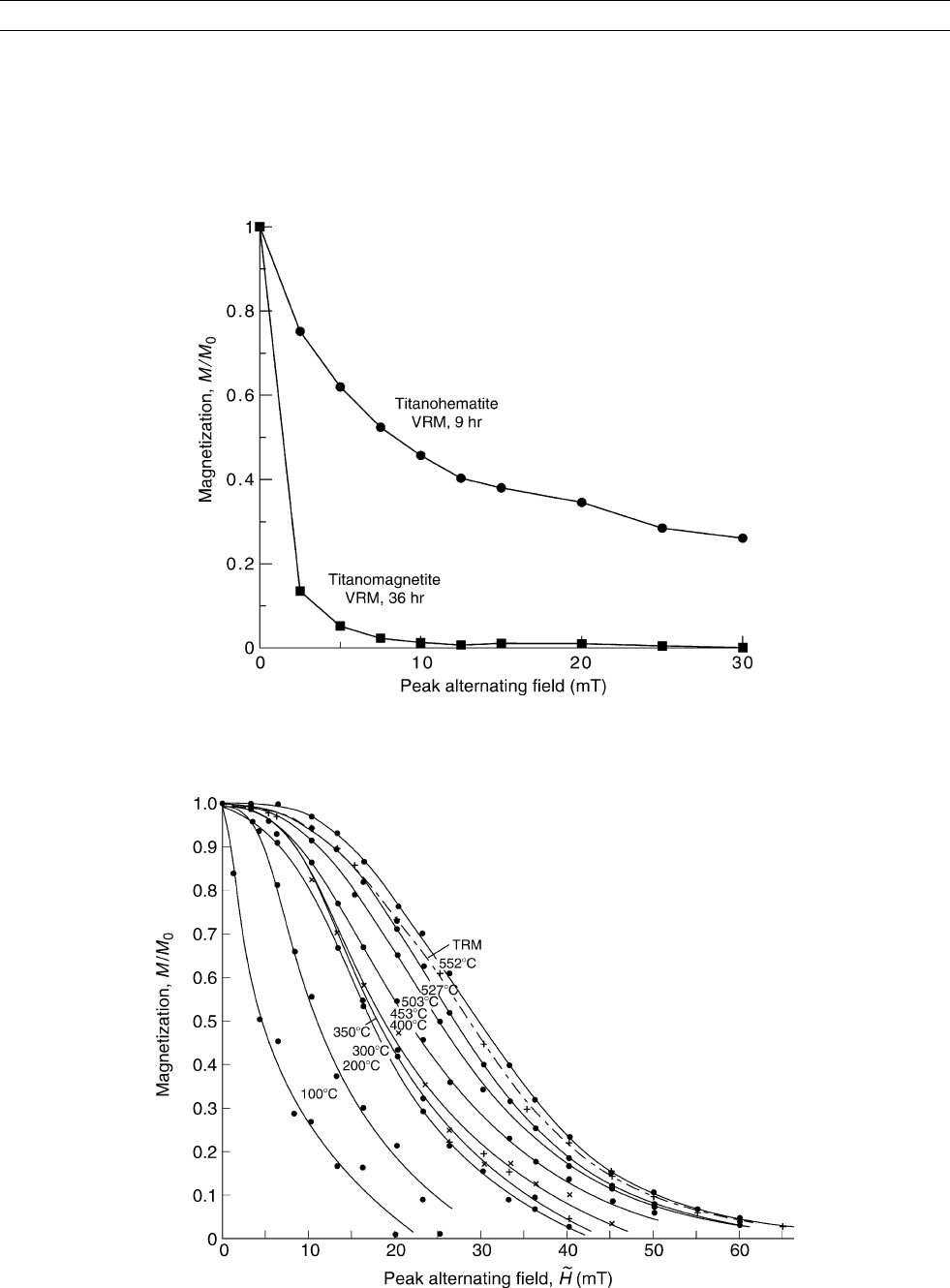
Figure M141 AF demagnetization of some of the VRMs of Figure M138 (data: Saito et al., 2003). VRM of the unoxidized

titanomagnetite is erased by 2.5 mT. VRM of the oxidized sample containing titanohematite is much more resistant.

Figure M142 AF demagnetization of VRMs produced by 2.5 h exposure to a 50 mT field at the temperatures shown (after Dunlop and

zdemir, 1990). VRMs produced at higher temperatures are increasingly resistant to AF cleaning.

MAGNETIZATION, VISCOUS REMANENT (VRM) 625