Gubbins D., Herrero-Bervera E. Encyclopedia of Geomagnetism and Paleomagnetism

Подождите немного. Документ загружается.

appropriate. Using the blocking approximations t ¼ t for the last

ensemble to acquire VRM and t

¼ 1/f when H ¼

H for AF cleaning

of this same ensemble, we have by combining (2) and (10),

H ¼ð2K=M

Þ½1 ðlog f

=f Þ

1=2

=ðlog 2f

tÞ

1=2

: (Eq. 11)

The resistance of VRM to AF cleaning is thus proportional to K/M

the other factor being independent of mineral properties.

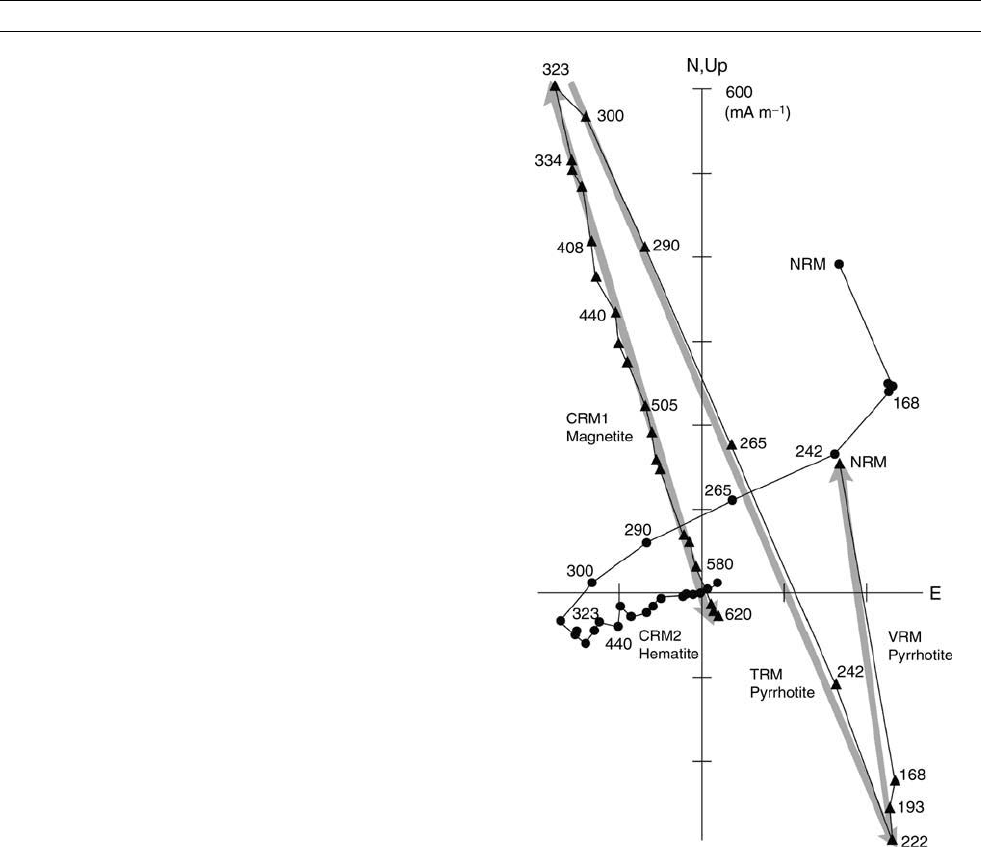
Figure M141 confirms this prediction. One sample is an unoxidized

pyroclastic containing iron-rich titanomagnetite with low coercivity

K/M

. VRMs produced over all ranges of t are very soft, demagnetizing

almost completely for

H ¼ 2.5 mT. The other sample is oxidized and

its VRM is carried by titanohematite of much higher coercivity. VRMs

for this sample are more resistant to AF demagnetization, surviving to

H ¼ 10–20 mT. This is only a moderately hard VRM, because in fact

both these samples contain multidomain-size grains, not single-domain

material to which Eq. (11) strictly applies. However, practically any

rock whose NRM is due mainly to hematite has VRM that cannot be

entirely removed by

H ¼ 100 mT (Biquand and Prévot, 1971).

VRM produced in nature at above-ambient temperature and subse-

quently AF cleaned at room temperature is also relatively hard.

Figure M142 shows an example for a single-domain magnetite sample

that was given VRMs in 2.5 h runs at temperatures as high as 552



(the Curie point is 580



C). The effect of T is to shift the window of

f (V, K) affected viscously in t ¼ 2.5 h to grains with increasingly high

K (see Dunlop and Özdemir, 1997, Chapter 10).

Ambient-temperature VRM in magnetically hard minerals and ele-

vated-temperature VRM in both hard and soft minerals are both diffi-

cult to remove completely or cleanly (without removing part of the

primary NRM as well) by AF demagnetization. A more satisfactory

method is thermal demagnetization.

Thermal demagnetization

Because VRM is a thermoviscous relaxation phenomenon, thermal

demagnetization should be the most efficient way of erasing VRM.

Randomizing single-domain moments or domain wall positions is

accomplished by random thermal excitations, resulting in a truly demag-

netized state, not the polarized condition that follows AF cleaning. From

Eq. (2), the laboratory temperature T

to which a single-domain sample

must be heated (in zero field) on a timescale t

(typically an hour or less)

to erase VRM produced over a long time t

in nature at temperature T

is given by

log 2 f

ðT

Þ¼T

log 2f

ðT

Þ; (Eq. 12)

(Pullaiah et al., 1975), assuming K(T) / M

ðTÞ as for shape anisotropy.

Substituting t

¼0.78 Ma for VRM acquired over the Brunhes epoch

at surface temperatures, one obtains for magnetite T

 250



C. This is

indeed the typical reheating temperature needed to completely erase

magnetite VRM, although AF cleaning often serves very well in this

case. For pyrrhotite, with a different Curie temperature (320



C) and

(T) variation, the corresponding T

is  130



Figure M143 illustrates how complete erasure of VRM is detected.

The NRM vector of this sample (Milton Monzonite, SE Australia),

plotted in vector projection, reveals four components whose removal

requires successively higher heatings. The VRM, produced by the

Earth’s field over 100 ka at  165



C (Dunlop et al., 2000), and

the primary TRM are carried by single-domain pyrrhotite, the two

CRMs by magnetite and hematite. The junction between the VRM

and TRM vectors is sharp because single-domain thermoviscous rema-

nences separate cleanly in heating. The vector direction changes

abruptly at the junction temperature because the TRM was produced

by a reverse-polarity field and the VRM by a normal-polarity field.

The junction temperature T

is >130



C because T

was above ambi-

ent while the rock was buried and VRM was being produced. Using

¼ 100 ka, T

¼ 165



C, and M

(T) for pyrrhotite in Eq. (12) yields

¼ 222



C, as observed.

Contours of constant (V, K) are often plotted on a time-temperature

diagram (Pullaiah et al., 1975), which can then be used as a nomogram

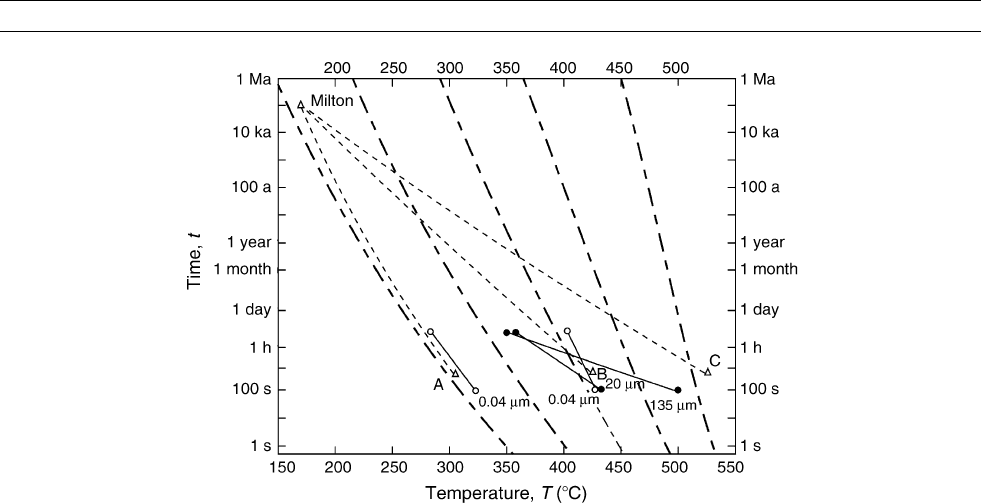
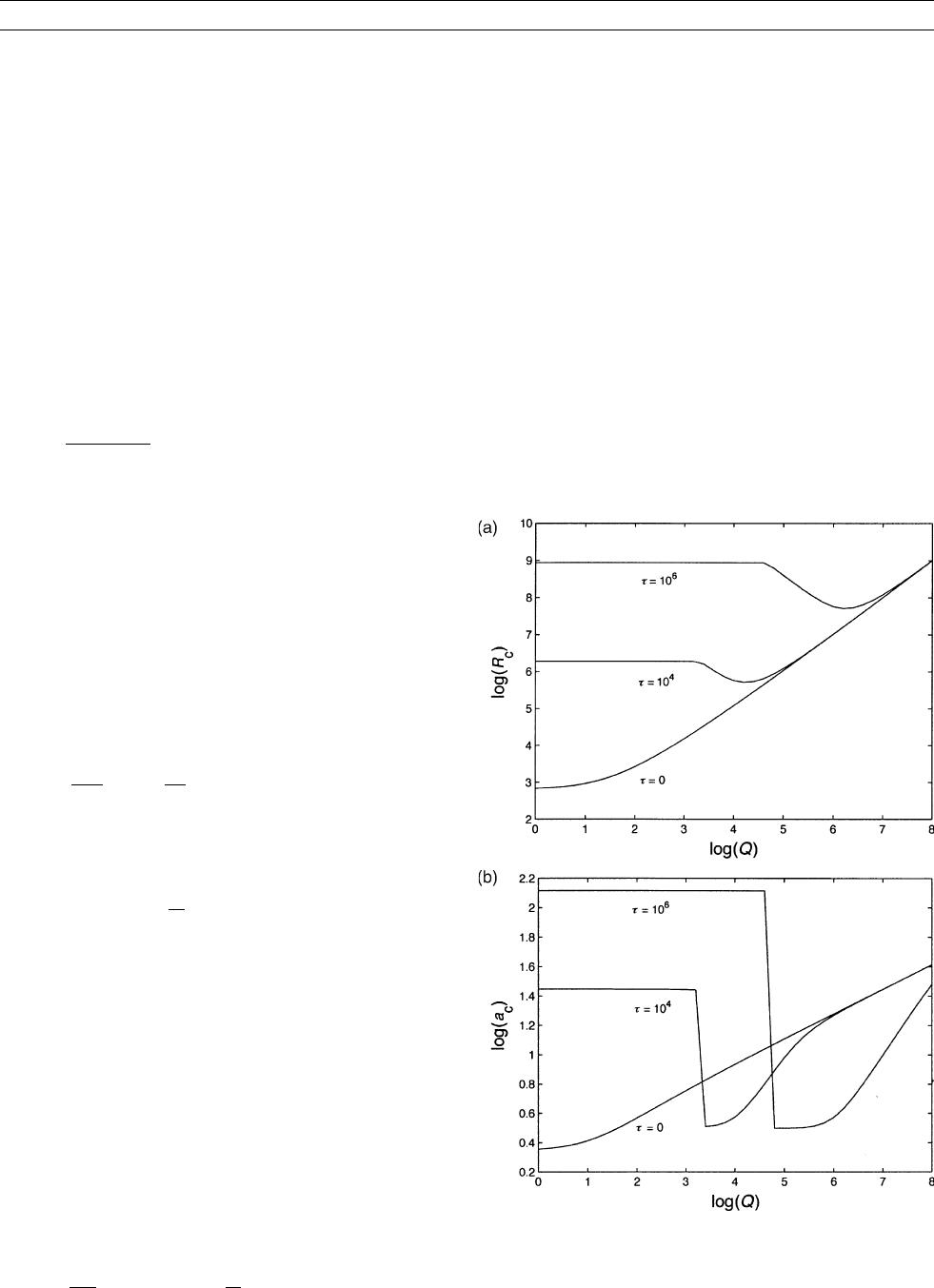
for locating matching (T, t) pairs. Figure M144 is such a diagram, with

contours for magnetite based on Eq. (12). It is clear from the data

plotted, some of which are from the Milton Monzonite, that single-

domain magnetite samples (0.04 m m, A) obey Eq. (12) but samples with

pseudosingle-domain (20 mm, B) and multidomain (135 mm, C) magne-

tites follow contours with smaller slopes. That is, these latter grains

require more heating to remove their VRMs than the single-domain

theory predicts.

Observations of “anomalously high” unblocking temperatures in

thermal demagnetization of VRM are well documented in the litera-

ture. Initially it seemed possible to reconcile the data by using the

Walton (1980) single-domain theory outlined in an earlier section.

From Eq. (9),

Figure M143 Thermal demagnetization of NRM of a sample of the

Milton Monzonite (after Dunlop et al., 1997). The

pyrrhotite primary TRM and VRM separate cleanly in thermal

demagnetization to 222



C. Triangles and circles: vertical- and

horizontal-plane vector projections, respectively.

626 MAGNETIZATION, VISCOUS REMANENT (VRM)

ðlog 2f

ðT

Þ¼T

ðlog 2f

ðT

Þ; (Eq. 13)

which produces shallower contours resembling the trend of some of

the deviant data (Middleton and Schmidt, 1982).

However, on reflection it became clear that Eqs. (12) and (13) actu-

ally answer different questions (Enkin and Dunlop, 1988). Equation

(13) tells us what exposure time t

to field H at temperature T

will

produce the same VRM intensity as the original exposure to H for time

at T

. The question that is relevant to erasure of VRM by thermal

demagnetization, and is answered by Eq. (12), is what exposure t

H at T

will reactivate the same ensembles (V, K) as the exposure in

nature to H for time t

at T

. Because VRM intensity increases with

rising T even if f (V, K) is constant (e.g., Eq. (7)), the two answers will

always be different.

This has now been shown beyond doubt by the experiments of

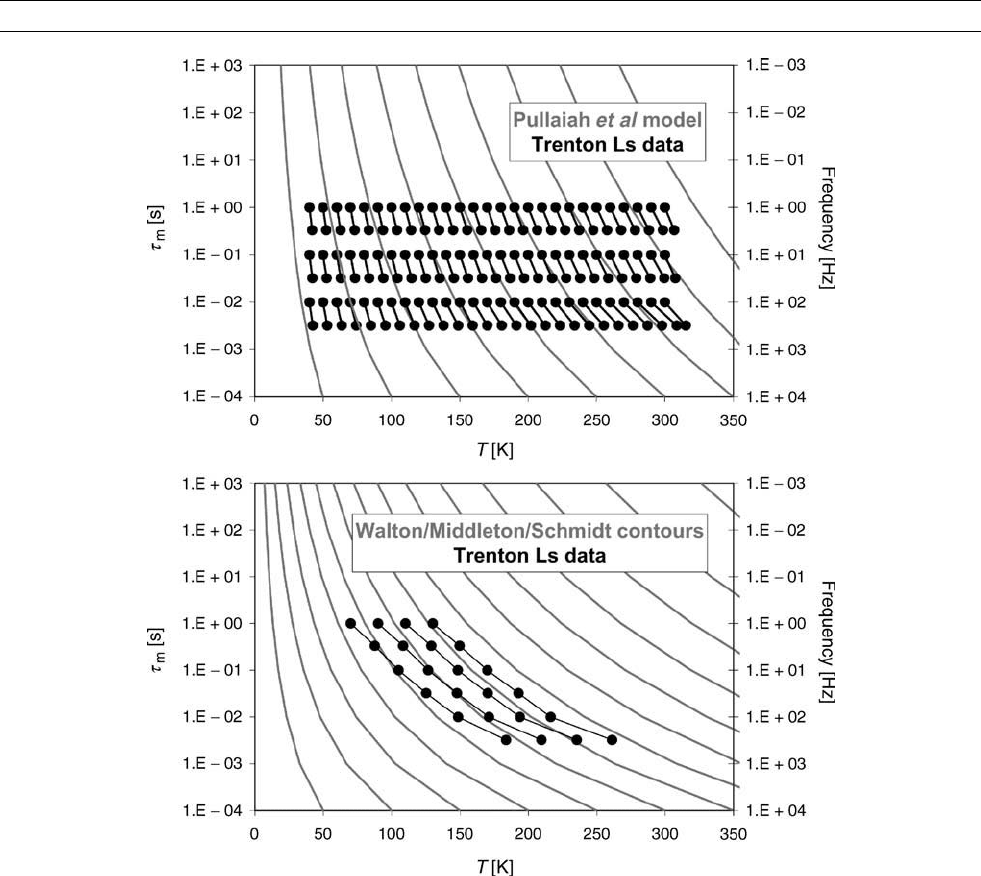
Jackson and Worm (2001), shown in Figure M145. They carried out

experiments on the magnetite-bearing Trenton Limestone below room

temperature at fixed, very short times t and varied T to either achieve

unblocking of the same (V, K) ensembles (upper graph) or produce the

same viscous magnetization intensity (lower). The former data sets

agree well with the Pullaiah et al. (1975) contours from Eq. (12), while

the latter are close to the predicted Walton-Middleton-Schmidt con-

tours from Eq. (13).

Discrepancies between the predictions of Eq. (12) and thermal

demagnetization results for rocks are mainly attributable to VRMs of

grains larger than single-domain size. The larger the grain size, the

greater the discrepancy, as illustrated by Figure M144. It is well

known that the Thellier (1938) law of independence of partial TRMs

is increasingly violated as grain size increases. One manifestation of

this violation is that partial TRMs produced over narrow T intervals

do not demagnetize over the same intervals, so that a clean separation

of partial TRMs is no longer possible using thermal demagnetization.

VRMs behave analogously. The average demagnetization tempera-

ture of both VRMs and partial TRMs is close to that predicted by

Eq. (12) (Dunlop and Özdemir, 2000) but domain walls continue to

move toward a demagnetized state at higher T, producing a “tail”

of unblocking temperatures. Unfortunately only the ultimate highest

unblocking temperature is easily detected experimentally, and it is

not predictable by any current theory.

To further complicate matters, the initial state of a multidomain

grain can strongly affect its magnetic behavior, including thermal

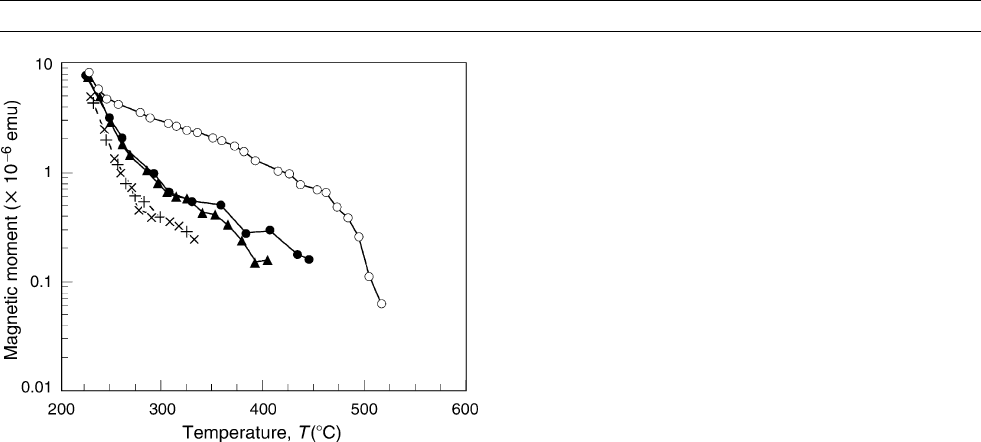
demagnetization. Figure M146 demonstrates that VRMs produced in

an AF demagnetized sample or in one thermally demagnetized and

then heated in a zero field to the VRM production temperature are sub-

sequently erased by further heating of 100



C. But a sample cooled in

a zero field directly from the Curie point to the VRM temperature

acquires a VRM that requires 250



C of further heating to remove.

These experiments use continuous thermal demagnetization, which

differs from standard stepwise demagnetization by not revisiting room

temperature for each measurement. Although these results may not

be directly applicable to standard paleomagnetic practice, they do

make the point that any multidomain sample retains a memory of its

entire past history and this may influence its later behavior in as yet

unpredictable ways.

Applications of viscous magnetization

Magnetic granulometry

Viscous magnetization is a sensitive probe of narrow (V, K) bands of

the grain distribution. If K has a narrow spread compared with V,

inversion of Eq. (5) by Laplace transforms yields f (t), i.e., f (V). A cru-

der estimate, which is adequate in most cases, is to use a blocking

approximation as in Eq. (7) to obtain f (V

) ¼ f (kTlog2f

t/K). Small

can be accessed by using the frequency dependence of w. Large

can be activated in VRM experiments above room temperature.

Estimating Brunhes-chron VRM

In very viscous rocks, particularly unoriented or partially oriented sea-

floor samples, one would like to know if a large part of the NRM is

Figure M144 Theoretical time-temperature contours based on Eq. (12) compared to data from thermal demagnetization of

VRMs produced at elevated temperatures for synthetic magnetites and samples of the Milton Monzonite (after Dunlop and O

zdemir,

2000). Single-domain samples agree well with the contours. Larger pseudosingle-domain and multidomain samples are more difficult

to demagnetize than predicted.

MAGNETIZATION, VISCOUS REMANENT (VRM) 627

VRM produced during the Brunhes chron (the past 0.78 Ma). For sam-

ples magnetized during an earlier normal-polarity chron, there is not

much difference between the directions of primary TRM and recent

VRM. No sharp junctions like those of Figure M143 appear in thermal

demagnetization trajectories.

Since relaxation times of 1 Ma are inaccessible in laboratory

experiments, two different methods have been used. First is simple

extrapolation of laboratory data, assuming S remains constant over

many decades of t beyond the laboratory scale. This is certainly unjus-

tified with the more viscous shallow oceanic rocks, e.g., doleritic flows

(Lowrie and Kent, 1978). With less viscous rocks, like those of

Figure M138, simple extrapolation implies that a substantial part of

the NRM could be VRM, but a precise quantitative estimate is not

possible (Saito et al., 2003).

The second method is to activate long relaxation times in the labora-

tory in mild heatings above room temperature. For titanomagnetite of

mid-ocean ridge compositions, the heatings must remain below the

Curie point (150–200



C). Another criterion is that chemical alteration

must be prevented. Thermal demagnetization of the NRM, using

Eq. (12) or Figure M144 as a guide to the (T

, t

) combination needed,

is a better approach than production of a new VRM. In the latter

experiment it is not possible to reactivate at T

all the ensembles

(V, K) that carried the room-temperature VRM.

Paleothermometry

If the approximate residence time t

over which VRM was acquired

can be estimated (within about an order of magnitude, since log t

involved), but the burial temperature during VRM production is

unknown, Eq. (12) or Figure M144 can again be used to analyze

laboratory thermal demagnetization data and estimate T

. This method

is useful for estimating depth of burial in a sedimentary basin as a

guide to hydrocarbon potential. It of course only works well if the

VRM has single-domain carriers. A recent variant, which is capable

Figure M145 Comparison of equivalent (t, T) sets determined from frequency-dependent susceptibility data at low temperatures for the

magnetite-bearing Trenton Limestone (after Jackson and Worm, 2001). The upper data compare reactivation of equivalent grain

ensembles (V, K) and are in good agreement with Eq. (12). The lower data compare equal viscosity coefficients at different T and agree

reasonably well with Eq. (13).

628 MAGNETIZATION, VISCOUS REMANENT (VRM)

in principle of estimating both t

and T

independently, is to analyze

thermal demagnetization data for VRMs carried by two minerals,

e.g., magnetite and pyrrhotite (Dunlop et al., 2000).

Cooling-rate dependence of TRM

Another thermoviscous effect is the variation of TRM intensity

depending on cooling rate. For single-domain grains, about 5%

increase in intensity is predicted for the slowest versus the fastest prac-

tical laboratory cooling rates. The theory is not simple because T and t

vary simultaneously but the few experimental data that exist agree

quite well with predictions (Fox and Aitken, 1980). There is some evi-

dence that for multidomain grains, TRM intensity may decrease for

slower cooling (Perrin, 1998). The enormous range of cooling rates

present in nature when metamorphic terrains are uplifted over millions

or tens of millions of years by erosional unroofing may lead to much

larger changes than can be measured in the laboratory. So far no

method of simulating or estimating changes over these very long time-

scales has been proposed.

VRM as an archeological dating tool

When blocks of stone were reoriented in building historical or more

ancient structures, viscous remagnetization of their NRMs began. This

“clock” is less than ideal because the changes in M are roughly in pro-

portion to logt, so that the resolution dM/dt ¼ t

1

dM/dlogt ¼ S/t

decreases with increasing age. The classic study by Heller and Markert

(1973) found reasonable values, 1.6–1.8 ka, for the age of Hadrian’s

Wall (Roman, northern England) from the viscous behavior of two

of three blocks tested. This success is somewhat unanticipated because

it implies that S is constant for times of historical length, contrary to

most laboratory observations. Multidomain grains, with their lower S

values, may perhaps succeed where single-domain grains would fail.

More recently, Borradaile has successfully used ad hoc relations

between t

and T

for specific limestones used in the construction of

buildings and monuments in England and Israel to interpret VRM ther-

mal demagnetization data of samples from other structures of unknown

age (see Borradaile, 2003 and references therein). The success of this

approach depends on constructing a calibration (t

, T

) curve using

samples from buildings of known age. It is specific to a certain area

and a particular building stone, and requires substantial labor in estab-

lishing the calibration curve, but is undeniably useful to archeologists

thereafter.

VRM in rocks

Lunar rocks owe their magnetic properties to metallic iron. Lunar soils

and low-grade breccias contain ultrafine (0.02 mm) single-domain

grains which are potently viscous. High-grade breccias, basalts, and

anorthosites have weaker viscous magnetizations originating in multi-

domain iron. For a full discussion, see Dunlop (1973) or Dunlop and

Özdemir (1997, Chapter 17).

Terrestrial submarine basalts are rather weakly viscous. Coarse-

grained massive flows, on the other hand, can be extremely viscous

(Lowrie and Kent, 1978). The VRM is likely due to large homoge-

neous titanomagnetite grains with easily moved walls. VRM of titano-

maghemites is very dependent on the degree of oxidation (see Dunlop

and Özdemir, 1997, Chapter10).

For Tertiary and early Quaternary subaerial basalts, Brunhes epoch

VRM averages about one-quarter of total NRM intensity (Prévot,

1981). Soft VRM is due to homogeneous multidomain titanomagnetite

grains (cf. Figure M141). Relatively hard VRM is carried by single-

domain size magnetite-ilmenite intergrowths formed by oxyexsolution.

Thermal cleaning to 300



C erases all Brunhes epoch VRM, as

Eq. (12) suggests.

Red sediments of all types have relatively strong and hard VRMs.

Creer’s (1957) study remains the classic. Among magnetite-bearing

sedimentary rocks, limestones have been the most thoroughly studied

(e.g., Borradaile, 2003).

Plutonic rocks, especially intermediate and felsic ones, tend to be

quite viscous. The VRM is generally due to multidomain magnetite in

grains 100 mm in size and is easily AF demagnetized (

H <10 mT).

The primary TRM sometimes resides in elongated single-domain mag-

netite grains within silicate host minerals, and is physically as well as

thermoviscously distinct from VRM.

Soils and baked clays, e.g., pottery and bricks, owe their viscous

magnetization to fine single-domain magnetite and maghemite. The

classic study is Le Borgne (1960).

David J. Dunlop

Bibliography

Biquand, D., and Prévot, M., 1971. AF demagnetization of viscous

remanent magnetization in rocks. Zeitschrift für Geophysik, 37:

471–485.

Borradaile, G.J., 2003. Viscous magnetization, archaeology and

Bayesian statistics of small samplesfrom Israel and England. Geophy-

sical Research Letters, 30(10): 1528, doi:10.1029/2003GL016977.

Creer, K.M., 1957. The remanent magnetization of unstable Keuper

marls. Philosophical Transactions of the Royal Society of London,

A250: 130–143.

Dunlop, D.J., 1973. Theory of the magnetic viscosity of lunar and terres-

trial rocks. Reviews of Geophysics and Space Physics, 11:855–901.

Dunlop, D.J., 1983. Viscous magnetization of 0.04–100 mm magne-

tites. Geophysical Journal of the Royal Astronomical Society, 74:

667–687.

Dunlop, D.J., and Özdemir, Ö., 1990. Alternating field stability of

high-temperature viscous remanent magnetization. Physics of the

Earth and Planetary Interiors, 65: 188–196.

Dunlop, D.J., and Özdemir, Ö., 1997. Rock Magnetism: Fundamentals

and Frontiers. Cambridge: Cambridge University Press.

Dunlop, D.J., and Özdemir, Ö., 2000. Effect of grain size and domain

state on thermal demagnetization tails. Geophysical Research Let-

ters, 27: 1311–1314.

Figure M146 Continuous thermal demagnetization of VRMs

produced at 225



C in a synthetic multidomain magnetite sample

with different initial states: crosses, AF demagnetized; solid circles

and triangles, thermally demagnetized and then heated to 225



open circles, zero-field cooled from the Curie point to 225



(after Halgedahl, 1993).

MAGNETIZATION, VISCOUS REMANENT (VRM) 629

Dunlop, D.J., Schmidt, P.W., Özdemir, Ö., and Clark, D.A., 1997.

Paleomagnetism and paleothermometry of the Sydney Basin. 1.

Thermoviscous and chemical overprinting of the Milton Monzo-

nite. Journal of Geophysical Research, 102: 27271–27283.

Dunlop, D.J., Özdemir, Ö., Clark, D.A., and Schmidt, P.W., 2000.

Time-temperature relations for the remagnetization of pyrrhotite

(Fe

) and their use in estimating paleotemperatures. Earth and

Planetary Science Letters, 176: 107–116.

Enkin, R.J., and Dunlop, D.J., 1988. The demagnetization temperature

necessary to remove viscous remanent magnetization. Geophysical

Research Letters, 15: 514–517.

Fox, J.M.W., and Aitken, M.J., 1980. Cooling-rate dependence of

thermoremanent magnetisation. Nature, 283: 462–463.

Halgedahl, S.L., 1993. Experiments to investigate the origin of anom-

alously elevated unblocking temperatures. Journal of Geophysical

Research, 98: 22443–22460.

Heider, F., Halgdahl, S.L., and Dunlop, D.J., 1988. Temperature

dependence of magnetic domains in magnetite crystals. Geophysi-

cal Research Letters, 15: 499–502.

Heller, F., and Markert, H., 1973. The age of viscous remanent magne-

tization of Hadrian’s Wall (northern England). Geophysical Jour-

nal of the Royal Astronomical Society, 31: 395–406.

Jackson, M., and Worm, H.-U., 2001. Anomalous unblocking tem-

peratures, viscosity and frequency-dependent susceptibility in the

chemically-remagnetized Trenton limestone. Physics of the Earth

and Planetary Interiors, 126:27–42.

Le Borgne, E., 1960. Étude expérimentale du traînage magnétique

dans le cas d’un ensemble de grains magnétiques très fins dispersés

dans une substance non magnétique. Annales de Géophysique, 16:

445–494.

Lowrie, W., and Kent, D.V., 1978. Characteristics of VRM in oceanic

basalts. Journal of Geophysics, 44: 297–315.

Middleton, M.F., and Schmidt, P.W., 1982. Paleothermometry of the

Sydney Basin. Journal of Geophysical Research, 87: 5351–5359.

Moskowitz, B.M., 1985. Magnetic viscosity, diffusion after-effect, and

disaccommodation in natural and synthetic samples. Geophysical

Journal of the Royal Astronomical Society, 82: 143–161.

Mullins, C.E., and Tite, M.S., 1973. Magnetic viscosity, quadrature

susceptibility, and frequency dependence of susceptibility in single-

domain assemblies of magnetite and maghemite. Journal of Geophy-

sical Research, 78:804–809.

Néel, L., 1949. Théorie du traînage magnétique des ferromagnétiques

en grain fins avec applications aux terres cuites. Annales de Géo-

physique, 5:99–136.

Néel, L., 1955. Some theoretical aspects of rock magnetism. Advances

in Physics, 4: 191–243.

Perrin, M., 1998. Paleointensity determination, magnetic domain struc-

ture, and selection criteria. Journal of Geophysical Research, 103:

30591–30600.

Prévot, M., 1981. Some aspects of magnetic viscosity in subaerial and

submarine volcanic rocks. Geophysical Journal of the Royal Astro-

nomical Society, 66: 169–192.

Pullaiah, G., Irving, E., Buchan, K.L., and Dunlop, D.J., 1975. Magne-

tization changes caused by burial and uplift. Earth and Planetary

Science Letters, 28: 133–143.

Saito, T., Ishikawa, N., and Kamata, H., 2003. Identification of mag-

netic minerals carrying NRM in pyroclastic-flow deposits. Journal

of Volcanology and Geothermal Research, 126: 127–142.

Shimizu, Y., 1960. Magnetic viscosity of magnetite. Journal of Geo-

magnetism and Geoelectricity, 11: 125–138.

Thellier, E., 1938. Sur l’aimantation des terres cuites et ses applications

géophysiques. Annales de l’Institut de Physique Globe de l’Univer-

sité de Paris, 16: 157–302

Tivey, M., and Johnson, H.P., 1984. The characterization of viscous

remanent magnetization in large and small magnetite particles.

Journal of Geophysical Research, 89: 543–552.

Walton, D., 1980. Time-temperature relations in the magnetization of

assemblies of single-domain grains. Nature, 286: 245–247.

Walton, D., 1983. Viscous magnetization. Nature, 305: 616–619.

Walton, D., and Dunlop, D.J., 1985. The magnetization of a random

assembly of interacting moments. Solid State Communications,

53: 359–362.

Cross-references

Archeomagnetism

Iron Sulfides

Magnetic Domain

Magnetic Susceptibility

Magnetization, Natural Remanent (NRM)

Magnetization, Thermoremanent (TRM)

MAGNETOCONVECTION

Magnetoconvection refers to the thermal driving of flow within an

electrically conducting fluid in the presence of an imposed magnetic

field. In rapidly rotating systems like the Earth’s fluid outer core, mag-

netoconvection offers a key insight into the intricate interaction

between the effects of rotation and magnetic field. The simplest pro-

blem of magnetoconvection is given by a rotating plane horizontal

layer of an electrically conducting Boussinesq fluid across which a

uniform vertical magnetic field is imposed (Chandrasekhar, 1961;

Roberts, 1978; Soward, 1979; Aurnou and Olson, 2001). The mathe-

matical simplicity of the problem provides an essential understanding

of the fundamental magnetohydrodynamic processes taking place in

the Earth’s fluid core. We shall use this example to illustrate these pri-

mary features of general magnetoconvection. For convenience and to

avoid unnecessary complication, we assume that the fluid has constant

viscosity n, thermal diffusivity k, and magnetic diffusivity l. The thick-

ness of the horizontal layer is taken to be d. We further suppose that

magnetoconvection is stationary and that the amplitude of the convec-

tion is sufficiently small so that the nonlinear effects can be safely

ignored. The lower boundary of the layer is heated to maintain a con-

stant negative vertical temperature gradient b. When b is small, mag-

netoconvection cannot occur and the static equilibrium is described by

¼ 0; B ¼ kB

; rT

¼bk; rp

þ kgr ¼ 0 (Eq. 1)

where u

is the fluid velocity, k is the unit upward vector, p

is the

total pressure (kinematic plus magnetic), r is the density of the fluid,

g is the acceleration due to gravity, B is the imposed vertical uniform

magnetic field, and T

is the conduction temperature. When b is suffi-

ciently large, magnetoconvection takes place and modifies the basic

static state. The problem of magnetoconvection is characterized by

the Rayleigh number R, the Taylor number T

, and the Chandrasekhar

number Q, which are defined as

R ¼

abgd

; T

2Od



; Q ¼

mnrl

(Eq. 2)

where m is the magnetic permeability and O is the angular velocity of

the Earth. The Rayleigh number R provides a measure of the vertical

buoyancy force, the Chandrasekhar number Q represents the ratio of

the Lorentz force to the viscous force, and the Taylor number T

the squared ratio of the Coriolis force to the viscous force. The main

characteristics of magnetoconvection can be elucidated in terms of

these three physical parameters.

630 MAGNETOCONVECTION

By assuming that the fluid layer has an infinitely horizontal extent,

solutions of stationary magnetoconvection at onset can be expressed in

the form

uðx; y; zÞ!uðzÞexp½iða

x þ a

yÞ; (Eq. 3)

where u is the velocity of the magnetoconvection, and a

and a

are

the horizontal wave numbers with the total horizontal wave number

a defined as

¼ a

þ a

: (Eq. 4)

When the temperatures of the upper and lower boundaries are held

constant, the flow velocity is stress-free at the boundaries and the

magnetic field satisfies the stress-free-type condition discussed by

Chandrasekhar (1961), the Rayleigh number R at the onset of

magnetoconvection is given by

R ¼

½x

þ Qp



ðx

þ Qp

Þx

þ T

þ Qðx

þ Qp

Þp



;

(Eq. 5)

where w

 a

þ p

. The physically realizable form of magnetocon-

vection is characterized by the smallest value of the Rayleigh number,

which is referred to as the critical Rayleigh number R

. The subtle phy-

sics contained in Eq. (5) can be clearly unfolded by considering a

number of extreme cases.

Magnetoconvection with strong field, weak rotation

When the system is slowly rotating in the absence of an imposed mag-

netic field, Chandrasekhar (1961) showed that the critical Rayleigh

number R

and the corresponding critical wave number of magneto-

convection a

are given by



27p

; a



ﬃﬃﬃ

; for Q ¼ 0 (Eq. 6)

However, both the critical Rayleigh number R

and wave number a

increase dramatically when a strong magnetic field is present

 Qp

; a





1=6

; for Q  1 (Eq. 7)

Comparison between Eqs. (6) and (7) indicates that the role of

the magnetic force is strongly stabilizing: the presence of an intense

magnetic field requires a much larger Rayleigh number to excite

magnetoconvection.

Magnetoconvection with weak field, strong rotation

The Proudman-Taylor theorem states that infinitesimal, nonmagnetic

steady flows in a rotating inviscid fluid are two-dimensional with

respect to the direction of the rotation axis. It follows that the Proud-

man-Taylor constraint must be broken in order that convection can

occur in rapidly rotating systems. In consequence, a large viscous

force in association with small-scale convection cells is usually

required. When the system rotates rapidly and the imposed magnetic

field is weak, we obtain from Eq. (5)



2=3



2=3

; a





1=6

; for T

 1 (Eq. 8)

Comparison of Eqs. (6) and (8) indicates that the role of the Coriolis

force is also strongly stabilizing: the effect of rapid rotation makes

convection difficult.

Magnetoconvection with magnetic and Coriolis forces

in balance

When the rotational effect is predominant (T

 1 and Q  1), mag-

netoconvection is ineffective, invoking large viscous effects in connec-

tion with the short horizontal length of the flow; when the effect of the

magnetic field is dominant (Q  1 and T

 1), magnetoconvection

has similar features. However, when the two inhibiting effects, rotation

and magnetic field, act simultaneously and have a comparable strength

(Q  T

1/2

), magnetoconvection operates in the optimum state: both

the critical Rayleigh number R

and the critical wave number a

reach

an overall minimum. In other words, convection can be most readily

excited when Lorentz and Coriolis forces are of comparable amplitude.

Several examples calculated from Eq. (5) are shown in Figure M147

for T

1/2

¼ 0, 10

,10

. The overall minimum for R

and a

can be

explained by the fact that the effect of the magnetic field relaxes the

Figure M147 The critical Rayleigh number R

(top panel) and

the corresponding wave number a

(lower panel), calculated

using Eq. (5), are shown as functions of the Chandrasekhar

number Q for different values of t, where t ¼ T

1=2

MAGNETOCONVECTION 631

Proudman-Taylor constraint, increases the length scale of the magneto-

convection cell and, hence, makes the system convect more readily

and efficiently. This characteristic of magnetoconvection has led to

an important suggestion that the dynamo of the Earth’s core operates

in the regime T

1/2

 Q where the geodynamo as a thermal engine is

most effective.

Magnetoconvection in spherical geometry

In rotating spherical geometry, magnetoconvection in the presence of

an imposed azimuthal field whose strength is proportional to distance

from the rotation axis has been extensively studied (for example,

Fearn, 1979, 1998; Proctor, 1994). Spherical magnetoconvection exhi-

bits similar features in a plane layer: the critical Rayleigh number R

reaches an overall minimum as the magnetic field strength increases

to Q ¼ O(T

1/2

) at which the Lorentz and Coriolis forces are of com-

parable size. For larger values of Q, the effects of the magnetic field

inhibit convection and thus R

increases with growing Q; for smaller

values of Q, the small scale of the convection cells resulting from

the rotational constraint leads to extremely large R

It should be pointed out, however, that spherical magnetoconvection

in the presence of a more realistic magnetic field that satisfies electri-

cally insulating boundary conditions shows a quite different behavior

(Fearn and Proctor, 1983; Zhang, 1995). It was found that the two-

dimensionality of purely thermal convection survives under the influ-

ence of a strong Lorentz force and that there exist no optimum values

of Q that can give rise to an overall minimum of the critical Rayleigh

number (Zhang, 1995). The value of R

is a monotonically, smoothly

decreasing function of Q. This is because the more realistic magnetic

field can become unstable when Q is sufficiently large (Zhang and

Fearn, 1993).

Keke Zhang and Xinhao Liao

Bibliography

Aurnou, J.M., and Olson, P.L., 2001. Experiments on Rayleigh-

Bénard convection, magnetoconvection and rotating magnetocon-

vection in liquid gallium. Journal of Fluid Mechanics, 430:

283–307.

Chandrasekhar, S., 1961. Hydrodynamic and Hydromagnetic Stability.

Oxford: Clarendon Press.

Fearn, D.R., 1979. Thermal and magnetic instabilities in a rapidly

rotating sphere. Geophysics, Astrophysics, and Fluid Dynamics,

14: 103–126.

Fearn, D.R., 1998. Hydromagnetic flow in planetary cores. Reports on

Progress in Physics, 61: 175–235.

Fearn, D.R., and Proctor, M.R.E., 1983 Hydromagnetic waves in a

differentially rotating sphere. Journal of Fluid Mechanics, 128:

1–20.

Proctor, M.R.E., 1994. Convection and magnetoconvection in a

rapidly rotating sphere. In Proctor, M.R.E., and Gilbert, A.D.

(eds.), Lectures on Stellar and Planetary Dynamos. Cambridge:

Cambridge University Press, pp. 75–115.

Roberts, P.H., 1978. Magneto-convection in a rapidly rotating fluid.

In Roberts, P.H., and Soward, A.M. (eds.), Rotating Fluids in Geo-

physics. London: Academic Press, pp. 421–435.

Soward, A.M., 1979. Thermal and magnetically driven convection in

a rapidly rotating fluid layer. Journal of Fluid Mechanics, 90:

669–684.

Zhang, K., 1995. Spherical shell rotating convection in the presence

of toroidal magnetic field. Proceedings of the Royal Society of Lon-

don Service A, 448: 245–268.

Zhang, K., and Fearn, D., 1993. How strong is the invisible compo-

nent of the magnetic field in the Earth’s core? Geophysical

Research Letters, 20: 2083–2088.

Cross-references

Core Convection

Core Motions

Geodynamo

Magnetohydrodynamic Waves

Proudman-Taylor Theorem

MAGNETOHYDRODYNAMIC WAVES

Introduction

Magnetohydrodynamic waves are propagating disturbances found in

electrically conducting fluids permeated by magnetic fields where

magnetic tension provides a restoring force on fluid parcels moving

across field lines. The role played by magnetohydrodynamic waves,

transporting disturbances in the flow and magnetic field and connect-

ing disparate regions of the fluid, is crucial to our understanding of

hydromagnetic systems. Magnetohydrodynamic waves in the Earth’s

liquid iron outer core have been proposed as the origin of changes of

the Earth’s magnetic field taking place on timescales of decades to

centuries, and are thus of interest to both geomagnetists and paleomag-

netists.

In the Earth’s outer core, in addition to the magnetic forces acting

on the electrically conducting fluid, we must also consider Coriolis

forces resulting from planetary rotation, buoyancy forces due to grav-

ity acting on density gradients and the constraints placed on flow by

spherical shell geometry. Magnetohydrodynamic waves could be

excited by convection-driven instabilities (Braginsky, 1964), topogra-

phically as flow is forced over bumps at the core-mantle boundary

(Hide, 1966), by instabilities of the background magnetic field (Ache-

son, 1972), or even tidally due to deviations of rotating core geometry

from exact sphericity (Kerswell, 1994).

This article focuses on the likely properties of magnetohydrody-

namic waves in the Earth’s outer core and provides a review of

attempts to observe them. After a brief account of the history of inves-

tigations into magnetohydrodynamic waves in the section “Historical

Review,” the physics underpinning their existence will be described

in the section “Force Balance and Waves in Rapidly Rotating Hydro-

magnetic Fluids.” In particular, attention will focus on the emergence

of a new characteristic timescale associated with such waves in rotat-

ing magnetohydrodynamic systems. Dispersion relations for magneto-

hydrodynamic waves when magnetic, buoyancy (Archimedes), and

Coriolis forces are of equal importance (MAC waves) will be derived

and interesting properties are noted in the section “Dispersion Rela-

tions for MC/MAC Waves in the Absence of Diffusion.” The influence

of diffusion, spherical geometry, and nonlinear effects on the waves

will be discussed in the sections “Effects of Diffusion on MC/MAC

Waves,”“Influence of Spherical Geometry on MC/MAC Waves,” and

“Nonlinear Magnetohydrodynamic Waves,” respectively. In the section

“Magnetohydrodynamic Waves in a Stratified Ocean at the Core

Surface,” the suggestion that a stratified layer may exist at the top

of the Earth’s outer core is described and the type of waves that

could be present there will be discussed. Finally, in the section

“Magnetohydrodynamic Waves as a Mechanism for Geomagnetic

Secular Variation,” attempts to identify the presence of magnetohydro-

dynamic waves in the Earth’s outer core through observations of the

Earth’s magnetic field will be reviewed and suggestions made as to

how the wave hypothesis of geomagnetic secular variation could be

tested using a combination of dedicated modeling and rapidly improv-

ing high-resolution observations.

For further details, the interested reader should consult the over-

views by Hide and Stewartson (1972) and Braginsky (1989) or look

in the textbooks by Moffatt (1978) or Davidson (2001). More technical

reviews of the subject include Roberts and Soward (1972), Acheson

632 MAGNETOHYDRODYNAMIC WAVES

and Hide (1973), Eltayeb (1981), Proctor (1994), and Zhang and

Schubert (2000).

Historical review

Study of magnetohydrodynamic waves, especially with a focus on

geophysical applications has a rich history and has captured the atten-

tion of some of the finest applied mathematicians and theoretical geo-

physicists over the past 50 years. Alfvén (1942) initiated the study of

magnetohydrodynamic waves, investigating the simplest possible sce-

nario where a balance of magnetic tension and inertia gives rise to

waves, which became known as Alfvén waves in his honor (see Alfvén

Hannes and Alfvén waves). Lehnert (1954) deduced that rapid rotation

of the fluid system would lead to the splitting of plane Alfvén waves

into two circularly polarized, transverse waves, one with period similar

to inertial waves (a consequence of the intrinsic stability endowed

to fluids by rotation) and a second with a much longer period. The

latter represents a new, fundamental, timescale for rotating hydro-

magnetic systems which we shall refer to as the magnetic-Coriolis (MC)

timescale. Chandrasekhar (1961) studied the effects of buoyancy on

rotating magnetic systems, focusing primarily on axisymmetric motions

invariant about the rotation axis. Braginsky (1964, 1967) realized the

importance of nonaxisymmetric disturbances and showed that if mag-

netic, buoyancy, and Coriolis forces were equally important, fast inertial

modes and slower magnetic modes would again result, but with periods

also dependent on the strength of stratification. He christened these

waves dependent on magnetic, buoyancy (Archimedes), and Coriolis forces

as “MAC waves.”

Hide (1966) was the first to consider the influence of spherical geo-

metry on magnetohydromagnetic waves in a rotating fluid, studying

the effects of the variation of Coriolis force with latitude. He showed

that the resulting MC waves (commonly called MC Rossby waves)

had the correct timescale to account for some parts of the geomagnetic

secular variation, particularly its westward drift (see Westward drift).

Malkus (1967) studied MC waves in a full sphere considering the spe-

cial case when the background field increased in strength with distance

from the rotation axis.

Elteyab (1972), Roberts and Stewartson (1974), Busse (1976),

Roberts and Loper (1979), and Soward (1979) have demonstrated the

importance of including magnetic and thermal diffusion in models of

MAC waves, showing that the most unstable MAC waves in plane layer

and annulus systems often occur on diffusive timescales. Elteyab and

Kumar (1977) and Fearn (1979) carried out the first numerical studies

of magnetohydrodynamic waves to include the effects of both buoyancy

and diffusion in a rotating, spherical geometry. Fearn and Proctor (1983)

went on to consider the effect of more geophysical physically plausible

background magnetic fields and nonzero mean azimuthal flows. Most

recently, Zhang and Gubbins (2002) have discussed the properties of

convection-driven MAC and MC waves in a spherical shell geometry,

studying a variety of background field configurations.

Force balance and waves in rapidly rotating

hydromagnetic fluids

A physical understanding of MC waves can be achieved through con-

sideration of the force balance in a rotating, electrically conducting,

inviscid fluid that involves inertia, magnetic tension resisting flow

across field lines (see Alfvén waves and Magnetohydrodynamics),

and Coriolis forces acting normal to flows and to the axis of rotation.

Coriolis forces are well known for causing circulating eddies in the

atmosphere (e.g., hurricanes) and arise because, in a rotating reference

frame, inertial motions follow curved trajectories rather than straight

lines. It is useful to think about rotation imparting vorticity to a fluid,

in the same way that magnetic fields impart tension perpendicular to

magnetic field lines; vorticity imparts tension perpendicular to vortex

lines (which lie parallel to the rotation axis) leading to a restoring force

when fluid flows across them.

In this system, four possible force balances are conceivable. The

first three require rapid fluid motions while the final is only possible

for slow fluid motions. They are as follows:

1. When magnetic forces are much stronger than Coriolis forces; mag-

netic tension alone balances inertia and disturbances are communi-

cated by Alfvén waves (see Alfvén waves).

2. When Coriolis forces are much stronger than magnetic forces; vor-

tex tension balances inertia and disturbances are communicated by

inertial waves.

3. When magnetic and Coriolis forces are of similar strength; a com-

bination of magnetic field tension and vortex tension balances iner-

tia and disturbances are communicated by inertial magnetic Coriolis

(inertial-MC) waves.

4. When fluid motions are slow so that inertia is unimportant in the

leading order force balance but magnetic and Coriolis forces are

of similar strength; in this scenario, magnetic and vortex tension

are in balance and disturbances are communicated by MC waves.

Balance (4) thus permits the existence of a new class of slow wave in

rotating hydromagnetic systems, which is absent in nonmagnetic and

nonrotating systems. Time dependence in this case arises only through

changes in the magnetic field that, via the Lorentz force, produces

changes in the fluid flow.

An estimate of the MC timescale can be obtained by performing a scale

analysis of the important terms in the equations for conservation of

momentum and magnetic induction. In the momentum equation, Coriolis

and magnetic (Lorentz) forces are in balance, so 2 OU ¼ B

=rL

where O is the angular rotation rate, U is a typical velocity scale,

B is a typical magnetic field strength, L

is a typical length scale

over which changes associated with MC waves occur, r is the den-

sity of the fluid, and is the fluid’s magnetic permeability. We also

know that for a highly conducting fluid, changes in the magnetic

field come primarily from advection, so scale analysis of the induc-

tion equation ignoring diffusion yields B=T

¼ UB=L

, where

is a typical timescale over which changes associated with

MC waves occur. Substituting this expression for U into the force

balance leads to the relation T

¼ 2OL

r=B

. The quantity

¼ B=ðrÞ

1=2

has units of velocity and is the phase speed of Alfvén

waves (see Alfvén waves). Estimates for these quantities in the Earth’score

are V ¼7:3 10

5

1

, r ¼110

kg, ¼4p 10

7

mkg

1

,so

that T

¼10

6

. Neither the magnetic field strength nor the

length scale associated with its variation in the Earth’scoreiswellknown.

Taking B ¼510

4

T as suggested by observations at the core surface

and L

¼3:510

m, the core radius, yields T

1:510

Equally plausibly, if we are consider a wave with azimuthal wave

number 8, and assume that the field inside the outer core is 10 times

the observed core surface field strength we find T

 235 years. The

coincidence between the latter MC wave timescale and that of geomag-

netic secular variation motivates attempts to link the two phenomena.

In the Earth’s core, it is likely that buoyancy forces (either thermal

or compositional) could also be important in the primary force balance

(see Core convection). In the remainder of this article we shall there-

fore generalize our discussion to include buoyancy, which modifies

the MC timescale to a MAC timescale because Archimedes forces

are now present. In the next section we present an outline of the deri-

vation of the dispersion relation for MAC waves.

Dispersion relations for MC/MAC waves in the absence

of diffusion

To focus the discussion, while keeping mathematics to a minimum, we

shall consider a rather basic model of a rapidly rotating, electrically

conducting, incompressible fluid in an infinite three-dimensional

domain, where there are no dissipative processes (viscous, magnetic,

or thermal diffusion) operating. Buoyancy forces are included via the

MAGNETOHYDRODYNAMIC WAVES 633

Boussinesq model, with the degree of stratification depending on the

magnitude of the background temperature gradient.

We shall work in Cartesian coordinates (

z) with the axis of rota-

tion along

z, a uniform background field B

¼ðB

x þ B

y þ B

zÞ

and a uniform background temperature gradient of bbz.Ifa is the

thermal expansivity of the fluid, then density is determined by the rela-

tion r ¼ r

ð1 þ aYÞ where Y is the perturbation from the background

temperature field, so that in a gravity field of g

z there will be a buoy-

ancy force of magnitude gaY in the

z direction.

We shall consider small perturbations ðu; b; YÞ about a state of

no motion (so the background velocity field is zero) and consider

only slow motions so that inertial terms can be neglected and atten-

tion can focus on the MC force balance. The linearized equations

governing the evolution of small perturbations are then the momentum

equation

2V u

|ﬄﬄﬄ{zﬄﬄﬄ}

Coriolis

acceleration

due to rotation

¼

|ﬄﬄﬄ{zﬄﬄﬄ}

acceleration

due to pressure

gradient

rðÞb

|ﬄﬄﬄﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄﬄﬄﬄ}

acceleration

due to

field tension

þ gaY

|ﬄﬄ{zﬄﬄ}

buoyant

acceleration

;

(Eq. 1)

the induction equation

|{z}

Change in the

magnetic field

¼ðB

rÞu

|ﬄﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄﬄ}

Stretching of magnetic

field by fluid motion

; (Eq. 2)

and temperature equation

|{z}

Change in the

temperature field

¼ bð

z  uÞ

|ﬄﬄﬄ{zﬄﬄﬄ}

advection of temperature

field by fluid motion

: (Eq. 3)

Taking ]=]tðrÞ the momentum equation (1) to eliminate pressure

gives

2ðV rÞ

ðB

rÞ

]

ðr  bÞþga

]

ðr  Y

zÞ; (Eq. 4)

while taking the curl (r ) of the induction equation (2) we find,

]

ðr  bÞ¼ðB

 rÞðr  uÞ: (Eq. 5)

Substituting from Eq. (5) into Eq. (4) for ]=]tðr  bÞ gives a vorticity

equation quantifying the MAC balance with terms arising from Corio-

lis forces on the left-hand side and terms arising from the magnetic and

buoyancy forces on the right-hand side

2ðV rÞ

ðB

rÞ

ðr  uÞþga

]

ðr  Y

zÞ: (Eq. 6)

Operating on Eq. (6) with ððB

rÞ

rÞ=r, we can then eliminate

ððB

rÞ

ruÞ=r from the term on the left-hand side by using

Eq. (6) once again. By utilizing the well-known relation for incom-

pressible fluids that rru ¼r

u, and then taking the dot

product with

z while noting that

z ðrY

zÞ¼0 and

z ðrrY

zÞ¼ð]

=]x

þ ]

=]y

ÞY ¼r

Y leaves

4ðV rÞ

]

¼

ðB

rÞ

 ga

ðB

rÞ

Finally, we make use of the temperature Eq. (3) to eliminate ]Y=]t

and obtain a sixth-order equation in u

, which we shall refer to as

the diffusionless MAC wave equation

4ðV rÞ

]

ðB

rÞ

gab

ðB

rÞ

¼ 0:

Properties of diffusionless MAC waves can now be deduced

by substitution of plane traveling wave solutions of the form

¼ Ref

iðkrotÞ

g, where k is the wavevector and o is the angular

frequency

4ðV  kÞ



ðB

 kÞ



ðB

 kÞ

gabðk

þ k

Þ¼0:

(Eq. 7)

This expression can be written more concisely by observing that terms

in it correspond to characteristic natural frequencies for magnetic-iner-

tial (Alfvén) waves, gravity waves, and inertial waves in rotating

fluids, respectively

ðB

 kÞ

; o

gabðk

þ k

; o

4ðV  kÞ

;

(Eq. 8)

so Eq. (7) simplifies to

 o

¼ 0: (Eq. 9)

Solving for o gives the necessary condition (or dispersion relation)

that must be satisfied by the angular frequency and wavevectors of

plane MAC waves,

o ¼

1þ



1=2

¼

kðB

kÞ

2rðV kÞ

1þ

gabrðk

þk

ðB

kÞ

1=2

(Eq. 10)

Note that this is singular if B

 k ¼ 0orifV  k ¼ 0, so diffusionless

MAC waves cannot propagate normal to magnetic field lines or

the rotation axis. Their frequency depends strongly on their wavelength

(i.e., they are highly dispersive) and on their direction (i.e., they are ani-

sotropic). In the special case when the background magnetic field and

the direction of the rotation axis are parallel to the direction of wave pro-

pagation, and when buoyancy forces are absent ða ¼ 0Þ, the dispersion

relation simplifies to o ¼ B

=2Or or T

¼ 2OrL

as was

deduced from scaling arguments in the previous section. The phase

speed of the waves is then c ¼o=k ¼B

k=2Or and it is seen that waves

with shorter wavelengths travel faster.

Effects of diffusion on MC/MAC waves

So far we have neglected the influence of any source of dissipation

(viscous, magnetic, or thermal diffusion) on the system in order to sim-

plify both the mathematical analysis and the physical picture. It is now

necessary to consider their effects. Naively, we might expect the pre-

sence of dissipation should merely damp disturbances and irreversibly

transform energy to an unusable form. Although such processes

634 MAGNETOHYDRODYNAMIC WAVES

undoubtedly occur, they are not the only effects of the presence of dif-

fusion. Perhaps more importantly, diffusion adds extra degrees of free-

dom to the system and facilitates the destabilization of waves that are

stable in the absence of diffusion (see Roberts and Loper, 1979). This

rather counterintuitive effect means that instability of MAC/MC waves

can occur for smaller unstable density or magnetic field gradients than

if no diffusion were present. In fact, such diffusive instability turns out

to be possible, even in the presence of a stable density gradient.

The diffusive instability mechanism works most effectively when

the oscillation frequency matches the rate of diffusion, so the timescale

of the most unstable MC/MAC waves will be that of the diffusion pro-

cess that is facilitating the instability. Diffusion thus introduces new

preferred timescales into the MC/MAC wave problem.

To include diffusion in the mathematical description of MAC

waves, we must replace the operator ]=]t by ð]=]t  nr

Þ in the

momentum equation, by ð]=]t  r

Þ in the induction equation and

by ð]=]t  kr

Þ in the heat equation. Retaining the acceleration term

from the momentum equation and including the Laplacian (diffusion)

terms before the substitution of plane wave solutions results in a more

complicated dispersion relation for diffusive MAC waves

ðo þ ik

ðo þ ink

Þðo þ ik

Þo





ðo þ ikk

þ o

ðo þ ik

Þðo þ ink

Þðo þ ik

Þo



¼ 0:

(Eq. 11)

Restricting ourselves to the conditions present in the Earth’s outer

core, where we expect ohmic diffusion to dominate viscous and ther-

mal diffusion (  n; k) and where we can again neglect inertial

accelerations when considering slow oscillations, this expression

simplifies to

ðo þ ik

 o



o  o

ðo þ ik

Þ¼0: (Eq. 12)

The link to diffusionless MC waves becomes apparent if buoyancy

forces are negligible ðo

¼ 0Þ when Eq. (12) reduces to,

o ¼

 ik

: (Eq. 13)

Here the classical damping role of magnetic diffusion is obvious, caus-

ing MC waves with shorter wavelengths to decay in amplitude more

quickly than MC waves with longer wavelengths. More detail on dif-

fusive MC waves and their consequences for on geodynamo simula-

tions can be found in Walker et al. (1998).

Influence of spherical geometry on MC/MAC waves

The Earth’s outer core is not an infinite plane layer, but a thick sphe-

rical shell with an inner radius approximately one-third of its outer

radius. How does spherical shell geometry influence propagation prop-

erties, stability, and the planform of magnetohydrodynamic waves? It

appears that when the magnetic field is strong enough, and the Lorentz

force dominates the force balance in the momentum equation, then the

spherical boundaries play a secondary role. On the other hand, when

the magnetic field is weak, the influence of the Coriolis force and its

latitudinal variations caused by the spherical geometry are crucial.

In the absence of any certain knowledge of the strength of the mag-

netic field in the Earth’s core it is unclear if spherical shell geometry

has a controlling influence on magnetohydrodynamic waves there, so

the safest course is to use spherical geometry and study a variety of

magnetic field strengths.

Hide (1966) was the first to appreciate the importance of the latitu-

dinal dependence of the Coriolis force for waves in the Earth’s core.

He developed a simple analytical model of MC waves retaining only

the linear variation of Coriolis force with latitude (this is known to

meteorologists and oceanographers as a b plane model and is the

necessary ingredient for the restoring force responsible for Rossby

waves). We shall refer to Hide’s waves as magnetic-Coriolis (MC)

Rossby waves. He showed they would propagate westward in a thick

spherical shell and could have a timescale similar to that of geomag-

netic secular variation.

Eltayeb and Kumar (1977) and Fearn (1979) included both thermal

buoyancy and diffusion and worked in spherical geometry. They were

confronted by a rather complex scene, with several different mechan-

isms giving rise to different types of magnetohydrodynamic waves,

any of which could potentially be important in the Earth’s core. They

identified four distinct regimes where different waves were favored.

Only a brief overview of the four possible regimes is presented here.

Type I: Magnetically modi fied, buoyancy-driven

Rossby waves

When the magnetic field is very weak, wave motion is essentially that

produced by convection in a rapidly rotating sphere (i.e., thermal

Rossby waves or Busse rolls—see Core convection). The flow con-

sists of columnar rolls parallel to the rotation axis, arranged on a

cylindrical shell that intersects the outer boundary at midlatitudes. At

the onset of convection and in the absence of any mean azimuthal flow

these waves drift eastward on a thermal diffusion timescale. The plan-

form of the waves is columnar because the Coriolis force promotes

invariance along the rotation axis (see Proudmann-Taylor theorem).

The magnetic field acts only as a small perturbation and actually stabi-

lizes the system, increasing the critical Rayleigh number compared to

the nonmagnetic systems. Instability is driven by the component of

buoyancy perpendicular to the rotation axis and is balanced primarily

by the Coriolis force (varying with latitude due to the spherical geo-

metry) and viscous diffusion.

Type II: Buoyancy-driven magneto-Rossby waves

With stronger magnetic fields, buoyancy is balanced by the magnetic

(Lorentz) force as well as the Coriolis force. The planform of Type II

waves is similar to those of Type I waves and they too propagate on

the thermal diffusion timescale. Both westward and eastward pro-

pagation of these waves is possible, depending on the relative magni-

tudes of magnetic and thermal diffusion. It should be noted that the

magnetic field now plays a destabilizing roll, catalyzing the onset of

convection. The dominant role of the uniform imposed magnetic field

causes an increase in the length scale so that the number of waves

fitting around a cylindrical shell decreases, while the latitude of the rolls

moves toward where the magnetic field is strongest. Figure M148

shows the form of the radial magnetic field disturbance produced by a

magneto-Rossby wave in spherical geometry when the imposed mag-

netic field increases linearly with distance from the rotation axis (the

force-free field of Malkus, 1967). This figure is the result of an eigenva-

lue calculation (using the code of Jones et al., 2003) used to determine

the most unstable wave in a regime when magnetic and Coriolis forces

are approximately of equal magnitude.

Type III: Buoyancy-driven MAC waves

When magnetic forces are much stronger than the Coriolis forces,

boundary curvature associated with spherical geometry plays a less

important role and the most unstable wave is of diffusive MAC-type,

again propagating on the thermal diffusion timescale. The planform of

the waves is no longer that of columnar rolls because the strong mag-

netic fields permit departures from z independence. Both westward-

and eastward-propagating waves are possible in this regime.

MAGNETOHYDRODYNAMIC WAVES 635