Gubbins D., Herrero-Bervera E. Encyclopedia of Geomagnetism and Paleomagnetism

Подождите немного. Документ загружается.

¼ n=; (Eq. 72)

is very small ð10

6

Þ. Assuming that the dissipation length scale for

the viscous energy dissipation Q

is not much smaller than that for

the magnetic energy dissipation Q

, it follows that Q

 Q

(except

possibly in boundary layers). The total ohmic dissipation from the

macroscales has been estimated to lie between 0.1 and 2 TW

ð1TW¼ 10

WÞ with the microscales possibly contributing just as

much (see Section on Some effects of turbulence). Although a definitive

figure is so far unobtainable, the fact that the Earth has possessed a mag-

netic field for most, and perhaps all, of its existence proves that the

necessary power requirements have been met throughout that time,

though the source of that power is not completely certain (see Geody-

namo, energy sources). This article will focus mainly on core convec-

tion, but only in a simplified way. Even though it is often argued that

compositional buoyancy is as (or even more) important as thermal buoy-

ancy in driving core motions, only the latter will be included here, as this

will suffice to illustrate the salient points. For a geophysically more faith-

ful treatment, see Braginsky and Roberts (1995, 2003) and Convection,

chemical and Core convection (q.v.). For MHD models of the geody-

namo, see Geodynamo and Geodynamo, numerical simulations (q.v.).

Basic equations

The aim in much of the remainder of this article is to explore the roles

of the Coriolis, Lorentz, and buoyancy forces. An attempt will be

made to raise the level of complexity gradually and to start from a model

that includes these forces as simply as possible by using the Boussinesq

model (see Anelastic and Boussinesq approximations). Then

H  V ¼ 0; (Eq. 73)

]

V þ V  HV þ 2V  V ¼HP  aT g þ J  B=r þ nr

(Eq. 74)

In this approximation, the density r of the fluid is uniform, so that

mass conservation reduces to the condition (73) of incompressibility.

Momentum conservation (74) is expressed in the reference frame that

corotates with the mantle, at a constant angular velocity V. The resulting

Coriolis acceleration, 2VV, appears on the left-hand side of Eq. (74).

The centrifugal acceleration, V ðV  xÞ, has been combined with the

kinetic pressure, P, to form the reduced pressure, P ¼P=r 

ðV xÞ

The last two terms in Eq. (74) represent the Lorentz and viscous forces

per unit mass. The buoyancy force per unit mass is aT g, where T is

the temperature, a is the thermal expansion coefficient, and g is the

gravitational acceleration, assumed constant in time.

The temperature is governed by an energy equation of the form

T ¼ kr

T þ Q=rC

; (Eq. 75)

where k is the thermal diffusivity and Q comprises the various sources

of heat: Q ¼ Q

þ Q

, where Q

arises from internal sources,

if any, such as dissolved radioactivity; C

is the specific heat at con-

stant pressure. We shall initially consider nonmagnetic systems, but,

when later we generalize to MHD situations, Eqs. (73)– (75) must be

solved in conjunction with Eq. (3) and the induction equation (45).

The boundary conditions for B developed in Section Electrodynamics

must be supplemented by boundary conditions on V and T,suchas

V ¼ 0; on the CMB; (Eq. 76)

T ¼ T

CMB

; on the CMB; (Eq. 77)

where T

CMB

is constant. Equation (76) expresses the no-slip condition

that, at their common interface, the fluid moves with the solid, which

has zero velocity in the chosen reference frame. The SIC contains only

about 5% of the total mass of the core, and its low inertia makes its

rotation rate susceptible to the torques (mainly gravitational and mag-

netic) to which it is subjected (see Eq. (43)). These feature in an equa-

tion of motion for its angular velocity V

SIC

(see Inner core rotational

dynamics). For simplicity, we shall assume that

V ¼ 0; on the ICB; (Eq. 78)

T ¼ T

ICB

; on the ICB; (Eq. 79)

where T

ICB

is constant. When viscous forces are ignored, the differen-

tial order of Eq. (74) is reduced, and it is possible to satisfy only one

condition on V at the boundaries; the first of Eqs. (76) and (78) are

then replaced by

nV ¼ 0; on the CMB and ICB; for n ¼ 0: (Eq. 80)

The relative importance of the various terms of Eqs. (73)–(75) is quan-

tified by several dimensionless groupings, of which the (kinetic) Reynolds

number R

¼VL=n has already been defined. It quantifies the relative

sizes of the inertial and viscous forces. Among the dimensionless

parameters describing convection, special mention should be made of

the Rayleigh number, Ra and the usual (thermal) Prandtl number, P

Ra ¼ gabL

=nk; (Eq. 81)

¼ n=k; (Eq. 82)

where b is, in the Boussinesq approximation, a typical measure of the

temperature gradient, e.g., the difference DT between the temperatures

of the ICB and CMB divided by the depth of the fluid core. (In a layer

as thick as the FOC, however, the compressibility of the fluid is signif-

icant. Convection is better described by the anelastic approximation

and a better choice of b is then the difference between the actual tem-

perature gradient and the adiabatic temperature gradient [see Core,

adiabatic gradient; Anelastic and Boussinesq approximations].) The

Rayleigh number is a measure of how effective the buoyancy force

is in overcoming the diffusive processes that oppose convection.

A popular way to gain insight into convective processes, popular

because the theory is relatively tractable, is to study the onset of con-

vection. A motionless conductive state is defined in which heat is car-

ried across the system by thermal conduction; the linear stability of

this state is then analyzed. It is found that when the control parameter,

Ra, reaches some critical or marginal value, Ra

, the conduction solu-

tion becomes convectively unstable. The eigenfunction corresponding

to Ra

gives the structure of the marginal state of motion. In the

absence of Coriolis and Lorentz forces, Ra

is typically of order 10

and the marginal mode is a pattern of overturning convection cells,

having about the same horizontal scale as the depth L of the convect-

ing layer.

Although studies of this type provide some insight into convective

flows, they clearly have limited value. They predict that, when

Ra > Ra

, the convective motions increase without limit, though in

reality feedback from nonlinearities, such as the inertial term V  HV

in Eq. (74), prevents this. The enhanced amplitudes and modified

structure of the convective motions as Ra is increased from Ra

are

topics that are beyond the competence of linear theory and are also

beyond the scope of this article. Here we shall use the results of linear

stability analyzes to obtain clues about how Coriolis and Lorentz

forces affect thermal convection.

Classical theory of rotating fluids

In this section we shall suppose that B  0; initially, buoyancy is also

excluded ðg  0Þ. We give a rudimentary account of relevant concepts

646 MAGNETOHYDRODYNAMICS

in the theory of rotating fluids. For a more complete treatment, see the

classic text of Greenspan (1968).

Two dimensionless numbers quantify the importance of viscosity

and inertia relative to the Coriolis force, the Ekman number, E, and

the Rossby number, Ro:

E ¼ n=OL

; (Eq. 83)

Ro ¼V=OL: (Eq. 84)

The Ekman number may be called a structural parameter, since,

like P

and P

, its value is determined by the rotation and physical

properties of the Earth, none of which relate to MHD processes in

the core. In contrast, the Ro may be called a response parameter since

its value, like R

and R

, depends on the response of the system to the

physical state in which it finds itself. The molecular viscosity, n

,is

uncertain but is commonly estimated to be about 10

6

1

. Using

this for n in Eq. (83) and taking L¼2  10

m as before, we obtain

E  10

15

. Such a small value suggests that large-scale momentum

is transported more effectively by small turbulent eddies than by molecu-

lar processes, and that E should be estimated using a larger, turbulent

viscosity, n

. A popular paradigm (see, for example, Braginsky and

Meytlis, 1990) assumes that n

 , but even then E does not exceed

9

. Taking, as before, V¼2  10

4

1

, we have Ro  10

5

From the estimates just made, we see that the FOC is a rapidly

rotating fluid, defined as one for which

E  1; (Eq. 85)

Ro  1: (Eq. 86)

The ratio Ro=E ¼VL=n is the (kinetic) Reynolds number R

and is

large. For the geodynamo to exist, R

¼VL= must be of order 10

and, since P

 1, Eq. (85) follows from Eq. (86). The smallness of

Ro means that we may discard one of the inertial terms, V  HV,from

Eq. (74). Looking ahead to the Section on the Classical and Coriolis

MHD, we shall recognize that the nonlinear feedback equilibrating the

geodynamo is the Lorentz force rather than the inertial force.

The remaining inertial term, ]

V, in Eq. (74) is responsible for iner-

tial waves. These are most easily studied by abbreviating Eq. (74) to

]

V þ 2VV ¼HP; (Eq. 87)

and by solving this equation and Eq. (73) subject to Eq. (80). The waves

are dispersive and are obtained by assuming that V is proportional to

expðiotÞ. The spectrum of possible o is discrete, with infinitely many

possible eigenvalues o, all in the range joj2O (see Greenspan,

1968). The closer joj is to zero, the denser the packing of eigenvalues

and the more two-dimensional the eigenfunctions are with respect to

V, which we shall take to be in the z-direction. The extreme case,

o ¼ 0, gives a single, infinitely degenerate eigenfunction called the

geostrophic mode. For this mode, ]

V ¼ 0 and Eqs. (73) and (87) give

2V  HV ¼ 0: (Eq. 88)

Stated in words (see Proudman-Taylor theorem):

The slow steady inviscid motion of a rotating inviscid fluid is

two-dimensional with respect to the rotation axis.

Taking V ¼ O1

, Eq. (88) gives

V ¼ Vðx; yÞ: (Eq. 89)

(Here and elsewhere 1

is the unit vector in the direction of increasing

coordinate q.) Since the CMB and ICB have been assumed to be

spherical (though the following result is equally valid for an axisym-

metric boundary), Eqs. (80) and (89) imply that

V ¼

ðsÞ1

; (Eq. 90)

where ðs; f; zÞ are cylindrical coordinates. The function

ðsÞ is arbi-

trary; this is the infinite degeneracy referred to above. The geostrophic

flow is axisymmetric, zonal, and constant on geostrophic cylinders,

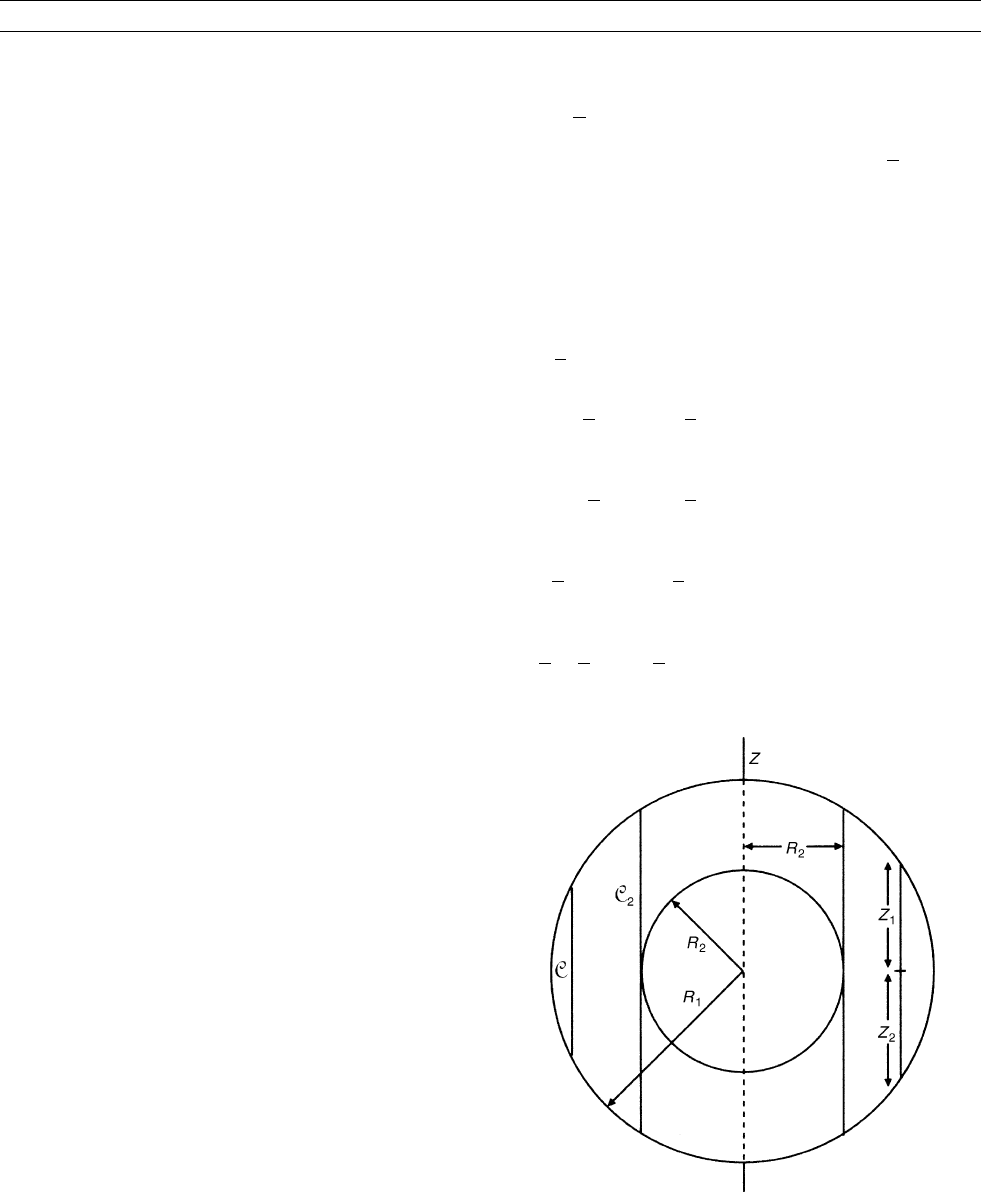
CðsÞ. These are cylinders of constant radius s. Figure M151 shows a

typical geostrophic cylinder and also a particularly significant one,

¼CðR

Þ, which touches the SIC on its equator and is therefore

called the tangent cylinder, abbreviated here to “TC” (see Inner core

tangent cylinder).

For further insight into the geostrophic mode, consider the effect of

a buoyancy force produced by an axisymmetric temperature distri-

bution

T that creates a density stratification frozen into the fluid

ðk ¼ 0Þ. Then Eq. (74) gives

2V 

V ¼HP  aTg: (Eq. 91)

Since H  g ¼ 0, this implies, instead of Eq. (88), that

2V r

V ¼ag  HT : (Eq. 92)

Since gð¼ g1

Þ is radial, this reduces to

]

¼ðga=2OrÞ]

T; (Eq. 93)

which when integrated gives

V ¼½V

ðs; zÞþV

ðsÞ1

: (Eq. 94)

Figure M151 A typical geostrophic cylinder C and a particularly

significant geostrophic cylinder C

called the “tangent cylinder”

that touches the inner core r ¼ R

at its equator. The cylinder of

radius s meets the surface of the outer core, r ¼ R

, on the latitude

circles z ¼ z



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðR

 s

and z ¼ z



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðR

 s

.Ifs < R

there is a northern geostrophic cylinder meeting the inner core

at z ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðR

 s

and a southern geostrophic cylinder meeting

it at z ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðR

 s

MAGNETOHYDRODYNAMICS 647

The flow V

is called the “thermal wind” (see Thermal wind). Its

magnitude is OðgaDT =OÞ and, if this is comparable with our assumed

characteristic velocity V¼2  10

4

1

, the pole-equator tempera-

ture difference DT is, for a  10

5

1

, of the order 10

4

K. This

may be regarded as typical of the temperature differences between ris-

ing and falling fluid throughout the core though, more precisely, when

the compressibility of the core is properly allowed for, it is typical of

the excess or deficit of the temperature relative to the adiabat. The state

(94) may be subject to asymmetric baroclinic instabilities. These are

studied by, for example, Gill (1982).

There is clearly some arbitrariness in Eq. (94), since all or any part

can be absorbed into V

. A convenient way of removing this

arbitrariness is to introduce a geostrophic average. The geostrophic

average of a scalar field Qðx; tÞ is denoted by angle brackets and is

defined for s > R

by:

hQiðs; t Þ¼

AðsÞ

CðsÞ

Qðx; tÞdS ¼

z

Qðs; z; tÞdz: (Eq. 95)

Here  z

ðsÞ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðR

 s

gives the z -coordinates of the latitude

circles where the geostrophic cylinder CðsÞ meets the CMB (see

Figure M151); A ¼ 4psz

ðsÞ is the area of the cylinder and

dS ¼ sdfdz. The ageostrophic part of Qðx; tÞ is what is left over after

the geostrophic part has been subtracted:

Qðx; tÞ¼Qðx; tÞhQiðs; tÞ.

The geostrophic part of a vector field Qðx; tÞ is defined by

hQiðs; tÞ¼hQ

iðs; tÞ1

: (Eq. 96)

It is particularly significant because all the angular momentum about

Oz contained between the shells CðsÞ and Cðs þ dsÞ is accounted for

by V

ðsÞ. The separation (94) is made unique by defining V

¼hVi.

The definitions of hQi and hQi just given apply only when s > R

Inside the TC, there is a geostrophic average for the fluid to the north

of the inner core and another for the fluid to the south.

The thermal wind is illustrative of a more general situation: the

response of a rotating fluid to forcing. We consider

]

V þ 2V V ¼HP þ F; (Eq. 97)

where Fðx; tÞ is assigned and the response V is sought. There are inter-

esting cases in which the forcing has a high frequency. For example, in

the rotating frame, the precessionally driven flow considered earlier

has the same timescale as the inertial waves. Also, diurnal frequencies

may arise from core turbulence. But, on the timescale T of large scale

convection, the modified Rossby number, 1=OT , is small. The

response to F is then a combination of free inertial waves (the solution

to the homogeneous problem (87) defined by Eq. (97)) and a particular

solution that varies slowly, on the same timescale as F. This is the part

of V of greatest interest; the free inertial waves are of lesser signifi-

cance and can be filtered out by discarding the ]

V term in Eq. (97),

so dispensing with the inertial force in its entirety.

Although discarding ]

V is tempting, some caution should be exer-

cised. The geostrophic average of Eq. (97) is

]

þ 2OhV

i¼hF

i: (Eq. 98)

The second term is proportional to the mass flux out of C, and is by

Eqs. (73) and (80):

i

AðsÞ

VdS ¼ 0; (Eq. 99)

so that Eq. (98) becomes

]

¼hF

i: (Eq. 100)

If its left-hand side is omitted, there is no solution to Eq. (100)

unless hF

i¼0. When F is the buoyancy force  aTg alone,

i¼0 because g has no f-component. If F contains the Lorentz

force, however, it is not necessarily true that hF

i¼0, a point to which

we return in the Section on Classical and Coriolis MHD. Meanwhile we

see that one way of evading the difficulty that arises when hF

i 6¼ 0,

while at the same time removing the free inertial waves, is to retain only

the geostrophic part of the inertial force, replacing Eq. (74) by

]

þ 2V  V ¼HP  aT g þ J  B=r þ nr

(Eq. 101)

This is often employed in preference to Eq. (74).

We have so far ignored the effects of viscosity. The smallness (85)

of E encourages an asymptotic approach to determining core flow.

Conceptually, the core is divided into boundary layers, in which viscos-

ity is significant, and the remaining mainstream in which viscosity does

not act at leading order (see Eq. (97)). The most important boundary

layers in rotating fluids are the Ekman layers, the thicknesses of which

are of order d

¼ðn=OÞ

1=2

¼ E

1=2

L0:1 m (see Greenspan, 1968

and Core, boundary layers). The main task of the Ekman layers is to

reconcile mainstream flows with the no-slip conditions (76) and (78).

For example, the mainstream

V obtained from Eq. (97) will not in gen-

eral obey Eq. (76) at the latitude circle ðs; z

Þ, and an Ekman layer forms

that smoothly joins

Vðs; z

Þ to the angular velocity of the CMB (which

is zero by choice of reference frame). Associated with the Ekman layer

is a significant process called Ekman pumping. Although the solution of

Eq. (97) had to satisfy Eq. (80) to leading order, mass conservation in

the Ekman layer requires that, at the next order, a meridional mainstream

flow

ðs; zÞ exists of order E

1=2

Vðs; z

Þ.

This provides an alternative way of overcoming the difficulty

encountered when hF

i 6¼ 0. The outward mass flux hV

i from CðsÞ,

represented by the second term in Eq. (98), can be balanced by an

inward radial flux from the Ekman layers on the northern and southern

radial caps, NðsÞ and SðsÞ, that form the ends of CðsÞ; see Figure

M152 where, for simplicity, complications from the rotation of the

Figure M152 A typical geostrophic cylinder CðsÞ of radius s and

the two spherical caps, NðsÞ and SðsÞ, at its ends. The flux of fluid

out of C through the curved surface of radius s is equal to the

pumping from the Ekman layers on the spherical caps (see text).

648 MAGNETOHYDRODYNAMICS

SIC have been evaded by ignoring its existence. Pumping through the

caps vitiates Eq. (99) and leads to a modification of Eq. (100) in which

a frictional term of order E

1=2

is added to the left-hand side. This

determines the spin-up timescale, t

spin up

, on which changes in the angu-

lar velocity of the mantle are transmitted to the fluid core. By comparing

]

with E

1=2

, we see that t

spin up

 E

1=2

1

 E

1=2

, or about

y. Here t

is the viscous decay time:

¼L

=n: (Eq. 102)

For L¼2  10

m and n

¼ 10

6

1

, this is over 10

y; for

  it is Oðt



Þ.

The effects of viscosity are also felt in complicated shear layers that

surround the TC whenever the SIC does not move with the mantle. For

a discussion of these “Stewartson layers,” see Core, boundary layers.

Viscosity also plays a crucial role in thermal convection. We shall

consider only the case (85) of small E; for simplicity, we suppose that

> 1. We ignore the SIC and suppose that heat sources are distribu-

ted uniformly throughout the core. If these sources are weak, they cre-

ate only a spherically symmetric temperature distribution

ðrÞ that

carries heat out of the core by thermal conduction. Although the asso-

ciated density distribution is top-heavy, the diffusion of heat and

momentum prevents convective instability; but, if the heat sources

are gradually increased, weak convection occurs as soon as Ra exceeds

a critical value, Ra

. For Ra ¼ Ra

, the flow is asymmetric in structure,

not axisymmetric. It takes the form of a “cartridge belt” of two-

dimensional cells, often called Taylor cells, regularly spaced round

the axis of rotation and drifting in longitude about that axis (Roberts,

1968; Busse, 1970; Jones et al., 2000). Adjacent cells spin around

their axes in opposite directions in a sequence of cyclonic and anticy-

clonic vortices, with vorticity respectively parallel and antiparallel to

V. (See Convection, nonmagnetic rotating.) Although, when Ra

exceeds Ra

, nonlinear interactions create other flow components

(including an easily excited geostrophic motion), the cartridge belt

structure is maintained, provided Ra is not too large.

The name Taylor cell is a useful reminder of the Proudman-Taylor

theorem, which the flow is trying to obey by being as two-dimensional

as possible, consistent with allowing convection to occur at all. We

have already seen that, if n ¼ 0, small amplitude motion must be geos-

trophic, since the thermal forcing T

(r) is independent of latitude. But

geostrophic motions have no radial components to carry heat outward.

Convection can occur only if the buoyancy force is large enough to

break the rotational constraint of the theorem. Thus, although Ra

would be O(1) if E were O(1), the critical Rayleigh number is large

when E  1; in fact Ra

¼ OðE

4=3

Þ10

, and the number of cells

in the cartridge belt is then of order E

1=3

 10

, i.e., the scale L

the motions perpendicular to V is OðE

1=3

LÞ  30 m. Convective heat

transport is mainly in the s-direction, i.e., away from the rotation axis

(Busse, 1970). The instability criterion Ra

¼ OðE

4=3

Þ may also be

written as N

¼ðnk =L

1=2

2=3

, where N ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðgabÞ

is the buoy-

ancy frequency that, if imaginary, would usually be called the

Brunt-Väisälä frequency (Gill, 1982). It is worth pointing out that, in

the absence of diffusive effects, the density stratification would

be unstable when N

¼ OðOÞ. This value of N

is greater than

ðnk=L

1=2

2=3

by a large factor, of order E

1=3

. In other words,

the effects of diffusion are destabilizing. There is also a basic

difference between the convective instability that onsets when

Ra ¼ OðE

4=3

Þ and the Rayleigh-Taylor instability of the diffusionless

system. The latter releases gravitational energy in a single spasm

that transforms a top-heavy mass distribution into a bottom-heavy

configuration. The heat conduction necessary to renew constantly the

top-heavy distribution is (by assumption) absent, and therefore the

continuously overturning motions characteristic of thermal convection

do not occur. We return to this topic in the Section on CMHD for

imperfect fluids.

Classical and Coriolis MHD

Classical MHD

In this section we shall suppose that V  0 and initially also exclude

buoyancy ðg  0Þ. We give a rudimentary account of relevant concepts

in the MHD in nonrotating systems. For a more complete treatment,

see Davidson (2001).

Much of classical MHD theory was originally developed to explain

laboratory flows of liquid metals, and two dimensionless numbers

were introduced to quantify the importance of the Lorentz force rela-

tive to the viscous and inertial forces, the Hartmann number, Ha,

and the interaction parameter, N. These can be written in several

equivalent ways:

Ha ¼BL



1=2

ðm

rnÞ

ðnÞ



1=2

ﬃﬃﬃﬃﬃﬃ

;

(Eq. 103)

N ¼

rV

V

: (Eq. 104)

The current J created by motions V in a field B is JsVB so that

the Lorentz force per unit volume is approximately sB

V. This is

greater than the inertial acceleration rV  HV  rV

=L by a factor of

N and exceeds the viscous force per unit volume, which is of order

rnV=L

, by a factor of Ha

which is often called the Chandrasekhar

number, particularly in the literature dealing with magnetoconvection

(see Magnetoconvection). Even though R

and Lu may be very small

in laboratory systems (see the Section on the imperfect conductor,

reconnection), Ha may be large because of the smallness of P

for

liquid metals; the Lorentz force can therefore profoundly affect the

motion. In large systems for which R

01, a more appropriate mea-

sure of J may be B=m

L, with a corresponding Lorentz force of order

L per unit volume. This is greater than the viscous force by order

N=P

and exceeds the inertial force by order 1=Al

, where Al is the

Alfvén number (also sometimes called the magnetic Mach number):

Al ¼V=V

: (Eq. 105)

It is frequently argued that an MHD system capable of generating its

own magnetic field will favor a dynamical balance in which inertial

and Lorentz forces are comparable ðAl ¼ Oð1ÞÞ so that the magnetic

and kinetic energies are comparable also: u

¼ Al

2

¼ Oð1Þ.In

a highly rotating system however, this is not necessarily true (see the

Section on the CMHD for imperfect fluids).

MHD boasts an analogue of the Proudman-Taylor theorem. This has

already been foreshadowed in the Section on the perfect conductor,

where an anisotropic friction was identified for R

 1 that acts to

damp out motions perpendicular to B in a time of order t

.If

 t

and t

, i.e., if Ha and N are so large that viscous and inertial

forces are negligible, the steady state form of Eq. (74) becomes

0 ¼ HðrPÞþJ  B; (Eq. 106)

which is the equation for magnetostatic equilibrium. Nevertheless,

because Ha  1, small motions create large enough currents to make

the Lorentz force significant in Eq. (106). Let B ¼ B

þ b, where B

is a uniform field applied across the system and bð B

Þ is the small

response to the flow. Then J ¼ j ¼ H  b=m

and Eq. (106) give

HJ ¼ 0: (Eq. 107)

If it is also true that R

 1 so that magnetic diffusion is negligible,

Eq. (73) and the steady induction equation (47) gives

MAGNETOHYDRODYNAMICS 649

HV ¼ 0: (Eq. 108)

The MHD two-dimensional theorem follows from Eqs. (107) and (108):

In a steady dissipationless MHD system across which a uniform

magnetic field is applied, the flow and current are two dimen-

sional with respect to the direction of the applied field.

Taking B

¼ B

, we have

V ¼ Vðx; yÞ; (Eq. 109)

J ¼ Jðx; yÞ: (Eq. 110)

This result may be compared with Eq. (89).

Solutions such as Eqs. (109) and (110), obtained on the assumption

that R

and R

are large, are subject to boundary conditions such as

½½nB ¼ 0; on the boundaries; (Eq. 111)

nV ¼ 0; on the boundaries; (Eq. 112)

cf. Eq. (80). Boundary layers are required to make the solutions satisfy

the full set of wall conditions; these are known as Hartmann layers. As

for the Ekman layer, the Hartmann layers are of a type sometimes

called “active” or “controlling,” since mainstream solutions involving

unknown functions, like Eqs. (109) and (110), cannot be completely

determined until certain “Stewartson conditions” that are demanded

by the Hartmann layer are applied:

1=2

½½n  V

¼ sgnðnBÞ½½n  B

r: (Eq. 113)

Here the unit normal n is directed from the boundary layer into the

fluid and the suffix bl signifies that the discontinuity is right across

the Hartmann layer, i.e., is the difference between mainstream and

boundary values; Eq. (113) is valid only where nB is nonzero.

In the limit of zero dissipation (n ! 0,  ! 0), the Hartmann layer

becomes a combined surface current C and surface vorticity Z, defined

in analogy to Eq. (14) as ½½nV ¼ Z. The origins of Eq. (113) can be

qualitatively understood as in the Section on the perfect conductor by

demanding that the viscous force associated with the shear generated

by the integrated Lorentz force, ðnBÞðnCÞ=m

, balances that force,

and by arguing that the emf created by Z is ðnBÞZ and generates C.

This also shows that the thickness of the Hartmann layer is of order

¼L=Ha ¼ðnÞ

1=2

What is perhaps most remarkable is that Eq. (113) applies even in

the absence of diffusion (n ¼  ¼ 0) but that nevertheless it depends

on the ratio P

of the two diffusivities! When B is nonuniform and

the boundaries are curved, H

 C is generally nonzero, so that the Hart-

mann layer pumps current into or out of the mainstream (see Eq. (18)).

The MHD two-dimensional theorem has implications for thermal

convection resembling those that the Proudman-Taylor theorem has

for rotating convection (see the Section on the Classical theory of

rotating fluids). Consider a Bénard layer, i.e., a uniform horizontal

layer of fluid, of depth L, heated from below and cooled from above.

Suppose a large uniform vertical field of strength B is applied

ðHa  1Þ.Ifn ¼ 0, weak motions must satisfy Eq. (109); by

Eq. (112), they are horizontal everywhere and therefore have no z-

component to carry heat across the layer. Convection can occur only

if the buoyancy force is large enough to break the magnetic constraint

of the two-dimensional theorem. Thus, although Ra

would be O(1) if

Ha were O(1), the critical Rayleigh number is large when Ha  1; in

fact Ra

¼ OðHa

Þ, and the (horizontal) scale L

of the motions perpen-

dicular to B

is OðHa

1=2

LÞ. If the applied field is horizontal instead of

vertical, it has no effect on the marginal mode, in which the pattern of

convection consists of horizontal rolls parallel to B

, for which the two

dimensional theorem applies, though now the two-dimensional motions

have a vertical component that transports heat across the layer. (See

Magnetoconvection.)

CMHD for ideal fluids

In a way reminiscent of MHD itself (see the Introduction), the combi-

nation of the classical theories of MHD and rotating fluids gives rise to

new phenomena that are absent from the two subjects in isolation. The

subject becomes so different that it deserves its own name and acro-

nym. The obvious choice, RMHD, has already been appropriated by

both “relativistic MHD” and “reduced MHD,” so it is called here “Cor-

iolis magnetohydrodynamics” or “CMHD.” Phenomena in which dif-

fusion plays a central role will be described in the Section on the

CMHD for imperfect fluids. Here we focus on ideal flows and, to illus-

trate as dramatically as possible how different CMHD is from MHD,

we shall suppose that the magnetic Rossby number,

¼V

=OL; (Eq. 114)

is small:

 1: (Eq. 115)

In the Earth’s core, Ro

¼ Oð10

3

Þ.

One of the ways in which the magnetic field transforms the classical

theory of rotating fluids is by removing the geostrophic degeneracy of

the inertial waves discussed in the Section on the Classical theory of

rotating fluids. These are replaced by a discrete set of torsional waves

(see Oscillations, torsional). These arise because the geostrophic cylin-

ders sketched in Figure M151 are coupled together by the s-component

of B, i.e., the component that threads the cylinders together. It was seen

in the Section on the Classical theory of rotating fluids that the Coriolis

force associated with geostrophic motions can be absorbed into the pres-

sure gradient. Since this otherwise dominating force is then essentially

absent, the remaining forces become influential, including the inertial

term r]

V. The torsional waves therefore resemble Alfvén waves and

have the same timescale, t

¼L=V

, where V

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

is now

based on the rms strength of B

on the geostrophic cylinder CðsÞ:

rhV

iðs; tÞ¼hB

iðs; tÞ¼

AðsÞ

CðsÞ

ðs; f; z; tÞdS:

(Eq. 116)

Even if

ﬃﬃﬃﬃﬃﬃﬃﬃﬃ

were as small as 10

3

T, the Alfvénic timescale t

less than a decade. This may be compared with the timescale of the

ageostrophic waves which (see below) is of order 10

y. It is also short

in comparison with the timescales, t

spin up

and t



, of the diffusive pro-

cesses. The high frequency character of the torsional waves means that

in describing them we may ignore the time-dependence of hB

i and all

diffusive effects.

The dissipationless geostrophic component of V obeys the inviscid

form of Eq. (98), now written as

¼hðJ  BÞ

i; (Eq. 117)

and by the induction equation (61) for a perfect conductor. (The term

2OhV

i has been omitted from Eq. (117) because of mass conserva-

tion; see Eq. (99).) In a steady state, hðJ  BÞ

i¼0, i.e.,

CðsÞ

ðJ  BÞ

dS ¼ 0: (Eq. 118)

This important result, due to Taylor (1963) defines what are called

Taylor states (see Taylor’s condition).

650 MAGNETOHYDRODYNAMICS

If Eq. (118) does not hold initially, a torsional wave is launched in

which the geostrophic cylinders oscillate about a Taylor state, V

ðsÞ.

Denoting by vðs; tÞ¼

ðs; tÞV

ðsÞ the departure of the geos-

trophic state from this Taylor state, Braginsky (1970) showed that

the associated shear z ¼ v=s satisfies the torsional wave equation

]

AhV



: (Eq. 119)

The waves transport the z-component, rs

, of the angular momen-

tum density to and fro across the core, but do not change the integrated

angular momentum of core flow:

M ¼

SIC

rsV

dV ¼ r

Ads: (Eq. 120)

In the simplest application of Eq. (119), the existence of the SIC is

ignored. The ordinary differential equation obtained by substituting

zðs; t Þ¼Zðs ÞexpðiotÞ into Eq. (119) has regular singularities at both

s ¼ 0 and s ¼ R

where A ¼ 0. The implicit requirement that Z be

bounded at both these points transforms Eq. (119) into an eigenvalue

problem for the torsional wave frequencies, o.

The picture is complicated by the SIC. This has a composition simi-

lar to the FOC but, being a solid, its conductivity is even greater and

the justification for ignoring its resistivity is even stronger. Since

ohmic and viscous diffusion are absent, the boundary layer at the

ICB is of Hartmann type (see the Section on Classical MHD) so that

Eq. (113) applies and P

is involved. Since however P

 1, the con-

dition (113) reduces to ½½B ¼ 0. In consequence,

z ¼ O

SIC

; for s < R

: (Eq. 121)

In other words, in torsional wave motion, the entire contents of the

tangent cylinder C

, both solid and liquid, move together as a solid

body. (For an alternative point of view, see Jault and Légaut, 2005.)

As Buffett (1996) showed, this part of the torsional motion is mainly

determined by the gravitational couple exerted by the mantle on the

SIC and by the EM torque on C

, which can be computed from

Eq. (43). As in the Section on the Basic equations, the simplified con-

dition O

SIC

¼ 0 is adopted here. The torsional waves therefore exist

only outside the tangent cylinder and the appropriate condition of

wave reflection at C

is zðR

Þ¼0.

If viscous and ohmic dissipation is allowed for, it is plausible that

the torsional waves will die out, so returning the system to the Taylor

state,

. Roberts and Soward (1972) demonstrated that viscosity

would quench the waves on the spin-up timescale, but over such a

long period the evolution of B, and therefore of

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

, would be

significant and the coefficients in Eq. (119) would change secularly.

It is plausible that ohmic dissipation in the fluid and in the mantle

(assumed weakly conducting) will quench the waves even more

rapidly on the t



timescale of the core, or perhaps (since it differs less

from t

) on the even shorter t



timescale of the mantle.

Electromagnetic coupling, either directly across the CMB, or indir-

ectly via the inner core with the gravitational coupling between the

mantle and inner core acting as catalyst (Buffett, 1996), provides one

of three ways in which angular momentum can be exchanged between

the core and the mantle, the other two being topographic coupling,

which depends on the roughness of the CMB, and viscous coupling,

which is generally thought to be negligibly small. Since the total angu-

lar momentum of the Earth is unchanged by such internal processes, a

correlation should exist between variations in the length of the day and

changes in the angular momentum of the core. Jault et al. (1988) were

the first to establish such a connection. From an analysis of the geo-

magnetic record they could trace the evolution of the core’s angular

momentum and could show that it was in antiphase with the mantle’s

angular momentum.

The excitation of torsional oscillations is inexplicable according to

the ideas presented here but it seems clear that it must be due to some

other higher frequency processes in the core, such as turbulence. For

further analysis see Jault (2003), Oscillations, torsional; Core-mantle

coupling, electromagnetic; Core-mantle coupling, gravitational; and

Core-mantle coupling, topographic. Bloxham et al. (2002) have asso-

ciated torsional waves with the observed secular variation “impulses”

(see Geomagnetic jerks).

Consider next the ageostrophic waves. When Ro

¼ Oð1Þ, the

waves are an inextricable mixture of inertial and Alfvén waves, but

when Eq. (115) holds, little remains of the Alfvén wave! This illus-

trates again how Coriolis forces can transform classic MHD. When

 1, the inextricable mixture neatly separates into two families:

inertial waves and slow waves, also known as “Lehnert waves.” The

former differ little from the inertial waves discussed in the Section

on the Classical theory of rotating fluids; they are “fast,” since their

timescale is diurnal. The latter are very unlike Alfvén waves. They

are called “slow” because their timescale, t

¼ OL

, is of order

y. This is comparable with the timescale of the secular variation

of the main geomagnetic field (see Geomagnetic secular variation).

The corresponding velocity, c

¼L=t

¼V

=OL, is of order

4

1

, which the speed at which discernable magnetic features

at the CMB drift westward. The time dependence of the slow waves

is governed by the left-hand side, ]

B, of the induction equation

(61); the inertial forces in Eq. (74) play essentially no role. For this

reason the waves are sometimes called MC waves, to emphasize that

the essential ingredients governing their propagation are the magnetic

and Coriolis forces alone (and of course the pressure gradient). The

relative unimportance of the inertial waves suggests that MC waves

can be analyzed in a clearer way by discarding the inertial forces in

Eq. (74). If this is done, however, the torsional waves are filtered out

too. By retaining the key part of the inertial force as in Eq. (101), both

the torsional and MC waves are retained but the inertial waves are

removed (see also Magnetohydrodynamic waves).

MC waves, like inertial waves, are dispersive but possess abundant

helicity, making them potentially efficient components of a dynamo.

Although they have axisymmetric parts, they are characteristically

large-scale planetary waves, i.e., they are asymmetric and, if they have

finite amplitude, they create an emf

ðV

B

that drives a current J

that potentially can defeat Cowling’s theorem (see the Section on the

kinematic dynamo). They are, however, obliterated by ohmic diffusion

in traveling a distance of order c



¼ðV

=OÞL. Buoyancy forces

can prevent their demise. This provides a strong motivation for study-

ing MAC waves, which are MC waves modified by the insertion of

Archimedean (buoyancy) forces. As in the example discussed in the

Section on the Classical theory of rotating fluids, it may be expected

that, if buoyancy is strong enough, instability occurs. More specifi-

cally, instability occurs when the buoyancy frequency N is of order

=L, i.e., when the magnetic Rayleigh number, Ra

is O(1), where

¼ gabL

: (Eq. 122)

If we accept the estimate V¼OðgsDT =OÞ made in the Section on the

Classical theory of rotating fluids, we may rewrite Eq. (122) as

¼ OVL=V

¼V=c

: (Eq. 123)

From O ¼ 7  10

4

1

, V¼2  10

4

1

, L¼10

m, and

¼ 0:1ms

1

, we obtain Ra

¼ 1. This suggests that MAC wave

instability is relevant to core dynamics.

The simplest demonstrations of MAC waves and their instabilities

(Braginsky, 1964) assume that they infinitesimally perturb a uniform

applied field B

in a plane layer of fluid. Braginsky (1967) also studied

small amplitude MAC waves and instabilities in a spherical system

in which the imposed field B

is zonal. In this case the waves travel

in the f-directions with speeds of order c

. Braginsky (1964)

MAGNETOHYDRODYNAMICS 651

suggested that the geomagnetic secular variation and westward drift

are manifestations of MAC waves. Since c

and V are approximately

equal when Ra

¼ 1, it appears that our method (see Section on The

imperfect conductor, reconnection) of estimating V from the speed of

westward drift speed c

is defensible. MAC wave instability is, as in

the Section on the Classical theory of rotating fluids, a single spasm

of overturning. To maintain the waves continuously it is necessary to

invoke diffusion, and this (as will be seen in the Section CMHD for

imperfect fluids) is destabilizing.

CMHD for imperfect fluids

Although the core is rapidly rotating in the classical sense (E  1,

Ro  1), it is not rapidly rotating according to the criterion L  1

of CMHD, where L is the Elsasser number, a dimensionless parameter

that can be written in several equivalent ways:

L ¼

O

¼ Ha

E ¼





¼ Ro

Lu:

(Eq. 124)

Far from being small, the value of L in the core is better described by

L ¼ Oð1Þ: (Eq. 125)

Equation (125) defines the scale for strong fields:

B¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðrO=sÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðm

rOÞ

; in strong field regime :

(Eq. 126)

This, like the Elsasser number, is independent of the length scale L.

According to Eq. (126), J¼OðsVBÞ¼ OðV

ðsrOÞÞ, so that the

Lorentz force, J  B, is of order rOV, i.e., the Lorentz and Coriolis

force, 2V  V, are about equal in magnitude. This suggests that the

primary force balance in the core is between 2V  V and J  B.It

is often said that the fact that the magnetic compass needle points

approximately north proves that the Coriolis force dominates core

dynamics. This however is an oversimplification. The Coriolis force

has a preferred direction, that of V. To counter the rotational constraint

(see below), the magnetic field configures itself so that it and the

Lorentz force share the same preferred direction.

In the same way that R

¼ Oð1Þ numerically underestimates the

magnetic Reynolds number required for dynamo action (see Section

on the kinematic dynamo), it appears from the Section on Classical

MHD that Eq. (125) numerically underestimates L. Writing Eq. (122) as

¼ R

=L; (Eq. 127)

we see that marginal MAC wave instability ðRa

 1Þ requires that

L ¼ Oð100Þ. Numerical estimates bear this out: if we take

¼ 0:1ms

1

and  ¼ 2m

1

as before, we obtain L  100 from

Eq. (124), and B  0:01 T, rather than the 10

3

T given by Eq. (126).

Far from being rapidly rotating, the core is, according to this value of

L, slowly rotating. Equation (124) shows that the magnetic energy

density u

exceeds the kinetic energy density u

in the rotating frame

by a factor of order Al

2

¼ L=R

Ro  10

, assuming as before that

L  100, R

 100 and Ro  10

5

A striking way in which CMHD differs from the classical theories

of rotating and MHD flows is that the two-dimensional theorems of

those subjects are no longer so constraining. If Ha0E

1=2

, the Lorentz

force weakens the Proudman-Taylor constraint; if E9Ha

2

, the Cor-

iolis force weakens the MHD constraint. When Lð¼ Ha

EÞ is O(1),

both constraints have diminished force. This has very significant

consequences for CMHD convection. Suppose that the Bénard layer

of the Section on Classical MHD rotates about a vertical axis. It is found

that Ra

¼ OðE

1

Þ for E ! 0, instead of the Ra

¼ OðE

4=3

Þ for the

same rotating system when nonmagnetic (see the Section on Classical

theory of rotating fluids). The horizontal scale of motions is comparable

in the marginal state with the vertical scale L, in contrast to the Section

on Classical theory of rotating fluids where the length scale L

in direc-

tions perpendicular to V was found to be small, OðE

1=3

LÞ. The result

¼ OðE

1

Þ may be written as Ra

mod;c

¼ Oð1Þ,where

mod

¼ gabL

=Ok ¼ RaE (Eq. 128)

is the modified Rayleigh number, which is often used in preference to

Ra in CMHD convection studies. The fact that this, like L and L

,is

independent of n serves to emphasize how Lorentz forces completely

take over from viscous forces in breaking the Proudman-Taylor con-

straint when L ¼ Oð1Þ.

The Bénard example is the simplest to show how convection adapts

to changes in field strength. The convection pattern arranges itself to

provide the Lorentz force necessary to break the rotational constraint.

For example, if B

is horizontal and L is small, the convection pattern

in the marginal state consists of horizontal rolls that are perpendicular

to B

and not parallel as in the Section Classical MHD. For larger L,

the rolls counter the Coriolis force by becoming inclined to B

at an

angle that diminishes as L increases.

This approach to rotating magnetoconvection is so simple that it

borders on the simplistic. It ignores processes that may be significant

in a naturally occurring CMHD system: the effects of nonlinearity,

boundary curvature, velocity shear, self-generation of field, etc. In par-

ticular, it assumes that the magnetic field in which convection occurs is

given. One might wonder whether a dynamo, which is required to gen-

erate its own magnetic field, would expend more energy in doing so

than it saved by recouping its convective energy losses. This qualm

can be most easily allayed by investigating finite amplitude convection

in the Bénard layer, in the absence of the applied field B

Suppose Ra is progressively increased from zero. Convection does

not occur until Ra reaches its critical value, Ra

¼ OðE

4=3

Þ, for which

convective motions of horizontal scale L

¼ OðE

1=3

LÞ become possi-

ble. As Ra is enhanced, L

increases, V grows in amplitude and, at

another critical value Ra

of Ra, L

becomes OðE

1=6

LÞ and V becomes

OðE

1=6

=LÞ so that dynamo action occurs ðR

¼L

V= ¼ Oð1ÞÞ,

and supports a field of infinitesimal amplitude. As Ra increases further,

becomes larger as do Vand B, but the system remains in a weak field

state in which the Hartmann number is O(1), i.e., by Eq. (103),

B¼

ðm

rnÞ=L; in weak field regime: (Eq. 129)

Unaided by viscosity, the Lorentz force is still too weak to counter

the rotational constraint, but this becomes less and less true as the

imposed Ra is made larger still; L

increases toward L and B

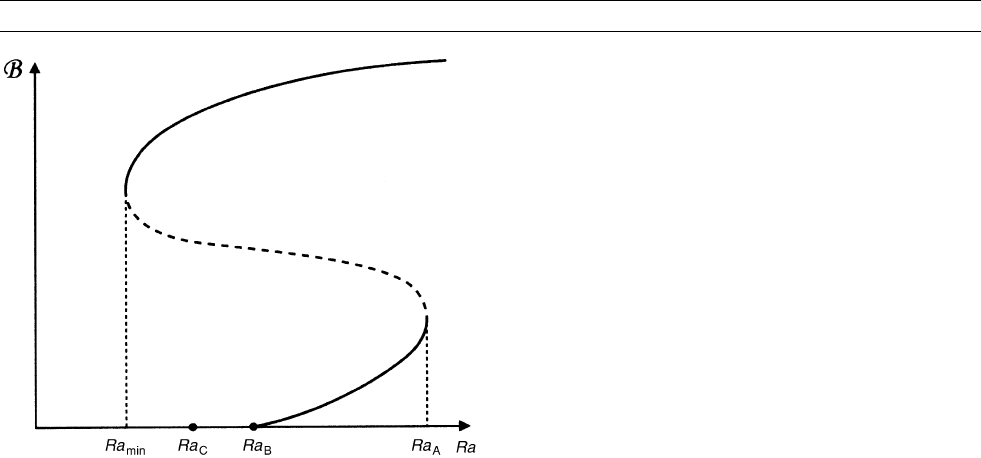
approaches an asymptote at Ra ¼ Ra

(see Figure M153). The weak

field regime exists only for Ra

< Ra < Ra

; it terminates at the

asymptote. As Ra increases to Ra

there is runaway field growth from

Ha ¼ Oð1Þ to the strong field regime where Ha ¼ OðE

1=2

Þ.

The scenario just described, apart from the final runaway process,

has been demonstrated by Soward (1974). His analysis showed that

the asymptote Ra ¼ Ra

exists. Strong field solutions were obtained

numerically by Jones and Roberts (2000). Once the strong field

dynamo is established, hysteresis occurs: the dynamo can continue to

function even if Ra is reduced below Ra

(Rotvig and Jones, 2002).

The dynamo is then in a “subcritical state.” It may even be that it

can regenerate the field when Ra < Ra

, but this has not been demon-

strated; it is clear however that the strong field branch is bounded

below by some value Ra

min

of Ra of order E

1

or larger, i.e., the

dynamo will fail if the buoyancy forces cannot make good the ohmic

losses.

It may be wondered whether the spherical convecting system con-

sideredintheSectiononClassicaltheory of rotating fluids would behave

in a fundamentally different way from the plane layer. This qualm is

significantly harder to allay because the analytical and numerical

652 MAGNETOHYDRODYNAMICS

approaches are much more difficult to implement. There seems, how-

ever, to be no reason to doubt that, by opposing the rotational con-

straint, a magnetic field will generally allow convection to occur on

large scales, as planetary waves, with correspondingly less ohmic

and viscous energy losses, and that a strong field branch of dynamo

solutions will result. Numerical simulations of convective dynamos

have demonstrated that the field adapts itself to oppose the Coriolis

force. They have also confirmed the increase in the scale, L

, created

by the magnetic field; far fewer Taylor cells lie on the cartridge belt of

the Section on Classical theory of rotating fluids. Through the analysis

of magnetic features on the CMB, Gubbins and Bloxham (1987) have

inferred flux concentrations that may be associated with the ends of

four, but no more than four, Taylor cells (see also Kahle et al., 1967).

In the parameter range just considered (E  1, P

¼ Oð1Þ,

¼ Oð1Þ), the criterion Ra

¼ Oð1Þ of the Section on CMHD for ideal

fluids for MAC wave instability is essentially the same (for L ¼ Oð1Þ)

as the criterion Ra

mod

¼ Oð1Þ for thermal instability. This range is

however irrelevant to the core, where E  1, P

¼ Oð1Þ, P

 1. It is

hard to make progress in this difficult parameter range, and the theory

is still somewhat speculative. Since Ra

=Ra

mod

¼ðP

ÞL

1

Oðk=Þ10

5

, thermal convection can occur in the range

1 < Ra

mod

< Ra

in which MAC wave instability is impossible. Since,

by Eq. (127), R

< L  100 in this range of Ra

mod

, convective motions

are too weak to maintain a dynamo. Only when the convection is

strongly supercritical and the MAC wave bifurcation is reached

(Ra

mod

 10

, Ra

 1) can magnetic field be generated. (For analo-

gous behavior in a simpler system, see Jones et al., 1976.)

The observed geomagnetic field shows a tendency to drift in longi-

tude (see Westward drift). Three mechanisms may contribute to this

motion: field diffusion, MAC wave propagation and actual fluid

motions. Field lines can diffuse with velocity c

¼ =L relative to

the moving conductor (see the Section on The imperfect conductor,

reconnection), and this velocity is comparable for R

¼ Oð1Þ with V

and c

. It is therefore hard to decide quantitatively how much of the

observed drift to attribute to each of the mechanisms. A CMHD model

of Roberts and Stewartson (1975) demonstrated a clear preference for

westward flux diffusion (see also Acheson, 1972). The recent geody-

namo simulations of Glatzmaier and Roberts (1997) have shown a

striking propensity for flux diffusion to the west despite zonal fluid

motion predominantly to the east.

As shown in the Sections on the Classical theory of rotating fluids

and Classical MHD, boundary layers arise when E  1 and also when

Ha  1. Another characteristic of CMHD is that, when Lð¼ Ha

EÞ is

O(1), neither Ekman nor Hartmann layers exist; they are replaced by a

composite Ekman-Hartmann layer. Its thickness, d

, is of the same

order as d

and d

. It pumps both fluid and current into or out of

the mainstream beyond the boundary layer. As for the Ekman and

Hartmann layers, the Ekman-Hartmann layer provides a link through

which angular momentum can be exchanged between the fluid and

surrounding solid walls. This is accomplished by a viscous stress and, if

the wall is electrically conducting, by a magnetic stress (see Eq. (39)).

The role of boundary layers in geomagnetic simulations has been

controversial (see Core, boundary layers).

Paul H. Roberts

Bibliography

Acheson, D.J., 1972. On the hydromagnetic stability of a rotating fluid

annulus. Journal of Fluid Mechanics, 52: 529–541.

Bloxham, J., Zatman, S., and Dumberry, M., 2002. The origin of geo-

magnetic jerks. Nature, 420:65–68.

Braginsky, S.I., 1964. Magnetohydrodynamics of Earth’s core. Geo-

magnetism and Aeronomy, 4 : 698–712.

Braginsky, S.I., 1967. Magnetic waves in the Earth’s core. Geomag-

netism and Aeronomy, 7: 851–859.

Braginsky, S.I., 1970. Torsional magnetohydrodynamic vibrations in

the Earth’s core and variations in day length. Geomagnetism and

Aeronomy, 10:1–8.

Braginsky, S.I., and Meytlis, V.P., 1990. Local turbulence in the Earth’s

core. Geophysical and Astrophysical Fluid Dynamics, 55:71–87.

Braginsky, S.I., and Roberts, P.H., 1995. Equations governing convec-

tion in Earth’s core and the Geodynamo. Geophysical and Astro-

physical Fluid Dynamics, 79:1–97.

Braginsky, S.I., and Roberts, P.H., 2003. On the theory of convection

in the Earth’s core. In Ferriz-Mas, A., and Núñez, M. (eds.), Advances

in Nonlinear Dynamos. London: Taylor & Francis, pp. 60–82.

Buffett, B.A., 1996. A mechanism for decade fluctuations in the length

of day. Geophysical Research Letters, 23: 3803–3806.

Busse, F.H., 1970. Thermal instabilities in rapidly rotating systems.

Journal of Fluid Mechanics, 44: 441–460.

Cowling, T.G., 1933. The magnetic field of sunspots. Monthly Notices

of the Royal Astronomical Society, 140:39–48.

Davidson, P.A., 2001.

An Introduction to Magnetohydrodynamics.

Cambridge, UK: Cambridge University Press.

Gill, A.E., 1982. Atmosphere-Ocean Dynamics. New York: Academic

Press.

Glatzmaier, G.A., and Roberts, P.H., 1997. Simulating the geodynamo.

Contemporary Physics, 38: 269–288.

Greenspan, H.P., 1968. The Theory of Rotating Fluids. Cambridge,

UK: Cambridge University Press.

Gubbins, D., and Bloxham, J., 1987. Morphology of the geomag-

netic field and implications for the geodynamo. Nature, 325:509–511.

Jault, D., 2003. Electromagnetic and topographic coupling, and LOD

variations. In Jones, C.A., Soward, A.M., and Zhang, K. (eds.), Earth’s

Core and Lower Mantle. London: T aylor & Francis, pp. 56–76.

Jault, D., and Légaut, G., 2005. Alfvén waves within the core. In

Soward, A.M., Jones, C.A., Hughes, D.W., and Weiss, N.O.

(eds.), Fluid Dynamics and Dynamos in Astrophysics and Geophy-

sics. Boca Raton, FL: CRC Press, pp. 277–293.

Jault, D., Gire, G., and Le Mouël, J.-L., 1988. Westward drift, core

motions and exchanges of angular momentum between core and

mantle. Nature, 333: 353–356.

Jones, C.A., and Roberts, P.H., 2000. Convection-driven dynamos in a

rotating plane layer. Journal of Fluid Mechanics, 404:311–343.

Jones, C.A., Moore, D.R., and Weiss, N.O., 1976. Axisymmetric con-

vection in a cylinder. Journal of Fluid Mechanics, 73: 353–388.

Figure M153 A cartoon showing the weak and strong field

branches of the plane layer dynamo (full lines). The dashed curve

displays the unstable branch connecting them (see text for full

explanation).

MAGNETOHYDRODYNAMICS 653

Jones, C.A., Soward, A.M., and Mussa, A.I., 2000. The onset of ther-

mal convection in a rapidly rotating sphere. Journal of Fluid

Mechanics, 405: 157–179.

Kahle, A.B., Ball, R.H., and Vestine, E.H., 1967. Comparison of esti-

mates of surface fluid motions of the Earth’ s core at various

epochs. Journal of Geophysical Research, 72: 4917–4925.

Krause, F., and Rädler, K.-H., 1980. Mean-field Magnetohydrody-

namics and Dynamo Theory. Oxford, UK: Pergamon Press.

Lehnert, B., 1954. Magnetohydrodynamic waves under the action of

the Coriolis force, Part I. Astrophysics Journal, 119: 647–654.

Parker, E.N., 1968. Hydromagnetic dynamo models. Astrophysics

Journal, 122: 293–314.

Roberts, P.H., 1968. On the thermal instability of a rotating-fluid

sphere containing heat sources. Philosophical Transactions of the

Royal Society of London Series A, 263:93–117.

Roberts, P.H., and Soward, A.M., 1972. Magnetohydrodynamics of

the Earth’s core. Annual Review of Fluid Mechanics, 4:117–152.

Roberts, P.H., and Stewartson, K., 1975. On double-roll convection in

a rotating magnetic system. Journal of Fluid Mechanics, 68:447–466.

Rotvig, J., and Jones, C.A., 2002. Rotating convection-driven dyna-

mos at low Ekman number. Physical Review E, 66: 056308.

Soward, A.M., 1974. A convection-driven dynamo. I. Weak-field case.

Philosophical Transactions of the Royal Society of London Series

A, 275:611–651.

Taylor, J.B., 1963. The magnetohydrodynamics of a rotating fluid and

the Earth’s dynamo problem. Proceedings of the Royal Society of

London Series A, 274: 274–283.

Tilgner, A., 2005. Precession driven dynamos. Physics of Fluids , 17:

034104.

Cross-references

Alfvén Waves

Alfvén, Hannes Olof Gösta

Alfvén’s Theorem and the Frozen Flux Approximation

Anelastic and Boussinesq Approximations

Antidynamo and Bounding Theorems

Convection, Nonmagnetic Rotating

Core Turbulence

Core, Adiabatic Gradient

Core, Boundary Layers

Cowling’s Theorem

Dynamo, Backus

Dynamo, Braginsky

Dynamo, Bullard-Gellman

Dynamo, Gailitis

Dynamo, Herzenberg

Dynamo, Ponomarenko

Dynamos, Experimental

Dynamos, Fast

Dynamos, Kinematic

Dynamos, Mean Field

Dynamos, Periodic

Geodynamo

Geodynamo, Energy Sources

Geodynamo, Numerical Simulations

Geodynamo, Symmetry Properties

Geomagnetic Jerks

Geomagnetic Secular Variation

Harmonics, Spherical

Inner Core Rotational Dynamics

Inner Core Tangent Cylinder

Magnetohydrodynamic Waves

Oscillations, Torsional

Proudman-Taylor Theorem

Taylor’s Condition

Thermal Wind

Westward Drift

MAGNETOMETERS, LABORATORY

Magnetometers in paleomagnetic laboratories are used for the determi-

nation of the geomagnetic field directions and intensities that have

been recorded in rocks, and also for the discrimination of magnetic

minerals and their magnetic properties. For paleomagnetism, the main

consideration is to measure that magnetization vector in a rock,

whereas for environmental magnetism the requirement is to identify a

sample’s magnetic mineralogy and grain size distribution. In either case

the magnetometers employed can operate by one of two fundamentally

different processes. Either the magnetization of the sample can be used

to induce a current in a sensing coil, or the magnetization can create

a force by interacting with an instrument-generated magnetic field

gradient, and the force measured by a variety of methods.

Magnetometers used for determination of

paleomagnetic vectors

Standard paleomagnetic samples are 2.5 cm diameter cores, approxi-

mately 2.5 cm in length, and most paleomagnetic magnetometers will

be designed for this sample size. The major exception of this will be

whole core sections commonly collected from lake and deep-sea

sediments and used in environmental studies. These cores are typically

10 cm in diameter and can be several meters in length.

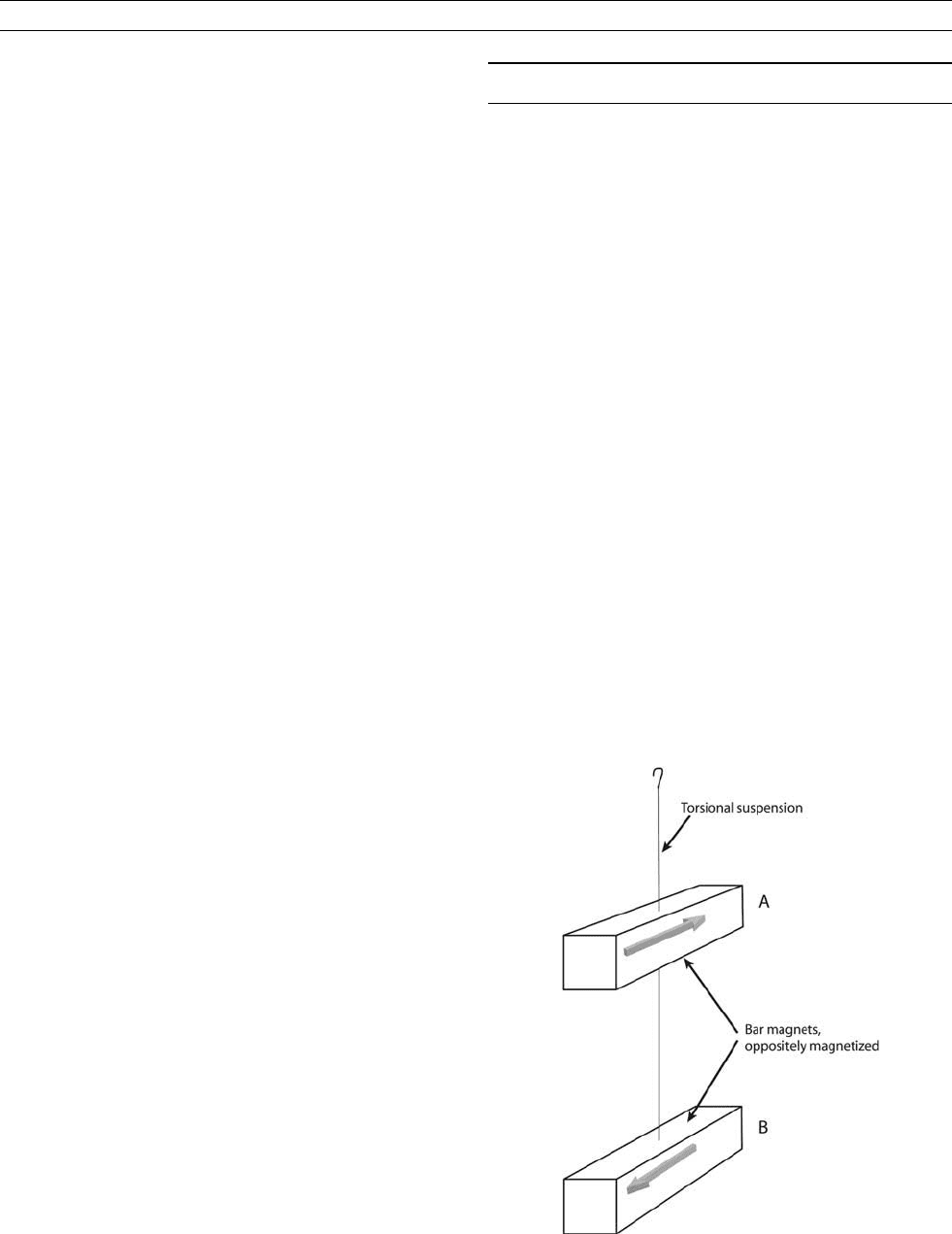
Astatic magnetometers

Astatic magnetometers were the most common type of instrument in

paleomagnetic laboratories in the 1950s and 1960s. They are a force-

type magnetometer, where the magnetization of a sample is used to

exert a force on a pair of identical suspended magnets. The bar

magnets are set with their axis horizontal and are suspended vertically

above each other via a torsional wire (Figure M154). Although in

Figure M154 The arrangement of magnets in an astatic

magnetometer. If sample is either placed in the horizontal

plane containing magnet B, or vertically below B, then only

the magnetization component normal to that of B is measured.

If the sample is placed midway between A and B, then the

vertical component of its magnetization is measured.

654 MAGNETOMETERS, LABORATORY

principle, just one magnet could be used, the vertical pairing of the

magnets increases accuracy by making the deflection insensitive to

uniform field gradients. Addition of a third magnet (parastatic magnet-

ometers) reduces sensitivity to changes in vertical field gradients. The

accuracy of astatic magnetometers largely depends on the magnets

having a large magnetization and small moment of inertia, but typi-

cally sensitivities are less than 10

–8

. One of the first such instru-

ments was used for paleomagnetism by Blackett (1952) and similar

instruments were in common usage in paleomagnetic laboratories into

until the mid-1970s.

Spinner magnetometers

These are a range of magnetometers that induce a signal in a static sen-

sor by spinning the sample about its own axis. The spinning sample

will produce a time-varying magnetic flux with respect to one or more

stationary sensors. The sensor determines the magnetization compo-

nent in the plane normal to the sample rotation axis. Within this plane,

the magnetization vector is found with reference to a fixed direction by

comparing the sensor output to a signal linked to the rotation mechan-

ism (Collinson, 1983). The overall sensitivity of the spinner magnet-

ometer will depend on the speed at which the sample is rotated and

the sensitivity of the sensors themselves, and so a wide range of sensi-

tivities are possible depending on the type of sensor employed. The

simplest sensor is an induction coil placed around the sample chamber,

and in this case the signal output will increase with sample size

(limited by the induction coil size) and with the rotation frequency.

The highest sensitivities for such instruments approach 10

–10

Fluxgate sensors (see Observatories, instrumentation) may be used

instead of induction coils or increased sensitivity can be obtained using

a superconducting quantum interference device (SQUID) detector (see

Cryogenic magnetometers below).

Cryogenic magnetometers (see also Rock

magnetometer, superconducting)

Cryogenic magnetometers are currently the most sensitive device for mea-

suring magnetizations, commonly achieving sensitivities of 10

–12

They consist of a superconducting coil that surrounds the sample to be

measured. The magnetizationof the sample changes the magnetic flux that

passes through the sensing coil, which then induces a current to flow

through the sensor coil. The current is detected by a SQUID, and these

magnetometers are sometimes referred to as SQUID magnetometers.

There are two types of SQUIDs, direct current (DC) and radio frequency

(RF), depending on the exact method used to detect the current induced

in the sensing coil. DC SQUIDs are more expensive but much more

sensitive, and it is this type that is usually used in modern paleomagnetic

magnetometers.

SQUID magnetometers can only measure the change in magnetic

flux through its sensing coils, and there will be an output signal even

when no sample is present. Thus, in order to determine a sample’s

magnetization, it must be cycled in and out of the sensing coil and

the background reading subtracted.

The main disadvantage of cryogenic magnetometers is the requirement

of having to keep the sensing coil superconductive, since this normally

requires immersion in liquid helium (recently 4.2 K cryocoolers have been

used without the need of liquid helium). High-temperature SQUIDs are

able to operate at liquid nitrogen temperatures but the increased ther-

mal noise prevents then from attaining the sensitivities available for

conventional SQUIDs.

Magnetometers used for discrimination of

magnetic minerals

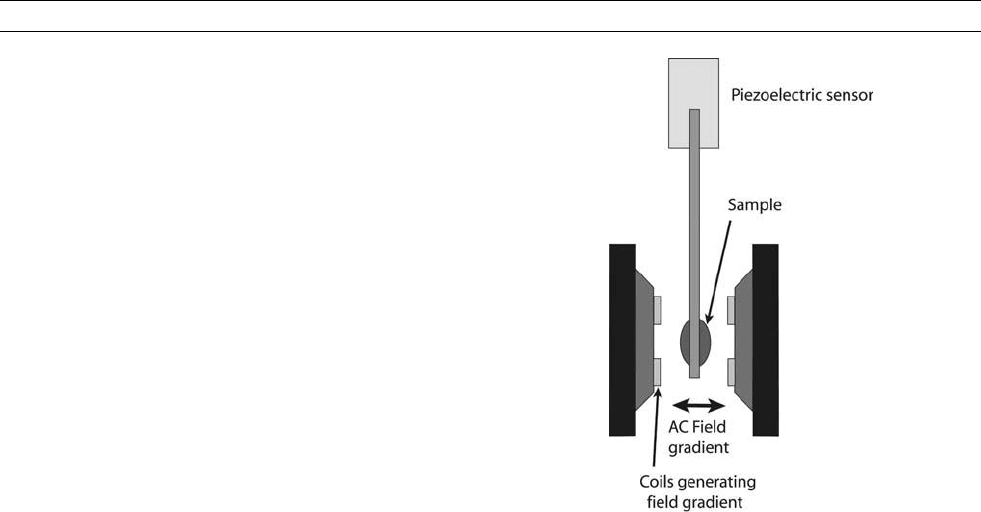
Alternating gradient magnetometers (AGM)

Electromagnets are used to produce an alternating magnetic field gradi-

ent across a region in which a sample is placed. The sample is mounted

at one end of a vertical cantilever, the other end of which is attached

to the bottom of a piezoelectric transducer (see Figure M155). The

alternating field gradient exerts an oscillatory force on the sample, and

the bending of the transducer produces a voltage proportional to the

amplitude of the oscillation.

The amplitude of the displacement of the rod at the sample is then

given by A ¼ M · ∇H (Q /k), where M is the sample magnetization,

∇H is the field gradient generated by the instrument, Q is the mechan-

ical quality factor of the cantilever (its resonance frequency divided by

its resonance width), and k is the effective spring constant of the rod.

The AGM needs to be operated at the resonance frequency of the

cantilever system, and this will change with the weight of the sample.

The sensitivity of the instrument is limited by thermal noise in the

mechanical oscillator, and typical sensitivities are comparable to

cryogenic magnetometers (10

–12

A DC field may also be applied during measurements, allowing the

magnetization as a function of field to be determined. Often a heater or

cryostat is also fitted to such instruments allowing both field and tem-

perature variation of the magnetization to be determined (O’Grady

et al., 1993).

AGMs are not well suited to measuring paleomagnetic samples since

they only measure the magnetization component along the applied field

gradient, and the sample size is relatively small (usually a few milli-

meters in size) compared with the standard paleomagnetic sample size

of 2.5 cm diameter cores. AGMs are good for characterization of

magnetic minerals and determining the magnetization dependence as a

function of applied field or temperature.

Vibrating sample magnetometers

These are similar to AGMs, but rather than using a field gradient, the

sample is mechanically vibrated at a fixed frequency (see Figure M156).

The sensing coils will have an emf induced within them due to

the changing flux produced by the vibrating sample. For a sample

magnetization M, the induced voltage V in the sensing coils is given

by V ¼ m

GMoA sin ot, where o is the angular frequency of the

vibration, and A is the vibration amplitude. G is a factor relating to the

geometry of the sensing coils. A uniform magnetic field in the region

Figure M155 A schematic of an alternating gradient magnetometer.

The force on the sample is generated by a set of field coils, and the

motion of the sample is proportional to its magnetization.

MAGNETOMETERS, LABORATORY 655