Gubbins D., Herrero-Bervera E. Encyclopedia of Geomagnetism and Paleomagnetism

Подождите немного. Документ загружается.

Type IV: Magnetically driv en MAC waves

When the magnetic field becomes sufficiently strong or complex, then

MC/MAC waves can be produced by either diffusive (resistive) or

ideal instability of the background magnetic field. The resulting waves

are of diffusive MC/MAC or diffusionless MC/MAC type and propa-

gate on either the magnetic diffusion or on the MC/MAC timescale.

They do not require the presence of buoyancy for their existence,

and can even occur when the background density field is stable.

Fearn and Proctor (1983) have considered the additional effect of

the presence of a background azimuthal flow (including shear) and

found that this tends to stabilize diffusive MAC waves. They observed

that such waves are localised at the extrema of the shear, moving with

an azimuthal speed equal to the fluid velocity at that point. This indi-

cates MC/MAC waves could perhaps be preferentially excited in zonal

jets and would drift by advection rather than propagation, which could

perhaps be of relevance at low latitudes in the Earth’s outer core (see

the section “Magnetohydrodynamic Waves as a Mechanism for Geo-

magnetic Secular Variation”).

Nonlinear magnetohydrodynamic waves

All the magnetohydrodynamic waves discussed up to now have been

linear in nature. This implies that (i) waves can simply be superposed

without considering any mutual interaction and (ii) there is no feed-

back between the waves and the rest of the system. This scenario is

unphysical because unstable waves can grow without limit, but is

nonetheless useful for determining the types of waves most easily

excited in a particular regime of interest. Early studies by Braginsky

(1967) and Roberts and Soward (1972), though deriving linear equa-

tions for MAC waves riding on general background states, emphasized

the importance of understanding nonlinear feedback processes. They

noted that waves are determined by the background state, but the back-

ground state is itself altered by the waves. In seeking to interpret geo-

physical observations indicative of hydromagnetic waves in the

Earth’s core, we should remember that linear analysis is only formally

valid for small perturbations to an artificial, steady background state

and cannot tell us how waves will evolve, saturate, interact with each

other, or what flow structures migh t result from nonlinear bifurcations

of the waves. Attempts to understand such processes deserve a con-

certed theoretical and numerical modeling effort in the future.

Some progress in understanding nonlinear MAC waves has already

been made. El Sawi and Eltayeb (1981) have derived higher order

equations for MAC waves in a plane layer in the presence of a slowly

varying background mean flow. Their equations describe the evolution

of diffusionless MAC wave amplitude via the conservation of wave

action (wave energy divided by wave frequency per unit volume). This

conservation law tells us that wave energy increases, at the expense of

the energy of the background state, whenever a wave moves into a

region where its frequency is higher. More recently Ewen and Soward

(1994) have derived equations describing the evolution of the ampli-

tude of diffusive MAC waves in the limit of a weak magnetic field.

They find that an azimuthal (geostrophic) mean flow is driven by mag-

netic forces resulting from the MAC waves and is linearly damped by

viscous diffusion at the boundary.

A start has also been made at numerically investigating the non-

linear evolution of magnetohydrodynamic waves in rapidly rotating,

convecting spherical shells. As the unstable density gradient is

increased, it is observed that the system undergoes bifurcations from

steadily traveling magnetohydrodynamic waves to vacillating wave

motions for which both temporal and spatially symmetries have been

broken (see Magnetoconvection).

Study of nonlinear MC and MAC waves is still in its infancy and

may yet yield important and exciting insights that will help us to better

understand how magnetohydrodynamic waves might manifest them-

selves in the Earth’s core.

Magnetohydrodynamic waves in a stratified

ocean at the core surface?

There has been some debate over the possibility of a stratified layer or

“inner ocean” at the top of the Earth’s outer core and the MAC waves

that would be supported there (Braginsky, 1999). This stratified layer

has yet to be observed seismically, though its existence seems plausi-

ble on thermodynamic grounds with light fluid released during

the solidification of the inner core expected to pond below the core-

mantle boundary. Oscillations of such a layer would be of shorter

period than the MC/MAC waves expected in the body of the outer

core due to the presence of an additional restoring force due to density

stradification.

The dynamics of a stably stratified layer would be dominated by its thin

spherical shell geometry. There would undoubtedly be many similarities

with the water ocean on the Earth’s surface, but with the additional com-

plications caused by the presence of magnetic forces. In particular, MC

Rossby waves, which rely on the change in the Coriolis force with latitude

for theirexistence, are likelyto be present withinsuchan ocean.Braginsky

has developed models of both axisymmetric and nonaxisymmetric

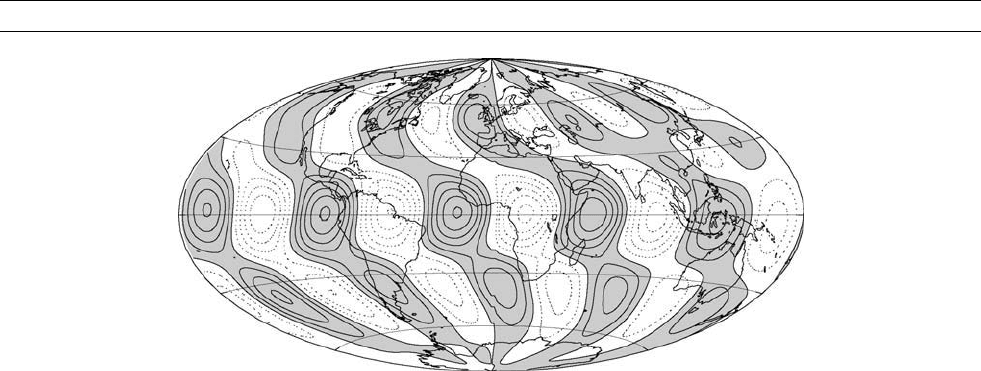
Figure M148 Anomalies in the radial magnetic field (B

)atr ¼ 0:95r

produced by a marginally critical, m ¼ 5, buoyancy-driven

magneto-Rossby wave. The imposed magnetic field is purely toroidal and increases linearly in magnitude with distance from the

rotation axis. Units are arbitrary because no nonlinear saturation mechanisms are included in this model. Gray regions with solid

contours indicate negative field anomalies, and white regions with dotted contours indicate positive field anomalies.

636 MAGNETOHYDRODYNAMIC WAVES

disturbances of such a stably stratified layer and has suggested they could

be responsible for short period geomagnetic secular variation.

Unfortunately, MAC waves and MC Rossby waves in a hidden

ocean at the top of the outer core are not the only possible source of

short period geomagnetic secular variation-torsional oscillations within

the body of the core (see Oscillations, torsional) are an equally plau-

sible explanation. Until the existence of the hidden ocean of the core

can be confirmed, study of magnetohydrodynamic waves that may

exist there will remain of primarily theoretical interest.

Magnetohydrodynamic waves as a mechanism

for geomagnetic secular variation

It has been common knowledge since the time of Halley that the

Earth’s magnetic field changes significantly over decades to centuries.

Perhaps the most striking aspect of this geomagnetic secular variation

is the westward motion of field features (see Westward drift). Several

explanations have been proposed for this Westward drift, but today there

are two widely accepted candidate mechanisms. The first involves bulk

fluid motion at the surface of the outer core that advects magnetic field

features. Bullard et al. (1950) originally envisaged this involving west-

ward flow of all the fluid close to the core surface, but modern core flow

inversions (see Core motions) have refined this suggestion—it now

appears that a westward equatorial jet under the Atlantic hemisphere is

sufficient to explain much of the westward drift of the geomagnetic field

observed at the surface. The source of this proposed equatorial jet is still

debated, but geodynamo models indicate that it could be produced by

nonlinear inertial forces that are a by-product of columnar convection

in a sphere, or by thermal winds due to an inhomogeneous heat flux into

the mantle (see Inhomogeneous boundary conditions and the dynamo).

The second possible mechanism is that motivating the inclusion of this

article in an Encyclopedia of Geomagnetism and Paleomagnetism—

propagation of magnetohydrodynamic waves in the Earth’s outer core.

We shall henceforth refer to this mechanism as the wave hypothesis.

Hide (1966) and Braginsky (1967) proposed the wave hypothesis on

theoretical grounds and each attempted to test it through the considera-

tion of available records of the geomagnetic secular variation. It is

informative to review these pioneering attempts before considering

other possible ways to search for the presence of magnetohydrody-

namic waves in the Earth’s outer core.

Hide (1966) identified three major factors in favor of the wave

hypothesis: (i) MC waves had periods comparable with the timescale

of geomagnetic secular variation; (ii) MC waves had dispersion times

comparable with the timescale of geomagnetic secular variation; and

(iii) shorter wavelength MC waves had larger phase velocities and

similarly higher order spherical harmonic components of the geomag-

netic field drifted faster. His observational analysis was based on

the mean westward drift rates of spherical harmonics up to degree 4,

from seven previous publications, spanning 135 years from 1830 to

1965. Despite the failure of detailed comparisons between the pre-

dicted and observed drift rates for individual spherical harmonics,

this study was instrumental in persuading many geophysicists that a

wave origin for geomagnetic secular variation was worth serious

consideration.

Braginsky (1967, 1972, 1974) sought to confirm the wave hypothesis

by comparing his own theoretical predictions of the spectrum of diffusion-

less MAC waves to an observationally inferred spectrum of geomagnetic

secular variation. Despite the poor quality of data available in the early

Figure M149 Equatorial time-longitude plot of processed radial magnetic field B

(with time-averaged axisymmetric field and field

variations with timescales longer than 400 years removed) from the historical field model gufm1, (Jackson et al., 2000). Field evolution

in the azimuthal direction at the equator is shown and consists of spatially and temporally coherent wavelike anomalies, with dominant

azimuthal wave number m ¼ 5 and moving consistently westward. The contour lines are at intervals of 5  10

nT. Gray regions with

solid contours indicate negative field anomalies, and white regions with dotted contours indicate positive field anomalies.

MAGNETOHYDRODYNAMIC WAVES 637

1970s, Braginsky’s efforts were important in demonstrating that the wave

hypothesis was at least compatible with observations.

In the last 20 years there have been significant advances in our

observational knowledge of the Earth’s magnetic field and its evolu-

tion. Using over 365000 historical observations from maritime

records, observatories, surveys, and satellites, time-dependent models

of the global magnetic field have now been constructed covering

the past 400 years (see Time-dependent models of the geomagnetic

field). Use of regularised inversion methods has enabled the

construction of images of the magnetic field at the core surface

allowing us to map its evolution at the edge of the source region.

This technique has shown that the origin of the westward drift of

magnetic field is not due to the whole field drifting westward but

rather is due to the drift of small patches of intense magnetic field

(see Westward drift), particularly at low latitudes in the Atlantic hemi-

sphere. Advances have also been made in our understanding of field

evolution over longer time intervals, notably through the use of archeo-

magnetic and lake sediment records to construct global field models

for the past 3 ka (Korte and Constable, 2005). Although lacking

the resolution of the historical models, these models offer the first

glimpse of the long-term behavior of flux patches at the core surface

and with the inclusion of more data hold great promise for the future.

Can recent observational advances help us in our attempts to evalu-

ate the wave hypothesis by facilitating the identification of previously

obscured signatures of magnetohydrodynamic waves? The existence

of images of the evolution of the field at the core surface opens

up fresh possibilities for comparing not only timescales of predicted

wave motions, but also geographical features such as the latitude at

which waves occur, their equatorial symmetry and their dispersive

properties. Space-time analysis of geomagnetic field evolution, and

particularly the use of time-longitude diagrams (as employed by ocea-

nographers to study Rossby waves), can be carried out during the his-

torical epoch (Finlay and Jackson, 2003). As shown in Figure M149,

after the removal of the time-averaged axisymmetric field and those

components of the field varying on timescales longer than 400 years,

spatially and temporally coherent (wavelike) evolution of the radial

magnetic field is observed at the equator. The clearest signal in the

time-longitude plot has an azimuthal wave number of m ¼ 5, a period

of around 250 years and travels at 17 km yr

1

westwards . Figure M150

shows the result of frequency-wave number filtering to recover the

spatial structure of this wave at the core surface. The domination

of aspects of geomagnetic secular variation by a single wave number

disturbance suggests that a magnetohydrodynamic wave (perhaps

driven by an instability) might currently be present at low latitudes

in Earth’s outer core.

The major challenge for theoreticians is to keep pace with improving

observations and construct models accurate enough to predict the structure

of observable space-time features caused by magnetohydrodynamic

waves in the core. Modeling of convection-driven magnetohydrodynamic

waves (see Magnetoconvection) suggests these might propagate too

slowly to account for observed azimuthal field motions. However, thermal

and magnetic winds in the core (see Thermal wind) could advect wave

patterns at the required speeds and produce spatially and temporally

coherent patterns of field evolution consistent with observations.

The hypothesis that magnetohydrodynamic waves produce directly

observable changes in the geomagnetic field cannot yet be conclusively

confirmed or rejected. The difficulty in rigorously testing the hypothesis

is twofold. Firstly, one requiresrobust predictions of observablesignatures

from theoretical wave models that take account of realistic background

fields, diffusion, spherical geometry, and nonlinearity. Secondly, one

requires self-consistent, high-fidelity observations over a long period of

time to assess model predictions in a statistically significant way. Almost

40 years after the wave hypothesis was proposed this remains a tall order,

but we are approaching the stage where such tests will be feasible.

Christopher Finlay

Bibliography

Acheson, D.J., 1972. On hydromagnetic stability of a rotating fluid

annulus. Journal of Fluid Mechanics, 52: 529–541.

Acheson, D.J., and Hide, R., 1973. Hydromagnetics of rotating fluids.

Reports on Progress in Physics, 36: 159–221.

Alfvén, H., 1942. Existence of electromagnetic-hydrodynamic waves.

Nature, 150: 405–406.

Braginsky, S.I., 1964. Magnetohydrodynamics of the Earth’score.

Geomagnetism and Aeronomy, 4:898–916 (English translation,

698–712).

Braginsky, S.I., 1967. Magnetic waves in the Earth’s core. Geomagnet-

ism and Aeronomy, 7:1050–1060 (English translation, 851–859).

Braginsky, S.I., 1972. Analytical description of the geomagnetic field

of past epochs and determination of the spectrum of magnetic

waves in the core of the Earth. Geomagnetism and Aeronomy,

12: 1092–1105 (English translation, 947–957).

Braginsky, S.I., 1974. Analytical description of the geomagnetic field

of past epochs and determination of the spectrum of magnetic

Figure M150 Snapshot from 1830 of the m ¼ 5 radial magnetic field, core surface signal responsible for the wavelike pattern of field

evolution observed at low latitudes in the historical geomagnetic field model gufm1. This snapshot was obtained by restricting the

period of field variations to between 125 and 333 years and the wave number of field variations to m ¼ 5 (i.e., FK filtering). The contour

lines are at intervals of 4  10

nT. Gray regions with solid contours indicate negative field anomalies, and white regions with dotted

contours indicate positive field anomalies.

638 MAGNETOHYDRODYNAMIC WAVES

waves in the core of the Earth. II. Geomagnetism and Aeronomy,

14: 522–529 (English translation, 441– 447).

Braginsky, S.I., 1989. Magnetohydrodynamic waves within the Earth.

In James, D. E. (eds.), Encyclopedia of Solid Earth Geophysics.

Kluwer Academic Publishers.

Braginsky, S.I., 1999. Dynamics of the stably stratified ocean at the

top of the core. Physics of the Earth and Planetary Interiors, 111:

21–34 .

Bullard, E.C., Freedman, C., Gellman, H., and Nixon, J., 1950. The

westward drift of the Earth’s magnetic field. Philosophical Trans-

actions of the Royal Society of London, 243:67–92.

Busse, F.H., 1976. Generation of planetary magnetism by convection.

Physics of the Earth and Planetary Interiors, 12: 350–358.

Chandrasekhar, S., 1961. Hydrodynamic and Hydromagnetic Stability.

Oxford: Oxford University Press.

Davidson, P.A., 2001. An Introduction to Magnetohydrodynamics.

Cambridge: Cambridge University Press.

El Sawi, M., and Eltayeb, I.A., 1981. Wave action and critical surfaces

for hydromagnetic-inertial-gravity waves. Quarterly Journal of

Mechanics and Applied Mathematics, 34: 187–202.

Eltayeb, I.A., 1972. Hydromagnetic convection in a rapidly rotating

fluid layer. Proceedings of the Royal Society of London Series A,

326: 229–254.

Eltayeb, I.A., 1981. Propagation and stability of wave motions in rotat-

ing magnetic systems. Physics of the Earth and Planetary Inter-

iors, 24: 259–271.

Eltayeb, I.A., and Kumar S., 1977. Hydromagnetic convective instabil-

ity of a rotating self-gravitating fluid sphere containing a uniform

distribution of heat sources. Proceedings of the Royal Society of

London Series A, 353: 145–162.

Ewen, S.A., and Soward, A.M., 1994. Phase mixed rotating magneto-

convection and Taylor’s condition. I. Amplitude equations. Geo-

physical and Astrophysical Fluid Dynamics, 77: 209–230.

Fearn, D.R., 1979. Thermal and magnetic instabilities in a rapidly

rotating sphere. Geophysical and Astrophysical Fluid Dynamics,

14: 102–126.

Fearn, D.R., and Proctor M.R.E., 1983. Hydromagnetic waves in a

differentially rotating sphere. Journal of Fluid Mechanics, 128:

1–20.

Finlay, C.C., and Jackson A., 2003. Equatorially dominated magnetic

field change at the surface of Earth’s core. Science, 300:2084–2086.

Hide, R., 1966. Free hydromagnetic oscillations of the Earth’s core and

the theory of geomagnetic secular variation. Philosophical Transac-

tions of the Royal Society of London Series A, 259:615–647.

Hide R., and Stewartson K., 1972. Hydromagnetic oscillations in the

Earth’s core. Reviews of Geophysics and Space Physics, 10:

579–598.

Jackson, A., Jonkers, A.R.T., and Walker, M.R., 2000. Four centuries

of geomagnetic secular variation from historical records. Philoso-

phical Transaction of the Royal Society of London, 358: 957–990.

Jones, C.A., Mussa A.I., and Worland S.J., 2003. Magnetoconvection

in a rapidly rotating sphere: the weak field case. Proceedings of the

Royal Society of London Series A, 459: 773–797.

Kerswell, R.R., 1994. Tidal excitation of hydromagnetic waves and their

damping in the Earth. Journal of Fluid Mechanics, 274:219–241.

Korte, M., and Constable, C., 2005. Continuous global geomagnetic

field models for the past 7 millennia II: CALS7K.1. Geochemistry,

Geophysics, Geosystems, 6(1): doi:10.1029/2004GC00801

Lehnert B., 1954. Magnetohydrodynamic waves under the action of

the Coriolis force. Astrophysical Journal, 119: 647–654.

Malkus, W.V.R., 1967. Hydromagnetic planetary waves. Journal of

Fluid Mechanics, 90: 641–668.

Moffatt H.K., 1978. Magnetic Field Generation in Electrically Con-

ducting Fluids. Cambridge: Cambridge University Press.

Proctor, M.R.E., 1994. Convection and magnetoconvection. In Proctor,

M.R.E., and Gilbert, A.D. (eds.), Lectures on Solar and Planetary

Dynamos. Cambridge: Cambridge University Press, 97–115.

Roberts, P.H., and Loper, D.E., 1979. On the diffusive instability of

some simple steady magnetohydrodynamic flows. Journal of Fluid

Mechanics, 90: 641–668.

Roberts, P.H., and Soward, A.M., 1972. Magnetohydrodynamics of

the Earth’s core. Annual Review of Fluid Mechanics, 4:117–153.

Roberts, P.H., and Stewartson, K., 1974. On finite amplitude convec-

tion in a rotating magnetic system. Philosophical Transactions of

the Royal Society of London, 277: 287–315.

Soward, A.M., 1979. Convection-driven dynamos. Physics of the

Earth and Planetary Interiors, 20: 281–301.

Walker, M.R., Barenghi, C.F., and Jones C.A., 1998. A note on

dynamo action at asymptotically small Ekman number. Geophysi-

cal and Astrophysical Fluid Dynamics, 88: 261–275.

Zhang, K., and Gubbins, D., 2002. Convection-driven hydromagnetic

waves in planetary fluid cores. Mathematical and Computer Mod-

elling, 36: 389–401.

Zhang, K., and Schubert, G., 2000. Magnetohydrodynamics in rapidly

rotating spherical systems. Annual Review of Fluid Mechanics, 32:

409–443.

Cross-references

Alfvén Waves

Alfvén, Hannes Olof Gösta

Core Convection

Core Motions

Inhomogeneous Boundary Conditions and the Dynamo

Magnetoconvection

Magnetohydrodynamics

Oscillations, Torsional

Proudman-Taylor Theorem

Thermal Wind

Time-Dependent Models of the Geomagnetic Field

Westward Drift

MAGNETOHYDRODYNAMICS

Introduction

Magnetohydrodynamics (MHD) is the study of the flow of electrically

conducting fluids in the presence of magnetic fields. It has significant

applications in technology and in the study of planets, stars, and

galaxies. Here the main focus will be on its role in explaining the ori-

gin and properties of the geomagnetic field.

The interaction between fluid flow and magnetic field defines the

subject of MHD and explains much of its fascination (and complex-

ity). The magnetic field B influences the fluid motion V through the

Lorentz force, J  B. The electric current density J is affected by the

fluid motion through the electromotive force (emf), V  B. The most

famous offspring of this marriage of hydrodynamics to electromagnet-

ism are the Alfvén waves, a phenomenon absent from the two subjects

separately (see Alfvén waves). In fact, many consider the discovery of

this wave by Hannes Alfvén in 1942 to mark the birth of MHD (see

Alfvén, Hannes). Initially MHD was often known as hydromagnetics,

but this term has largely fallen into disuse. Like MHD, it conveys

the unfortunate impression that the working fluid is water. In reality,

the electrical conductivity of water is so small that MHD effects are

essentially absent. Moreover, many fluids used in MHD experiments

are antipathetical to water. Even as fluid mechanics is now more

widely employed than hydrodynamics, the terms magnetofluid

mechanics or magnetofluid dynamics, which are already sometimes

employed, may ultimately displace MHD.

Since electric and magnetic fields are on an equal footing in electro-

magnetism (EM), it may seem strange that the acronym EMHD is not

preferred over MHD. In many systems, however, including the Earth’s

MAGNETOHYDRODYNAMICS 639

core, the application of EM theory in its full, unapproximated form

would add complexity without compensating enlightenment. It suffices

to apply the nonrelativistic version of EM theory that existed in the

19th century before Maxwell, by introducing displacement currents,

cast the theory into its present-day form. In this pre-Maxwell theory,

electric and magnetic fields are not on an equal footing; the magnetic

field is the master and the electric field the slave. Consequently MHD

is an appropriate acronym whereas EMHD is not. We exclude situa-

tions, such as those characteristic of electrohydrodynamics (EHD), in

which an electric field, E, is externally applied that is large compared

with the typical electric fields in MHD, which are created entirely by

the emf V  B.

The pre-Maxwell theory is described in the Section on Electro-

dynamics. It requires that the characteristic flow speed V is small com-

pared with the speed of light c, and that the characteristic timescale T

is large compared with L=c, where L is the characteristic length scale.

The theory to be described also demands that L is large compared with

the Debye length, which is the distance over which the number densi-

ties of electrons and ions can differ substantially from one another.

To simplify the discussion below, some verbal abbreviations will

usually be employed. In particular, velocity will mean fluid velocity,

density will stand for the mass density, field will mean magnetic field,

current will be short for electric current density, conductor will mean

conductor of electricity, potential will signify electric potential, and

core will refer to the Earth’s core. Script letters L, T , V, B, J, E,

etc., will indicate typical magnitudes of length, time, velocity, field,

current, electric field, etc. In the geophysical application, FOC means

fluid outer core; SIC, solid inner core; CMB, core-mantle boundary;

and ICB, inner core boundary.

Electrodynamics

Nonrelativistic electromagnetism

The pointwise form of the pre-Maxwell EM equations are, in SI units,

H  B ¼ J; (Eq. 1)

H  E ¼]

B; (Eq. 2)

H  B ¼ 0; (Eq. 3)

H  D ¼ #; (Eq. 4)

where D is the electric displacement, H is the magnetizing force and #

is the electric charge density; t is time and ]

¼ ]=]t. Equations (1) and

(2) are, respectively, Ampère’s law and Faraday’s law. The sources on

the right-hand sides of Eqs. (1) and (4) must satisfy charge conserva-

tion and, in pre-Maxwell theory, this requires

H  J ¼ 0; (Eq. 5)

which is consistent with Eq. (1). Equation (2) shows that, if Eq. (3)

holds for any t, it holds for all t.

Equations (1)–(5) are invariant under the Galilean transformation:

¼ x  Ut; (Eq. 6)

¼ t; (Eq. 7)

where x is the position vector and U is constant. The fields and sources

transform as

¼ B; (Eq. 8)

¼ E þ U  B; (Eq. 9)

¼ H; (Eq. 10)

¼ D þ U  H=c

; (Eq. 11)

¼ J; (Eq. 12)

¼ # þ H ðU  HÞ=c

: (Eq. 13)

According to (6) and (7), it follows that ]

¼ ]

þ U  H,fromwhich

it is readily verified that the primed variables also obey Eqs. (1)–(5).

The presence of the terms involving 1/c

in Eqs. (11) and (13) may

seem anomalous in a theory based on c L=T . However, since

H=D  c

B=E (see the Section on Constitutive relations), it follows

that all terms in Eq. (11) are of the same order, as are those in Eq. (13).

Equation (13) has the curious consequence that the free charge density

is frame-dependent.

We shall be interested in systems in which, on some surface S, the

properties of the medium change abruptly. We exclude cases in which

S separates the same material in different physical states and through

which the material passes, changing its state as it does so, as for a shock

discontinuity. The same integral laws that led to Eqs. (1)–(5) imply that

n  H½½¼C; on S; (Eq. 14)

n ðE þ U  BÞ½½¼0; on S; (Eq. 15)

n  B½½¼0; on S; (Eq. 16)

n  D½½¼S; on S; (Eq. 17)

n  J½½¼H

 C; on S; (Eq. 18)

where C and S are the surface current and the surface charge density

on S; H

is the two-dimensional surface divergence on S;

Q½½¼Q

 Q

is the difference in the limiting values of any quantity

Q at a point P of S from sides 1 and 2; the unit vector n to S is directed

out of side 2 and into side 1; U is now the velocity of P although only

the component of U along n is actively involved. The Galilean trans-

formation, when supplemented by

¼ S þ n  U  H½½=c

; (Eq. 19)

preserves Eqs. (14)–(18). Equations (13) and (19) may also be written as

¼ #  U  J=c

; (Eq. 20)

¼ S  U  C=c

: (Eq. 21)

Constitutive relations

The pre-Maxwell equations must be supplemented by relations that

define the physical nature of the medium in which they are applied.

We shall suppose that the medium is isotropic and homogeneous so

that, at a point P within it and in a reference frame moving with the

velocity U ¼ Vðx

Þ of P,

¼ B

=m; (Eq. 22)

640 MAGNETOHYDRODYNAMICS

¼ EE

; (Eq. 23)

¼ sE

; (Eq. 24)

where the proportionality variables are the permeability m, the per-

mittivity E, and the electrical conductivity s. Except in the crust, the

temperature within the Earth everywhere exceeds the Curie point, at

which permanent magnetism ceases to exist. We therefore assume that

m is the permeability of free space m

; the permittivity of free space is

and c

¼ 1=m

. When translated back to the laboratory frame,

(22)–(24) are, according to Eqs. (8), (10), and (12),

H ¼ B=m

; (Eq. 25)

D ¼ EE þðE  E

ÞV  B; (Eq. 26)

J ¼ sðE þ V  BÞ: (Eq. 27)

Wherever H occurs, we shall now use Eq. (25) to remove it, in favor

of B.

Equation (27) is the generalization of Ohm’s law to a moving con-

ductor, and is centrally important. It may be written equivalently as

E ¼V  B þ H  B; (Eq. 28)

where  ¼ 1=sm

is the magnetic diffusivity. This form provides a con-

venient way of removing E in favor of B; as mentioned in the Section

Introduction, E plays a subsidiary role in MHD. Nevertheless, it is

worth observing that, by Eqs. (3) –(5), (26), and (28),

# ¼E

H ðV  BÞ: (Eq. 29)

Unlike the case of a stationary conductor for which an initial #

flows to the boundaries in a time of order =c

(i.e., instantaneously

according to pre-Maxwell theory), the free charge density in a moving

conductor is generally nonzero, and takes the value (29).

EM energy conservation, ohmic dissipation,

Lorentz force

It follows from Eqs. (1) and (2) that

þ H  I

¼E  J; (Eq. 30)

where u

is the EM energy per unit volume and I

is the EM energy

flux (often called “the Poynting flux”):

¼ B

=2m

; (Eq. 31)

¼ E  B=m

: (Eq. 32)

When integrated over a small volume v surrounding a point P in the

medium, Eq. (30) states that the rate of increase of magnetic energy in

v is diminished by the outward flux of magnetic energy across its sur-

face s and by the rate at which the EM field transfers its energy to the

material contents of v, as determined from Eq. (28) as

 E  J ¼V  L  Q

; (Eq. 33)

where

L ¼ J  B; (Eq. 34)

¼ J

=s  0: (Eq. 35)

Here L, the Lorentz force, is the force per unit volume exerted by the

EM field on the medium, so that the net force and torque (about the

origin of x) on the contents of a volume v are

f ¼

Ldv ¼

J  Bdv; (Eq. 36)

G ¼

x  Ldv ¼

x ðJ  BÞdv: (Eq. 37)

The work done by the Lorentz force diminishes u

at the rate V  L.

When negative, this represents a transfer of kinetic energy to EM

energy. The second term on the right-hand side of Eq. (33), which is

necessarily nonnegative, gives the rate at which the EM field loses

energy through ohmic heating, also called Joule losses.

By using Eqs. (1), (3), and (34) it is possible, and often useful, to

replace the Lorentz force by an equivalent EM stress tensor:

¼r

; (Eq. 38)



: (Eq. 39)

Through Eq. (38), f and G may be replaced by surface integrals:

; (Eq. 40)

ijk

; (Eq. 41)

where, to obtain Eq. (41) the symmetry of p

has been invoked. Alter-

nate forms of Eqs. (40) and (41) are

f ¼

BðB  dsÞ





; (Eq. 42)

G ¼

x  B

ðB  dsÞ

x  ds



: (Eq. 43)

The first term on the right-hand side of Eq. (42) represents a tension

in the field lines; the second term contributes an isotropic magnetic

pressure, P

¼ B

=2m

, which is about 4 atm for a field strength of

1 T. These interpretations will be useful in the Section on the perfect

conductor below.

It is worth emphasizing that the magnetic field alone contributes

to the EM force on the conductor, to the EM stresses, and to the

EM energy. According to pre-Maxwell theory, the corresponding con-

tributions made by the electric field are smaller by a factor of order

ðV=cÞ

The induction equation; the magnetic Reynolds number

On eliminating E between Eqs. (2) and (28), it is found that B obeys

the induction equation,

]

B ¼ H ðV  BÞH ðH  BÞ: (Eq. 44)

This equation is sometimes called “the dynamo equation.” This is a

misnomer, since Eq. (44) is applicable in many situations totally unre-

lated to dynamo theory.

When  is constant (the usual assumption), Eq. (3) shows that

Eq. (44) can be written as

MAGNETOHYDRODYNAMICS 641

]

B ¼ H ðV  BÞþr

B: (Eq. 45)

This clearly exposes the evolution of B as a competition between EM

induction (through H ðV  BÞ) and ohmic diffusion (through

r

B), and it is convenient to introduce a dimensionless measure of

the relative importance of these effects:

¼VL= ¼ m

sVL: (Eq. 46)

In analogy with the familiar (kinetic) Reynolds number R

¼VL=n,

used in fluid mechanics to quantify the effects of viscosity, R

called the magnetic Reynolds number. (Here n is kinematic viscosity.)

An illuminating way of writing Eq. (45) is

B ¼ B  HV  B H  V þ r

B; (Eq. 47)

where d

¼ ]

þ V  H is the motional derivative, the derivative follow-

ing the fluid motion. This shows that, unless there is velocity shear

ðHV 6¼ 0Þ, the magnetic field will simply be advected by the motion

B) while being continually diffused by electrical resistance (through

r

B).

MHD processes in rotating bodies such as the core are usually most

easily studied using a reference frame that rotates with the body (see

the Section on Classical and Coriolis MHD). Even though E is then

different from the electric field in the inertial frame, the induction

equation is unchanged, provided ]

, d

, and V are defined relative to

the rotating frame.

Solutions to the induction equation are subject to the boundary condi-

tions (14)–(18). The first question to ask concerns the role of the surface

current C. From a physical standpoint, it is clear that, when  6¼ 0, an

infinitely thin concentration of current, even if it could be set up initially,

would be instantly diffused into a layer of large, but finite, J. This shows

that C ¼ 0 when  6¼ 0. Nevertheless, when R

 1, it is found that,

where material properties of the medium change abruptly, a thin

“boundary layer ” may arise, which, because J is so large, carries a finite

total current C. When focusing on phenomena on scales L large com-

pared with the thickness, d

, of the boundary layer, it may be conveni-

ent (even though  6¼ 0) to pretend that the boundary layer is infinitely

thin, i.e., is a surface current C (see Core, boundary layers).

A good example is provided by a rotating solid sphere of radius a across

which a uniform field, B

, is applied; the sphere rotates about an axis per-

pendicular to B

with angular velocity V (see also Dynamo, Herzenberg).

The appropriate magnetic Reynolds number is R

¼ Oa

=.Toanobser-

ver on the surface S of the sphere and rotating with it, the applied field will

seem to be oscillatory and, if R

 1, it will therefore penetrate only a

short distance, of order d

¼ R

1=2

a ¼ð=OÞ

1=2

, into the sphere. This

phenomenon is well known in the EM of solid conductors and is called

the “skin effect,” because the induced currentsare confined to a thin “skin”

on S. In the limit R

!1, the skin becomes infinitely thin, i.e., a surface

current C. This creates a dipolar magnetic field, b that completely

excludes B

from the interior of the sphere: n ðb þ B

Þ¼0on

S; Swirling motions in a fluid conductor can similarly expel flux

from within them.

For the remainder of this subsection, we suppose that R

¼ Oð1Þ and

C ¼ 0. Then, of Eqs. (14)–(18), only Eqs. (14)–(16) are significant:

½½B ¼ 0; on S; (Eq. 48)

½½n  E ¼ 0; on S: (Eq. 49)

By Eq. (28), condition (49) can also be written as

½½n ðV B H BÞ¼0, hence removing all reference to E when

solving Eq. (44) subject to Eqs. (48) and (49). This again highlights the

unimportance of E relative to B. If there is any interest in finding E, #,

and S, these can be determined after Eq. (44) has been solved, by apply-

ing Eqs. (28), (29), and (17).

Condition (18) is superfluous since, according to Eq. (1), it is satis-

fied when ½½n  B ¼ 0 is. Similarly, when Eq. (49) is obeyed, so is

½½n  B ¼ 0, by Eq. (2). Thus, only four of the five scalar conditions

(48) and (49) are independent. According to Eqs. (3) and (48),

½½n  Hðn:BÞ ¼ 0, but, because ½½ is generally nonzero, ½½n  J 6¼ 0,

so that

½½n:Hðn  BÞ 6¼ 0. Conditions (48) and (49) apply at the ICB

but usually the SIC is modeled as a solid of the same conductivity

as the fluid core ð½½ ¼ 0Þ, and moving with it at the ICB

ð½½V ¼ 0Þ. Then , by Ohm’s law ½½J  ¼ 0 and ½½HB ¼ 0.

Geophysically, a more significant application of Eqs. (48) and (49)

is when S is the CMB. Because the mantle is a relatively poor con-

ductor compared with the core, it is often assumed that the entire

region

V above the CMB is electrically insulating. Then, distinguish-

ing variables in

V by a circumflex and setting

J  0 in Eq. (1), we

have

H 

B ¼ 0; (Eq. 50)

H 

B ¼ 0: (Eq. 51)

(This also ignores all permanent magnetism in the crust.) Equations

(50) and (51) then show that

B is a potential field:

B ¼H

F; (Eq. 52)

where

F ¼ 0 : (Eq. 53)

This is the basis for the Gauss representation of the observed geo-

magnetic field. The general solution of Eq. (53) is a linear combination

of spherical harmonics, r

ðy; fÞ and r

n1

ðy; fÞ, the sources of

which are respectively outside the sphere of radius r and within it

(see Harmonics, spherical). Here ð r; y; fÞ are spherical coordinates,

with origin at the geocenter O and y ¼ 0 as north polar axis; the func-

tion S

ðy; fÞ is a surface harmonic, ðg

cos mf þ h

sin mfÞP

ðyÞ,

where P

ðyÞ is the Legendre function. For the main geomagnetic field,

the r

ðy; fÞ terms are found to be negligibly small at the Earth’s sur-

face and, when we assume that the mantle contains no sources of field,

this is also true at the core surface, r ¼ R

. The representation of

into a sum of r

n1

ðy; fÞ terms then holds throughout r  R

, and

(since magnetic monopoles do not exist), it is dominated at large r

by the first interior harmonic, r

2

ðy; fÞ, which corresponds to a

magnetic dipole. This leads to the important condition,

F ¼ Oðr

2

Þ; as r !1; (Eq. 54)

which expresses, in a succinct mathematical way, the fact that the

source of the main geomagnetic field lies entirely beneath the core

surface.

Conditions (48) and (49) hold on the CMB, but Eq. (49) does not

restrict solutions of Eq. (44). To see this, let us represent B and E in

a well-known way:

B ¼ H  A; (Eq. 55)

E ¼]

A  HC: (Eq. 56)

The Coulomb gauge is convenient in pre-Maxwell theory, so that

H  A ¼ 0; (Eq. 57)

C ¼#=E; (Eq. 58)

642 MAGNETOHYDRODYNAMICS

the second of which follows from Eqs. (4) and (23). Continuity of nB

and nE imply that ½½nA ¼ 0 and ½½C ¼ 0onS. Free charge may be

exist in

V, but it is reasonable to suppose that

#, and therefore

C also,

vanish as r !1. The Poisson equation (58) then determines

C. The

resulting ½½nrC is generally nonzero, and defines S on S (see Eq. (17)).

In short, Eq. (49) does no more than determine

E in

V and S on S;it

places no restriction on B. The essential difference between Eqs. (48)

and (49) is that surface layers of “magnetic charge,” analogous to sur-

face layers of electric charge, do not exist. This means that, while a

potential field

F can always be found that satisfies Eq. (54) together

with either ½½nB ¼ 0or½½nB ¼ 0, to demand that it satisfies both

these conditions places a restriction on B on S. This restriction

expresses the fact that all sources of B are currents flowing beneath

S. It is sometimes called “the dynamo condition.”

The kinematic dynamo

A self-excited dynamo is a device that maintains the magnetic field

indefinitely. Here “indefinitely” means that B 6! 0ast !1; “main-

tains” means that the only sources of B are currents flowing in the

conductor itself, i.e., there are no external current-carrying coils even

at infinity. The magnetic field is a by-product of the current flow

(see Eq. (1)), and in a self-excited dynamo, the motion creates from that

field the electromotive force that produces the required current flow.

There is no conflict with energy conservation. As seen in the Section

on EM energy conservation, ohmic dissipation, Lorentz force, the field

creates a Lorentz force and this in general opposes the motion and

attempts to bring the fluid to rest, an example of Lenz’s law. Some

agency has to maintain the motion, and provide the energy necessary

to make good the ohmic losses Q

. The self-excited dynamo is, in prin-

ciple, no different from generators of electricity in a power station.

Theorists distinguish two types of self-excited dynamo: the kine-

matic dynamo and the MHD dynamo. In a kinematic dynamo, the flow

V maintaining B is specified; in an MHD dynamo the energy sources

driving the flow are specified and B and V are determined simul-

taneously by solving the full MHD equations. These equations are

nonlinear and therefore much harder to solve than the induction equa-

tion, which is linear in B and is all that is needed (together with the

matching to a source-free external field

B) in studying the kinematic

dynamo. Not surprisingly, much is now known about kinematic

dynamos, and many solutions exist (see Dynamos, kinematic). In some

kinematic models, the conductor fills all space (see Dynamo, Herzenber g

and Dynamo, Ponomarenko). Because of applications of the dynamo

theory to the Earth and other heavenly bodies, it is more usual to

assume that the conductor occupies a simple, simply-connected body,

V, such as a sphere, the exterior

V of which is electrically insulating.

(See the Section on The induction equation; the magnetic Reynolds

number and see Dynamo, Backus; Dynamo, Braginsky; Dynamo,

Bullard-Gellman; and Dynamo, Gailitis. See also Dynamos, fast and

Dynamos, periodic.)

Maintenance of B obviously implies maintenance of u

. By assump-

tion, external sources do not bring magnetic energy into a system from

the outside so that, by Eqs. (30)–(33), the integral of VL over V must

be negative to offset the ohmic losses Q

, which is nonnegative at all

points in V. A necessary condition for dynamo action is therefore that

V is “sufficiently large,” i.e., R

is “big enough” (see Antidynamo and

bounding theorems). For convenience, we shall later say that R

0100

in a functioning dynamo, but it has to be clearly understood that a con-

dition such as that is far from sufficient to ensure dynamo action.

There are a number of antidynamo theorems that define circumstances

in which a dynamo will not work, no matter how large R

is (see Anti-

dynamo and bounding theorems). The most significant of these is a

result due to Cowling (1933) (see Cowling’s theorem). This states that

An axisymmetric magnetic field cannot be maintained by dynamo

action.

In what follows, axisymmetric quantities will be distinguished by an

overbar. More generally,

Qðr; yÞ will be the f—average of a scalar

quantity Qðr; y; fÞ; the remaining asymmetric part, Q

,ofQ will be

denoted by a prime: Q

¼ Q  Q. An axisymmetric field consists of a

zonal magnetic field,

, in the direction of increasing f and a

meridional field,

, that has only r and y components B

and

. The essence of Cowling’s theorem is that, although motions

can induce

from B

(see Section on the perfect conductor),

they cannot do the reverse; asymmetric field and flow are required to

produce an emf ð

 B

that creates the current, J

, necessary to

maintain

. This means that “dynamo fields are necessarily three-

dimensional,” i.e., their components must depend on r, y, and f. (Axi-

symmetric V are not, however, excluded by the theorem; e.g., see

Dynamo, Ponomarenko.)

Despite the antidynamo theorems, self-excited kinematic models

have been constructed and have been modeled in the laboratory

(see Dynamos, experimental). These successes and earlier work going

back to Parker (1955) have highlighted the importance of symmetry-

breaking; dynamos flourish if the motions lack mirror-symmetry (see

Geodynamo, symmetry properties). A flow is mirror-symmetric if a

mirror (z ¼ 0, say) exists such that

ðx; y; zÞ¼V

ðx; y; zÞ; V

ðx; y; zÞ¼V

ðx; y; zÞ;

ðx; y; zÞ¼V

ðx; y; zÞ: (Eq: 59)

The simplest manifestations of such symmetry-breaking are helical

motions. Helicity is defined as V  v, where v ¼ H  V is the vorti-

city of the flow. It is a measure of how mirror-symmetric the flow

is; like a common carpenter’s screw, a helical flow does not look the

same when viewed in a mirror. Helicity is created naturally in convect-

ing systems that are rotating; the rising and falling motions created by

buoyancy acquire vertical vorticity through the action of the Coriolis

force. The word helicity is a term in general use to describe any quan-

tity that is the scalar product of a vector with its curl, such as the

magnetic helicity, A  Bð¼ A  HAÞ, and the current helicity,

BJð¼ BHB=m

Þ. Helical flows tend to produce helical fields, as

measured by the magnetic and current helicities.

Although examples exist of kinematic dynamos that function even

though the motions are nonhelical, there is little doubt that helical

dynamos are more efficient, i.e., they function at smaller values of

. The simplest manifestation of this is the alpha-effect, in which

helical motions produce a mean emf

B

that is proportional to B

and is usually written as a

B. This includes an emf aB

in the f-direc-

tion that drives the f-component of

J that creates the axisymmetric

meridional part,

,ofB needed to defeat Cowling’s theorem

(see above). This simple fact largely explains the popularity of

mean field dynamos, where only the axisymmetric part of B is sought,

induction by the asymmetric parts being parameterized by an ansatz,

such as the simple choice

B

¼ aB just made (see Dynamos,

mean field).

The perfect conductor

A perfect conductor is one that has infinite electrical conductivity

ð ¼ 0Þ. Since J must be finite even though s ¼1, Ohm’s law (27)

implies that

E ¼VB: (Eq. 60)

The induction equation becomes

]

B ¼ HðVBÞ when  ¼ 0: (Eq. 61)

In a perfect conductor, the magnetic Reynolds number, R

, is infinite;

see Eq. (46). Although R

 1 in many applications of MHD (includ-

ing some considered here), R

¼1is an idealization that is never

achieved. It is however an abstraction that is often useful. This is a

consequence of Eq. (61) from which it follows that (see Alfvén’s the-

orem and the frozen flux approximation).

MAGNETOHYDRODYNAMICS 643

Magnetic flux tubes move with a perfect conductor as though

“frozen” to it.

Frozen flux provides a useful way of picturing MHD processes when

is large, one that employs some of the concepts of stress and energy

of the Section on EM energy conservation, ohmic dissipation,

Lorentz force. Consider the way in which fluid motions can exchange

energy with the field. Imagine a straight flux tube, initially of cross-

sectional area A

, lying in a compressible fluid. Suppose a motion com-

presses the tube uniformly, so that, while remaining straight, its cross-

sectional area is reduced to A ð< A

Þ. The density of the fluid it contains

increases from its initial value of r

to r ¼ r

ðA

=AÞ. If the compres-

sion is performed fast enough, heat conduction is negligible. In such

an adiabatic process, the internal energy of the tube increases, so that

its temperature rises. According to Alfvén’s theorem, the flux of the

magnetic field in the tube cannot change, so that the field B

initially

within the tube increases in strength to B ¼ B

=A, i.e., by the same

factor as the density; thus B=r remains at its initial value, B

. The

magnetic energy per unit length contained in the tube increases, how-

ever, from A

ðB

=2m

Þ to AðB

=2m

Þ¼½A

ðB

=2m

ÞðA

=AÞ. In short,

the kinetic energy of the compressing motion has been transformed into

internal energy and magnetic energy. The reverse happens if A > A

; the

flux trapped in an intense tube tends to expand into surroundings where

the field is weaker. For these reasons, sound traveling across a field

moves faster than it would in the absence of the field; the magnetic pres-

sure created by the field intensifies the restoring force in the compres-

sions and rarefactions of the wave.

The transformation of kinetic energy into magnetic energy also

occurs in an incompressible fluid when motions stretch field lines

against their tension. The process may be likened to the storing of elas-

tic energy in a stretched rubber band or to the energy transmitted to a

violin string by plucking it. If the flux tube of cross-sectional area A

containing field B

is lengthened from L

to L, its cross-section

will decrease in the same proportion ðA ¼ A

=LÞ and the field

within it will increase by the same factor ðB ¼ B

L=L

Þ. The magnetic

energy it contains, which is proportional to B

, is enhanced by a factor

of ðL=L

from ðB

=2m

ÞL

to ðB

=2m

ÞLA ¼ðB

=2m

ÞL

½ðB

=2m

ÞL

ðL=L

.IfL ¼ L

þ d where d  L

, the increase in

magnetic energy is ðB

ÞA

d. This is the work done by the applied

force in stretching the tube by d in opposition to the magnetic tension

ðB

ÞA

of the field lines.

It was mentioned in the Section on the induction equation; the mag-

netic Reynolds number that fluid motions can create

from B

Alfvén’s theorem provides a picture of the process: a zonal shearing

motion

drags the lines of force of B

out of their meridional

planes, i.e., it gives them a

component. Dating from a time when

the zonal shear,

=rsiny, was frequently denoted by o, this is often

called the omega effect. Taking Alfvén’s theorem literally,

will

continue to wind the field lines around the symmetry axis for as long

as the motion is maintained, and

and u

will increase monotoni-

cally. The magnetic stresses grow as the field lines become increasingly

stretched in the f-direction until at last the agency that creates

can

no longer maintain it.

Alfvén’s theorem leads to a new phenomenon, the Alfvén wave.

Consider again the straight flux tube, of cross-sectional area A in an

incompressible fluid, and imagine that a transverse displacement bends

the tube, carrying its contents with it, in obedience to the theorem. The

tension t ¼ AB

of the tube acts, as in a stretched string, to shorten

the tube. A wave results, which moves in each direction along the tube

with speed V

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðt=MÞ

, where M ¼ rA in the mass per unit length

of the string. The wave velocity is therefore

¼ B=ðm

rÞ

1=2

; (Eq. 62)

which is usually called the Alfvén velocity. It is the speed with which

energy can be transmitted along the field lines. On taking

B¼0:01 T and r ¼ 10

kg m

3

as typical of the core, it is found that

 0:1ms

1

. The MHD or Alfvénic timescale,

¼L=V

; (Eq. 63)

is often significant. It provides an estimate of how quickly an MHD

system responds to changes in its state. Alfvén waves are the simplest

example of a wider class of waves; see the Section on the CMHD for

ideal fluids and Magnetohydrodynamic waves.

It was seen in the Section on the induction equation; the magnetic

Reynolds number that C may be nonzero at a surface S of discontinu-

ity when  ¼ 0 on one side of S. This surface current is subjected to a

Lorentz force that is computed best through the EM stress tensor (39).

The discontinuity in magnetic stress is then

½½p

 ¼

ðn  BÞðC  nÞ½½P

n: (Eq. 64)

This can be written, in analogy with J  B,asC 

ðB

þ B

Þ.

Other stresses must act to compensate for this discontinuity. For exam-

ple, if n  B ¼ 0, the discontinuity in P

¼ B

=2m

can be compen-

sated by a discontinuity in the kinetic pressure P that makes the total

pressure, P

total

¼ P þ P

, continuous. Even if a discontinuity in P

total

could be set up initially, it would immediately be radiated away from

S sonically. If n  B 6¼ 0, the situation is more complicated but it

is helpful to recall (See the Section on the induction equation; the mag-

netic Reynolds number) that the surface current is an idealization for

!1of a thin boundary layer in which other processes may be

significant. For example, the surface force ðn  BÞðC  nÞ=m

Eq. (64) represents the limit of a volumetric force that would create

a large velocity shear in the boundary layer; associated with this is a

large viscous stress that may be able to balance the magnetic stress,

as in the Hartmann layer (See the Section on the Classical MHD). In

the absence of such effects, one must assume that C ¼ 0 when

n  B 6¼ 0. Even if a surface current could be set up initially, it would

immediately be Alfvénically radiated away from S.

The imperf ect conductor, reconnection

Some caution has to be exercised in applying Alfvén’s theorem.

According to the theorem, the topology of field lines cannot change.

Fluid lying on a field line always remains on that field line; reconnec-

tion of field lines is impossible. This makes the dynamo problem

meaningless; the magnetic flux trapped in the conductor is never lost,

and one cannot even find out how the conductor acquired that flux ori-

ginally. Magnetic field is gained, retained, or lost only by its diffusion

relative to the conductor, and diffusion happens only when s and R

are finite. Nevertheless, Alfvén’s theorem is useful in picturing what

happens when R

is large. As the conductor moves, it loses flux on

the EM diffusion timescale, t



, but this may be replenished by a shearing

processes (such as those considered above) on the advective timescale

; here



¼L

=; (Eq. 65)

¼L=V: (Eq. 66)

For a dynamo to be successful, renewal of flux must balance or

exceed its destruction, i.e., t

must be shorter than t



, implying that

¼ t



0Oð1Þ. The westward drift velocity on the CMB

of recognizable features of the geomagnetic field is of order

3  10

4

1

. It is likely however that part of this motion is due

to diffusion of the features relative to the conductor. A magnetic feature

of scale L can diffuse relative to the conductor at a drift speed c

order =L. We shall therefore assume that the actual fluid velocity is less

644 MAGNETOHYDRODYNAMICS

than 3  10

4

1

and estimate that V¼10

4

1

. Taking

L2  10

m and  ¼ 2m

1

, this gives R

 100.

Because of the small scale of laboratory apparatus, it is hard to

achieve O(1) values of R

. For the same reason, it is hard to demon-

strate dynamo action using liquid metals (but see Dynamos, experi-

mental). The frozen flux picture is of limited usefulness in

describing MHD experiments with liquid metals. When R

 1, EM

diffusion is rapid ðt



 t

Þ and, in the limit, instantaneous. The

left-hand side of Eq. (44) is then negligible compared with

H ðH  BÞ, and, on uncurling this equation, we obtain the limiting

form that is the antithesis of Eq. (60):

J ¼ sðHC þ V  BÞ: (Eq. 67)

This is equivalent to the statement that E is a potential field

ðE ¼HCÞ, the potential of which can be obtained by solving the

Poisson equation that follows from Eq. (67):

C ¼ H ðV  BÞ: (Eq. 68)

The first term on the right-hand side of Eq. (67) is nonlocal, i.e., it

depends on the form of V and B everywhere. The second term creates

a current sVB and a local Lorentz force sðVBÞB, from the pre-

vailing V and B. The latter may be written as  V

, where

¼ V ðVBÞB=B

is the part of V that is perpendicular to B,

and t

is the magnetic damping time:

¼ r=sB

¼ =V

: (Eq. 69)

This shows that, when R

 1, the primary effect of a field is to

damp-out motions across magnetic field lines, rather like an anisotro-

pic friction (Davidson, 2001).

Because of the small scale of laboratory apparatus, it is also hard to

demonstrate Alfvén waves in the laboratory. After the wave has traveled

a distance V



, the comoving induced currents have essentially dif-

fused away. The condition that a wave can cross the system before disap-

pearing is V



0L or Lu01, where Lu is the Lundquist number:

Lu ¼V

L= ¼

ðt



Þ: (Eq. 70)

If B¼0:1 T is the strength of a field applied across a liquid sodium

system of scale L¼0:1 m, we have V

 3ms

1

,   1m

1

 0:1s,t



 0:01 s, and Lu  0:3.

Some effects of turbulence

Many fluid systems occurring in nature are turbulent. The fluid flow

within them exists on length scales that range from L

macro

, comparable

with the dimensions L of the system, to L

micro

L

macro

, where by

macro is meant large scales and by micro small scales (though still

much larger than intermolecular distances). The corresponding mag-

netic Reynolds numbers range from R

m;macro

¼V

macro

=0Oð1Þ

to R

m;micro

¼V

micro

=  R

m;macro

. In a violently turbulent envir-

onment such as the solar convection zone, even R

m;micro

01 so that

these scales of motion can generate a small-scale field by themselves.

From seeds planted by an epoch-making paper by Parker (1955), a

new subject grew called mean field electrodynamics in which the con-

cepts of mirror-symmetry and a-effect were central (see, for example,

Krause and Rädler, 1980). It was shown that the microscale field and

motion not only generate a macroscale field by the a-effect but also

destroy it by an enhanced turbulent diffusivity, 

, vastly greater than

the molecular (or radiative) value, . This was advanced as an explana-

tion of why the solar field reverses its polarity on a timescale,

;T

¼L

=

, of 11 years even though t



¼L

= is greater than the

age of the Sun. During the 22-year cycle, sunspots are seen as markers

for a large-scale field that drift equatorward relative to the fluid with a

velocity of order c

d;T

¼ 

=L.

If the Earth’s core were as turbulent as the Sun, the timescales of the

geomagnetic field would be similarly shortened. The paleomagnetic

evidence indicates however that polarity reversals are completed in a

time comparable with t



¼L

= which, taking L10

m and

 ¼ 2m

1

, is of order 10

years. This strongly suggests not only

that turbulence in the core is much less violent than in the convection

zone of the Sun (which is hardly surprising) but also that R

m,micro

the core is too small for EM induction by small eddies to affect the

large-scale field significantly. If this is the case, the concepts of mean

field electrodynamics are not applicable to the core, the turbulent

a-effect is negligibly small, and 

does not dominate . We shall

therefore ignore 

in what follow. According to these arguments,

the geodynamo operates on the macroscale, for which the concepts

of mirror-symmetry, helicity, and a-effect apply only in a global non-

local sense, as for the waves to be mentioned in the Section CMHD

for ideal fluids below.

The microscales are, nevertheless, significant in another way; they

considerably enhance the energy requirements Q

of the geodynamo.

The current densities associated with the macro- and microscales are

related to their respective field strengths, B

macro

and B

micro

by Eq. (1):

macro

B

macro

; J

micro

B

micro

(Eq. 71)

Although it may be true that B

micro

B

macro

, it is also true that

micro

L

macro

. It follows that J

micro

may be comparable with

macro

, and therefore its contribution to Q

¼ J

=s may be of a

similar size. As shown in the Section on The imperfect conductor,

reconnection, the microscale fields for which R

m;micro

 1 create a

Lorentz force, of order  rV

, and this acts like an anisotropic

friction. The energy expended working against this friction is dissi-

pated ohmically (see also Core turbulence).

Fluid dynamics

Energy sources

It is clear that an energy source is needed to maintain fluid flow in the

face of viscous friction; in addition, an MHD system must expend

further energy ohmically. In laboratory systems, the required energy

is frequently supplied by pumps that force fluid flow through pipes

or channels, and the magnetic field is usually generated externally. In

contrast, many naturally occurring fluid systems are forced into motion

by buoyancy forces and, because of their vast dimensions L, can easily

satisfy the condition R

0100 necessary for dynamo action at quite

modest flow speeds V. Moreover, these systems are often rotating,

and the convective motions may then lack the mirror-symmetry that

is detrimental to dynamo action; in other words, they possess helicity

(see the Section on The kinematic dynamo). Not surprisingly, there-

fore, they are often able to equip themselves with the magnetic field

that transforms them into MHD systems.

Buoyancy is not the only way of creating fluid flow; laboratory

motions are sometimes produced by moving the walls of the container;

and, in a similar way, flows in planetary cores can be forced at their

boundaries. For example, motions in the core are affected by the luni-

solar precession. This causes the Earth’s axis of rotation to describe a

cone of semiangle 23



about an axis perpendicular to the ecliptic in

a period of about 26 ka. The associated motion of the CMB affects

the fluid flow in the core and may even be the main mechanism

driving it (see Tilgner, 2005, and Precession and core dynamics). So

far, a definitive assessment of the geophysical importance of precession

is lacking.

Because MHD turbulence is poorly understood, it is hard to estimate

the total energy requirements of the motions and fields in the Earth ’s

core. Because the core is a liquid metal, its kinematic viscosity

nð 10

6

1

Þ is substantially less than its magnetic diffusivity

ð 2m

1

Þ, i.e., its magnetic Prandtl number,

MAGNETOHYDRODYNAMICS 645