Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials

Подождите немного. Документ загружается.

Ch_02.qxd 11/30/04 8:45 AM Page 112

3 Atomistic Computer Simulation

of Diffusion

Yuri Mishin

School of Computational Sciences

George Mason University, Fairfax, Virginia

3.1 Introduction

The past decades have seen a tremendous increase in the application

of computer modeling and simulation methods to diffusion processes in

materials. Along with continuum modeling aimed at describing diffu-

sion processes by differential equations, atomic-level modeling is playing

an increasingly important role as a means of gaining fundamental insights

into diffusion phenomena.

One of the reasons for the growing interest in the atomistic modeling

of diffusion is the recognition that experimental methods only deliver

effective diffusion coefficients, i.e., coefficients averaged over the diffu-

sion zone and over many atomic jumps contributing to the diffusion flux.

Recovering information relating to individual diffusion mechanisms, their

activation barriers, correlation factors, and other atomic-level characteris-

tics is extremely difficult, if not impossible. As a result, many experimen-

tal measurements produce useful reference numbers for handbooks and

immediate technological applications (which is very important too) but do

not add much to our basic understanding of diffusion processes. In the

long run, however, it is highly desirable to be able to predict diffusion

coefficients by calculation. This ability is critical for the ongoing effort to

reduce the dramatic costs associated with the development of new tech-

nologically advanced materials by the traditional empirical approach.

Atomistic modeling appears to offer the only viable way of gaining

insights into mechanisms of complex diffusion processes and thus creat-

ing a fundamental framework for predictive diffusion calculations.

A second reason for this growing interest is that drastically increased

computer speeds have enabled computer simulations that could only be

dreamed about just two decades ago. New methods have been developed

that provide a realistic description of atomic interactions in materials,

accelerate molecular dynamics (MD) and Monte Carlo simulations, and

allow more reliable calculations of transition rates. The new methods provide

Ch_03.qxd 11/29/04 6:08 PM Page 113

114 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

access to diffusion processes in larger and more complex systems and

allow us to observe diffusion over more extended periods of time. Some

of the recent atomistic calculations of diffusion coefficients show an

encouraging agreement with experimental data.

This chapter presents an overview of atomistic simulation methods cur-

rently available for diffusion modeling in materials, focusing on metals and

metallic systems. When examining each method or class of methods, some

background, leading literature references, and a brief overview of the most

recent developments are provided. Although various examples of applica-

tions are discussed along the way, two areas are emphasized where much

progress has recently been achieved due to computer simulations. The first

area is diffusion in ordered intermetallic compounds. The atomic order in

such compounds imposes strong selection rules on possible diffusion mech-

anisms by favoring mechanisms that either preserve the order or destroy it

only locally and temporarily. A glimpse of understanding of such mecha-

nisms is now emerging through computer simulations. The other area is dif-

fusion in grain boundaries, in which new collective mechanisms have been

discovered that involve both vacancies and interstitials as equal partners.

The common thread of these and other examples is the notion that atomistic

computer simulations offer a powerful tool for gaining deeper insights into

diffusion phenomena, and that this tool is applicable not only to simple sys-

tems but also to complex materials of technological importance.

3.2 Atomic Interaction Models

3.2.1 Embedded-Atom Method

The first step in any atomistic simulation is to establish a model that

describes atomic interactions. Because diffusion processes involve the

motion of atoms over considerable distances and require statistical aver-

aging, diffusion simulations inevitably deal with relatively large ensembles

of atoms. This explains why the overwhelming majority of such simula-

tions are based on classical interatomic potentials, also called force fields.

Interatomic potentials allow fast MD and Monte Carlo simulations to be

performed for systems containing up to millions of atoms. Early diffusion

simulations used pair potentials of the Morse or Lennard-Jones type.

Although useful insights were obtained, the agreement with experiment

was only qualitative at best. The problem with pair potentials is that they

do not capture the nature of atomic bonding even in simple metals, not to

mention transition metals or covalent solids. The invention of the embed-

ded-atom method (EAM)

[1, 2]

in the 1980s opened a new page in atomistic

simulations. Due to the incorporation, in an approximate manner, of

Ch_03.qxd 11/29/04 6:08 PM Page 114

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 115

many-body interactions between atoms, EAM potentials have enabled a

semi-quantitative and, in good cases, even quantitative description of

interatomic bonding in metallic systems.

In the EAM model, the total potential energy E

tot

of a collection of

atoms is given by the expression:

tot



i,j

) 



). (1)

Here, Φ

is the pair-interaction energy between atoms i and j at positions

→

and r

→

 r

→

 r

→

, respectively. F

is the embedding energy of atom i, and



is the host electron density at site i induced by all other atoms in the

system. The latter is given by the sum:





j≠i

), (2)

where r

(r) is the electron density function assigned to atom j. The second

term in the right-hand side of Eq. (1) represents many-body effects, which are

responsible for a significant part of bonding in metallic systems. The EAM

has an excellent record of describing basic properties of simple and noble

metals,

[3]

but is less accurate for transition metals. The latter reflects the

intrinsic limitation of the EAM, which is essentially a central-force model

and is, therefore, unable to capture the covalent component of bonding due

to d-electrons present in transition metals. The EAM has also been applied,

with reasonable success, to several intermetallic compounds.

[4–6]

The functional form of Eq. (1) was originally derived as a generaliza-

tion of the effective medium theory

[7]

or the second moment approxima-

tion to tight-binding theory.

[2, 8]

Later, however, Eq. (1) lost its close ties

with the original physical meaning and came to be used as a semi-empirical

expression with adjustable parameters. The potential functions Φ

(r),

(r), and F



) are typically parameterized with three to five fitting

parameters each and are fit to selected properties of the material. While

early EAM potentials were fit to experimental properties only, the current

trend is to incorporate into the fitting database both experimental and first-

principles data. The experimental properties traditionally include the lattice

constant, cohesive energy, elastic constants, thermal expansion factors,

and phonon frequencies, as well as the vacancy formation energy and the

stacking fault energy. The first-principles data usually come in the form of

energy-volume relations for the ground-state structure and a few hypo-

thetical structures of the material. Furthermore, first-principles energies

along uniform deformation paths between the structures were calculated on



Ch_03.qxd 11/29/04 6:08 PM Page 115

116 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

several occasions, although they were used primarily for testing rather

than fitting the potentials.

[5, 6, 9, 10]

An alternative way is to include a set of

interatomic forces drawn from snapshots of first-principles MD simula-

tions for the solid and liquid phases of the material (force matching

method).

[11]

The incorporation of first-principles data into the fitting data-

base improves the reliability of the potential due to the sampling of atomic

configurations away from those represented by experimental data.

[9–12]

For

a binary system A-B, the cross-interaction function Φ

(r) is optimized by

fitting to experimental andor first-principles data for the experimentally

observed andor hypothetical compounds, usually with several stoichio-

metric compositions to cover a broader region of configuration space.

3.2.2 Angular-Dependent Potentials

Baskes and co-workers

[13–16]

developed a non-central-force extension

of the EAM, called the modified embedded-atom method (MEAM). In the

MEAM, the electron density is treated as a tensor, and the host electron

density r



is expressed as a function of the respective tensor invariants. In

the simplest approximation, r



is given by the expansion:



)

 (r



(0)

)

 (r



(1)

)

 (r



(2)

)

 (r



(3)

)

, (3)

where



(0)

)





j≠i

(0)

)



, (4)



(1)

)





j≠i

(1)

)



, (5)



(2)

)



a,b



j≠i

(2)

)







j≠i

(2)

)



, (6)

(rr



(3)

)



a,b,g



j≠i

(3)

)



. (7)

Here a, b, and g  1,2,3 are summations over Cartesian coordinates of the

radius-vector r

→

. The terms r



(k)

(k  0,1,2,3) represent contributions



Ch_03.qxd 11/29/04 6:08 PM Page 116

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 117

corresponding to s, p, d, and f electronic orbitals, respectively. The regu-

lar EAM is recovered by including the electron density of s-orbitals only

and neglecting all other terms [compare Eq. (2)].

In comparison with the regular EAM, the MEAM introduces three

additional parametric functions, r

(1)

(r), r

(2)

(r), and r

(3)

(r), for each species,

which are fit to the same type of database as in the EAM. Furthermore,

while EAM potential functions are typically long-ranged and are smoothly

truncated on a sphere encompassing several coordination shells, the

MEAM uses short-range functions (1-2 coordination shells) but introduces

a many-body screening procedure described in detail by Baskes.

[15, 17]

Computationally, MEAM simulations are slower than EAM simulations,

but the MEAM is more suitable for transition metals and can even be

applied to covalent solids, such as Si and Ge.

[15]

MEAM potentials have

been constructed for many FCC, BCC, and HCP metals,

[15, 17, 18]

as well as

for several compounds, including Mo silicides

[19]

and TiAl.

[20]

Pasianot et al.

[21]

proposed a slightly different way of incorporating

angular-dependent interatomic forces into the EAM. In their so-called

embedded-defect method (EDM), the total energy is written as:

tot



i,j

) 



)  G

, (8)

where





j≠i

), (9)



a,b



j≠i

)







j≠i

)



. (10)

Equation (8) was originally derived from physical considerations different

from those underlying the MEAM. However, mathematically, Eqs. (8)

through (10) represent a particular case of Eqs. (1) through (7), in which

the terms r



(1)

and r



(3)

are neglected, F(r



) is approximated by a linear

expansion in terms of the small perturbation r



(2)

, and the latter is

expressed through the unperturbed electron density function r

(r). In com-

parison with the regular EAM, the EDM contains only one additional

adjustable parameter, G. Like the EAM, the EDM is based on cutoff func-

tions and does not involve any screening procedure. EDM potentials have

been constructed for HCP

[22]

and BCC transition metals.

[21, 23–25]

A number of specific, usually angular-dependent, interatomic poten-

tials have been constructed for silicon, carbon, and other semiconductor



Ch_03.qxd 11/29/04 6:08 PM Page 117

118 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

materials.

[26–29]

Likewise, accurate empirical and semi-empirical potentials

have been developed for many ionic systems.

[30, 31]

3.2.3 More Accurate Methods

An encouraging trend in recent years is the appearance of diffusion

studies using first-principles methods based on the density-functional

theory.

[32]

Such methods have been applied to calculate vacancy forma-

tion energies in a number of metals and intermetallic compounds.

[33–41]

While early first-principles calculations used relatively small supercells

with 16 to 32 atoms, the sizes of systems accessible by such methods

rapidly increase with computer power. For example, the Vienna Ab ini-

tio Simulation Package (VASP),

[42, 43]

in conjunction with ultra-soft

plane-wave pseudopotentials,

[44]

already gives access to systems con-

taining a few hundred atoms. Clearly, the role of first-principles methods

in diffusion will continue to grow rapidly in the years to come.

Presently, however, such methods are limited to molecular statics calcu-

lations of point defect formation energies and, in rare cases, of migration

energies. Meaningfully long MD or Monte Carlo simulations are not yet

feasible.

Another group of methods worth mentioning comprises semi-empirical

methods based on tight-binding theory, particularly bond-order potentials

(BOPs)

[8, 45–48]

and the tight-binding method developed at the U.S. Naval

Research Laboratory (NRL-TB).

[49–51]

Both methods contain adjustable

parameters that are optimized by fitting to experimental and first-principles

data (BOP), or to first-principles data only (NRL-TB). Besides properties

that depend on the total energy, the NRL-TB Hamiltonian is also fit to the

electronic band structure of the material.

[49–51]

In contrast to classical poten-

tials, these methods are based on quantum mechanics and explicitly

address the electronic structure of the material. An appealing feature of

these methods is their ability to handle both simple and transition metals,

intermetallic compounds, and semiconductors. Although BOP and NRL-

TB methods are almost two orders of magnitude slower than EAM calcu-

lations, they are much faster than first-principles methods. In a sense, they

serve to bridge the gap between semi-empirical and first-principles methods.

For example, it has been demonstrated that the NRL-TB method can read-

ily implement thousands of MD steps on a system containing about a thou-

sand atoms.

[52–54]

The computational efficiency of such methods invariably

improves as processors become faster and new parallel computer codes are

developed. Such methods can start playing a role in diffusion simulations

in the future.

Ch_03.qxd 11/29/04 6:08 PM Page 118

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 119

3.3 Molecular Statics

3.3.1 Simulation Block and Boundary Conditions

The most common procedure in atomistic simulations is the static

relaxation, i.e., minimization of the total energy of a system with respect

to atomic positions as well as other degrees of freedom available to it. The

system is represented in the computer by a finite set of atoms, called a

simulation block (or simulation cell), which is subject to suitable bound-

ary conditions.

[30, 31, 55–57]

To accelerate the relaxation of a large block, the

computer program generates and stores in the memory a list of appropri-

ately close neighbors of each atom. This makes the computation an effec-

tively linear-N process, N being the number of atoms in the block. If the

relaxation is accompanied by large atomic displacements, the neighbor

list should be promptly updated. The construction of a neighbor list for a

large block is a computationally expensive procedure by itself, but it can

be accelerated by applying the link-cell method and other tricks of the

trade that are well documented in the literature.

[56, 57]

If the boundary conditions are periodic in all directions, the block is

often called a supercell, the term borrowed from the area of first-principles

calculations. Often, the movable (free, or dynamic) atoms are embedded in

a mantel of fixed atoms, i.e. atoms frozen in their perfect-lattice positions

relative to one another (fixed-boundary condition). The thickness of the

mantel is made larger than the distance at which atoms can “see” each

other, so that the free surfaces separating the mantel from vacuum would

not affect the dynamic atoms. Different boundary conditions can be com-

bined with each other, i.e., be fixed in some directions and periodic in other

directions. For example, in typical grain boundary (GB) simulations, the

boundary conditions are periodic in directions parallel to the GB plane and

fixed in the direction normal to the GB plane. In this geometry, the fixed

atoms represent lattice regions far away from the GB (the grains).

The choice of boundary conditions for simulating lattice disloca-

tions is a more delicate matter because the elastic strain field around a

dislocation is long-ranged and boundary conditions may have a sub-

stantial effect on the dislocation core structure.

[55]

For an isolated dis-

location, simulations usually use a cylindric geometry with the dislocation

line aligned parallel to the cylinder axis (periodic direction). Prior to

beginning the relaxation, the fixed atoms in the cylindrical mantel are

displaced according to the elasticity theory solution for the elastic

strain field of a straight dislocation with the chosen Burgers vector.

Recently, Rao et al.

[58]

proposed a more accurate boundary condition, in

which the atomic displacements in the fixed region are determined in a

Ch_03.qxd 11/29/04 6:08 PM Page 119

120 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

self-consistent manner through the lattice Green function (flexible, or

Green-function boundary condition). Furthermore, it has been demon-

strated that this boundary condition makes it possible to reduce the size

of the free region (containing the dislocation core) to the extent that it

can be simulated by first-principles methods.

[59]

This boundary condi-

tion could be applied in future atomistic simulations of dislocation pipe

diffusion.

3.3.2 Point-Defect Formation Energy

Point defects also produce long-range elastic fields, and their com-

puted properties generally also depend on the boundary condition. As a

simple example, we will consider the calculation of the formation energy

of a single vacancy in a metal. This energy is determined as the total

energy of a relaxed simulation block containing a vacancy minus the

energy of the perfect lattice containing the same number of atoms. A part

of e

is associated with strong atomic distortions within the vacancy core,

but a significant part is stored in the elastic deformation field around the

vacancy. It can be shown that the elastic energy stored within a sphere of

radius R around a point defect converges to its value in an infinite system

as 1R

when R → ∞.

[60, 61]

Since simulations are performed in a finite-size

block, the elastic field is disturbed by the block boundaries, and the result-

ing e

value is either underestimated or overestimated, depending on the

boundary condition.

Two types of boundary conditions are typically used in point-defect

simulations. Under the constant-volume condition, the volume of the

block is fixed at its initial, perfect-lattice value, and only atomic positions

are allowed to vary during the energy minimization. Under the zero-pressure

condition, both the volume and atomic positions are relaxed simultane-

ously. It can be shown that the vacancy formation energy converges as

1N (N → ∞) to the same value, regardless of the boundary condition.

[61]

Furthermore, it turns out that the constant-volume condition always over-

estimates the true vacancy formation energy, whereas the zero-pressure

condition always underestimates it.

[61]

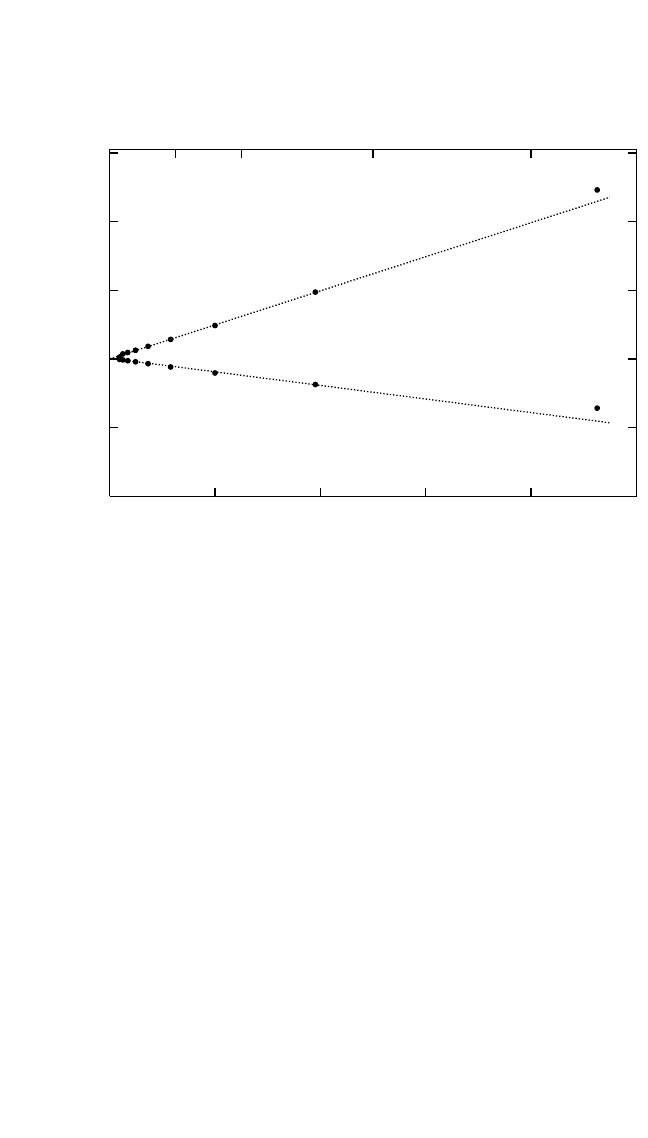
This fact is illustrated in Fig. 3.1

using EAM calculations of the vacancy formation energy in copper as an

example. The zero-pressure branch of the plot has a slightly smaller slope,

which agrees well with the elasticity theory analysis within a simple

spherical model.

[61]

However, even though the smaller slope means a

faster convergence, the difference in the slopes of the two branches is

small and should be weighted against much longer computation times

required for zero-pressure calculations.

Ch_03.qxd 11/29/04 6:08 PM Page 120

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 121

This issue is especially acute in first-principles calculations, where

embarking on expensive zero-pressure calculations may not be the best

strategy. Instead, the computational resources can be used for making a

constant-volume calculation on a larger supercell. If a highly accurate e

value is desirable, a number of constant-volume calculations can be per-

formed, followed by a linear extrapolation of the results to 1N → 0. It

should be remembered that, above a certain block size, most atoms are

residing in nearly perfect lattice positions. Therefore, any further increase

in the block size will only result in a better estimate of the elastic strain

energy of the slightly deformed lattice regions. Instead of modeling elas-

tic strains by first principles or atomistic calculations, it can be more

efficient to apply an extrapolation based on elasticity theory. These con-

siderations apply equally to interstitial atoms as well as any other point

defects in materials.

1.256

1.257

1.258

1.259

1.260

1.261

0.0 0.2 0.4 0.6 0.8 1.0

125200400800

Vacancy formation energy (eV)

V=const

p=0

Figure 3.1 Vacancy formation energy in copper as a function of the inverse num-

ber of atoms(N) in a cubic simulation block under constant-volume (V  const) and

zero-pressure (p  0) boundary conditions.

[61]

Calculations were performed with

an embedded-atom potential. The vacancy formation energy in a macroscopic

crystal is evaluated by a linear extrapolation to 1N

→ 0.The extrapolated value,

1.258 eV, does not depend on the boundary condition.

Ch_03.qxd 11/29/04 6:08 PM Page 121