Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials

Подождите немного. Документ загружается.

122 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

3.4 Harmonic Approximation

3.4.1 Harmonic Entropy of Point Defects

Besides point defect formation energies, their formation entropies

are another important ingredient required for calculating equilibrium

defect concentrations. The defect formation entropy is traditionally

attributed to perturbations of atomic vibrations in the defect core as

well as around it. The electronic entropy and other entropy effects can

also make contributions, but their role has not yet been examined in

much detail. As far as the vibrational entropy is concerned, its calcula-

tions are commonly based on the harmonic approximation to atomic

vibrations.

[62, 63]

In the harmonic approximation, the potential energy of a statically

relaxed simulation block is approximated by a Taylor series up to the

second-order terms with respect to small atomic displacements from

equilibrium. For a system containing N atoms, a 3N  3N dynamical

matrix,

iajb





∂x

∂

∂x



,(11)

is constructed, where E is the potential energy, x

is the displacement of

atom i in Cartesian direction a, and m

is the atomic mass. The normal

vibration frequencies of the block are determined as n

 l



, where l

are positive eigenvalues of the dynamical matrix. The total number M of

normal modes depends on the boundary conditions. A block with fixed

boundary conditions in all three directions has M  3N normal modes,

while for a supercell M  3N  3 because three vibrational modes are

replaced by translations of the center of mass.

[63]

Knowing the normal

vibration frequencies, the free energy G associated with atomic vibrations

at temperature T can be found from the standard quantum-mechanical

expression:

G  k

i1



2sinh



, (12)

where h is Planck’s constant and k

is Boltzmann’s factor. The vibrational

entropy S is readily obtained from this expression as the temperature

derivative, S ∂G∂T. In the commonly used classical approximation



m



Ch_03.qxd 11/29/04 6:08 PM Page 122

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 123

(all hn

 k

T), we have:

S k

i1

ln  Mk

. (13)

The entropy s

of vacancy formation in an elemental crystal is determined

as the entropy of a relaxed simulation block with a single vacancy minus

the entropy of a perfect lattice block containing the same number of

atoms. Importantly, because the two entropies refer to the same number of

vibrational degrees of freedom, the factors k

T and Mk

in Eq. (13) cancel

out, and s

turns out to be a temperature-independent quantity that only

depends on the relevant vibration frequencies:

k

ln .

(14)

Here, n

and n

represent normal vibration frequencies in the defected and

perfect crystal, respectively. This expression holds true for any point

defect as long as the classical harmonic approximation is at work. In the

quantum-mechanical regime (low temperatures), the defect formation

entropy does depend on the temperature.

3.4.2 Effect of Boundary Conditions on

Point-Defect Entropy

Like with the defect formation energy, the defect formation entropy also

depends on the choice of boundary conditions. In particular, the constant-

volume and zero-pressure relaxation schemes result in two different defect

formation entropies, which we denote as (s

)

and (s

)

, respectively. We are

usually interested in (s

)

in the context of diffusion calculations. It can be

shown that both (s

)

and (s

)

tend to their infinite-system values linearly in

1N as we increase the number of atoms in the block.

[61]

However, in con-

trast to the defect formation energy (which converges to the same value

regardless of the boundary condition), the two extrapolated entropies are

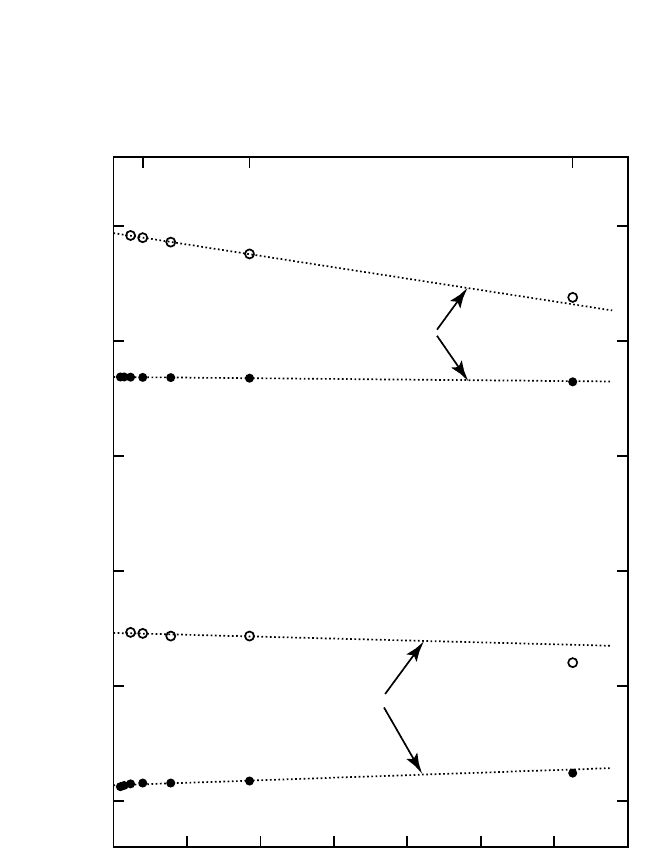
generally different. This fact is illustrated in Fig. 3.2 for a vacancy in copper.

Thus, even in an infinitely large system, the defect formation entropy

depends on the external conditions, and in particular is different under the

constant-volume and zero-pressure conditions. The difference between the



i1





i1



Ch_03.qxd 11/29/04 6:08 PM Page 123

124 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

0.5

1.0

1.5

2.0

2.5

3.0

0.0 0.5 1.0 1.5 2.0 2.5 3.0 3.5

32108500

Vacancy formation entropy / k

V=const

p=0

LHA

FHA

Figure 3.2 Vacancy formation entropy in copper as a function of the inverse num-

ber of atoms (N) in a cubic simulation block under constant-volume (V  const)

and zero-pressure (p  0) boundary conditions.

[61]

The vacancy formation entropy

in a macroscopic crystal is evaluated by a linear extrapolation to 1N

→ 0.

Calculations were performed with an embedded-atom potential in the full har-

monic approximation (FHA) and the local harmonic approximation (LHA).

Ch_03.qxd 11/29/04 6:08 PM Page 124

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 125

two entropies can be evaluated from well-known thermodynamic rela-

tions,

[64]

which lead to:

[60, 61, 65, 66]

)

 (s

)

 bB∆V, (15)

where ∆V is the relaxation volume of the defect formation, B is the bulk

modulus, and

b 



p0

(16)

is the thermal expansion coefficient of the material at zero temperature

and pressure. The latter can be readily determined by independent com-

putations.

[61]

Notice that for defects whose formation is accompanied by a

significant volume effect, the difference (s

)

 (s

)

can be quite large.

For example, it equals 1.7k

for a vacancy and 13.9k

for a self-interstitial

in copper.

[61]

To deduce the correct defect formation entropy, it is essential to per-

form the full (i.e., both atomic and volume) relaxation of the defected

block prior to the harmonic calculations. Alternatively, the volume can be

kept constant and (s

)

determined, but then (s

)

should be recovered

from Eq. (15). For point defects in Cu, the second scheme has proved to

be almost as accurate as the first.

[61]

3.4.3 Embedded Cluster Method

A major problem associated with harmonic calculations is their signifi-

cant computational cost. The calculation of the dynamical matrix for a simu-

lation block large enough to represent a defect still remains beyond the reach

of first-principles methods. Using interatomic potentials, the dynamical

matrix can be calculated relatively fast, but then the bottleneck of the compu-

tation shifts to its diagonalization. The diagonalization of a dynamical matrix

is a computationally demanding procedure which, for very large systems, is

associated with serious numerical problems. Because of this limitation, full

harmonic calculations become impractical beyond a certain block size (typi-

cally, N ≈ 10

). While for a single vacancy or other simple defect an accurate

formation entropy can be obtained with a few hundred atoms (Fig. 3.2), more

complex defects or defect clusters require more atoms. Anumber of approxi-

mate harmonic methods have been developed for dealing with large systems,

such as the embedded-cluster method,

[61, 67]

the local harmonic approxima-

tion,

[68]

the second-moment approximation,

[69–71]

and other methods.

[72]

∂V



∂T



Ch_03.qxd 11/29/04 6:08 PM Page 125

126 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

In the embedded-cluster method, only some of the free atoms, namely

those forming a cluster centered on the defect core, are treated as

dynamic; all other atoms are treated as static. Thus, the defect is created

and statically relaxed in a large simulation block, but the dynamical

matrix is only constructed and diagonalized for a relatively small cluster

embracing the defect. The defect formation entropy is then computed

using the dynamic atoms only. The elasticity theory analysis, as well as

atomistic simulations, show that the defect entropy S

delivered by the

embedded-cluster method equals approximately:

[61]

 S

 S

. (17)

Here, S

is the so-called defect core entropy, S

is the entropy associ-

ated with the elastic strain field around the defect, N

is the number of

atoms in the cluster, and N is the total number of atoms in the simula-

tion block. Given that the true formation entropy of the defect is

 S

 S

, we see that the cluster entropy S

is incomplete: it

includes only a part of the elastic strain entropy S

in proportion to

N. By calculating S

for several N

N values and extrapolating this

function to N

N → 0, we can determine the defect core entropy S

. The

latter turns out to be a well-defined physical quantity that does not

practically depend on the boundary conditions and characterizes the

degree of local distortions within the defect core. For example, in cop-

per S

 1.73k

for a vacancy and 5.75k

for an interstitial.

[61]

On the

other hand, the linear extrapolation to N

N → 1 should give us s

. In

practice, the accuracy of the obtained s

value is not very high because

Eq. (17) relies on strong approximations, including a spherical symme-

try of the elastic field around the defect.

Amore accurate scheme, called the “elastically corrected” embedded-

cluster method, has been proposed.

[61]

In this method, the cluster entropy

is augmented by a quasi-continuum term S

such that the sum of S

and

equals the true formation energy of the defect:

 S

 S

. (18)

The quasi-continuum term represents the entropy associated with the elas-

tic strain field outside the cluster. The calculation of S

is based on the

thermodynamic fact that the entropy density of a continuum (entropy per

unit volume) equals bp, where p is the local hydrostatic pressure

(negative of hydrostatic stress). This fact follows from the standard



Ch_03.qxd 11/29/04 6:08 PM Page 126

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 127

theromodynamic relation:

[64]



bV, (19)

where S is the system entropy and V is its volume. Based on this relation,

is represented by the sum:

b

Ω

, (20)

where p

and Ω

are hydrostatic pressures and atomic volumes associated

with individual lattice sites. The summation is performed over all atoms

outside the cluster. The product p

Ω

can be readily calculated within the

EAM scheme, as well as with any other semi-empirical potential. We

emphasize that Eqs. (18) and (20) are more general than Eq. (17). They

are not restricted to any symmetry and only require that the lattice strains

beyond the cluster be within the linear elasticity range. This general char-

acter makes the method applicable to point defects in GBs and disloca-

tions, to defect clusters, and to other complex situations.

This method again appeals to the idea that, in a large simulation block,

most atoms belong to elastically strained lattice regions whose direct

atomistic treatment is computationally inefficient. Instead, properties of

such regions (entropy, in this case) can be well represented in a continuum

approximation, while the highly distorted regions comprising the defect

cores are treated atomistically. We can notice a parallel with similar ideas

currently emerging in the area of multiscale modeling of materials.

Because the calculation of S

from Eq. (20) is a fast linear-N procedure,

the quasi-continuum term comes at almost no extra cost in comparison

with the cluster term S

. This computational advantage makes the method

applicable to very large systems, including those involving multiple

length scales. Simple tests

[61]

have demonstrated a high accuracy and

excellent computational efficiency of the method.

3.4.4 Local Harmonic Approximation

An even greater acceleration of entropy calculations can be achieved

by adopting the so-called local harmonic approximation (LHA).

[68]

In this

approximation, the off-diagonal terms of the dynamical matrix, which are

responsible for the coupling of vibrations of different atoms, are neglected:

iajb

 0, i  j. This reduces the dynamical matrix to a block-diagonal

form consisting of 3  3 blocks, each representing the local dynamical

∂S



∂p

Ch_03.qxd 11/29/04 6:08 PM Page 127

128 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

matrix D

with elements D

iaib

. The problem thus reduces to diagonalizing

the local dynamical matrix for each atom, or, equivalently, calculating its

determinant D

. For example, the classical entropy expression, Eq. (13),

in LHA becomes:

S 3k

i1

ln  3Nk

. (21)

In the second-moment method proposed by Sutton,

[69, 70]

the summa-

tions over the density of vibrational states are expressed through the local

second moments, m

 ∑

iaia

. Aslight modification of this method was

proposed by Foiles.

[71]

Although the derivation of the basic equations in

both cases proceeds along different lines in comparison with the LHA,

this boils down to neglecting even the diagonal elements of the local

dynamical matrices. This obviously means a more drastic approximation

than LHA.

An attractive feature of LHA and the second-moment methods,

besides their computational efficiency, is the feasibility of finding the

thermodynamic equilibrium of a system at a finite temperature by mini-

mizing its free energy with respect to all atomic displacements. This idea

has been implemented in the free-energy minimization method by LeSar

et al.

[68]

and through temperature-dependent interatomic forces by Sutton.

[69, 70]

Due to the relatively simple form of the free energy, analytical expressions

can be derived for its derivatives with respect to individual atomic coor-

dinates (thermodynamic forces), which enables the use of gradient methods

for minimizing the free energy. Unfortunately, the crude approximations

underpinning LHAand the second-moment methods inevitably result in a

significant loss of accuracy compared with the full harmonic scheme.

[71–73]

Taking a Cu vacancy as an example, LHA gives the vacancy formation

entropy (at zero pressure) a factor of two lower than the full harmonic

value (Fig. 3.2). Thus, when the free energy is minimized within LHA, the

optimized atomic coordinates can differ significantly from their true equi-

librium positions.

3.4.5 Quasi-Harmonic Approximation

For a perfect crystal, the full harmonic free energy can be readily min-

imized with respect to the crystal volume, thus giving the thermal expansion

factor at a chosen temperature. This minimization is easy to implement

due to its one-dimensional character. Indeed, the dynamical matrix and

thus the free energy can be computed for several volumes, and the free

hD



16



Ch_03.qxd 11/29/04 6:08 PM Page 128

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 129

energy minimum can be located by a polynomial interpolation. This

scheme is often referred to as the quasi-harmonic approximation

[71, 72]

emphasize that the anharmonicity-caused thermal expansion is evaluated

through harmonic calculations. Unfortunately, an extension of this

scheme to a simulation block containing a defect is problematic. Since

thermal expansion is then nonuniform, the free energy should be mini-

mized with respect to all atomic positions, a problem too ambitious for

today’s computers. As a rough approximation, a statically relaxed simula-

tion block can be simply expanded uniformly by the thermal expansion

factor of the perfect lattice, followed by the construction of the dynamical

matrix and calculation of the defect formation entropy.

[71]

This way of

including the thermal expansion into the defect formation entropy has

proved to work well in some cases

[71, 74]

but fails in other cases where some

of the eigenvalues of the dynamical matrix after the expansion become neg-

ative. Such failures are not surprising since the neglect of the local thermal

expansion in the defect core introduces an uncontrollable approximation.

There are methods of thermodynamic calculations beyond the har-

monic approximation. Perhaps the most common of them are various

thermodynamic integration schemes

[56, 72]

and the adiabatic switching

method,

[75, 76]

which can be implemented within either Monte Carlo or MD

simulations. Such methods have been applied to calculate the formation

entropy of point defects in metals

[71, 76]

and intermetallic compounds.

[77]

Although very powerful, such methods require extremely extensive com-

putations for achieving a reasonable accuracy. They are also useful as a

reference for assessing the applicability range of harmonic methods. As

expected, deviations between harmonic and “exact” methods are observed

at high temperatures, often already above half of the melting temperature.

The onset temperature and degree of such deviations depend on the par-

ticular defect type, the atomic interaction model, and other factors.

[72]

3.5 Equilibrium Defect Concentrations

3.5.1 Elemental Solids

The knowledge of the formation energies and entropies of point

defects is required for calculating their equilibrium concentrations. For

example, the equilibrium vacancy concentration (number of vacancies per

lattice site) in an elemental solid at temperature T is given by:

 exp













. (22)

Ch_03.qxd 11/29/04 6:08 PM Page 129

130 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

A similar equation holds for self-interstitials and other simple defects,

except that a pre-exponential factor z should be introduced to reflect the

entropy arising from the multiplicity of possible orientations of the defect.

For example, a self-interstitial in fcc metals typically exists as a split

dumbbell centered on a lattice site. The dumbbell possesses an additional,

“rotational” entropy k

ln z, z being the number of its symmetrically

equivalent orientations. Thus, the concentration of a general point defect

can be written as:

c  z exp







. (23)

Factor z is often eliminated by including the term k

ln z into the defect

formation entropy s

. Another way of writing Eq. (23) is:

c  exp







, (24)

where

 e

 Ts

(25)

is the free energy of defect formation. At this point, we assume that the

external pressure is zero. The effect of high pressures on defect concen-

trations is discussed in Sec. 3.5.3.

3.5.2 Non-Stoichiometric Compounds

The situation is more complex in ordered compounds due to the inher-

ent multiplicity of point defects.

[39, 78–80]

Vacancies can occupy different

sublattices and thus have different formation energies and entropies.

Compounds are also able to support antistructural atoms, or antisites

(atoms occupying the wrong sublattice), and in some cases also intersti-

tials. Since all point defects should be in equilibrium with each other, the

vacancy concentration cannot be determined separately without considering

all other defects. In other words, even if we are only interested in the

vacancy concentration, we still have to solve the problem of global

dynamic equilibrium in the entire defect system.

As an example, consider an equiatomic intermetallic compound AB.

We assume that the structure of this compound consists of two sublattices



 Ts



Ch_03.qxd 11/29/04 6:08 PM Page 130

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 131

a and b, which in the perfectly ordered state are occupied by atoms Aand

B, respectively. The compound can support four types of point defects:

vacancy on sublattice a (V

), vacancy on sublattice b (V

), antisite on

sublattice a (B

), and antisite on sublattice b (A

). Interstitial atoms are

neglected for simplicity. The creation of each point defect slightly changes

the chemical composition of the compound. The latter, therefore, depends

on all four defect concentrations and can deviate from the exact stoichio-

metric composition. Statistical models describing the defect equilibrium

in compounds normally treat point defects as a lattice gas of noninteract-

ing particles.

[39, 78–80]

In our case, we deal with a four-component gas. The

particles of the gas can only interact through defect reactions, which are

similar to chemical reactions in a real gas. For example, an exchange of a

regular atom B with a neighboring vacancy V

is represented by the defect

reaction:

∆ B

 V

. (26)

The equilibrium in the defect gas can be described by writing the mass

action law for three independent reactions.

[80]

The fourth equation

expresses the constraint that the defect concentrations should match a par-

ticular chemical composition of the compound. These four simultaneous

equations are solved numerically for four equilibrium defect concentra-

tions. That way, the defect concentrations can be computed as functions

of the chemical composition and temperature. The input data for this cal-

culation are the free energies of the chosen defect reactions. These can be

expressed by linear combinations of the respective formation free energies

of the defects involved in the reactions.

Instead of dealing with individual point defects, it is more convenient

to introduce hypothetical composition-conserving defect complexes.

[39, 78]

For example, the formation of a divacancy V

 V

or an exchange defect

 A

does not change the chemical composition of the compound.

Such complexes are assumed to be totally dissociated, so that interactions

between their constituent defects can be neglected. The advantage of deal-

ing with composition-conserving complexes is that all reference constants

involved in the energies and entropies of individual defects always cancel

out when combined into a complex energy or entropy.

[78]

This allows

direct comparison of results obtained by different calculation methods, for

example by EAM and first-principles calculations.

The language of composition-conserving complexes also has certain

conceptual advantages that have been well discussed in the literature.

[39]

Point defects can be thought of as appearing and disappearing in the form

of such complexes. Furthermore, the complexes can be viewed as ele-

mentary excitations of thermal disorder that follow Boltzmann’s distribution.

Ch_03.qxd 11/29/04 6:08 PM Page 131