Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials

Подождите немного. Документ загружается.

142 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

elastic forces normal to it are eliminated at each step of the relaxation. It

turns out that the relaxed elastic band positions itself approximately along

the MEP and thus passes through the saddle point

[98, 99]

[Fig. 4.4(b)]. The

image with the highest potential energy is, therefore, taken as an approxi-

mation to the saddle point. The latter can be located more precisely by

applying an interpolation of atomic coordinates between the highest energy

image and its neighbors. More sophisticated schemes of refining the saddle-

point position have been developed, such as the climbing-image NEB

method.

[100]

The crucial advantage of the NEB method is that it imposes no

restriction on the number of atoms participating in the transition, which

makes it suitable for collective jumps.

The elastic band typically contains 10 to 15 images. In some cases, as

few as 5 to 7 images were sufficient for obtaining accurate results.

[100]

the other hand, if the energy landscape is complex and it is important not to

miss a hidden minimum along the transition path, as many as 25 to 30

images can be used.

[101]

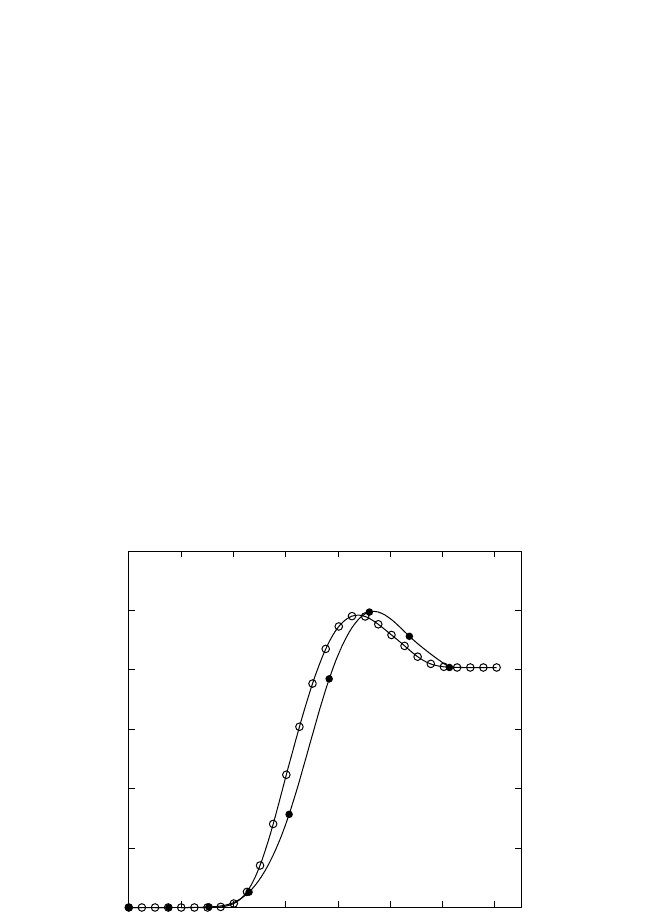
Figure 3.5 illustrates two NEB calculations with two

different numbers of images. Both calculations were made for the same col-

lective [110] vacancy jump of a Ni vacancy in NiAl

[101]

(Fig. 3.6). The two

0.0

0.5

1.0

1.5

2.0

2.5

3.0

0 1 2 3 4 5 6 7

Energy (eV)

Reaction path (A

)

Figure 3.5 Energy along the reaction path of the collective [110] nearest-neighbor

jump of a Ni vacancy in NiAl.The curves were calculated with 7 images (

•) and 27

(

) images.

[101]

The energy is measured relative to the initial state of the vacancy

and the distance along the reaction path is the Euclidian distance between neigh-

boring images in the configuration space of the system.The simulation block con-

tains 1024 atoms, and the EAM potential

[6]

was used.

Ch_03.qxd 11/29/04 6:08 PM Page 142

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 143

jump barriers are rather close to each other, as are the respective saddle-

point structures.

The NEB method has proved to be highly robust in recent studies of

diffusion in intermetallic compounds

[101]

and grain boundaries.

[92, 93]

Other, more sophisticated methods of saddle-point search have also

been proposed.

[98]

In particular, the dimer method is capable of finding

a saddle point without knowing the final state of the transition.

[102]

far, most of such new methods have not been well tested for bulk diffu-

sion in solids, but applications to surface diffusion show promising

results.

[98, 102, 103]

3.7 Kinetic Monte Carlo Simulations

3.7.1 Basic Idea of the Method

Kinetic Monte Carlo (KMC) simulations present a very powerful

method for modeling diffusion processes.

[104, 105]

We will explain the idea

of the method by considering diffusion mediated by the random walk of a

single point defect. The potential energy surface of the system (Fig. 3.4)

has a large number of local energy minima, each corresponding to a dif-

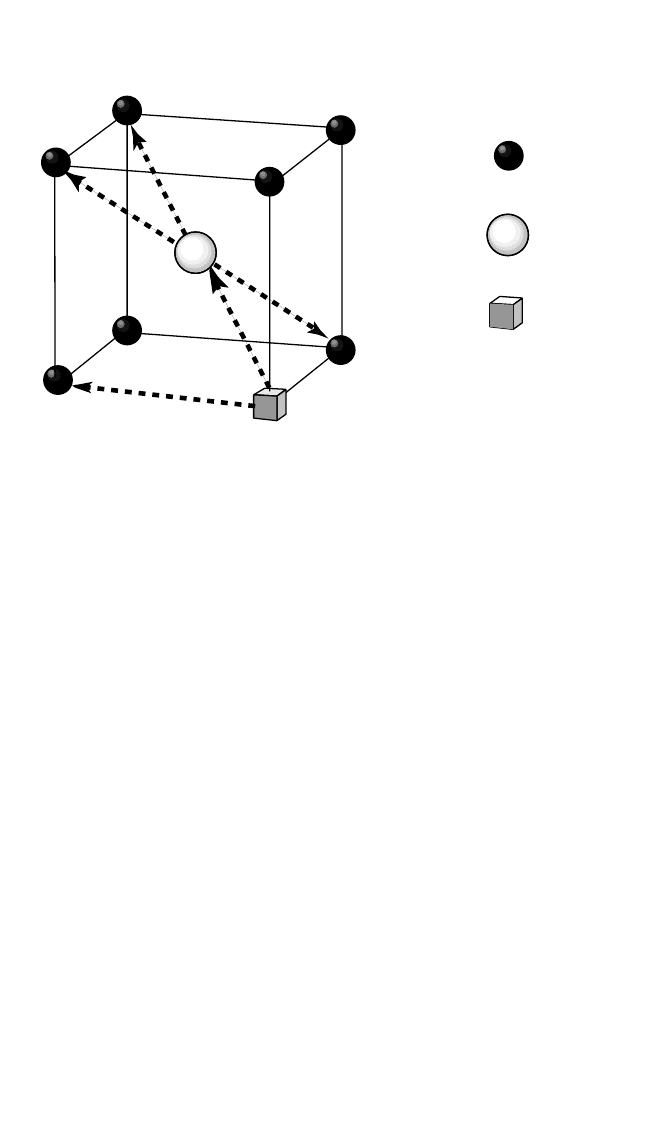
NNN

Vacancy

2''

Figure 3.6 Geometry of Ni vacancy jumps in NiAl. NNN: next-nearest neighbor

jump; 1-2, 1-2 and 1-2: collective jumps by vectors [110], [100], and [111],

respectively.

[101]

Ch_03.qxd 11/29/04 6:08 PM Page 143

144 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

ferent position of the defect. Suppose for every equilibrium state i, we

know the transition rates Γ

to all other states j. The set {Γ

} is called the

rate catalog of the diffusion process. We then create a single defect in the

simulation block and let it walk by jumping from state to state. For each

state i, we determine the residence time,

 ,

(44)

and the probabilities of all transitions from that state,

 Γ

. (45)

One transition is selected by dividing a unit interval into segments

of lengths P

and generating a random number with a uniform distribu-

tion on this interval. The transition is implemented by updating atomic

coordinates according to the diffusion mechanism, the clock is

advanced by t

, and the process continues from the new state. Periodic

boundary conditions are usually applied to the simulation block, so that

if the defect attempts to jump out of the block, it reappears on its oppo-

site border. As the defect walks through the system, it moves atoms

around and thus induces their diffusion. After a long defect walk, the

diffusion coefficient D

in a chosen direction x is calculated from the

average squared displacement of all atoms. Namely, using Einstein’s

relation, we have:

 x . (46)

Here, X

is the x-component of the displacement of atom k from its initial

position, N is the number of atoms in the block, and t is the accumulated

simulation time.

Notice the important factor x in Eq. (46). This factor makes a cor-

rection for the fact that during the simulation, we always have exactly

one defect in the block, whereas in equilibrium conditions, the block

would contain, on average, x  Nc defects, c being the equilibrium

defect concentration (Sec. 3.5). We assume that the latter is small and

that each point defect moves atoms independently of other defects.

Then, the diffusion coefficient calculated with one defect should be

N



j≠i

Ch_03.qxd 11/29/04 6:08 PM Page 144

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 145

multiplied by the factor x. Eq. (46) can be conveniently rewritten in

the form

 c. (47)

To improve the accuracy of the calculation, the defect walk is repeated

many times starting from different configurations, and the results are aver-

aged. Other precautions include making sure that the average value of X

close to zero (no drift in the absence of external forces) and checking the

convergence with respect to other factors such as the block size.

The KMC method is extremely fast and accurate. Since every jump

attempt results in a transition, millions of Monte Carlo steps per atom can

be readily accumulated, resulting in a high accuracy of the diffusion coef-

ficient. The jump correlation effects are automatically incorporated in the

calculation, which removes the necessity of knowing the correlation fac-

tors. In fact, KMC simulations are often used as a means of calculating

jump correlation factors.

[104, 106]

However, the speed and accuracy of the

method come at a price. (1) The KMC method only applies to systems that

can be mapped onto a lattice. This leaves amorphous solids, complex

defect structures in crystals, and many other disordered or long-period

structures beyond the reach of the method. (2) The diffusion mechanisms

operating in the system should be known in advance. In many situations,

diffusion mechanisms are either unknown or very complex. GBs and sur-

faces offer a wealth of examples where multiple diffusion mechanisms

can be operative, including collective events that can hardly be guessed a

priori. In such systems, compiling a reasonably complete rate catalog can

be a challenging problem. (3) The KMC method is not easy to apply to

binary or multicomponent alloys and compounds. Even though diffusion

in such alloys is likely to occur by the simple vacancy mechanism, the

vacancy jumps are environmentally dependent. Creating a catalog of jump

rates for all possible atomic permutations even within a few coordination

shells around a vacancy would be an overwhelming task, not to mention

the possible effect of long-range interactions.

[107]

3.7.2 Grain Boundary Diffusion

Grain boundary diffusion in metals is an area where KMC simulations

have been particularly useful. GBs provide high-diffusivity paths in mate-

rials and control many processes at elevated temperatures, such as



Ch_03.qxd 11/29/04 6:08 PM Page 145

146 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

microstructural evolution, phase transformations, Coble creep, and

sintering.

[108]

The difference between the GB and lattice diffusion coeffi-

cients in the same material can easily reach 6 to 8 orders of magnitude.

This interesting phenomenon has been known and extensively studied for

five decades.

[95, 108–111]

While a large amount of experimental data has been

accumulated over the years, an atomistic understanding of GB diffusion

has been in a rudimentary state until very recently. Significant progress

in gaining such understanding has been achieved through computer

modeling.

[92–95, 112–120]

It has been established that GBs readily support both vacancies and

interstitials. The interaction of these defects with GBs is short-range and

is limited to a few atomic layers around the GB plane. Within the GB core

region, the vacancy and interstitial formation energies are on average

lower than in the bulk, but their variations from site to site are remarkably

large. For example, the vacancy formation energy can be as low as 10%

of the bulk value at some sites and above the bulk value at other

sites.

[92, 93, 112, 113]

The low average values and large site-to-site variations of

point defect formation energies reflect specific features of the GB struc-

ture. The latter is on average more open than the regular lattice

[121]

but

contains alternating regions of compression and expansion. It is those

regions that give rise to the strong variations in the defect formation

energy. Furthermore, in contrast to the bulk situation, the formation ener-

gies of vacancies and interstitials are very close to one another, which

makes both defects equally important for diffusion and other properties of

GBs. Atomistic simulations

[92, 93, 112, 113]

have revealed new interesting

structural forms of point defects in GBs. Vacancies can be localized at cer-

tain GB sites (as they are in the lattice), but in many cases they can delo-

calize over a relatively large area. Many GB sites do not support a stable

vacancy at all: the vacant site is spontaneously filled by a neighboring

atom during the static relaxation process. The vacancy delocalization and

instability can be explained by the existence of strong stress gradients

between adjacent compression and tension regions within the GB

core.

[112, 113]

Likewise, interstitial atoms can be localized in interstices, but

they often form split dumbbell configurations or highly delocalized dis-

placement zones reminiscent of crowdions.

[92, 93, 112, 113]

Given this multi-

plicity of structures and energies of point defects, it is not surprising that

GBs support a large variety of diffusion mechanisms, many of which are

collective displacements of several atoms. Such mechanisms, as well as

the methods by which they were found, are discussed in Sec. 3.8.2.

Figure 3.7 shows the temperature dependence of GB diffusion coeffi-

cients calculated by the KMC method for a few symmetrical tilt GBs in

Cu.

[92]

The KMC code used in the calculations was general enough to

accommodate diffusion mechanisms of any complexity, including collective

Ch_03.qxd 11/29/04 6:08 PM Page 146

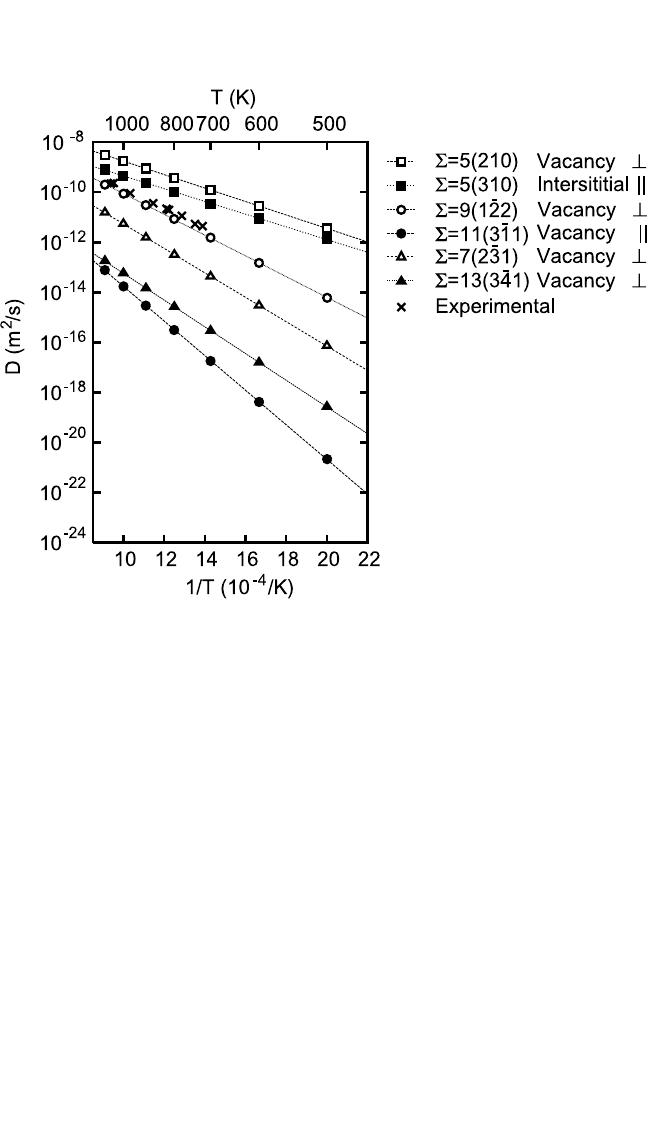
ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 147

Figure 3.7 Arrhenius plot of grain boundary diffusion in copper obtained by KMC

simulations.

[92]

Only diffusion in the fastest direction in each boundary is shown in

this plot. The fastest direction (

⊥, normal to the tilt axis; ;, parallel to the tilt axis)

and the dominant point defect are indicated in the legend. Experimental diffusion

coefficients measured on polycrystalline samples

[122]

are shown for comparison.

transitions induced by either vacancies or interstitials, transitions between

localized and delocalized states of point defects, and other events. To

obtain each diffusion coefficient, up to 10

Monte Carlo steps were made

to guarantee the convergence of the results. Because the vacancy and

interstitial mechanisms were simulated separately, the relative importance

of the two defects could be evaluated. Figure 3.7 demonstrates that the

Arrhenius Law is followed by the diffusion coefficients very accurately,

despite the involvement of many diffusion mechanisms with different

activation energies. The effective activation energy was determined by

numerically fitting the Arrhenius relation to the calculated diffusion coef-

ficients. The effective activation energy was often found to correlate with

the activation energy of a particular defect jump, suggesting that this jump

dominated the overall diffusion process. Interestingly enough, the domi-

nant diffusion jump was not necessarily the one with the lowest activation

Ch_03.qxd 11/29/04 6:08 PM Page 147

148 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

energy. The latter is quite understandable. In order to contribute to long-

range diffusion, the jumps should form a penetrating network through the

GB structure. It was not uncommon to find jumps that had a low activa-

tion energy but were isolated from each other. Such jumps, then, did not

effectively contribute to diffusion, but rather slowed it down by acting as

traps. Furthermore, under the vacancy mechanism, isolated chains of easy

jumps did not contribute to diffusion. This is consistent with the known

fact that the correlation factor of one-dimensional diffusion is zero.

[118]

Figure 3.7 also demonstrates that diffusion in some GBs is dominated

by vacancies and in others by interstitials. Thus, there is no unique mech-

anism of GB diffusion: either vacancies or interstitials can dominate,

depending on the GB structure. The diffusion coefficients are anisotropic,

which reflects the structural anisotropy of tilt GBs. Note that the fastest

diffusion direction can be either parallel or perpendicular to the tilt axis.

The latter observation seems to contradict the experimental measurements

suggesting that diffusion parallel to the tilt axis is always faster.

[108]

Note,

however, that the calculations were made for ideal singular boundaries

with relatively low Σ values (Σ being the reciprocal density of coincidence

sites). The real GBs studied in experiments are likely to be vicinal and

contain secondary GB dislocations running parallel to the tilt axis. Such

dislocations are able to enhance diffusion in the parallel direction.

Another remarkable effect evident from Fig. 3.7 is the broad range of

GB diffusivities found in the same material. Depending on the GB struc-

ture, the diffusivity varies by almost four orders of magnitude even at high

temperatures. Notice that the experimental data measured on polycrys-

talline samples

[122]

lie well within the calculated range, closer to its upper

part. We are led to conclude that the concept of an average, or general,

GB, whose diffusivity is measured in polycrystalline materials, is quite

loose. This conclusion emphasizes the importance of experimental

measurements on bicrystals containing individual, well-characterized

GBs.

[95, 108,109]

On the computational side, an interesting problem for future

research would be to calculate GB diffusion as a function of misorienta-

tion around a low-Σ boundary and compare the results with experimental

data. Another interesting topic is the effect of segregated atoms on GB dif-

fusion. It is very likely that GB segregation can alter not only the diffu-

sion rates but also the diffusion mechanisms. This possible effect has not

been studied in much detail.

The KMC method has been widely applied to surface diffusion, an area

where the multiplicity and complexity of diffusion mechanisms is a well-

established notion.

[89, 98, 103]

Qin and Murch

[123]

simulated diffusion along a

dislocation core by a postulated vacancy mechanism. Although their dislo-

cation model was simplistic and the simulations did not address any specific

material, useful insights into possible jump correlation effects were obtained.

Ch_03.qxd 11/29/04 6:08 PM Page 148

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 149

3.7.3 Diffusion in Alloys and Compounds

Another area of KMC simulations is diffusion in disordered and

ordered bulk alloys. As far as disordered alloys are concerned, the sim-

plest KMC model, which has been widely used since the 1970s, is based

on the two-frequency approximation. This model describes vacancy dif-

fusion in a random binary alloy A-B with a rigid lattice (Ising model) in

terms of two parameters: the vacancy exchange rates with atoms A (w

)

and B (w

). Dozens, if not hundreds, of KMC simulations within this

model have been published. We will not review that large area since we

want to focus on models based on realistic atomic interactions in materi-

als. We should mention, however, that this simple model has been

extremely useful in clarifying many general issues of diffusion kinetics in

solids, including jump correlations and their relationship to phenomeno-

logical coefficients.

[104, 124]

An appealing feature of this model is that it

underpins many analytical models, which typically also treat alloy diffu-

sion in terms of two-jump frequencies, w

and w

[104, 124–126]

The only dif-

ference is that KMC simulations offer an exact numerical solution of the

problem, whereas analytical models introduce further approximations

aimed at simplifying the problem to the extent that it can be solved in a

closed form. This makes KMC simulations a useful testing ground for

analytical theories, including the classical Manning theory of diffusion in

a random alloy.

[126]

Extensive KMC simulations within the two-frequency

model, together with the concurrent development of analytical models,

were pioneered by Murch

[104]

and are now indisputably led by Belova and

Murch.

[127–130]

For diffusion in ordered compounds, the two-frequency model can be

extended to include more frequencies representing vacancy exchanges

with atom A or B depending on whether the vacancy and atom are resid-

ing on the same or opposite sublattices. In the simplest case of a B2-

ordered compound, only four jump frequencies are introduced: w

, w

and w

, where the superscript indicates the sublattice occupied by the

vacancy. By varying ratios of these frequencies, qualitatively different sit-

uations can be reproduced, including strongly and weakly ordered com-

pounds, the vacancy preference to one sublattice or another, and different

off-stoichiometries. Extensive KMC simulations within this model have

largely contributed to the understanding of the anti-structural bridge

mechanism,

[131]

six-jump vacancy cycles,

[132, 133]

and the effect of long-

range order on the ratio of the tracer diffusivities of atoms A and B.

[134]

A more advanced model, which was applied to both ordered and dis-

ordered alloys, addresses the alloy energetics within the Bragg-Williams

approximation. It describes atomic interactions on a rigid lattice in terms

of nearest neighbor bonds and is based on three energetic parameters: e

Ch_03.qxd 11/29/04 6:08 PM Page 149

150 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

, and e

. It is more convenient, however, to analyze the model in terms

of two reduced parameters: ek

T and uk

T, where e  e

 e

 2e

is the ordering energy and u  e

 e

is the asymmetry energy. The

configurational entropy is treated within the mean-field approximation.

By adjusting the parameters ek

T and uk

T, various types of phase dia-

grams can be simulated, from one with a miscibility gap to a series of

ordered compounds.

[135]

For the modeling of diffusion processes, the

vacancy formation energy is identified with the energy of broken bonds

when removing an atom from the lattice. The rate of vacancy exchange

with an atom is postulated in the Vineyard form, Γ  n

exp(e

k

T),

where e

is an environmentally dependent activation energy. The latter is

represented in the form:

 e

 e

, (48)

where e

is the total energy of all bonds of the atom exchanging with the

vacancy (i.e., bonds that will be broken by the jump), and e

is the energy

at the saddle point. For simplicity, e

and n

are usually assumed to be con-

stant. This approximation for e

can be traced back to Kikuchi and

Sato,

[136]

but it was probably Martin and co-workers

[137–139]

who put it into

a KMC algorithm and applied to a variety of alloy simulations. Using this

or similar approaches, Athènes et al.

[138]

and, more recently, Belova and

Murch

[132, 140, 141]

examined diffusion mechanisms in ordered intermetallic

compounds, particularly six-jump cycles and anti-structural bridges. Note

that the KMC scheme based on Eq. (48) does not require any rate catalog

since the jump rates are computed at each step of the simulation, depend-

ing on the local environment of the vacancy. This scheme, therefore, can

be viewed as a particular case of on-the-fly Monte Carlo simulations

discussed in Sec. 3.7.4.

Although the previously discussed KMC schemes have largely

contributed to solving general issues of diffusion kinetics, the drastic

approximations underlying these schemes prevent them from producing

quantitatively meaningful results for specific materials. The Bragg-

Williams approximation does not capture alloy thermodynamics on a

quantitative level. Perhaps more importantly, Eq. (48), especially with

 const and n

 const, hardly has a sound physical justification.

Further improvements of such schemes can be sought. For example, the

broken-bond energy of the atom in the final state can be added to Eq. (48)

with some weight. The attempt frequency can be correlated with the acti-

vation energy using Zener’s relation lnn

 e

[142]

Such improvements,

however, are unlikely to elevate these calculations to a quantitative level.

Bocquet

[107]

has recently examined many of the approximations and

empirical correlations commonly used in KMC simulations. He performed

Ch_03.qxd 11/29/04 6:08 PM Page 150

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 151

extensive calculations of vacancy formation and migration energies, as

well as the relevant attempt frequencies, in disordered Au-Ni alloys. His

calculations were based on molecular statics and the harmonic approxi-

mation, with atomic interactions described by many-body potentials of the

second-moment approximation (similar to EAM). He found no strong cor-

relation between e

and site occupations within the first four coordina-

tion shells around a vacancy. Keeping the composition of that region fixed

and changing site occupations beyond that region, significant variations

(up to a factor of two) in e

could be readily produced. This observation

emphasizes the critical importance of atomic relaxations and long-range

interactions, which are totally neglected in existing KMC schemes. The

 const approximation was also examined by Bocquet

[107]

and was

found not to work with any reasonable accuracy. Zener’s correlation was

found to hold as a general trend, but n

values could easily deviate from

the correlation line by two orders of magnitude on either side.

Finally, we should mention the brief interest in KMC simulations of

diffusion and ionic conductivity based on a large rate catalog generated by

the static relaxation method.

[143, 144]

The catalog was constructed by includ-

ing a variety of possible environments of a vacancy. To our knowledge,

after the initially successful calculations of ionic conduction in Y-doped

CeO

[144]

the work in that direction was not continued.

3.7.4 On-the-Fly Monte Carlo Simulations

The main limitation of the KMC method arises from the necessity of

having a rate catalog before starting a simulation. Even after putting a lot

of effort into constructing a large catalog, we can never be sure that all

important diffusion mechanisms have been included. Therefore, the atom-

istic simulation community has been motivated to search for more flexi-

ble Monte Carlo schemes, particularly self-learning algorithms in which

the possible escape paths from every equilibrium state are identified in the

course of the simulation. A few such algorithms have been proposed and

are often referred to as on-the-fly Monte Carlo (OFMC).

Taking diffusion in alloys as an example, the most straightforward

(although not necessarily the most efficient) OFMC scheme could be

described as follows.

[107, 145]

We postulate that (1) the crystal structure of

the alloy is preserved during the diffusion process; (2) diffusion takes

place by the vacancy mechanism; and (3) vacancy jumps follow harmonic

TST. Then, for each vacancy position, we try all zpossible exchanges with

the nearest neighbors, z being the coordination number of the lattice. For

each possible exchange, we find the saddle point (using the NEB or the

drag method), the jump barrier e

, the attempt frequency n

, and thus the

Ch_03.qxd 11/29/04 6:08 PM Page 151