Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials

Подождите немного. Документ загружается.

132 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

One of the complexes usually dominates all others, although this leading

complex may change with temperature and/or pressure. Dealing with

composition-conserving complexes means making a judicious choice of

the defect reactions. The reactions should conserve the chemical composi-

tion and describe the creation (annihilation) of the chosen defect com-

plexes. For example, the three reactions can be chosen as the divacancy

(Dv) formation:

 V

∆ 0, (27)

the exchange defect (Ex) formation:

 A

∆ 0, (28)

and the triple-defect formation on the a sublattice (TA),

 A

∆ 0. (29)

In these reactions, 0 denotes the ground state of the compound (perfect lat-

tice). The free energies of these reactions represent the formation free

energies of the respective defect complexes (Dv, Ex and TA). The free

energy of each complex is found by combining the formation free ener-

gies of individual defects, each obtained by a separate calculation, accord-

ing to the formula of the reaction. For example, the free energy of an

exchange defect equals g

 g

 g

. Similar rules apply to energies

and entropies of defect complexes. Thus, the energy of a triple defect, TA,

equals e

 2e

 e

. Remember that the formation energy and entropy

of an individual defect are defined here under the condition of a constant

number of atoms.

As an illustration of such calculations, Table 3.1 presents the formation

energies and entropies of several defect complexes in the intermetallic

compounds TiAl and NiAl.

[6, 81]

The crystal structures of these compounds

are L1

(CuAu prototype) and B2 (CsCl prototype), respectively. These

compounds demonstrate two different mechanisms of non-stoichiometry

that are discussed next. They also represent promising structural materials

for advanced high-temperature applications, particularly in the aerospace

industry.

[82, 83]

The entropies listed in Table 3.1 were computed in the clas-

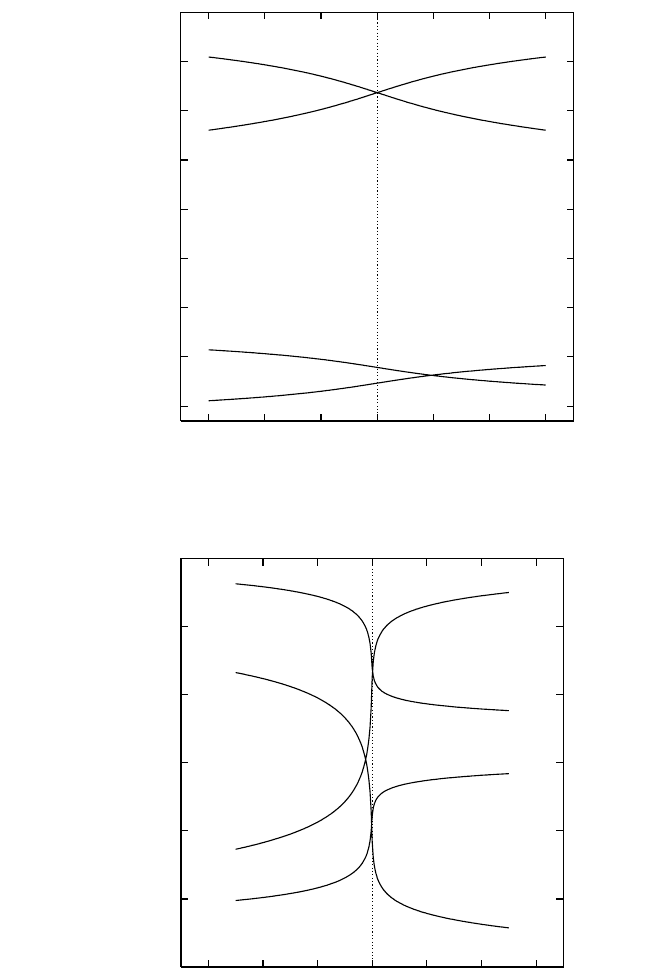
sical harmonic approximation. Figure 3.3 shows the calculated composi-

tion dependencies of the point defect concentrations in these compounds

(number of defects per lattice site). We observe that TiAl is strongly dom-

inated by antisites Ti

and Al

for all compositions, whereas the vacancy

concentrations are relatively small. In contrast, in the NiAl compound, the

antisites Ni

and vacancies V

are the dominant defects; other defect

Ch_03.qxd 11/29/04 6:08 PM Page 132

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 133

concentrations are orders of magnitude smaller. These observations are in

agreement with previous calculations performed by neglecting defect

entropies but using first-principles defect energies.

[39, 84]

Constitutional point defects in compounds are an important concept.

At low temperatures, a deviation of the chemical composition from the

stoichiometry is accommodated by a certain type of point defect, which is

called constitutional. Constitutional defects are conceptually different

from thermal defects. The latter are thermally excited and only exist at

elevated temperatures due to the configurational entropy of the com-

pound. In contrast, constitutional defects exist at any temperature and

serve to maintain the particular off-stoichiometric composition of the

compound. If we gradually decrease the temperature at a fixed composi-

tion, the concentrations of all thermal defects will go to zero, while the

concentration of constitutional defects will remain constant and will only

depend on the composition. In other words, constitutional defects are what

is left when all thermal defects freeze out. Clearly, constitutional defects

only exist in off-stoichiometric compositions. Importantly, the type of

constitutional defect can be different in different compounds, and in each

compound can be different on either side of the stoichiometry.

For example, in TiAl, the off-stoichiometry is accommodated by Ti

antisites on the Ti-rich side and Al

antisites on the Al-rich side. Thus, the

antisites are the constitutional defects. The antisites are also the dominant

thermal defects in this compound [Fig. 3.3(a)]. Both facts have one common

origin: the exchange defect Ti

 Al

is the most favorable composition-

conserving defect complex in TiAl (Table 3.1). This explains why antisites

are excited most easily by thermal fluctuations and are readily available

to accommodate the off-stoichiometry. Such compounds are classified as

antisite-disorder type.

Table 3.1. Energies and Entropies of Composition-Conserving Point Defect

Complexes in the Intermetallic Compounds TiAl

[81]

and NiAl

[6]

Calculated

with Embedded-atom Potentials. Defect Complexes: Ex, Exchange Defect;

Dv, Divacancy; TA, Triple Defect on the a Sublattice; TB, Triple Defect on

the b Sublattice.

TiAl NiAl

Notation Complex Energy (eV) Entropy (k

) Energy (eV) Entropy (k

)

Ex A

 B

0.765 1.420 2.765 4.903

Dv V

 V

3.168 2.804 2.396 2.965

TA 2V

 A

3.525 3.952 2.281 3.588

TB 2V

 B

3.576 3.075 5.276 7.245

Ch_03.qxd 11/29/04 6:08 PM Page 133

134

-8

-7

-6

-5

-4

-3

-2

-1

44 46 48 50 52 54 56

at.% Ti

Defect concentration

-12

-10

-8

-6

-4

-2

44 46 48 50 52 54 56

at.% Ni

Defect concentration

(a) TiAl

(b) NiAl

Figure 3.3 Equilibrium point-defect concentrations in TiAl

[81]

and NiAl

[6]

at 1000 K.

These plots illustrate two different mechanisms of atomic disorder in compounds:

the antisite mechanism (TiAl) and the triple-defect mechanism (NiAl).

Ch_03.qxd 11/29/04 6:08 PM Page 134

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 135

In contrast, in NiAl, it is the triple defect 2V

 Ni

that is the most

favorable defect complex (Table 3.1). This makes V

vacancies and Ni

antisites the dominant thermal defects [Fig. 3.3(b)]. Furthermore, being

most easily available, these defects also serve as constitutional defects,

with Ni

antisites appearing on the Ni-rich side and V

vacancies appear-

ing on the Al-rich side. The existence of constitutional Ni vacancies in

Al-rich NiAl was confirmed experimentally.

[85]

Intermetallic compounds

with this mechanism of disorder are called triple-defect type. Besides

NiAl, they are represented by the B2 compounds CoAl and CoGa.

To further demonstrate the convenience of the defect-complex

approach, we will derive approximate expressions for point defect con-

centrations in stoichiometric TiAl and NiAl. For the antisite-disorder

compound TiAl, in a first approximation we can neglect the vacancies and

consider antisite defects only. Then, the concentrations of both antisites

are equal. The mass action law for the exchange defect reaction (28),

 exp







, (30)

immediately gives us

 c

 exp







. (31)

At the next step, we write the mass action law for the triple-defect

reaction (29),

 exp







Substituting c

from Eq. (31), we obtain the Ti vacancy concentration:

 exp







. (32)

By simply swapping the species in this equation, we immediately obtain

the Al vacancy concentration:

 exp







, (33)

 g



 g





Ch_03.qxd 11/29/04 6:08 PM Page 135

136 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

where, g

is the free energy of the triple defect TB  2V

 Al

on the

Al sublattice. Using the obvious relation g

 g

 2g

 g

, we can

rewrite Eq. (33) in a different form:

 exp







. (34)

These equations allow us to calculate all four defect concentrations given

three complex free energies: g

, g

and g

Turning to NiAl, we proceed along similar lines. We first consider the

dominant defect reaction, Eq. (29), and neglect the concentrations of V

and Al

. Then, we have c

 2c

, and the mass action law,

 exp







, (35)

gives us

 2

13

exp







(36)

and

 2

23

exp







. (37)

Knowing the major defect concentrations, we determine the minor ones.

From the divacancy reaction, Eq. (27), we easily obtain:

 2

13

exp







. (38)

Similarly, the exchange reaction, Eq. (28), gives us

 2

23

exp







. (39)

 g



 g





 g

 2g



Ch_03.qxd 11/29/04 6:08 PM Page 136

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 137

Again, the four defect concentrations are expressed through three

complex free energies g

, g

, and g

. Remember that all defect concen-

trations in Eqs. (30) through (39) are measured relative to the respective

sublattices. They should be divided by a factor of two to obtain the con-

centrations relative to the total number of lattice sites.

The approximate solutions that we have derived predict the defect con-

centrations in the form of the Arrhenius relation. This allows us to define so-

called effective formation energies of individual defects as the respective

exponents. For example, Eq. (36) shows that the effective formation energy

of Ni vacancies in stoichiometric NiAl equals e

3. Although the exact solu-

tions of the problem cannot be expressed in a closed form, effective forma-

tion energies of defects can still be derived by fitting the numerical solutions

to the Arrhenius Law in a reasonable temperature range. Since the Arrhenius

Law is not followed exactly, the result may depend on the chosen tempera-

ture range. Even so, the effective formation energies are useful characteris-

tics that reflect basic trends and facilitate a comparison with experiment.

Many of these considerations apply to ionic solids as well. However,

the charge neutrality requirement imposes a new constraint that has to be

incorporated in the statistical-mechanical models of the defects. Besides

vacancies and antisites, many ionics contain interstitials and (almost

inevitably) impurity atoms, as well as electrons and holes.

3.5.3 Effect of Pressure

Until this point, we neglected the pV term in the Gibbs free energy, p

being the external pressure and V the system volume. If the external pres-

sure is high, this term cannot be neglected, and the free energy of defect

formation, Eq. (25), should be written in a more general form:

 e

 Ts

 pV

. (40)

Here, V

is the defect formation volume, which can be defined as the vol-

ume of a relaxed defected block minus the energy of a perfect lattice block

containing the same number of atoms. Furthermore, the free energy of a

composition-conserving defect complex can be expressed in a form simi-

lar to Eq. (40), with the complex volume given by a linear combination of

the respective defect formation volumes. The linear coefficients are iden-

tical to those for the complex energy and entropy.

[79, 86, 87]

For example, the

free energy of a triple defect TA equals:

 e

 Ts

 pV

, (41)

where V

 2V

 V

Ch_03.qxd 11/29/04 6:08 PM Page 137

138 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

Defect complexes whose formation is accompanied by a larger vol-

ume effect are more susceptible to external pressure. Furthermore, the rel-

ative stability of defect complexes at low temperatures now depends on

their enthalpies g  e  pV and not just energies. It is, therefore, con-

ceivable that high pressures can alter the type of the most stable defect

complex. This, in turn, would change the types of constitutional defects.

This scenario is especially plausible for NiAl in which all volume effects

are large due to the significant atomic size difference between Ni and

Al.

[86, 88]

It was predicted that high pressures could change the disorder

mechanism in Al-rich NiAl from the triple-defect type to the antisite type,

and that this change would occur as a first-order isostructural phase

transformation.

[86, 88]

The possible transition between the vacancy-disordered

and antisite-disordered phases of NiAl can be represented by a coexis-

tence line on a p-T phase diagram terminating at a critical point.

Equations (24) and (40) are also valid for point defects in elemental

solids, both in the lattice and in the core of extended defects. The way the

external pressure alters the defect concentration depends on the magnitude

and sign of the defect formation volume. Again, high pressures can affect

the relative importance of defects with different formation volumes,

which in turn can reflect on diffusion rates by different mechanisms.

3.6 Transition Rate Calculations

3.6.1 Transition State Theory

Diffusion in solids is mediated by point defect mechanisms. Under

such mechanisms, point defects walk through the solid by random, ther-

mally activated jumps that displace atoms, thus inducing atomic diffusion.

Each defect jump can induce either a single-atom displacement (for exam-

ple, an atom exchanging with a vacancy) or a collective displacement of

two or more atoms (for example, collective mechanisms on the surface

and in grain boundaries). In most cases, point defect jumps fall under the

category of rare events.

[89]

Namely, the atom moved by a defect makes a

huge number of thermal vibrations around its equilibrium position before

making a successful transition to a new state.

It is convenient to discuss this process by considering a dynamic tra-

jectory of the system on the potential energy surface in its configuration

space. The latter has a dimension, M, varying between 3N and 3N  3

(N being the number of atoms in the system), depending on the boundary

conditions. The initial and final states of the system (i.e., the states before

and after the point defect jump) correspond to local minima on the energy

surface. The two states are separated by an (M  1)-dimensional dividing

Ch_03.qxd 11/29/04 6:08 PM Page 138

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 139

surface that passes along the ridge top between the two energy basins

(Fig. 3.4). We assume that the system follows classical dynamics and is

coupled to a heat bath at a temperature T (canonical ensemble). After

spending a long time wandering within the initial energy basin, the system

eventually accumulates enough thermal energy to reach the dividing sur-

face. Once the dynamic trajectory has crossed the dividing surface, there

is a high probability that it will slide down to the neighboring basin. Once

there, the system will thermalize (establish Boltzmann’s distribution) and

spend a long time in the new state before making another transition back

to the initial or some other state. During the thermalization, the system

forgets how it came to the current state, so that the new jump probabilities

do not depend on the previous jump.

The scenario just described reflects the idea of the transition state the-

ory (TST),

[90]

a powerful tool that enables the calculation of absolute rates,

or rate constants, of thermally activated transitions. The rate constant is

defined as the transition probability per unit time and, in TST, represents

an equilibrium quantity. The critical assumptions of TST are that (1) a

dynamic trajectory crossing the dividing surface inevitably leads to a tran-

sition (i.e., re-crossing events are neglected), and (2) after the transition,

the system has enough time to thermalize before making a next transition.

Other important concepts associated with reaction rate theory are those

of the minimum-energy path (MEP) and the saddle point (Fig. 3.4). The

MEP connects the two energy minima and has the property that the energy

is a minimum in all directions normal to the MEP, but not necessarily along

the MEP. The energy along the MEP reaches a maximum at the saddle

point, which coincides with the intersection of the MEP and the dividing

Saddle point

Dividing surface

(a) Initial Elastic Band

(b) Relaxed Elastic Band

MEP

Figure 3.4 Schematic illustration of the nudged-elastic band method. The lines

show contours of potential energy, 1 and 2 are the initial and final states of a

diffusion jump. The circles mark “images” of the elastic band.

Ch_03.qxd 11/29/04 6:08 PM Page 139

140 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

surface. At the saddle point, one of the eigenvalues of the dynamical matrix

is negative, and the corresponding eigenvector is parallel to the MEP. Thus,

the system at the saddle point has M  1 normal vibration modes. The miss-

ing vibration has converted to a translational degree of freedom associated

with the motion along the reaction path. The importance of the MEPand the

saddle point is that they have the highest statistical weight. Although a par-

ticular dynamic trajectory does not have to coincide exactly with the MEP,

it typically follows it rather closely and crosses the dividing surface near the

saddle point. This makes the saddle point the bottleneck of the transition.

An approximate formulation of TST, called the harmonic TST, is

obtained by applying second order expansions of the potential energy in

the initial state and at the saddle point. Then, the rate constant Γ of the

transition is given by the simple exponential expression:

[91]

Γ  n

exp







. (42)

Here, e

is the energy barrier of the transition, also called the defect

migration energy (hence the superscript m). e

equals the saddle-point

energy minus the initial energy. The pre-exponential factor n

is called the

attempt frequency; it is expressed through normal vibration frequencies of

the system at the saddle point (n

) and in the initial state (n

 .

(43)

This expression originates from the entropy difference between the saddle

point and the initial state evaluated in the harmonic approximation. A

remarkable feature of Eqs. (42) and (43) is that they do not contain any infor-

mation about the final state of the transition. The MEPis not involved either,

except that its direction at the saddle point can be recovered from the eigen-

vector corresponding to the negative eigenvalue of the dynamical matrix.

Equation (42) is the cornerstone of all diffusion rate calculations in

solids. Migration energies of vacancies have been computed for many

elemental solids using either semi-empirical potentials or first-principles

methods. The calculation of n

is a slightly more difficult task, but this has

also been done on many occasions. It is finding the saddle point of the

defect jump that becomes the central problem of the rate constant calcu-

lation in many systems.



i1





M1

i1



Ch_03.qxd 11/29/04 6:08 PM Page 140

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 141

3.6.2 Finding the Saddle Point

For a vacancy jump in a monoatomic crystal, the saddle point can often

be located from symmetry considerations. However, the required symmetry

is not always available. For example, vacancy jumps in a partially disordered

compound are influenced by other point defects residing next to the jumping

vacancy, so that the MEP does not have a symmetry that allows us to locate

the saddle point. Furthermore, self-interstitial jumps in metals are collective

events in which the two atoms forming a split dumbbell move in a concerted

manner to produce the dumbbell rotation with a simultaneous translation of

the center of mass. This process actually involves three atoms moving simul-

taneously, the third one being the atom forming the new dumbbell. As

another example, GB diffusion demonstrates a rich variety of collective

mechanisms mediated either by vacancies or interstitials.

[92, 93]

In these and

other situations, finding the saddle point becomes a challenging problem.

Early diffusion calculations employed the “drag” method, in which

the atom exchanging with a vacancy was moved between its two equi-

librium positions by small steps and the simulation block was partially

relaxed after each step.

[80, 94–97]

The partial relaxation includes arbitrary

displacements of all atoms except for the jumping atom. The latter is only

allowed to move in directions normal to the jump vector (i.e., vector con-

necting the initial and final states). Since no symmetry is imposed on the

MEP, the latter can readily be a curve connecting the two states. The sad-

dle point is identified as the energy maximum along the curve. This

method has proved to work satisfactorily in many applications, including

diffusion in intermetallic compounds and GBs. Aserious limitation of the

method is that only single-atom jumps can be simulated.

More advanced methods of saddle-point search have recently appeared

in the literature.

[98]

Perhaps the most common and best tested of them is the

nudged elastic band (NEB) method, which was successfully applied to a

variety of rate processes in solids.

[98, 99]

To implement the NEB method, the

initial and final states of the transition must be known. The method starts by

generating a number of replicas, or “images,” of the system. The images ini-

tially represent some arbitrary intermediate configurations between the ini-

tial and final states [Fig. 4.4(a)]. For example, they can be created by a lin-

ear interpolation of atomic coordinates. This set of images is referred to as

an elastic band. The total energy of the elastic band is defined as the sum of

actual potential energies of all images plus the sum of fictitious elastic

deformation energies of imaginary springs connecting neighboring images.

This total energy is minimized with respect to atomic displacements in all

images. To improve the convergence, the elastic band is nudged by modi-

fying some components of atomic and spring forces during the energy min-

imization process. Namely, the atomic forces parallel to the elastic band and

Ch_03.qxd 11/29/04 6:08 PM Page 141