Gupta D. (Ed.). Diffusion Processes in Advanced Technological Materials

Подождите немного. Документ загружается.

152 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

transition rate Γ. Knowing all z transition rates, we selected one of them

at random, using the standard KMC procedure (Sec. 3.7.1). The clock is

advanced by the vacancy residence time (the inverse of the sum of all Γs),

and the simulation continues. Thus, the rigid-lattice assumption underly-

ing the standard KMC scheme is replaced by a relaxed lattice at each

vacancy position. More importantly, this scheme does not require a global

rate catalog that attempts to enumerate all possible environments of a

vacancy. Instead, a local catalog is constructed for each vacancy position

and used for making a decision on the next jump. However, as in regular

KMC simulations, the structure and the diffusion mechanism are postu-

lated prior to beginning the simulation.

The computational efficiency of this scheme is poor because the cal-

culation of n

is an extremely demanding procedure. This problem could

be alleviated by using the embedded-cluster method (Sec. 3.4.3), which

restricts the dynamical matrix calculation to a local area around the defect.

Further improvements could be achieved by combining this scheme with

the regular KMC approach. For example, the program could keep in the

memory the structures and local rate catalogs for a number of steps back.

If the vacancy returns to a previously seen configuration, the transition

rates are simply drawn from the memory, not calculated. This can help the

vacancy escape from traps more efficiently by switching to the KMC

mode. Bocquet

[107]

recently proposed a more sophisticated and presum-

ably more efficient detrapping algorithm that guarantees a quick escape of

the vacancy from a pair of sites separated by a low barrier.

A more serious problem, which does not seem to have a solution

within this scheme, is the possibility of unstable vacancy configurations.

Namely, a configuration arising after a vacancy exchange with an atom

can turn out to be mechanically unstable. In that case, the atom would

return to its initial position during the static relaxation. In terms of TST,

the barrier of the return jump is zero or negative, meaning that Vineyard’s

Eq. (42) does not apply. The occurrence of the vacancy instability signals

the existence of a cooperative vacancy jump involving a concerted dis-

placement of two or more atoms. Such unstable vacancies and coopera-

tive vacancy jumps were found in the intermetallic compound NiAl.

[101]

Unstable vacancies were also observed in the simulations of Au-Ni alloys

using this scheme.

[107]

Since the search for alternative diffusion mecha-

nisms is not a part of this scheme, the jumps leading to unstable configu-

rations had to be removed from the catalog, which we hope left the over-

all diffusion process unaffected.

[107]

Henkelman and Jónsson

[103]

proposed a more advanced OFMC

scheme, which they refer to as long-timescale KMC. From each equi-

librium position of the system, possible escape paths are explored by

performing multiple saddle-point searches using the dimer method.

[102]

Ch_03.qxd 11/29/04 6:08 PM Page 152

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 153

Although this procedure can never guarantee that all possible transitions

have been found, the assumption is that the most important transitions

can be identified by a reasonable number of dimer searches. The rele-

vant transition rates are calculated within the harmonic TST. All other

steps are the same as in the regular KMC. In contrast to the previous

scheme, no diffusion mechanism is imposed on the system. The system

is allowed to find the diffusion mechanisms by itself, which can be sin-

gle-atom jumps or collective events of any complexity. Moreover, the

atoms do not even have to occupy lattice positions, which makes the

method suitable for studying amorphous and other structurally disor-

dered systems. This method has been successfully applied to model

metal surface diffusion, island ripening, and surface growth.

[103]

Application to bulk diffusion in alloys and compounds would be an

interesting topic for future research.

3.8 Molecular Dynamics

3.8.1 Calculation of Diffusion Coefficients

Molecular dynamics has been a prime simulation tool in solid-state

diffusion for a few decades.

[146, 147]

In the MD method, the exact dynamic

evolution of a collection of atoms is followed by integrating the

Newtonian equations of motion. The classical forces acting on the atoms

are computed using either interatomic potentials or first-principles meth-

ods. Typically, a canonical ensemble is simulated, in which the system is

coupled to a thermostat under a temperature T. The temperature control is

implemented using the Nose-Hoover method or the Langevin equation

with random forces.

[56]

In most diffusion simulations, the system volume

is held fixed, but it can also be allowed to fluctuate to model constant-

pressure conditions. More sophisticated ensembles, such as the variable

block shape implemented in the Parrinello-Rahman method,

[148, 149]

are

also available but have rarely been applied to diffusion problems.

The most straightforward way of using MD is to calculate the diffu-

sion coefficient from mean-squared displacements of atoms. For a diffu-

sion process mediated by a single type of point defect, the procedure is

very similar to the KMC method (Sec. 3.7.1). Asingle defect is created in

the simulation block, and its random walk is implemented by making a

long MD run. The diffusion coefficient is then deduced from mean-

squared atomic displacements using Eq. (47). The equilibrium defect

concentration c appearing in Eq. (47) should be known from separate cal-

culations. [In some publications, the diffusion coefficient was deduced

directly from Eq. (46) with x  1, which is incorrect.]

Ch_03.qxd 11/29/04 6:08 PM Page 153

154 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

An advantage of this method over KMC simulations is that diffusion

mechanisms do not have to be known in advance. The system evolves nat-

urally under interatomic forces, and the defect has all the freedom to choose

the most favorable diffusion mechanisms. Asignificant drawback, however,

is the limited computational efficiency of MD. Most of the simulation time,

atoms idly vibrate around equilibrium positions without making any contri-

bution to diffusion. Consequently, accumulating good statistics of jumping,

even at high temperatures, is highly problematic. However, estimates of dif-

fusion coefficients of both vacancies and interstitials in metals have been

obtained by this method.

[150]

For diffusion along extended defects, such as

surfaces or GBs, the jump barriers of point defects are lower than in the

bulk, and extensive diffusion can be readily observed already at medium

temperatures. But other problems that come into play are discussed next.

Consider GB diffusion as an example. Due to relatively low transition

barriers of point defects, mean-squared atomic displacements sufficient for

a reliable calculation of the diffusion coefficient can be obtained at tem-

peratures above 0.7T

, where T

is the bulk melting point.

[120, 151, 152]

With

massive parallel computations, the lower bound can be pushed down to

0.6T

[153]

and in the future, it can perhaps be pushed even lower. However,

the energy barriers for the generation of new point defects in GBs are also

relatively low, and generation events inevitably happen during the MD

simulation. The Frenkel pair formation is the most common mechanism of

defect generation, but other mechanisms can also operate, depending on

the GB structure.

[92, 93]

Under such conditions, the number of point defects

in the simulation block is no longer conserved, and the reasoning that led

us to the correction factor x in Eq. (46) no longer applies. One possible

solution could be to perform a very long MD run prior to calculating the

diffusion coefficient, with the hope that the GB would generate the equi-

librium amount of defects. Then Eq. (46) could be applied without any

prefactor. The success of this scheme would depend on the characteristic

time required for the particular GB to arrive at point defect equilibrium. It

can easily be beyond the time scale accessible by MD simulations.

Furthermore, even if the defect generation process is fast enough, the sim-

ple GB structures that are typically simulated do not contain any noncon-

servative sinks or sources of point defects. The total number of atoms in

the GB core is always conserved, meaning that the boundary can only sup-

port an equal number of vacancies and interstitials. This constraint can pre-

vent the GB from ever arriving at the true point defect equilibrium, which

in turn can affect the diffusion coefficient. Optimistically, we can hope that

some of the point defects would migrate away from the GB to the adjacent

lattice regions, bringing the GB closer to equilibrium. However, this migra-

tion also takes time, which again can be beyond the reach of regular MD

simulations. Clearly, this problem needs to be examined carefully.

Ch_03.qxd 11/29/04 6:08 PM Page 154

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 155

3.8.2 Diffusion Mechanisms in Grain Boundaries

Calculating diffusion coefficients is not the only way of using MD

for diffusion. MD also offers an ideal tool for the exploration of unknown

diffusion mechanisms in complex structures. As an illustration, we will

discuss the recent studies of diffusion mechanisms in GBs.

It has been the basic assumption for many years that atoms move in

GBs by simple exchanges with vacancies.

[108, 121, 154]

More recent simula-

tions of GB diffusion in Ag

[116, 152]

and Cu

[93, 114, 115, 155]

pointed to a possible

role of self-interstitials along with vacancies. In the most detailed study of

diffusion mechanisms in GBs,

[92]

diffusion in six symmetrical tilt GBs in

Cu was modeled using an accurate EAM potential

[9]

fit to both experi-

mental data and first-principles calculations. A simulation block contain-

ing about 1200 dynamic atoms was used through the work. Asingle point

defect (vacancy or interstitial) was created at an arbitrary position in the

GB core, and a long MD run was implemented at a constant temperature

of 1000 K. The computer program automatically generated a snapshot of

the block whenever a significant atomic displacement relative to the pre-

viously stored configuration pointed to a possible jump. The diffusion

mechanisms were analyzed a posteriori by examining the whole set of

snapshots produced by the MD run. All snapshots were relaxed in a static

mode, and if two consecutive snapshots were found to relax to different

states, they were assumed to be separated by a defect jump. The relevant

jump barrier and attempt frequency were then determined by the NEB

method (Sec. 3.6.2) by taking the two snapshots as the initial and final

states. These data were later fed into the KMC model for the calculation

of GB diffusion coefficients (Sec. 3.7.2). The NEB calculation also served

to verify that the two states were indeed separated by one saddle point,

which was always found to be the case. Using this laborious but robust

procedure, hundreds of defect jumps were examined and ranked accord-

ing to their rates in a chosen temperature range. The results of this analy-

sis can be summarized as follows.

Vacancies can move in GBs by single-atom exchanges, as they do in

the lattice, but they can also move by collective jumps involving a simul-

taneous displacement of several atoms. Such collective jumps always

involve GB sites that do not support a stable vacancy (Sec. 3.7.2). For

example, site 6 in the Σ  5 (310) GB [Fig. 3.8(a)] is unstable with respect

to vacancy formation: an atom removed from that site is filled by atom 1

during a static relaxation. This instability is responsible for the collective

jump 1→ 6→ 4

∼

of two atoms, as well as for the 1 → 6 → 2

∼

→ 1

∼

jump

involving three atoms. These jumps can be viewed as attempts of vacancy

1 to jump to site 6. Because the latter does not support a stable vacancy, the

vacancy is immediately filled by atom 4

∼

or 2

∼

. As a result, the vacancy jump

Ch_03.qxd 11/29/04 6:08 PM Page 155

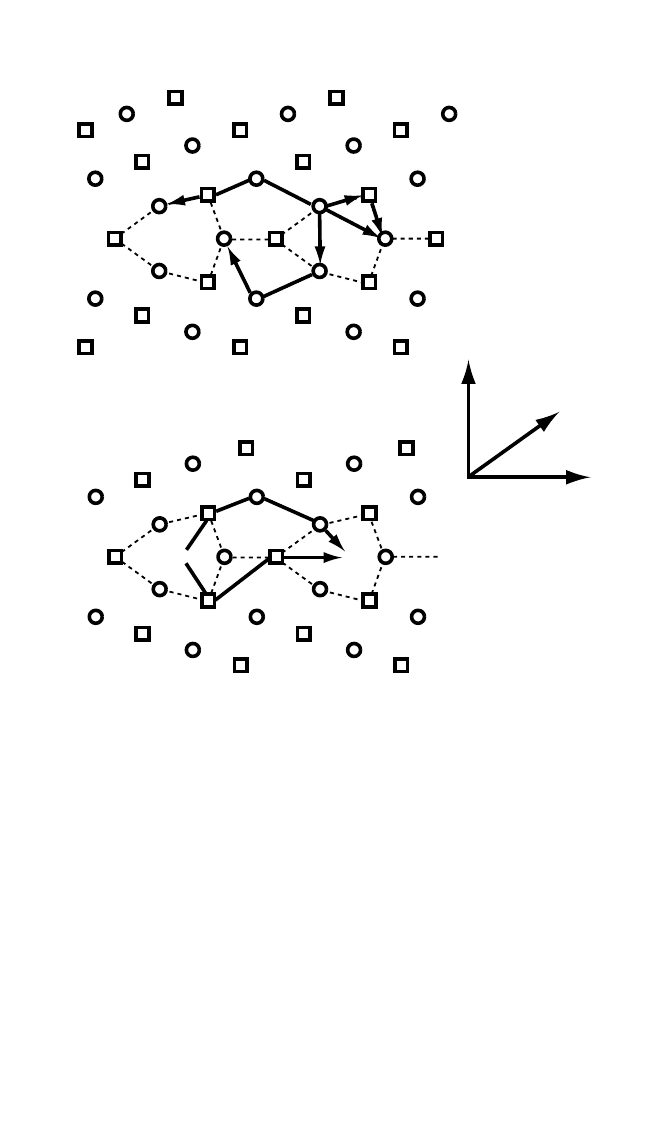
156 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

continues to sites 4

∼

or 2

∼

, without landing at site 6. Collective vacancy

jumps were found to be especially popular in the Σ  7(2 3

∼

1)[111] and Σ 

13(3 4

∼

1)[111] GBs, in which only a few sites support a stable vacancy.

[92]

Interstitials can move by the direct or indirect mechanisms. Under the

direct mechanism, an interstitial atom is wandering along the GB by

jumping between neighboring interstitial positions. While energetically

unfavorable in Σ  5 GBs,

[93]

this mechanism was found to operate in

other GBs.

[92]

Under the indirect mechanism, an interstitial atom displaces

a neighboring regular atom to another interstitial position and takes its

[1 3 0]

[3 1 0]

[0 0 1]

(a) Vacancy Diffusion Mechanism

(b) Interstitial Diffusion Mechanism

Figure 3.8 Vacancy and interstitial diffusion mechanisms in the Σ  5 (310)[001]

grain boundary in Cu.

[92]

Squares and circles mark atomic sites in alternating (002)

planes. Selected sites are labeled for reference. Symbol I labels interstitial posi-

tions.The prime and tilde signs mark symmetrically equivalent sites on either side

of the boundary plane or in neighboring structural units. The arrows show point

defect jumps.

Ch_03.qxd 11/29/04 6:08 PM Page 156

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 157

place. This process occurs by a simultaneous displacement of both atoms.

Furthermore, an interstitial atom can initiate a chain of atomic displace-

ments and push the terminal atom of the chain into an interstitial position,

which can be separated from the initial position. It is important to realize

that all atoms taking part in this process move in concert and not one after

another. Figure 3.8(b) illustrates this mechanism for diffusion perpendi-

cular to the tilt axis in the Σ  5(310)[001] GB. Notice that the same inter-

stitial jump (e.g., I → I

∼

) can be implemented in several different ways,

some of them involving more atoms than others. Interstitial dumbbells in

GBs always move by collective jumps of three or more atoms, as they do

in the lattice. The delocalized crowion-type interstitial configurations

found in the Σ  9 and Σ  11 GBs

[92, 113]

move in a highly collective way

with a very low migration barrier. At each step, individual atoms within

the displacement zone each move by a very small amount but the overall

displacement zone translates by one period along the tilt axis. This motion

looks more like a dislocation glide than an atomic jump.

Besides the vacancy and interstitial mechanisms, ring mechanisms

were also found in GBs. Aring can include up to six atoms and can either

be induced by an existing point defect or happen spontaneously without

any pre-existing defects. On the whole, diffusion in GBs is profoundly

different from lattice diffusion. It occurs by a variety of different mecha-

nisms, most of which are collective. Considering also that the collective

events often happen by a displacement of atomic chains, we can notice an

analogy with diffusion mechanisms in bulk metallic glasses.

3.8.3 Diffusion Mechanisms in Intermetallic

Compounds

Diffusion mechanisms in ordered intermetallic compounds have

been an attractive subject for modeling and simulation for a few

decades.

[34, 106, 156]

(See Chapter 4.) It is generally recognized that diffusion

in such compounds is mediated by vacancies, but the question is, how

exactly do the vacancies move in a structure with long-range order? Aran-

dom vacancy walk would inevitably involve inter-sublattice jumps, which

would soon produce a large amount of antisite defects and eventually

cause a complete disorder of the compound. Vacancies should, therefore,

move in a highly correlated way to preserve the equilibrium degree of

long-range order. Identifying such correlated mechanisms is the key issue

in this area. The simplest possible mechanism is one in which vacancies

migrate on their own sublattices without any inter-sublattice jumps. This

mechanism obviously preserves the crystal order. Alternatively, a number

of cyclic mechanisms have been proposed in which the order is

Ch_03.qxd 11/29/04 6:08 PM Page 157

158 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

destroyed only locally and temporarily and is fully recovered once the

cycle is complete. All mechanisms that have been proposed so far are

based on geometric considerations and have been studied primarily by

KMC simulations within simple models (Sec. 3.7.3). Instead of attempting

to review this whole area, we will focus on recent evaluations of diffusion

mechanisms in the B2-NiAl compound by means of atomistic calculations.

Our aim is to demonstrate the capabilities of atomistic simulations rather

than to make final judgments regarding the role of particular mechanisms.

Similar atomistic calculations of diffusion mechanisms have been performed

for B2-FeAl

[157]

and Ti aluminides TiAl and Ti

Al.

[80]

NiAl is a triple defect compound in which the off-stoichiometry on

the Ni-deficient side is accommodated by structural vacancies on the Ni

sublattice, whereas Ni-rich compositions are dominated by Ni

antisites

[Fig. 3.3(b)]. Given this asymmetry of the disorder mechanism, we should

anticipate an asymmetry and multiplicity of diffusion mechanisms in this

compound. An important feature of the B2 structure is that Ni atoms are

surrounded by Al atoms only and vice versa. Thus, this structure does not

support sublattice diffusion by nearest neighbor jumps. Several diffusion

mechanisms have been proposed for NiAl, including sublattice diffusion

by next-nearest neighbor (NNN) vacancy jumps on the Ni sublattice,

[94, 158]

six-jump vacancy cycles (6JCs),

[97, 159, 160]

the anti-structural bridge (ASB)

mechanism,

[161]

and the triple defect mechanism.

[96, 162]

Some of the mech-

anisms were examined by atomistic computer simulations, with contro-

versial results. For Ni diffusion in NiAl, the lowest activation energy

(2.76 eV in the stoichiometric composition) was found for the NNN

vacancy mechanism, with slightly higher activation energies for the ASB

and 6JC mechanisms.

[94, 163]

It is tempting to conclude that Ni diffuses in

NiAl predominantly by NNN jumps along its own sublattice. However, if

the NNN vacancy mechanism were indeed dominant, this would lead to a

very high Ni diffusivity in Al-rich compositions containing a large amount

of Ni vacancies. This is contrary to the experimental observations by

Frank et al.,

[96]

who found the Ni diffusivity to be about the same in the

stoichiometric and Al-rich compositions. Frank et al. suggested that the

NNN vacancy mechanism is not the dominant one, at least not in the tem-

perature range of their measurements. Instead, they proposed a triple defect

mechanism. The estimated activation energy of the triple defect mecha-

nism (3.18 eV, regardless of the composition) compares reasonably well

with the experimental activation energy in Al-rich and near-stoichiometric

compositions (3.00 ± 0.07 eV), but fails to explain the drop in the exper-

imental activation energy in Ni-rich compositions (53 at.% Ni). Frank

et al. have attributed this drop to a contribution of the ASB mechanism

arising when the concentration of antisites on the Ni sublattice reaches the

percolation threshold.

Ch_03.qxd 11/29/04 6:08 PM Page 158

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 159

Some of these mechanisms have recently been revisited with more

advanced simulation techniques.

[101, 164]

Using an accurate EAM potential,

the migration energy of the NNN jump of a Ni vacancy was found to be

 2.33 eV, a value consistent with concurrent first-principles calcula-

tions.

[101]

This value is low enough to make NNN jumps a plausible diffu-

sion mechanism in NiAl. Since this mechanism presents a standard case

of diffusion on a simple cubic lattice (i.e., Ni sublattice), the activation

energy and pre-exponential factor of diffusion can be readily found, pro-

vided we know the effective formation energy and entropy of Ni vacan-

cies. For the stoichiometric composition, these are given by e

3 and

3, respectively, where e

and s

are the energy and entropy of the

triple defect on the Ni sublattice (Sec. 3.5.2). The values of e

and s

cal-

culated with the same EAM potential are listed in Table 3.1. The resulting

expressions for the Arrhenius parameters are:

 2

13

exp



, (49)

Q e

. (50)

Here, a is the lattice parameter of NiAl, f

 0.653 is the geometric cor-

relation factor for the simple cubic lattice, and n

is the attempt frequency

that was also calculated by Mishin et al.

[101]

Calculations from these equa-

tions give Q  3.09 eV and D

 1.6  10

6

/s, which compare rea-

sonably well with the experimental values Q  3.0 eV and D

 3  10

5

/s.

[96]

This agreement suggests that NNN vacancy jumps in NiAl are

capable of contributing to Ni diffusion significantly and cannot be totally

excluded from the possible mechanisms.

Using static calculation, the 6JC mechanism in NiAl was also eval-

uated.

[101]

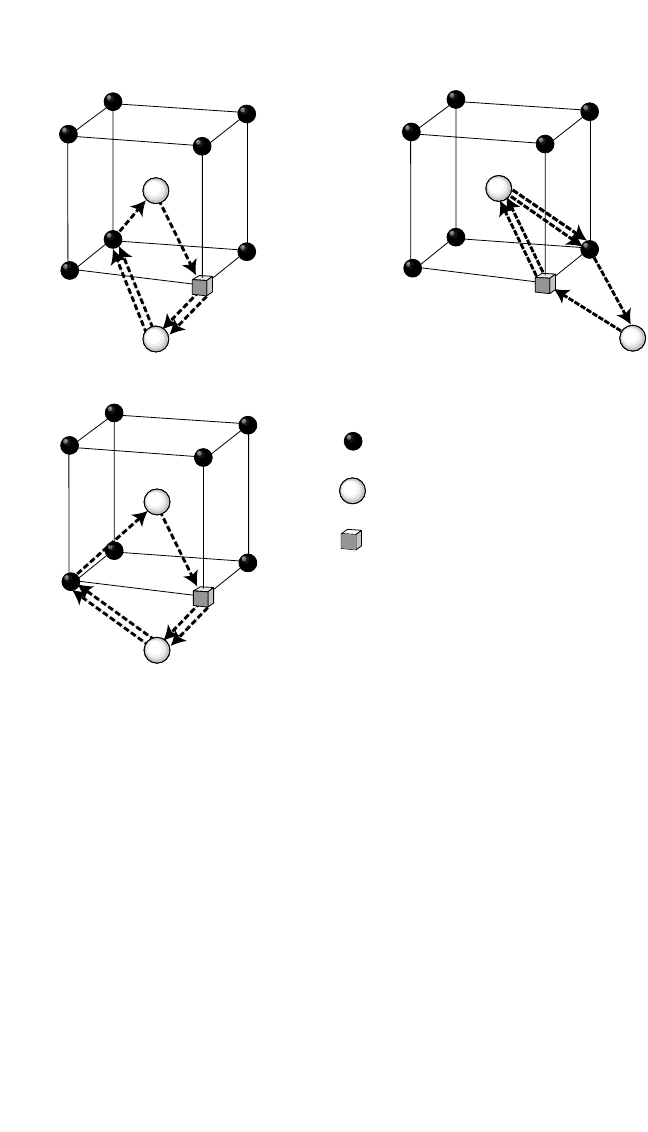
Geometrically, the B2 structure is able to support a [110] cycle

as well as straight and bent [100] cycles (Fig. 3.9). As a result of a cycle,

the Ni vacancy makes a [100] or [110] jump and simultaneously

switches positions of two Al atoms. Each cycle starts with an exchange

of the Ni vacancy with a neighboring Al atom. Calculations have shown

that, contrary to the commonly accepted picture of the 6JC mechanism,

the configuration arising after this first jump is mechanically unstable.

Because of this instability, the vacancy exchanged with an Al atom

returns to its initial position during static relaxation. This important fact

was verified by independent first-principles calculations.

[101]

As we

mentioned before, mechanical instability of a vacancy is always a sign



Ch_03.qxd 11/29/04 6:08 PM Page 159

160 DIFFUSION PROCESSES IN ADVANCED TECHNOLOGICAL MATERIALS

of a collective jump. Indeed, it was found by NEB calculations that the

first jump of a cycle merges with the second one and forms a collective,

two-jump transition.

Three types of such collective jumps are geometrically possible in the

B2 structure, as shown schematically in Fig. 3.6. Jumps 1-2 and 1-2 ini-

tiate [110] and [100] 6JCs, respectively, while jump 1-2 is not involved

in the 6JC mechanism and simply creates two antisites. Due to the inher-

ent symmetry of 6JCs, we can conclude that their last two jumps should

also merge and form collective transitions. Furthermore, NEB calcula-

tions have shown that the central configuration of the [110] cycle is also

mechanically unstable, so that the whole cycle happens as three collective

transitions. For the [100] cycles, the central configuration is stable, and

the cycles happen by two collective transitions separated by two single-

atom jumps. Thus, contrary to the existing paradigm, 6JCs in NiAl happen

Vacancy

(a) [110]

Cycle

(b) [100] Straight

Cycle

Bent Cycle

Figure 3.9 Schematic illustration of six-jump vacancy cycles in the B2 structure of

NiAl.The arrows show vacancy jumps; the numbers label the jump sequence.

Ch_03.qxd 11/29/04 6:08 PM Page 160

ATOMISTIC COMPUTER SIMULATION OF DIFFUSION, MISHIN 161

by either three or four vacancy jumps, not six. This conclusion may have

an impact on future calculations of correlation effects associated with this

mechanism. The collective transitions may also need to be incorporated

into future KMC simulations. NEB calculations also revealed that the

[110] cycle is energetically substantially more favorable than [100]

cycles, suggesting that it is the [110] cycle that should be studied more

carefully in the future.

Diffusion mechanisms in stoichiometric NiAl were also studied by

MD.

[164]

Since the same EAM potential was used, the results could be

directly compared with the static calculations of Mishin et al.

[101]

MD sim-

ulations of NiAl present a serious computational challenge. Due to the

high migration barrier of vacancy jumps (~2.5 eV), the vacancy residence

time is on the order of a nanosecond or longer, even near the melting

point. Consequently, producing even a few hundred vacancy jumps in a

sizable simulation block is already a formidable task for today’s comput-

ers. The simulations were performed at 1900 K (slightly below the exper-

imental melting point) on a 1024-atom simulation block containing a

single vacancy. The vacancy was initially created on a Ni site and was

observed to remain on the Ni sublattice through most of the simulation

time. This observation is consistent with the predominance of Ni vacan-

cies over Al vacancies in this compound [compare Fig. 3.3(b)]. Asnapshot

was saved each time the atomic displacements exceeded a preset critical

value that could signal vacancy jumps. By analyzing the whole set of stat-

ically relaxed snapshots after the MD run, a few hundred sequential

vacancy jumps were found, and their barriers were determined by NEB

calculations. The following diffusion mechanisms were deduced from this

analysis: (1) NNN vacancy jumps on the Ni sublattice; (2) [110] 6JCs

implemented by three collective transitions; and (3) collective [111]

jumps (1-2 in Fig. 3.6). The latter jumps created short-lived configura-

tions that were annihilated by a reverse jump after less than a picosecond.

Such distracting jumps often occurred during the 6JCs but did not change

their course. They also happened very often between NNN jumps or 6JCs.

Collective 1-2 jumps were observed several times but were soon

reversed, and none of them resulted in a complete [100]-type 6JC.

These simulations present what appears to be the first direct observa-

tion of the NNN and 6JC diffusion mechanism in NiAl by MD, along with

a proof of the collective nature of many diffusive events in this compound.

It would be premature to conclude that these two mechanisms totally

dominate diffusion in NiAl. This work did not address other geometrically

possible mechanisms whose simulation would require more than a single

vacancy. For example, to study the triple defect mechanism, two vacan-

cies and an antisite would need to be created in the simulation block.

Although the question of the dominant diffusion mechanism in NiAl

Ch_03.qxd 11/29/04 6:08 PM Page 161