Henini M. Handbook of Self Assembled Semiconductor Nanostructures for Novel devices in Photonics and Electronics

Подождите немного. Документ загружается.

Probing and Controlling the Spin State of Single Magnetic Atoms in an Individual Quantum Dot 449

Another way to reduce the non-radiative losses was to introduce the magnetic atoms in the

quantum dots barriers. This has been realized for CdSe dots embedded in ZnMnSe barriers by

Seufert et al . [18] . In this system, the interaction between the conﬁ ned exciton and the magnetic

ions is due to the spread of the wave function in the barriers and to a small diffusion of the mag-

netic atoms in the quantum dots. In these diluted magnetic semiconductor (DMS) structures, the

response time of the paramagnetic Mn spin was extracted from the transient spectral shift of the

photoluminescence caused by the dynamical spin alignment of magnetic ions incorporated into

the crystal matrix. The formation of a ferromagnetically aligned spin complex was demonstrated

to be surprisingly stable as compared to bulk magnetic polaron [19, 20] , even at elevated temper-

ature and high magnetic ﬁ elds. The photoluminescence of a single electron–hole pair conﬁ ned

in one magnetic QD, which sensitively depends on the alignment of the magnetic ions spins,

allowed measurement of the statistical ﬂ uctuation of the magnetization on the nanometre scale.

Quantitative access to statistical magnetic ﬂ uctuations was obtained by analysing the linewidth

broadening of the single dot emission. This all-optical technique allowed a magnetic moment of

about 100 μ

to be addressed and changes in the order of a few μ

[21–23] to be resolved.

A huge effort has also been done to incorporate magnetic ions in chemically synthesized II–VI

nanocrystals [24] . The incorporation of the magnetic impurities is strongly dependent on the

growth conditions and controlled by the adsorption of impurities on the nanocrystal surface

during growth [25] . The doping of nanocrystals with magnetic impurities also leads to interest-

ing magneto-optical properties [26] but once again, in these highly conﬁ ned systems, the trans-

fer of conﬁ ned carriers to the Mn electronic levels strongly reduces their quantum efﬁ ciency

and prevents the optical study of individual Mn-doped nanocrystals. However, by looking to

MCD absorption spectra it is possible to observe a giant excitonic Zeeman splitting and to deduce

directly the sp–d exchange interaction [27] .

CdTe/ZnTe self-assembled QDs usually present an emission energy below the internal transi-

tion of the Mn atom. The incorporation of magnetic atoms is then possible without losing the

good optical properties of these QDs. Up to now, however, all the experimental studies on these

diluted magnetic QDs were focused on the interaction of a single carrier spin with its paramag-

netic environment (large number of magnetic atoms) [28] . We will see that CdTe/ZnTe quantum

dot structures doped with a low density of Mn atoms allow the optical control of spin states of a

single magnetic ion interacting with a single electron–hole pair or a single carrier.

14.2 II–VI diluted magnetic semiconductors quantum dots

14.2.1 Carrier–Mn coupling

Carrier–Mn coupling was mostly studied in bulk DMS made of II–VI semiconductors in which

Mn impurities were introduced (see the review papers [29, 30] ). These semiconductors are

formed with a cation from column II (Zn, Cd or Hg) and an anion from column VI (Te, Se, S and

more recently even O). These compounds assume the zinc-blende structure or, for the most ionic

ones, the closely related wurtzite structure. Manganese impurities have the d

electronic conﬁ g-

uration and substitute the cations up to 100%. An important point is that Mn substitutes the

column II cation as an isoelectronic impurity – by contrast to the acceptor character observed

in GaAs and similar III–Vs [31, 32] . The Mn ground state is 6S (or 6A1 in cubic or hexagonal

symmetry), introducing localized, isotropic spins with S  5/2. If not interacting, these localized

spins follow Maxwell–Boltzmann statistics, resulting in a magnetization M induced by an applied

ﬁ eld H at temperature T given by a Brillouin function of H / T :

MxNg B

Mn B



052

()

μμ

⎛

⎝

⎜

⎞

⎠

⎟

(14.1)

where x is the proportion of cations substituted by Mn, N

the density of cations in the zinc-

blende or wurtzite structure, g

(Mn)

 2 (to a good approximation) is the Mn Lande factor, μ

is the

CH014-I046325.indd 449CH014-I046325.indd 449 6/27/2008 4:29:47 PM6/27/2008 4:29:47 PM

450 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

Bohr magneton, and k

the Boltzmann constant. This would apply for non-interacting spins. In

the actual material, antiferromagnetic “ superexchange ” interactions appear as soon as the Mn

density is not vanishingly small. These interactions result in a reduction of the magnetization:

this is quantitatively described by using a “ modiﬁ ed Brillouin function ” where x is replaced by

a number of free spins x

eff

, and the argument is H /( T  T

). The values of the two phenomeno-

logical parameters x

eff

and T

are experimentally well documented in the most usual DMSs, such

as Cd

Te [33] . The number of free spins has a direct physical meaning: nearest-neighbour

Mn pairs are blocked antiparallel by the strong superexchange interaction – it can be calculated

from statistics over Mn pairs and clusters either in the homogeneous material [34, 35] , or even at

an interface with the non-magnetic semiconductor [36] . The description by a modiﬁ ed Brillouin

function has proven to be very efﬁ cient at moderately low temperatures (1 to 30 K), moderate

ﬁ eld (up to 5 T), and composition up to x  0.2 [33] . A spin glass behaviour appears at higher

Mn contents in this temperature range, and at lower temperature even for a low Mn content. At

higher temperatures or higher ﬁ eld nearest-neighbour pairs are no longer blocked antiparallel.

It was recognized early that the key property of a DMS is the strong coupling between the bands

of the semiconductor (conduction band and, even more strongly, valence band) and the localized

spins. Optical spectroscopy around the band gap reveals the so-called “ giant Zeeman effect ” , with

a spin splitting proportional to the Mn magnetization [37] . Several studies have demonstrated

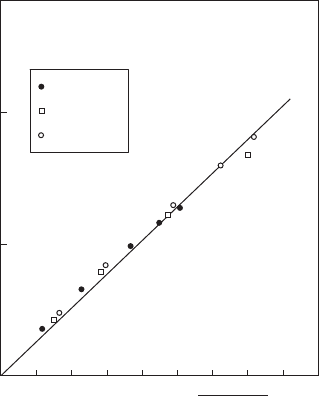
this proportionality and measured the strength of the coupling [38] (see Fig. 14.1 ).

100

1x

E (meV)

0.0 0.05

x  0.031

x  0.071

x  0.095

9 μ

mZnMnTe

Figure 14.1 Splitting of the free exciton line. The straight line is the theoretical dependence calculated for

( α – β )  1.29 eV (from A. Twardowski et al. , Solid State Com., 50 , 509 (1984)).

As a result, magneto-optical spectroscopy is now a very sensitive method for measuring locally

the magnetization of the Mn system. For example, it was applied [33] to measure the diffusion

of Mn across a (Cd,Mn)Te–CdTe interface during the growth by molecular beam epitaxy (MBE).

Actually, the method is quite direct in semiconductors with intermediate values of the band gap

width (tellurides, selenides). In wide band gap semiconductors, ex-citonic effects are important

so that the splitting directly measured on the spectra is not proportional to the spin splitting of

the bands [39] . Altogether, this excellent knowledge of the magnetic properties in (electrically)

undoped II–VI DMSs, and of the coupling between the localized spins and the conduction/

valence band, constitutes a very ﬁ rm basis for the further studies described below.

CH014-I046325.indd 450CH014-I046325.indd 450 6/27/2008 4:29:47 PM6/27/2008 4:29:47 PM

Probing and Controlling the Spin State of Single Magnetic Atoms in an Individual Quantum Dot 451

14.2.2 CdTe:Mn/ZnTe quantum dots

The CdTe/ZnTe QDs samples used in this study are grown by atomic layer epitaxy (ALE) with a

deposition of six monolayers of CdTe on a ZnTe buffer. One should note that the vapour pressure

above the column II or column VI elements in an ultra-vacuum chamber is much higher than

above their compounds. As a result, stable surfaces are obtained under a ﬂ ux of either the cation

or the anion species – another difference with the III–Vs. That implies that (ALE) is feasible [40] ,

as well as MBE under both cation-rich and anion-rich conditions. Cation-rich MBE growth on

a (001) surface proceeds in a 2D mode (layer by layer) up to a sharply deﬁ ned critical thickness

[41] which depends on the lattice mismatch and which corresponds to a plastic relaxation. As

far as the II–VI (QDs) are concerned, the ﬁ rst works published for CdSe QDs in ZnSe [42] and

for CdTe in ZnTe [43] evidence zero-dimensional excitonic properties but did not reported in situ

direct evidence of a spontaneous 2D–3D growth transition (the so-called Stranski–Krastanov

mode). A modiﬁ ed procedure, which involves the re-evaporation of an amorphous layer of the

anion, was developed later [44] , in order to observe in situ a clear 2D–3D transition and to get

well-formed CdTe QDs [45] , and CdSe QDs [46] . With this process, the 2D–3D transition is mainly

induced by a surface energy variation and is revealed by a clear, spotty, reﬂ ection, high-energy

electron diffraction pattern [45, 47] .

Let us explain now how we optimize the growth process in order to get one single Mn into

the QD. Our criterion for the occurrence of such conﬁ guration is a special feature observed in

the photoluminescence (PL) spectra: six narrow lines appear (see below). This corresponds to the

interaction between an exciton with a hole quantized along the growth axis z and a single Mn

ion, whose spin has six projections along this axis [4] . This is the proof that only one Mn inter-

acts with the exciton. When more Mn ions interact with the exciton conﬁ ned in the QD, only

broad lines appear due to statistical magnetic ﬂ uctuations of all the spins of the Mn ions present

in the QD [23, 48] .

A simple geometric modellization shows that if we optimize the Mn density as compared to the

QD one, we could get almost half of all the QDs that contain only one Mn. On a surface with only

one Mn ion and one QD, the probability to have this Mn ion into the QD is a  S

 d

, where

is the QD density and S

is the area of a QD. With different numbers of QDs and Mn ions,

N and p , respectively, this probability becomes p ( a / N )(1  a / N )

 1

. This probability is based on

a random distribution of both QDs and Mn ions and does not assume any correlation between

the QD nucleation and the presence of Mn ions. Then we found that the maximum probability

of QDs having only one Mn is always about 40%, whatever the QD size, for an appropriate Mn

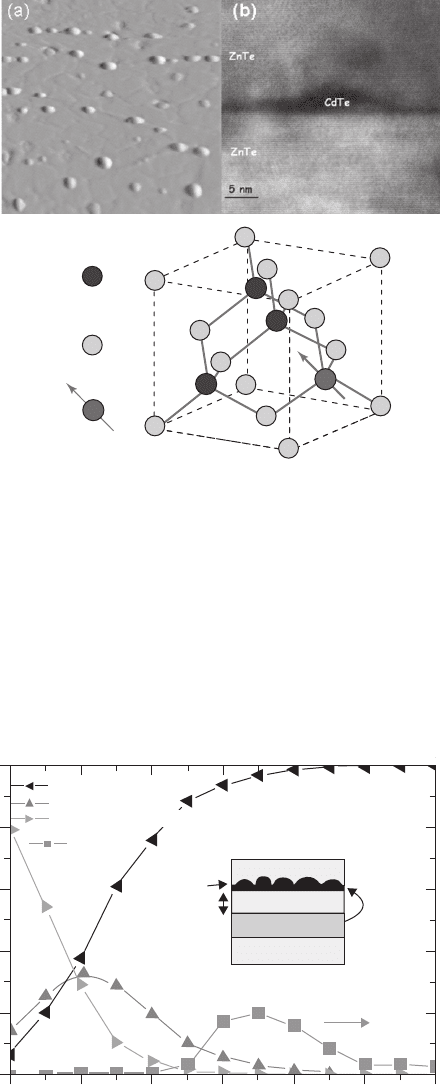
density. This model was applied with the parameters of our CdTe QDs. Atomic force microscopy

gives a density of about d

 3  1 0

QDs/cm

( Fig. 14.2a ). The size and shape of our QDs are

deduced from high-resolution transmission electron microscopy images. QDs are lens shaped

with a typical radius of 5 nm and height of 3 nm ( Fig. 14.2a ). Thus the parameter a is found to be

around 0.02. To go one step further, a single Mn is detected with six well-separated lines if the Mn

ion is near the centre of the QD and also if all the other Mn ions are not in the vicinity of this QD.

The inﬂ uence of these other Mn ions was calculated in [49] . Taking into account such additional

conditions induces a strong reduction of the maximum probability to get only one Mn into the QD

and also reduces the number of Mn ions needed to get this maximum to a very low value [55] .

From this simulation, a concentration of Mn as low as 0.02% is needed for the optimal proba-

bility ( d

/ d

 4). Such an Mn concentration corresponds to an Mn ﬂ ux too low to be controlled

precisely. Thus a speciﬁ c approach to get a very precise composition of Mn over the ZnTe surface

is needed. After a ZnTe buffer growth in order to get a ﬂ at 2D surface, a thin Zn

0.94

0.06

Te buffer

is grown. The Mn composition in this buffer is high enough to be determined very precisely with

reﬂ ection high-energy electron diffraction oscillation calibration [50] . Then a ZnTe spacer of few

monolayers is grown. Segregation of Mn ions into this spacer allows the control of the Mn density

with the number of spacer monolayers. Magneto-optical spectroscopy experiments [36] showed

that every additional monolayer has half the Mn composition of the former one. This model of

interface is currently used to describe segregation at the growing interface [51] . Then the 2D

growth control of the ZnTe spacer layer with a 1 ML accuracy allows us to adjust exactly the Mn

concentration in the QD plane. We have performed a simulation assuming that Mn ions and QDs

CH014-I046325.indd 451CH014-I046325.indd 451 6/27/2008 4:29:47 PM6/27/2008 4:29:47 PM

452 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

are randomly distributed over the surface (in plane) and that Mn ions segregate into the ZnTe

spacer (growth direction). For every carrier in the QDs, the value of the interaction between Mn

ions and the electron (hole) conﬁ ned in the QD is calculated using the wave function as described

later. If these interactions are such that the energy spacing between two successive emission lines

is larger than the spectral resolution of our optical spectroscopy set-up (50 μ eV), a single Mn ion

is present in the dot and can be detected with a comb of six lines. The maximum probability is

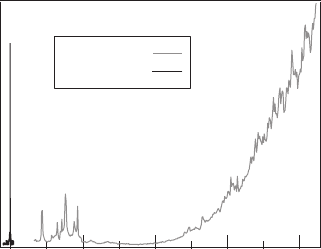
reached when there are four spacer monolayers as shown in Fig. 14.3 (triangle). However, PL

(c)

Figure 14.2 (a) AFM image of a CdTe surface deposited on a ZnTe substrate before deposition of a ZnTe capping

layer. (b) High resolution TEM image showing the structure of a CdTe/ZnTe quantum dot. (c) Crystallin structure of

CdTe with the substitution of a Cd atom by a magnetic Mn atom.

1.0

0.8

0.4

0.6

0.2

0.0

2468

12 14

0.00

0.02

0.04

Probability of QD with only one Mn detectable

0.06

ZnTe

0 Mn

1 single Mn

CdTe QDs

ZnMnTe

ZnTe spacer

ZnTe capping

0.08

0.10

Mn ions

segregation

h: number of spacer MLs

Probability of QD with Mn

Many Mns (2)

1 Mn

detectable

Figure 14.3 Random simulation of the incorporation of Mn ions into the dot as a function of the number of spacer

monolayers. The maximum of single Mn QDs is reached (square) around 9 ML. The inset is a sample cross-section

proﬁ le.

CH014-I046325.indd 452CH014-I046325.indd 452 6/27/2008 4:29:47 PM6/27/2008 4:29:47 PM

Probing and Controlling the Spin State of Single Magnetic Atoms in an Individual Quantum Dot 453

lines are detected only if no other Mn is close to the QD, i.e. if the interaction between all other

Mn and the exciton does not induce an energy spacing above 20 μ eV. With this additional condi-

tion the optimal probability to detect one single Mn ion is reached for a spacer thickness of 9 ML

(square on Fig. 14.3 ). Moreover, this probability is now very low (see the right scale on Fig. 14.3 )

which shows the limit of random incorporation of Mn ions. Such results guide us efﬁ ciently in our

approach to grow QDs doped with a single Mn ion.

14.3 Optical probing of the spin state of a single magnetic atom in a QD

14.3.1 Conﬁ ned carriers–Mn exchange interaction

Microspectroscopy was used to study the magneto-optical properties of individual CdTe/ZnTe

QDs. The low temperature (5 K) photoluminescence (PL) of single QDs is excited with the

514.5 nm line of an argon laser or a tunable dye laser and collected through a large numerical-

aperture objective and aluminium shadow masks with 0.5–1.0 m apertures. The experiments are

carried out in the backward geometry with the propagation direction of the incident and emitted

light parallel to the [001] growth axis. Superconductive coils are used to apply a magnetic ﬁ eld

up to 11 T in Voigt or Faraday conﬁ guration. The PL is then dispersed by a 2 m double monochro-

mator and detected by a nitrogen-cooled Si charged-coupled device camera or an Si avalanche

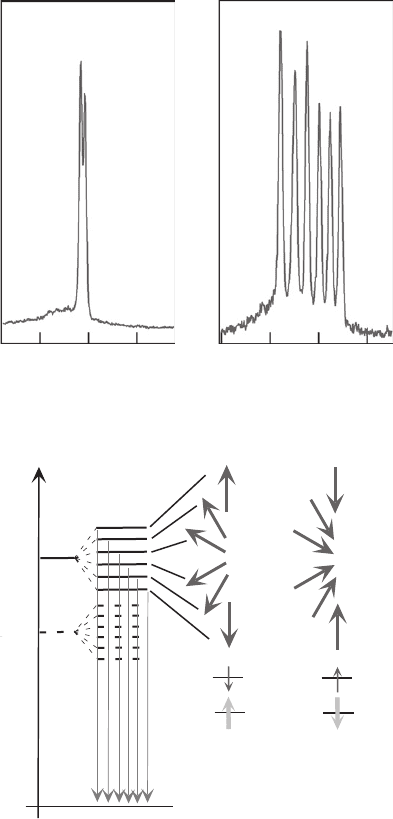
photodiode. Typical photoluminescence and excitation spectra of an exciton in a single CdTe/

ZnTe QD are shown on Fig. 14.4 .

PL intensity (arb. units)

21202080204020001960

Energy (meV)

Exciton PLE

Exciton PL

Figure. 14.4 Photoluminescence and photoluminescence excitation spectra of an exciton in a single CdTe/ZnTe

quantum dot.

In Fig. 14.5 , PL spectra of an individual Mn-doped QD are compared to those of a non-magnetic

CdTe/ZnTe reference sample. In non-magnetic samples, narrow PL peaks (limited by the spec-

trometer resolution of about 50 μ eV) can be resolved, each attributed to the recombination of a

single electron–hole pair in a single QD. The emission of neutral QDs is split by the e–h exchange

interaction and usually a linearly polarized doublet is observed [56] . On the other hand, most

of the individual emission peaks of magnetic single QDs are characterized by a rather large line-

width of about 0.5 meV. For some of these QDs, a ﬁ ne structure can be resolved and six emis-

sion lines are clearly observed at zero magnetic ﬁ eld. The measured splitting changes from dot to

dot. This ﬁ ne structure splitting as well as the broadening is obviously related to the inﬂ uence of

the magnetic ions located within the spatial extent of the exciton wave function. The broadening

observed in magnetic QDs has been attributed by Bacher et al. to the magnetic ﬂ uctuations of the

spin projection of a large number of Mn spins interacting with the conﬁ ned exciton [23] . In the

low concentration Mn-doped samples, the observation of a ﬁ ne structure shows that the QD exci-

ton interacts with a single Mn spin. In time-averaged experiments, the statistical ﬂ uctuations of a

CH014-I046325.indd 453CH014-I046325.indd 453 6/27/2008 4:29:48 PM6/27/2008 4:29:48 PM

454 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

single Mn spin ( S  5/2) can be described in terms of populations of its six spin states quantized

along the direction normal to the QD plane. The exchange interaction of the conﬁ ned exciton

with the Mn atom shifts its energy depending on the Mn spin projection, resulting in the observa-

tion of six emission lines.

QDs doped with single Mn atoms were considered theoretically in the case of spherical nano-

crystals with a strong conﬁ nement [26] . The eigenstates resulting from the exchange coupling

between the exciton and the magnetic ion were obtained by a combination of the electron, hole

and Mn magnetic moments. In ﬂ at self-assembled QDs with a relatively weak conﬁ nement, the

bi-axial strains in the plane of the QD lift the degeneracy of the hole spin projections (heavy-hole/

light-hole splitting). In a ﬁ rst approximation, this system can be described by a heavy-hole

(a)

2098 2099 2100

Energy (meV)

PL intensity (arb. units)

2085 2086

2087

2088

Energy (meV)

PL intensity (arb. units)

(b)

 1

 2

X  MnX

 1 J

 1

5/2

3/2

1/2

1/2

3/2

5/2

3/2

1/2

1/2

3/2

5/2

(c)

Figure 14.5 Low temperature ( T  5 K) PL spectra obtained at B  0 T for an individual CdTe/ZnTe QD (a) and

a Mn-doped QD (b). (c) Scheme of the energy levels of the Mn–exciton coupled system at zero magnetic ﬁ eld. The

exciton–Mn exchange interaction shifts the energy of the exciton depending on the S

component of the Mn spin

projection.

CH014-I046325.indd 454CH014-I046325.indd 454 6/27/2008 4:29:49 PM6/27/2008 4:29:49 PM

Probing and Controlling the Spin State of Single Magnetic Atoms in an Individual Quantum Dot 455

exciton conﬁ ned in a symmetric QD, in interaction with the six spin projections of the manga-

nese ion [52] . The spin interaction part of the Hamiltonian is given by:

HISIjSIj

int e h eh

 σσ

(14.2)

where I

( I

) is the Mn–electron (–hole) exchange integral, I

the electron–hole exchange interac-

tion and σ ( j , S) the magnetic moment of the electron (hole, Mn). The initial states of the optical

transitions are obtained from the diagonalization of the spin Hamiltonian and Zeeman Hamiltonian

in the subspace of the heavy-hole exciton and Mn spin components   1/2



  3/2



 S



, with

  5/2,  3/2,  1/2. Since the dipolar interaction operator does not affect the Mn d electrons,

the ﬁ nal states involve only the Mn states  S



with the same spin component [4] .

In this framework, at zero magnetic ﬁ eld, the QD emission presents a ﬁ ne structure composed

of six doubly degenerate transitions roughly equally spaced in energy. The lower energy bright

states,   1 / 2



  3 / 2



  5 / 2



and   1 / 2



  3 / 2



  5 / 2



are characterized by an anti-

ferromagnetic coupling between the hole and the Mn atom. The following states are associated

with the Mn spin projections: S

  3 / 2,  1 / 2 until the higher energy states   1 / 2



  3 /



  5 / 2



and   1 / 2



  3 / 2



  5 / 2



corresponding to ferromagnetically coupled hole and

manganese. In this simple model the zero ﬁ eld splitting

Mn e h

II

3()

depends only on the

exchange integrals I

and I

and is thus related to the position of the Mn atom within the exciton

wave function.

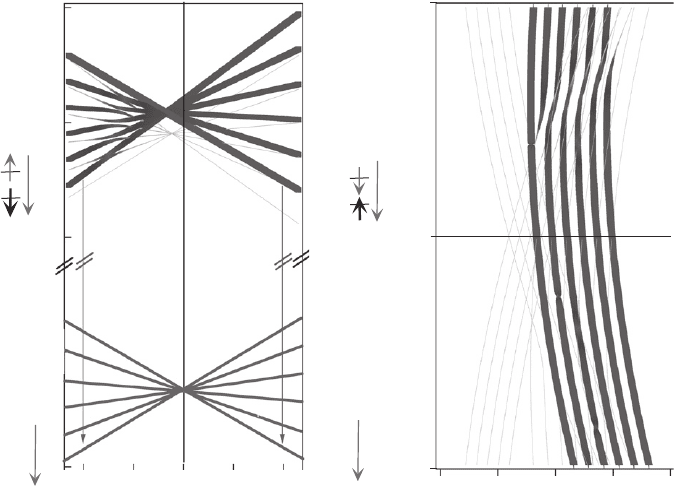
When an external magnetic ﬁ eld is applied in the Faraday geometry ( Fig. 14.6 ), each PL

peak is further split and 12 lines are observed, six in each circular polarization. As presented in

Fig. 14.7 , if the Zeeman effect of the Mn states is identical in the initial and ﬁ nal states of the

optical transitions then the six lines in a given polarization follow the Zeeman and diamagnetic

shift of the exciton, as in a non-magnetic QD. The parallel evolution of six lines is perturbed

around 7 T in σ  polarization by anticrossings observed for ﬁ ve of the lines. In addition, as the

magnetic ﬁ eld increases, one line in each circular polarization increases in intensity and progres-

sively dominates the others.

The electron–Mn part of the interaction Hamiltonian I

( σ  S ) couples the dark ( J

  2) and

bright ( J

  1) heavy-hole exciton states. This coupling corresponds to a simultaneous electron

and Mn spin ﬂ ip changing a bright exciton into a dark exciton. Because of the strain-induced

splitting of light-hole and heavy-hole levels, a similar Mn–hole spin ﬂ ip scattering is not allowed.

The electron–Mn spin ﬂ ip is enhanced as the corresponding levels of bright and dark excitons are

brought into coincidence by the Zeeman effect. An anticrossing is observed around 7 T for ﬁ ve

of the bright states in σ  polarization (experiment: Fig. 14.6 and theory: Fig. 14.7 ). It induces

a transfer of oscillator strength to the dark states. In agreement with the experimental results,

in the calculations the lower energy state in σ  polarization (  1 / 2



  3/2



  5/2)



does not

present any anticrossing. In this spin conﬁ guration, both the electron and the Mn atom have

maximum spin projection and a spin ﬂ ip is not possible.

The minimum energy splitting at the anticrossing is directly related to the electron–Mn

exchange integral I

. For instance, the splitting measured for the higher energy line in σ  polari-

zation ( Fig. 14.6 ), Δ E  1 5 0 μ eV gives I

 7 0 μ eV. From the overall splitting measured at zero

ﬁ eld (1.3 meV) and with this value of I

, we obtain I

  150 μ eV. These values are in good

agreement with values estimated from a modelling of the QD conﬁ nement by a square quantum

well in the growth direction and a truncated parabolic potential in the QD plane. With a quan-

tum well thickness L

 3 nm and a Gaussian wave function characterized by an in-plane locali-

zation parameter ξ  5 nm we obtain I

 6 5 μ eV for an Mn atom placed at the centre of the QD.

However, the ratio of the exchange integral, (3 I

)/ I

  6, for the QD presented in Fig. 14.6 ,

does not directly reﬂ ect the ratio of the sp–d exchange constants β / α   4 measured in bulk

CdMnTe alloys [29] . Such deviation likely comes from the difference in the electron–Mn and

hole–Mn overlap expected from the difference in the electron and hole conﬁ nement length but

it could also be due to a change of the exchange parameters induced by the conﬁ nement [57] .

A dispersion of the zero ﬁ eld energy splitting observed from dot to dot is then due to a variation

of the Mn–exciton overlap for different QDs. However, the spin Hamiltonian (2) does not repro-

duce the observed non-uniform zero ﬁ eld splitting between consecutive lines ( Fig. 14.5b ). As we

CH014-I046325.indd 455CH014-I046325.indd 455 6/27/2008 4:29:49 PM6/27/2008 4:29:49 PM

456 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

will see in the following, a more accurate model has to take into account the full valence band

structure and the heavy-hole/light-hole mixing.

14.3.2 The exciton as a probe of the Mn spin state

As illustrated in Fig. 14.6 , the relative intensities of the six emission lines observed in each cir-

cular polarization depends strongly on the applied magnetic ﬁ eld. The emission intensity, which

is almost equally distributed over the six emission lines at zero ﬁ eld, is concentrated on the high

203920382037

Energy (meV)

σ−

σ+

203920382037

Energy (meV)

2039.52037.5

Energy (meV)

σ

11 T

203920382037

Energy (meV)

11 T

σ−

11 T

Figure 14.6 Magnetic ﬁ eld dependence of the emission of an Mn-doped QD recorded in σ  and σ  polarization.

Anticrossing of the bright and dark states appears around 7 T in σ  polarization.

CH014-I046325.indd 456CH014-I046325.indd 456 6/27/2008 4:29:50 PM6/27/2008 4:29:50 PM

Probing and Controlling the Spin State of Single Magnetic Atoms in an Individual Quantum Dot 457

energy line for the σ  emission and on the low energy line for the σ  emission at high magnetic

ﬁ eld. As the magnetic ﬁ eld increases, the Mn atom is progressively polarized. In time-averaged

experiments, the probability of observing the recombination of the bright excitons coupled with

the S

  5/2 spin projection is then enhanced. Two states dominate the spectra:   1/2



  3 /



  5/2



in the low-energy side of the σ  emission and   1/2



  3 / 2



  5 / 2



in the

high-energy side of the σ  polarization. Changing the temperature of the Mn ion will affect the

distribution of the exciton emission intensities. The PL of the exciton is then a direct probe of

the magnetic state of the Mn ion.

14.3.3 Exciton–Mn thermalization process

The effective temperature of the manganese ion in the presence of the exciton, T

, is found to

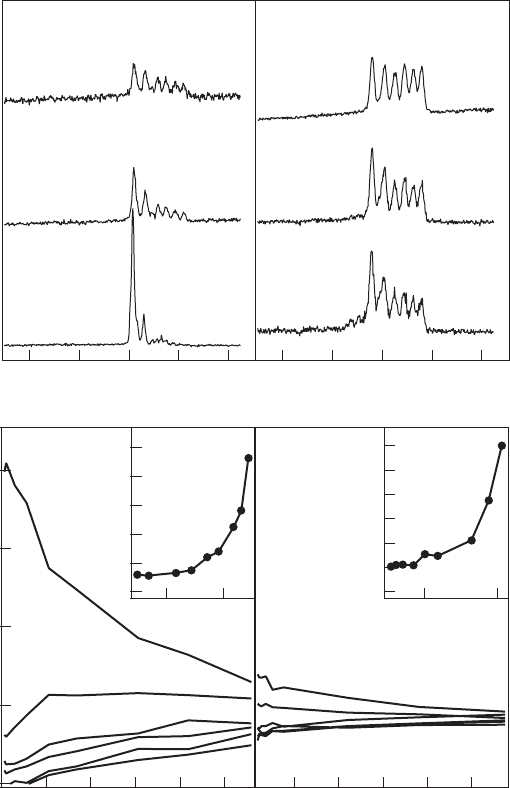
depend of course on the lattice temperature but also on the laser excitation density ( Fig. 14.8 ).

For a ﬁ xed temperature and a ﬁ xed magnetic ﬁ eld, the asymmetry observed in the emission inten-

sity distribution progressively disappears as the excitation intensity is increased ( Fig. 14.8a ). The

variation of T

deduced from the emission rates is presented in the inset of Fig. 14.8c (7 T) and

Fig. 14.8d (0 T) as a function of the excitation density. A similar excitation intensity dependence

of T

was previously observed in DMS quantum wells and was attributed to the heating of the



ions through their spin–spin coupling with the photo-created carriers [58] . The photo-

carriers have excess energy. Via spin–ﬂ ip exchange scattering they pass their energy to the Mn



ions and elevate their spin temperature. The energy ﬂ ux from the Mn to the lattice, determined

by the spin lattice relaxation, will tend to dissipate this excess energy. Under steady-state photo-

excitation, the resulting temperature of the magnetic ions T

exceeds the lattice temperature.

The effect of this spin–spin coupling is strongly enhanced in our system since the isolated Mn



ion is only weakly coupled to the lattice and hardly thermalized with the phonon bath [59] .

(a)

5

0 T

11 T





−

(b)

2 1

Ener

y (meV)





551010

B (T)

Energy (meV)

Figure 14.7 (a) Scheme of the energy levels of the initial and ﬁ nal state involved in the optical transitions of a

quantum dot containing an Mn atom. (b) Modellization of the optical transition obtained from the diagonalization

of an effective spin Hamiltonian including the e–h exchange interaction, the exciton–Mn exchange interaction, the

Zeeman and the diamagnetic energies. The contribution of the dark states appears in green.

CH014-I046325.indd 457CH014-I046325.indd 457 6/27/2008 4:29:51 PM6/27/2008 4:29:51 PM

458 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics

Under non-resonant excitation, the injection of an exciton changes the spin distribution of the

magnetic ion. As illustrated in Fig. 14.8b , at 0 T and at low excitation intensity, an asymmetry

is observed in the emission intensity distribution. This polarization shows that a spin ﬂ ip of the

exciton–Mn system can occur during the lifetime of the exciton. The exchange interaction with

the exciton acts as an effective magnetic ﬁ eld which splits the Mn



levels in zero applied ﬁ eld,

allowing a progressive polarization of its spin distribution.

Resonant excitation of electron–hole pairs directly in the QD limits the exciton–Mn spin relax-

ation [75] . This is illustrated in Fig. 14.9b and c where the emission intensity of the ground state

of an Mn-doped QD is presented as a function of the detection energy when the laser excitation

energy is scanned through the resonant absorption of an excited state identiﬁ ed in a PLE spec-

tra ( Fig 14.9a ). This excitation energy scan reveals that the intensity distribution of the emission

20392038203720362035

Energy (meV)

T  5 K, B  7 T,



150

280

Norm PL intensity (arb. units)

20392038203720362035

Energy (meV)

T  5 K, B  0 T

110

10 100

Exc. Int. (

10080604020

Excitation intensity (

(d)

0.8

0.6

0.4

0.2

0.0

25020015010050

Excitation intensity (

(c)

Emission rate

10 100

Exc. Int. (μW)

(a) (b)

Figure 14.8 (a) Normalized PL (PL spectra divided by the total integrated intensity) in σ  polarization versus

excitation intensity for a ﬁ xed temperature (5 K) and magnetic ﬁ eld (7 T). (b) Excitation intensity dependence of the

zero magnetic ﬁ eld emission of a single Mn-doped QD for a ﬁ xed lattice temperature T  5 K. (c) and (d) Extracted

emission rates of each PL line as a function of the excitation intensity at 7 T (c) and 0 T (d). The inset plots the

extracted Mn effective temperature.

CH014-I046325.indd 458CH014-I046325.indd 458 6/27/2008 4:29:52 PM6/27/2008 4:29:52 PM