Henini M. Handbook of Self Assembled Semiconductor Nanostructures for Novel devices in Photonics and Electronics
Подождите немного. Документ загружается.

Quantum Dot Charge and Spin Memory Devices 489
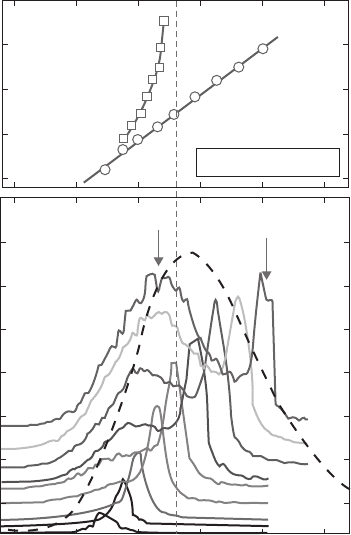
The characteristic form of the charge storage spectra presented in Fig. 15.9a indicated the
existence of two distinct absorption channels: peak R arises from resonant optical charging of
QD ground states while S is due to inelastic charging involving phonons. Following resonant
excitation energy relaxation cannot occur and consequently peak R is observed close to ω
write
(see Fig. 15.9b ). The small 5–7 meV shift observed between ω
write
and R is due to the quantum
confi ned Stark effect, since the electric fi eld differs between charge generation and readout [76] .
The broader, low energy emission band, labelled S , is due to QDs that are quasi-resonantly excited
via their excited state. During this process, photo-generated excitons relax into their ground state
before ionization occurs, resulting in a luminescence band shifted below ω
write
by the energy
separation between ground and excited states. In addition, phonon-assisted excitation may also
contribute to S , due to enhanced exciton–LO-phonon coupling in QDs as evidenced by the barely
resolved satellite features shown in Fig. 15.9 , shifted by Δ E
LO
32 meV below ω
write
. The prin-
cipal mechanisms contributing to S are indicated schematically in Fig. 15.9c and d .
Typical charge storage EL spectra recorded at T 1 0 K and Δ t 1 2 μ s are presented in
Fig. 15.10 (lower panel) as the laser excitation energy is tuned from ω
write
1.370 eV to
1.305
eV. The inhomogeneously broadened PL recorded from the sample under non-resonant
optical excitation is also presented for comparison by the dashed line, revealing a ground state
maximum around 1.340
eV. The positions of peaks R and S are plotted in the upper panel of the
fi gure as a function of ω
write
, showing that R perfectly tracks ω
write
while S saturates close to the
maximum of the inhomogeneously broadened ensemble PL emission. These observations con-
fi rm that peak R arises from single electrons that are optically generated directly into QD ground
states whereafter they do not undergo energy relaxation before readout occurs. In contrast, peak
1.40
1.35
S
R
S
R
T 10 K, Δt 12μs
1.30
1.30
1.35
Ener
g
y (eV)
1.40
EL intensity (arb. units)
Figure 15.10 Typical electron charge storage spectra recorded at T 10 K, Δ t 1 2 μ s as ω
write
is tuned from
1.370 eV (red curve) to 1.305 eV (purple curve). The characteristically sharp peak R arising from resonant charge
generation and readout clearly tracks the laser excitation energy (top panel) while the energy of the broader satellite
peak S saturates around 1.34 eV confi rming its origin as arising from quasi-resonant QD excitation via excited
states. The dashed line shows the inhomogeneously broadened photoluminescence spectrum for comparison.
CH015-I046325.indd 489CH015-I046325.indd 489 6/24/2008 5:06:30 PM6/24/2008 5:06:30 PM
490 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics
S arises from electrons that are quasi-resonantly excited into QD excited states, from where they
undergo energy relaxation into the ground state before readout occurs. The fundamental princi-
ple of wavelength selective optical QD charging proposed in [46] is, thus, demonstrated; the stor-
age EL signal close to peak R corresponding to direct frequency selection of a sub-ensemble of QDs
for electron storage and subsequent voltage triggered readout of the stored charge distribution.
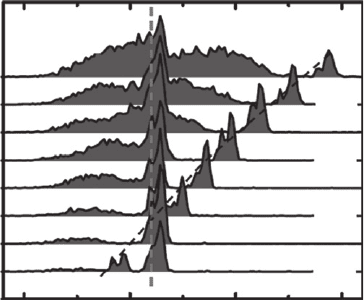
The wavelength selective nature of the experiment can be confi rmed by performing two-colour
experiments, applying a sequence of optical pulses with different frequencies during each excitation
cycle. The fi rst pulse, delivered by a diode laser, was centred at ~1.27 eV while the second pulse
from the Ti–sapphire, at ω
write
, was tuned over the ground state absorption spectrum. Typical
charge storage spectra after Δ t 1 2 μ s are presented in Fig. 15.11 . For both excitation energies
the emission spectrum has the form described above, consisting of a resonant peak R close to
the excitation energies and a weak low energy side band S . In full agreement with the discussion
above, the side band intensity increases as ω
write
is shifted into the region of excited state absorp-
tion. These results demonstrate unambiguously that two separate and distinct sub-ensembles are
charged by the two-excitation frequencies, reaffi rming the conceptual basis for implementation
of wavelength division multiplexing for information storage using inhomogeneously broadened
media such as QDs. It is also remarkable that, for excitation intensities well below saturation, as
is the case for the data presented in Fig. 15.11 , crossing of these energies results in a superposi-
tion of the charge storage signal and no loss of “ information ” .
1.33
4.2 K
V
reset
= 0.6 V
PL intensity
1.30
1.28
1.25
1.351.301.25
Energy (eV)
1.20
Figure 15.11 Demonstration of two colour charge storage experiment following simultaneous excitation with a
laser diode at ~1.26 eV and a tunable pulse from a Ti–sapphire laser.
15.2.3 Thermal redistribution and loss of electrons and holes
Before continuing to discuss the potential to use the present devices to probe spin dynamics and
deduce spin fl ip mechanisms for electrons and holes, we examine the temporal and thermal sta-
bility of the optically generated charge distribution. These measurements demonstrate that car-
riers optically generated directly into QD ground states (peak R ) remain in the dot where they
were generated over ultra-long timescales at low temperatures and are only thermally lost from
the dots at elevated temperatures approaching ~100 K [77] . Analysis of the temperature depend-
ence of the charge storage data yields the activation energy, showing that the wetting layer acts
as the dominant redistribution channel.
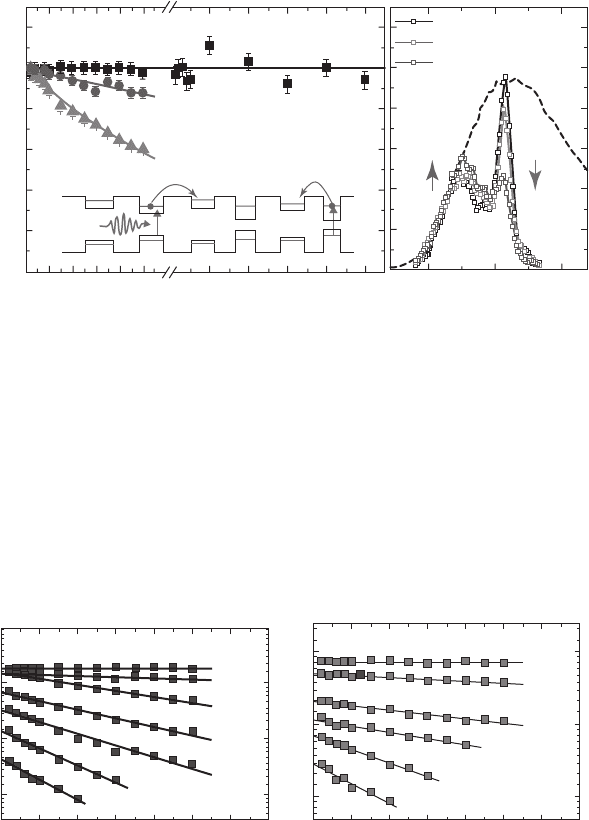
Figure 15.12a shows the intensity of R for an electron storage sample as a function of Δ t ,
recorded at temperatures of 10 K, 90 K and 100 K. At T 10 K, no temporal evolution is observed
indicating that resonantly generated electrons are not thermally activated out of the dots in
which they were created over very long ( 1 ms) timescales. Indeed, evidence for charge dynam-
ics over these timescales could only be observed at much higher temperatures. This behaviour
CH015-I046325.indd 490CH015-I046325.indd 490 6/24/2008 5:06:31 PM6/24/2008 5:06:31 PM
Quantum Dot Charge and Spin Memory Devices 491
is illustrated by the data presented in Fig. 15.12b which compares electron storage spectra
recorded at T 110 K for Δ t 0.2 μ s, 1.0 μ s and 5 μ s. As the storage time increases, a clear
decrease in the intensity of R can be observed as electrons are thermally activated out of the dots
in which they were resonantly generated. This behaviour is accompanied by an anticorrelated
increase of the intensity of S showing that electrons may thermally redistribute throughout the
QD ensemble (as depicted schematically by the inset on Fig. 15.12 ) at suffi ciently high tempera-
tures but, nevertheless, remain stored within the QD ensemble and are not lost. The results pre-
sented in Fig. 15.12 confi rm that for T 50 K, the resonant nature of the charge storage process
is preserved over timescales 1 ms, forming the basis for analysis of electron and hole spin
relaxation dynamics presented later in the chapter.
1.2
1.0
0.8
0.6
τ
store
(90 K) (60 ± 5) μs
τ
store
(10K) >> 1ms
τ
store
(100 K) (30 ± 5) μs
0.4
Normalized peak intensity
0.2
0.0
012345
200
Storage time Δt (μs)
Energy (eV)
0.2 μs
1 μs
5 μs
~110 K
400 600 800 1000 1.25 1.30 1.35
(a)
(b)
SR
hω
in
Figure 15.12 (a) Temporal stability of selectively generated electron distribution. Time decay transients of the
peak R are presented at temperatures of 10 K, 90 K and 100 K demonstrating the complete absence of thermal
charge redistribution via the wetting layer continuum at low lattice temperature. (b) Spectra recorded at 110 K for
Δ t 0.2, 1.0 and 5.0 μ s showing that temporal charge redistribution dynamics are only important at high lattice
temperature; the amplitude of peak R quenching with increasing storage time while peak S becomes stronger.
10 K
10 K
50 K
65 K
70 K
75 K
80 K
90 K
100 K
105 K
110 K
115 k
e
(a) (b)
h
120 k
012
I
R (Δt) (a.u.)
34
Δt (μs) Δt (μs)
567 01234567
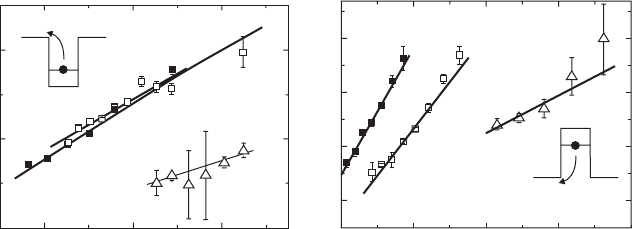
Figure 15.13 Temporal evolution I
R
( Δ t ) of the peak R intensity as a function of storage time Δ t , at increasing
temperatures, for the electron (a) T 10 to 110 K and hole (b) T 10 to 80 K storage devices. The data are repre-
sented on a logarithmic scale. The excitation energy is ω
w
1.272 eV. Grey curves: Single exponential decay fi ts of
I
R
( Δ t ). Data replotted from [77] by permission of the American Physical Society.
To identify the nature of the thermal redistribution channel, the intensity of R was measured
as a function of time ( I
R
( Δ t )) for different lattice temperatures and ω
write
. Typical data are pre-
sented in Fig. 15.13a for an electron storage sample and in Fig. 15.13b for a hole storage sam-
ple with ω
write
1.272 eV, reproduced from [77] . Both electron and hole storage devices exhibit
similar behaviour but over a different temperature range. Over this time range I
R
( Δ t ) remains
constant up to T
c
,
e
90 K for the electron storage device, while for the hole storage device it only
CH015-I046325.indd 491CH015-I046325.indd 491 6/24/2008 5:06:31 PM6/24/2008 5:06:31 PM
492 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics
remains constant up to T
c
,
h
50 K. For T T
c
,
e
(
h
)
the intensity of peak R decays exponentially
with Δ t . Near the critical temperature, the decay time constant τ , as determined by a single expo-
nential decay fi t (grey curves in Fig. 15.13a and b ) is τ 10 μ s, and decreases continuously as
the thermal redistribution channel becomes accessible [77] . These results demonstrate that for
temperatures up to T
c
,
e
(
h
)
no charge redistribution occurs and spectral information is preserved
over microsecond timescales. For higher temperatures, the temporal behaviour of the peak R
intensity as well as the observed excitation energy dependence of the decay times suggests a ther-
mally activated charge redistribution process among the QD ensemble via a high energy channel,
which introduces an important time-dependent mechanism for loss of spectral selectivity in the
QD charging process.
Figure 15.14a and b show an Arrhenius analysis of the fi tted temperature-dependent car-
rier redistribution rate for both electron (a) and hole (b) storage devices for the three different
excitation energies investigated ( ω
write
1.272, 1.298 and 1.342 eV). This analysis is based on
the detailed balance between the QD capture and emission rates at thermal equilibrium, under
the assumption that the QD capture cross-section is temperature independent. In this case, the
QD thermal emission rate τ
1
( T ) can be expressed as τ ( T )
1
AT
3/2
exp (where is a tempera-
ture-independent constant, the Boltzmann constant and the activation energy for the thermally
activated redistribution process [57] . Thus, a plot of ln ( τ versus e / i should yield a straight line
with a slope equal to the activation energy corresponding to the mechanism driving the thermal
redistribution.
100
10
12
14
64 /3 meV
32 /9 meV
57 /4 meV
47 /3 meV
14 /4 meV
35 /3 meV
e
h
120
e/K
B
T(1/eV) e/K
B
T(1/eV)
140 150
9
10
11
12
200 250 300 350
In(τT
2
)
Figure 15.14 Arrhenius analysis of the fi tted charge redistribution rates for electrons (left panel) and holes (right
panel). As discussed in the text, analysis of the measured charge redistribution rates yield activation energies for the
thermally driven redistribution processes.
The results obtained from our analysis are summarized in Table 15.1 . The fi rst column dis-
plays the excitation energy whereas the measured activation energies E
A
,
e
(
h
)
for electrons (e)
and holes (h), respectively, are presented in columns 2 and 3. Activation energies ranging from
E
A
,
e
3 2 9 up to 64 3 meV are obtained for electrons and E
A
,
h
1 4 4 to 47 3 meV for
holes. These values provide information on the single particle energy structure of the conduc-
tion and valence bands, namely the energy difference between the stored particle ground state
and the redistribution channel band edge. As expected, the activation energies decrease as the
excitation energy is increased; smaller activation energies are obtained for holes. The interband
energy of the recombination channel E
ch
can be estimated from these single particle results since
the electron and hole storage devices ’ electronic structures are similar, a concept which is sup-
ported by the similar interband optical properties in emission (PL) and absorption (photocurrent)
spectroscopy. The fourth column of Table 15.1 shows the calculated values of E
ch
, obtained by
summing the single particle activation energies E
A
,
e
(
h
)
and the excitation energy, ω
write
, while
neglecting excitonic effects. Remarkably, E
ch
is found to be almost constant at ~1.390 eV for all
three excitation energies investigated, confi rming that redistribution occurs via the wetting layer.
CH015-I046325.indd 492CH015-I046325.indd 492 6/24/2008 5:06:32 PM6/24/2008 5:06:32 PM

Quantum Dot Charge and Spin Memory Devices 493
Further increase of the sample temperature to values much higher than the critical tempera-
ture results in loss of stored charge from the QD layer over the Al
0.4
Ga
0.6
As blocking barrier. This
effect manifests itself as a temporal decay of the total integrated intensity I
tot
( Δ t ) of the storage
spectra with storage time unlike the temporal redistribution discussed above. For the electron
storage device, I
tot
( Δ t ) was found to be virtually time independent up to T 130 K signifying that
electrons do not escape from the QD layer. At higher temperatures, the escape time constant was
found to be τ
esc
10 μ s at 150 K. Similar results were obtained for the hole storage sample.
To summarize this section, the results discussed have demonstrated effi cient wavelength selec-
tive storage of electrons and holes in InGaAs-GaAs self-assembled QD-based devices and their
optical readout. Furthermore, they show that wavelength domain data storage can be achieved,
with ultra-long charge retention times in excess of milliseconds at T 10 K. Analysis of the form
of the storage spectra revealed the contribution of several absorption mechanisms, such as purely
resonant absorption in the QD ground states, quasi-resonant absorption in the QD excited states
as well as LO-phonon-assisted absorption. The potential for wavelength division multiplexing has
been demonstrated using two-colour experiments, where independent charging of two distinct
sub-ensembles of QDs has been clearly identifi ed. Finally, time resolved measurements were used
to probe post-absorption redistribution of resonantly generated charge among the QD ensemble.
Thermal charge redistribution was shown to be negligible for low temperatures ( T 60 K) and
occur over microsecond timescales at elevated temperatures ( T 100 K). An activation energy
analysis demonstrated that the 2D wetting layer beneath the QDs is the dominant redistribution
channel. We continue in the next section to discuss how these concepts for optical charge genera-
tion can be extended to achieve optical spin generation. The high stability of optically generated
charges allows investigation of spin relaxation dynamics in self-assembled QDs.
15.3 Optical spin orientation
15.3.1 Selection rules for the neutral exciton transition in QDs
To extend the concepts introduced above from optical charge storage to “ spin storage ” a key
consideration is the spin structure of the QD ground state exciton transition. The exciton states
are constructed from electron and heavy-hole * single particle basis states with spin projections
of J
e
,
z
1/2 , or 1/2 (e ↑ or e ↓ ) and J
h
,
z
3/2 , 3/2 (h ↓ and h ↑ ), respectively [78] .
As a result, four exciton states can be formed with total angular momentum projections of
J
X
,
z
S
z
e
J
z
h
1 (e ↓ h ↑ and e ↑ h ↓ ) and 2 (e ↑ h ↑ and e ↓ h ↓ ), respectively. Since a circularly
polarized photon conveys a single unit of angular momentum ( 1 for σ
and 1 for σ
) and
the optical transition takes place to the crystal ground state, only the J
X
,
z
1 (e ↓ h ↑ and e ↑
h ↓ ) states are optically active, the J
X
,
z
2 states remaining dark. As depicted schematically
in Fig. 15.15 , the isotropic electron–hole exchange interaction lifts the degeneracy of these four
states forming a J
X
,
z
1 bright doublet at higher energy, with the J
X
,
z
2 dark states shifted
by δ
0
1 0 0 μ eV to lower energy. These ideas have been broadly confi rmed by single dot spectros-
copy experiments [78, 79] .
Table 15.1 Summary of the activation energy analysis. First column : Excitation
energy ω
write
. Second and third columns : Activation energies E
A
,
e
and E
A
,
h
for
electrons and holes, respectively, obtained using an Arrhenius analysis of the fi t-
ted decay time. Fourth column : Estimated energy E
ch
of the redistribution chan-
nel obtained by summing ω
write
, E
A
,
e
and E
A
,
h
.
1272
64 3 47 3 1393 6
1298
57 4 35 3 1390 7
1342
32 9 14 4 1388 13
* The predominant heavy-hole character of the ground state arises from the large bi-axial compressive strain
present in InGaAs–GaAs QDs.
CH015-I046325.indd 493CH015-I046325.indd 493 6/24/2008 5:06:33 PM6/24/2008 5:06:33 PM
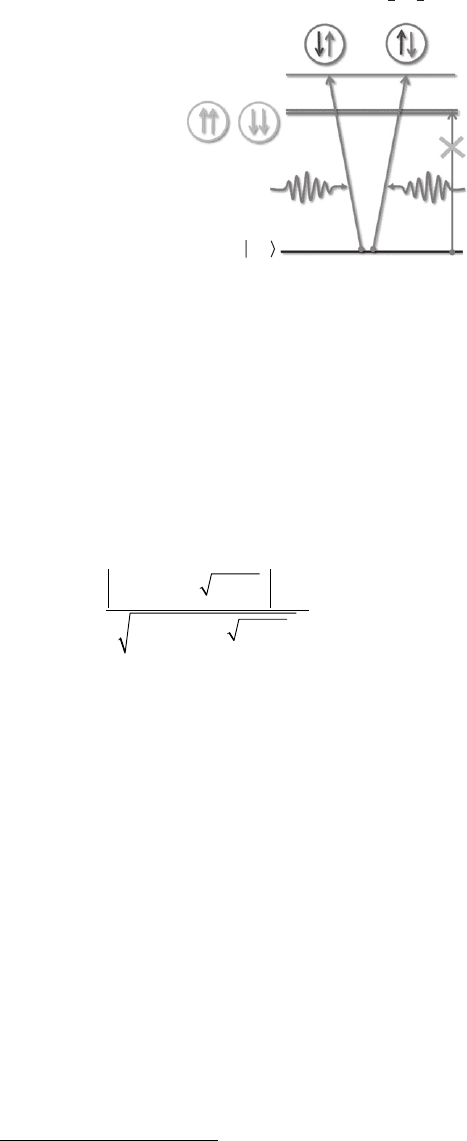
494 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics
The nominally degenerate bright states (e ↑ h ↓ and e ↓ h ↑ ) are generally mixed in dots due to
a reduction of their symmetry. This symmetry reduction is related to the lack of inversion sym-
metry of the underlying zinc-blende crystal structure and possible asymmetries in the effective
confi nement potential due to piezocharges and dot morphology. This results in the formation of
two linearly polarized eigenstates
|L
separated by a few 1 0 μ eV ( δ
1
) in the absence of a static
magnetic fi eld [78, 80] . The general character of these bright exciton eigenstates in a QD subject
to a static magnetic fi eld applied parallel to the QD growth direction can be represented by:
|L
rr
rr r
〉
〉
()
〉
()
111
21 1
2
22
(15.1)
where the parameter r is the ratio of the exciton Zeeman energy to the anisotropic exchange split-
ting ( r g
ex
μ
B
B ). In order to enable optical selection of pure J
X
,
z
1 spin states all the meas-
urements described below were performed with static magnetic fi elds B 4 T applied parallel to
the growth axis of the dots. This results in the formation of pure spin eigenstates provided that
gB
ex B
μ
(i.e. r ) [78] . In this case, excitation with circularly polarized light with σ
or σ
helicity then selectively generates electrons with up (e ↑ ) or down (e ↓ ) spin orientation, respectively,
after the charge storage mechanism is completed. * All the measurements presented in this chap-
ter were recorded in the regime where r and the excitonic states involved are well represented
by Fig. 15.16 . When the charge storage signal is read out after a time delay Δ t , holes with ran-
dom spin orientation are injected into the dots from the back contact forming equal populations
of bright and dark states. Only the bright excitons recombine during the gating time of the sin-
gle photon detector and the degree of circular polarization of the emitted EL (DoP ( I
σ
I
σ
)/
( I
σ
I
σ
)) provides a direct optical probe of the electron spin orientation a time Δ t after optical
initialization.
In order to test these expectations we performed charge storage measurements with circular
polarization discrimination in both excitation and detection channels and large static magnetic
fi elds applied parallel to the QD growth axis. Selected examples of the results of these measure-
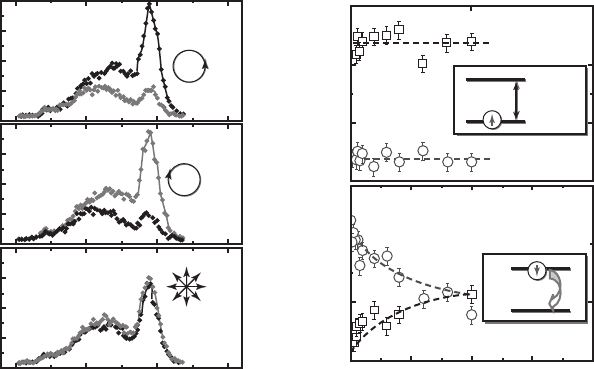
ments recorded at T 1 K, B 8 T and a storage time of Δ t 2 μ s are presented in the upper
two panels of Fig. 15.16a . Storage spectra following excitation with σ
( Fig. 15.16a – upper
panel) and σ
( Fig. 15.16a – middle panel) polarized light were recorded and analysed with σ
J = 0
cgs
J ±2
“dark”
“bright”
σ
σ
J S
e
J
h
z
3
2
1
2
1
Figure 15.15 Schematic representation of the spin fi ne structure of the heavy-hole exciton in a self-assembled
QD. The optically active bright exciton states J 1 can be addressed using circularly polarized light and are spec-
trally split from the dark J 2 states by the isotropic exchange interaction energy. An anisotropic component of
the exchange interaction energy mixes the nominally pure J 1 and 1 eigenstates to produce a pair of linearly
polarized transitions separated by the anisotropic exchange interaction energy.
* This statement assumes that the electron component of the exciton g -factor is negative as is normally the case
for self-assembled quantum dots.
CH015-I046325.indd 494CH015-I046325.indd 494 6/24/2008 5:06:33 PM6/24/2008 5:06:33 PM
Quantum Dot Charge and Spin Memory Devices 495
( σ
) discrimination in the detection channel as shown by the red (black) curves on Fig. 15.16 .
Under these experimental conditions, after spin initialization with circularly polarized light the
storage EL in the vicinity of the resonant peak ( R ) is found to be predominantly co-polarized
with a DoP 65%. This indicates that spin orientation of the optically generated single electrons
is preserved over the Δ t 2 μ s storage time. In contrast, following excitation with randomly
linearly polarized light ( Fig. 15.16a – lower panel) we observe zero degree of circular polariza-
tion demonstrating that spin alignment due to, e.g., inter-Zeeman level thermalization does not
occur over such short storage times. This observation already suggests that the longitudinal spin
relaxation time ( T
1
) is much longer than the 2 μ s storage time investigated in Fig. 15.16 . Here,
we note that the population of the two Zeeman levels can be described by Boltzmann statistics,
i.e.
NN g B kT
ex B B↓↑
/≈exp( ) μ
. F o r T 1 K, we estimate that N
↓
/ N
↑
10
5
demonstrating
that the single electron spins probed should occupy the lower Zeeman level in the system at ther-
mal equilibrium if thermalization were fast compared with Δ t .
The results presented in Fig. 15.16a demonstrate clearly that the storage signal exhibits a pro-
nounced polarization memory effect for both spin orientations (excitation helicities). This arises
from the reversible transfer from optical polarization to electron spin orientation followed by
electron spin storage for a time Δ t 2 μ s and back-transfer from electron spin orientation into
optical polarization. Analysis of the dynamics of the optical polarization provides direct informa-
tion about the timescales for spin relaxation in self-assembled QDs as discussed later on. However,
before discussing investigations of spin relaxation dynamics we review some of the fundamental
mechanisms for spin relaxation in semiconductor nanostructures.
15.3.2 Spin relaxation in semiconductor nanostructures
Spin fl ip relaxation in bulk III–V semiconductor materials is primarily due to scattering processes
that can couple to the spin of the electron via the spin orbit interaction (SOI). Coupling of the spin
1200 1250 1300 1350
σ
σ
σ
σ
σ
σ
σ
σ
(b)
(a)
300
EL intensity (arb. units)
200
100
0
200
100
0
0 500 1000
Storage time (μs)
Energy (meV)
1500 2000
σ
σ
gμ
B
B
Figure 15.16 (a) Charge storage spectra recorded with circular polarization discrimination in the excitation
and detection channels at B 8 T and T 1 K (upper panel σ
excitation, middle panel σ
excitation, lower
panel linearly polarized excitation). (b) Intensity of storage luminescence recorded with circular polarization dis-
crimination of both the excitation and detection channel. The upper panel shows the result of optically pumping spins
into the lowest Zeeman level. No time evolution is observed since the system is prepared in a state close to thermal
equilibrium. In contrast, pumping spins into the upper Zeeman level reveals a clear time evolution (lower panel), from
which the spin–fl ip lifetime is measured. Data redrawn with permission from [75] .
CH015-I046325.indd 495CH015-I046325.indd 495 6/24/2008 5:06:33 PM6/24/2008 5:06:33 PM

496 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics
to the orbital motion is well known in atoms to have relativistic origins, arising from the interac-
tion of the electron spin with an effective magnetic fi eld experienced by the electron as it moves
in the electric fi eld of the nucleus. Quite generally, an electron moving with momentum in a vac-
uum experiences an effective magnetic fi eld
BEprr
eff
()/2
, the origin of which can easily be
appreciated by visualizing the electron in its rest frame whereupon the positively charged nucleus
executes orbital motion around it, generating a magnetic fi eld at the position of the electron. In
semiconductors, SOI will result in the electron spin precessing in
B
as
as it propagates with a
momentum
p
through the material. The direction of and
E
will be constant during unin-
terrupted ballistic motion but change upon scattering from phonons, impurities or other charge
carriers. As a result, the randomization of the electron’s momentum by scattering will be accom-
panied by a scrambling of its spin orientation. Rather surprisingly the angle through its spin
as it is rotated while it executes ballistic motion turns out to be independent of the velocity
vp
.
This rather surprising result is a consequence of the fact that the precession frequency of the
spin depends on
|B
that itself is determined by
vp
. Thus, if an electron moves with a larger
velocity it also precesses faster and the net rotation over a given path length is the same. As a
result, the strength of the SOI in any material can generally be characterized by the distance
over which an electron must travel before its spin rotates by an angle π . This length is termed the
spin–orbit length and is typically of the order of ᐍ
SO
1–10 μ m in Ga(In)As semiconductor heter-
ostructures, defi ning the distance over which an electron should propagate before the spin can
fl ip its orientation. As shown in Fig. 15.1 , the typical dimensions of InGaAs QDs are far smaller
than ᐍ
SO
and, thus, one would expect that SOI becomes increasingly ineffective as the confi ne-
ment lengthscales increase. Electron spin relaxation in bulk semiconductors is an ultra-fast proc-
ess, typically proceeding over timescales faster than 10 ps, primarily due to SOI mediated by
phonon or impurity scattering through the continuum of electronic states [81, 82] . However,
spin relaxation in QDs is expected to be slowed due to the weaker SOI, as discussed above, and
their discrete electronic structure that makes it much more diffi cult to fulfi l energy conservation
requirements during spin–fl ip [83, 84, 85] . While the precise mechanism driving spin relaxation
in QDs remains the subject of discussion, a number of workers have investigated theoretically
the comparative roles of linear spin–orbit interaction [83, 84, 85, 86] and hyperfi ne coupling to
the nuclear spin system [87, 88] . The scattering rate due to SOI has been shown to be suppressed
by several orders of magnitude in QDs due to their discrete electronic structure and the need,
therefore, for the participation of a limited spectrum of phonons to satisfy energy conservation
requirements [83, 84, 85, 88] . Under conditions of large static B -fi elds, the nuclear hyperfi ne
coupling perturbs only the precession frequency of the electron spin about the static fi eld direc-
tion, causing dephasing, but is not expected to fl ip the orientation of the electron spin and impact
upon T
1
[87, 88] .
These ideas from theory have been broadly supported by measurements of long spin lifetimes
for excitons in quantum dots, which essentially reveal no evolution of the exciton spin over its
radiative lifetime ( 1 ns) [89, 90] . However, such measurements are incapable of directly prob-
ing spin dynamics, since they are so slow, calling for investigations of single charges (electrons
and holes) in QDs for which radiative recombination cannot occur. The spin memory devices
investigated here provide a direct route towards the investigation of the electron and hole longi-
tudinal spin lifetimes.
15.3.3 Polarization dynamics as a probe of electron spin relaxation dynamics
Spin relaxation can be directly measured using spin memory devices: electrons are optically ini-
tialized in the higher energy Zeeman level by exciting the system with polarized light. The spin
relaxation time is then directly measured by monitoring the intensity of the emission recorded with
helicity as a function of the storage time ( I
,
(). In the absence of spin relaxation over the time one
should observe a strong polarization memory in the storage signal as discussed above. In contrast,
complete spin relaxation would result in steady-state spin populations of the two spin states accord-
ing to Boltzmann statistics, independent of the helicity of the optical excitation. For the low temper-
atures and high magnetic fi elds studied here, this would correspond to all electron spins occupying
CH015-I046325.indd 496CH015-I046325.indd 496 6/24/2008 5:06:34 PM6/24/2008 5:06:34 PM
Quantum Dot Charge and Spin Memory Devices 497
the lowest Zeeman level, or complete polarization of the storage EL. Reference to the data presented
in Fig. 15.16a confi rms that spin relaxation is slower than ~2 μ s at B 8 T and T 1 K .
Examples of such time resolved spin storage measurements, recorded at T 1 K and B 8 T,
are presented in Fig. 15.16b . The data shows the temporal evolution of the storage luminescence
intensity following σ excitation over the time range 0.001 ms 1 ms. Following excitation
with polarized light to pump electrons into the lower energy Zeeman level the storage EL is found
to be predominantly polarized as expected. Furthermore, it exhibits no detectable evolution up
to 1 ms ( Fig. 16b – upper panel) since the system is initialized close to thermal equilibrium. In
contrast, following excitation using polarized light, to generate electrons into the upper Zeeman
level, a very marked time dynamics of the luminescence polarization is observed ( Fig. 15.16b –
lower panel). For Δ t 0.001 the measurement reveals a maximum degree of circular polariza-
tion of DoP 61, decaying over time to a few per cent at Δ t 1 as electrons fl ip their spin
as depicted schematically in the fi gure. A very long spin lifetime of T
1
g
1 . 1 0.2 is obtained,
more than four orders of magnitude longer than spin–fl ip times for quantum wells and seven
orders of magnitude longer than the corresponding time in bulk III–V semiconductors.
In order to establish the mechanism driving spin–fl ip events we investigated the dependence
of T
1
on magnetic fi eld and the lattice temperature. The data recorded at T 1K is plotted in Fig.
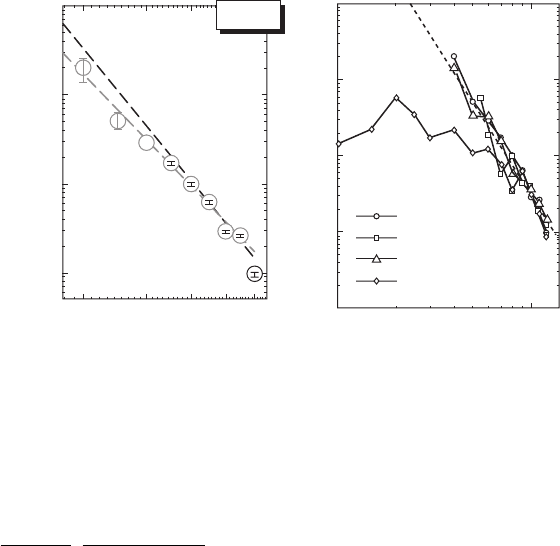
15.17a on a double logarithmic representation. The decay time constants extracted using the
above method are found to be strongly dependent on the magnetic fi eld, reducing dramatically
from T
1
2 0 6 m s a t B 4 T to 0.1 0.01 ms at 12 T. These data suggest a clear power-law
dependence T
1
B
m
. A least squares fi t to the data shown in Fig. 15.17a yields m 4.5 0.2.
We continue by discussing the origin of this very strong magnetic fi eld dependence. As discussed
in [83, 84] and [85] , one of the most signifi cant mechanisms driving spin–fl ip transitions is due
to spin–orbit coupling of the Zeeman levels via one-phonon scattering processes. In this case,
only vibrational modes with an energy E
ph
g
e
μ
B
B couple the two spin states.
±
T 1K
10
2
100
10
T
1
(ms) T (K)
0.1
0.01
1
10
1
10
0
10
1
B
4
B
5
B
4
4
110
6 8 10 12
Magnetic field (T) Magnetic field (T)
Spin–flip lifetime (ms)
(a) (b)
1K
10 K
20 K
30 K
Figure 15.17 (a) The evolution of the electron spin lifetime at T 1 K as a function of magnetic fi eld reproduced
with permission from [75] . (b) Measured electron spin lifetimes scaled with the lattice temperature at 1, 10, 20 and
30 K. The strong exponent and linear temperature dependence can clearly be seen.
The spin relaxation time can be calculated using perturbation theory and has the form [83]
TA
gB NET
1
4
5
1
1
()
() ()
ω
μ
sp
e B ph ph
, +
⎛
⎝
⎜
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
⎟
(15.2)
CH015-I046325.indd 497CH015-I046325.indd 497 6/24/2008 5:06:34 PM6/24/2008 5:06:34 PM

498 Handbook of Self Assembled Semiconductor Nanostructures for Novel Devices in Photonics and Electronics
where A is a dimensionless constant that refl ects the effective spin piezoelectric phonon coupling
strength in the material, * ω
sp
is the single particle s–p level spacing and N
ph
( E
ph
, T ) is the occupation
number of the phonon mode. At temperatures such that k
B
T g
e
μ
B
B , N
ph
reduces to N
ph
k
B
T /
g
e
μ
B
B and the spin lifetime becomes:
TA
gB kT
1
4
4
1
≈⋅
⎛
⎝
⎜
⎜
⎜
⎜
⎞
⎠
⎟
⎟
⎟
⎟
()
()
ω
μ
sp
eB B
(15.3)
Thus, the electron spin lifetime due to linear spin–orbit interaction mediated by one-phonon scat-
tering events should exhibit the following characteristics:
● Varies with magnetic fi eld according to T
1
B
4
.
● Varies with temperature according to T
1
(1/T) .
● Exhibits a very strong dependence on the dot size via ω
sp
.
Temperature dependent data T
1
e
is presented in Fig. 15.17b , and plotted in the form T
1
· T vs. -fi eld
for temperatures of 1 K, 10 K, 20 K and 30 K. For T , the experimental data plotted in this rep-
resentation is very similar, confi rming the temperature dependence predicted by Eq. 15.3 and a
magnetic fi eld exponent of m 4 . 5 0.2, close to the characteristic dependence predicted by
Eqs 15.2 and 15.3. When combined, these observations provide strong experimental evidence
that inter-Zeeman level spin–fl ip transitions in QDs are indeed dominated by SOI involving one-
phonon scattering processes at low temperature. The longest T
1
times measured of 2 0 m s a t
T 1 K and B 4 T are limited by the sensitivity of our optical detection scheme and represent a
lower limit. The absence of any observable saturation of T
1
in Fig. 15.17 suggests that the relaxa-
tion time could be much longer at lower fi elds. For example, extrapolating the observed T
1
B
4
dependency to lower fi elds would indicate T
1
8 0 m s a t 3 T, reaching 1 s at B 1.6 T. More
recent work on electrostatically defi ned QDs has revealed spin lifetimes in excess of seconds at
low temperatures [91] . Theoretical work has suggested that if spin orbit coupling mediated by
single phonons is the dominant spin scattering mechanism, then the spin coherence time should
approach the limit T
2
2 T
1
since fl uctuations of the effective magnetic fi eld are always perpen-
dicular to the applied magnetic fi eld [92] . However, recent studies have shown that this is not the
case since hyperfi ne coupling with the nuclear spin system dominates electron spin relaxation
and dephasing at lower magnetic fi elds [93] .
15.3.4 Hole spin relaxation in QDs
Unlike electrons, holes couple more weakly to the nuclear spins via the hyperfi ne contact inter-
action since they have p -like central cell symmetry [94] . This may provide an attractive route
towards hole–spin- based applications free from the complications caused by the fl uctuating nuclear
spin system. However, the hole–spin lifetime in III–V semiconductor nanostructures is generally
much shorter than discussed above due to strong SO mixing of heavy (HH) and light hole (LH)
valence bands [95, 96] . This mixing is inhibited by motional quantization effects and enhanced
hole–spin lifetimes have been reported for quantum wells ( 100 ps [97] ), extending beyond 1 ns
when optically driven spin heating effects are avoided [98] . For QD nanostructures, is expected to
become even longer due to the combined effects of bi-axial compressive strain and motional quan-
tization. These expectations have recently been supported by studies of negatively charged trions
in InAs [99] and CdSe [100] QDs, which indicate that
T
h
1
≥ ns
, limited by the timescale for radia-
tive recombination of the trions. Recent calculations have indicated that can become much longer
for isolated holes [101] , even exceeding in the limit when the energy separation between HH and
LH bands far exceeds the orbital quantization energy in the valence band [95] .
* Using typical material properties applicable to GaAs gives A 71, which together with reasonable values for
|| .g
e
08
and ω
sp
30 meV provide good quantitative agreement with our experimental data as indicated
by the dotted line in Figure 15.17.
CH015-I046325.indd 498CH015-I046325.indd 498 6/24/2008 5:06:35 PM6/24/2008 5:06:35 PM
