Ismail M., Koelink E. (editors) Theory and Applications of Special Functions

Подождите немного. Документ загружается.

THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS

[13]

New combinatorial interpretations of Ramanujan's partition congru-

ences mod 5,7 and 11, Trans. Amer. Math. Soc.

305

(1988), 47-77.

[14]

The crank of partitions mod 8,9 and 10, Trans. Amer. Math. Soc.

322

(1990), 79-94.

[15] M. D. Hirschhorn,

birthday present for Ramanujan, Amer. Math. Monthly

(1990), 398-400.

[16] D. M. Kane, Resolution of a conjecture of Andrews and Lewis involving cranks

of partitions, Proc. Amer. Math. Soc.

132

(2004), 2247-2256.

[17]

G. KaE and D.

Peterson, Infinite-dimensional Lie algebras, theta functions

and modular forms, Adv. in Math.

(1984), 125-264.

[18]

KaE and M. Wakimoto, Integrable highest weight modules over afine

superalgebras and number theory, Lie Theory and Geometry, Progr. Math., vol.

123, Birkhauser Boston, Boston, MA, 1994,

pp.

415-456.

[19] S. Ramanujan, Notebooks, vols.

Tata Institute of Fundamental Research,

Bombay, 1957.

[20]

The lost notebook and other unpublished papers, Narosa, New Delhi,

1988.

[21]

Tannery and

Molk, klkments de la Thgorie des Fonctions Elliptiques, Paris,

1898.

THE

SAALSCHUTZ

CHAIN

REACTIONS

AND MULTIPLE Q-SERIES

TRANSFORMATIONS

CHU Wenchang

Department of Applied Mathematics

Dalian University of Technology

Dalian 116024,

China

Current Address:

Dipartimento di Matematica

Universitci degli Studi di Lecce

Lecce-Arnesano

Box 193

73100 Lecce, ITALIA

chu.wenchang@unile.it

Abstract

recursive use of the q-Saalschiitz summation formula, we investigate

further the Saalschiitz chain reactions introduced by the author in (Chu,

2002). Some general series transformations which express basic termi-

nating series in terms of finite multiple sums will be established. As

applications, we derive

means of Jackson's BPS-series identity three

transformations including one due to Andrews (1975). These transfor-

mations yield further a number of multiple Rogers-Ramanujan identi-

ties, whose research was initiated and developed mainly by Andrews

and Bressoud from the middle of seventieth up to now.

Introduction and notation

For two complex numbers

and

the shifted-factorial of order

with base

is defined

(x;

q)O

1 and

(z;

q)n

x) (1

zq)

xqn-l)

for

1,2,

(l.la)

When

Iql

the infinite product

(x; q)m

J-Jl

xqk)

2005

Springer Science+Business Media,

Inc.

100

THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS

allows us consequently to express

where

can be an arbitrary real number.

The product and fraction forms of the shifted factorials are abbrevi-

ated throughout the paper respectively to

...

(a;

q),

. .

(c;

(1. le)

Following Bailey (Bailey, 1935) and Slater (Slater, 1966), the basic

hypergeometric series is defined by

where the base q will be restricted to Iql

for non-terminating q-series.

Among the basic hypergeometric formulas, we reproduce three of them

for our subsequent references. The first is the q-Saalschiitz theorem

(cf. (Bailey, 1935, Chapter 8) and (Slater, 1966, $3.3)):

The second is the very well-poised formula due to Jackson (cf. (Bailey,

1935, Chapter 8) and (Slater, 1966, 53.3)):

The third and the last one is Watson's q-analogue of the Whipple trans-

formation (cf. (Bailey, 1935, Chapter 8)):

The Saalschutz Chain Reactions and Multiple q-Series Transformations

101

The celebrated Rogers-Ramanujan identities (cf. (Slater, 1966, 53.5))

read as:

Bailey (Bailey, 1947; Bailey, 1948) discovered numerous identities of such

kind. A systematic collection was done by Slater (Slater, 1951; Slater,

1952). Some more recent results may be found in Gessel-Stanton (Gessel

and Stanton, 1983).

In their work on multiple Rogers-Ramanujan identities, Andrews and

Bressoud et al. (Agarwal et al., 1987; Andrews, 1984; Andrews, 1986;

Bressoud, 1980a; Bressoud, 1988) introduced the powerful Bailey chains

and Bailey lattice. They found general transformations which express

multiple unilateral sums into a single (unilateral) basic hypergeometric

series involving two sequences (Bailey pair) connected by an inverse se-

ries relation. The latter can be reformulated, in particular settings,

a bilateral basic hypergeometric series. By evaluating the bilateral sum

with the Jacobi triple or the quintuple product formulas, they derived

with great success many multiple Rogers-Ramanujan identities.

By iterating the q-Saalschutz formula (1.3),

the Saalschutz chain re-

actions

under "finite condition" has been introduced by the author in

(Chu, 2002) to study the ordinary and basic hypergeometric series with

integer differences between numerator and denominator parameters. We

will investigate further in the next section

the Saalschutz chain reactions

without finite condition and establish transformation theorems (from 2.4

to 2.7) of the same nature

Bailey chains due to Andrews and Bres-

soud but with one (or two) independent arbitrary sequence(s). Then we

proceed in Section 3 and 4 to derive explicitly several specific transfor-

mation formulas (without indeterminate sequence). Finally in the last

section, we conclude with thirty multiple Rogers-Ramanujan identities

which are simply limiting cases of the transformations presented in this

paper combined with the Jacobi triple product identity.

The purpose of this paper is not to present a general cover of the

Rogers-Ramanujan identities and their multiple counterparts through

the Saalschutz chain reactions.

Instead, it will be limited to illustrate

how to explore this method potentially to generate multiple basic hy-

102

THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS

pergeometric transformations and produce multiple Rogers-Ramanujan

identities.

The Saalschutz chain reactions

For nonnegative integers

with

and three indeterminates

the q-Saalschiitz formula

(1.3)

tells us that

which may be restated explicitly

follows:

Denote the multiple summation index and its partial sums respectively

(ml,

m2,.

. .

m,)

With

we may rewrite

(2.1)

with subscripts

Then the recursive product

(the Saalschutz chain reactions)

of the ex-

pression just displayed for

1,2,.

reasults compactly in the fol-

lowing

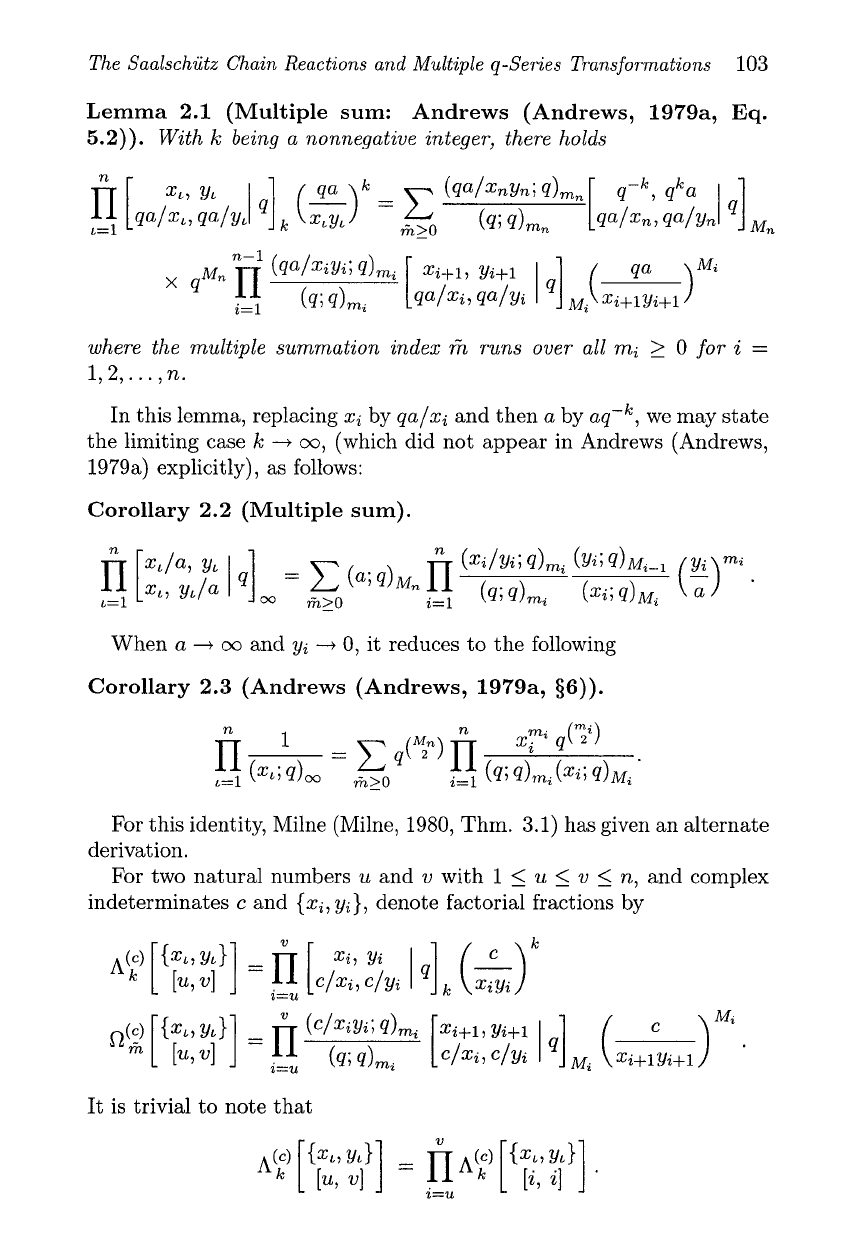
The Saalschiitz Chain Reactions and Multiple q-Series l?ransfomnations

103

Lemma 2.1 (Multiple sum: Andrews (Andrews, 1979a,

Eq.

5.2)).

With

being a nonnegative integer, there holds

where the multiple summation index

runs over all

for

1,2

,...,

In this lemma, replacing

qa/xi

and then

aq-5

we may state

the limiting case

co, (which did not appear in Andrews (Andrews,

1979a) explicitly), as follows:

Corollary 2.2 (Multiple sum).

When

co and yi

it reduces to the following

Corollary 2.3 (Andrews (Andrews, 1979a,

56)).

For this identity, Milne (Milne, 1980, Thm. 3.1) has given an alternate

derivation.

For two natural numbers

and

with

and complex

indeterminates

and {xi, yi}, denote factorial fractions by

It is trivial to note that

104

THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS

Then the multiple sum in the lemma may be expressed as

Multiplying both sides by

Mwk

for suitable

and then summing

over all

we establish the following general transformation theorem,

which may be considered

a counterpart of the main result obtained

in (Chu,

2002,

Thm. 2).

Theorem

2.4

(Well-poised transformation).

For a complex se-

quence

{Wk),

there holds the following multiple basic hypergeometric

transformation

provided that both series are well-defined and convergent.

Rewriting the well-poised transformation in Theorem

2.4

and then performing the substitution

The Saalschutz Chain Reactions and Multiple q-Series Transformations

105

we can manipulate the last sum (2.3c), shortly

S(2.3~) with respect

according to the formal series rearrangement

where

and

are forward and backward difference operators:

This can be proceeded

follows:

Now applying the transformation in Theorem 2.4 to the penultimate

line, we obtain with some simplification, the following expression

Replacing (2.3~) with this result leads (2.3) to the following almost-

poised series transformation.

Theorem

2.5

(Almost-poised transformation).

For two complex

sequences

{ak,

yk),

there holds the following multiple basic hypergeomet-

106

THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS

ric transformation

provided that both series are well-defined and convergent with

According to (2.4)) the k-sum in (2.5~) may be reformulated

where we have defined dually

In Theorem 2.5, take

Then it is easy to check the factorization

which leads us to the following transformation:

Theorem

2.6

(Almost-poised transformation).

For a complex se-

quence

{ak),

there holds the following multiple basic hypergeometric

The Saalschiitz Chain Reactions and Multiple q-Series Transformations

107

transformation

provided that both series are well-defined and convergent.

Taking instead in Theorem

2.5

we can compute without difficulty that

6k+Mn

(f)

k+Mn

which leads us to the following transformation:

Theorem

2.7

(Almost-poised transformation).

For a complex se-

quence

{Y~),

there holds the following multiple basic hypergeometric trans-

formation

provided that both series are well-defined and convergent.