Ismail M., Koelink E. (editors) Theory and Applications of Special Functions
Подождите немного. Документ загружается.


Painleve' Equations and Associated Polynomials
129
and a related many-body problem by Airault, McKean and Moser
(Airault et al., 1977) (see also (Adler and Moser, 1978)).
3. Rational solutions of the KdV equation (2.11) have the form (Ablowitz
and Satsuma, 1978; Adler and Moser, 1978; Airault, 1979; Airault
et al., 1977).
4. The Yablonskii-Vorob'ev polynomials are closely related with Schur
functions (Kajiwara and Ohta, 1996; Umemura, 2001) and so it
can be proved that the rational solution of
PII
can be expressed in
terms of determinants (Iwasaki et al., 2002; Kajiwara and Masuda,
1999a; Kajiwara and Ohta, 1996).
5.
Kametaka (Kametaka, 1983) has obtained a sharp estimate for the
maximum modulus of the poles of the Yablonskii-Vorob'ev poly-
nomials. It is shown that if A,
=
rna~~<~<,~,+~~/~{~a~,~~)
then
n2l3
5
An+2
<
4n2I3, for n
2
0. In (~aiecaka, 1985) Karnetaka
studies the irreducibility of the Yablonskii-Vorob'ev polynomials.
6. Kaneko and Ochiai (Kaneko and Ochiai, 2002) derive formulae
for the coefficients of the lowest degree term of the Yablonskii-
Vorob'ev polynomials; the other coefficients remain to be deter-
mined, which is an interesting problem.
Table
1.
Roots of the Yablonskii-Vorob'ev polynomials
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Roots of
Qz(z)
=
0
Roots of
Qg(z)
=
0
10
-2
-4
-6
-8
-lo
-8-6-4-2 0
2
4
6
8 10
Roots of
Q3(z)
=
0
10
1
0
,
,
,
;;::,
, ,
,
.
.
-2 . .
.
.
-4
-6
-8
-I0
-8-6-4-20
2
4
6
810
Roots of
QB(z)
=
0
Roots of
Qs(z)
=
0
Roots of
Q7(z)
=
0
Figure
1.
hots
of
the
Yablonskii-Vorob'ev polynomials
Q,(z)
=
0
2.2
Roots of the Yablonskii-Vorob'ev
polynomials
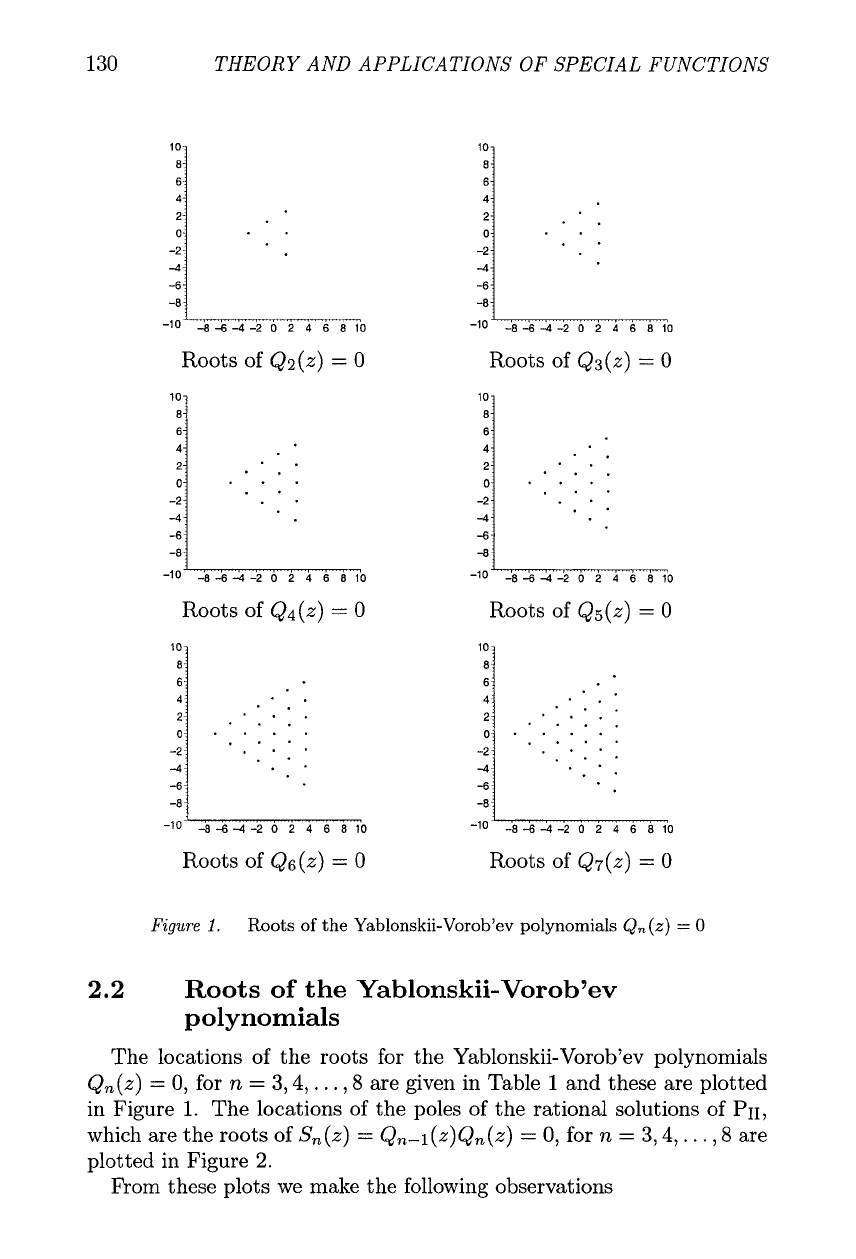
The locations of the roots for the Yablonskii-Vorob'ev polynomials
Qn(z)
=
0, for
n
=
3,4,
. . .
,8 are given in Table
1
and these are plotted
in Figure
1.
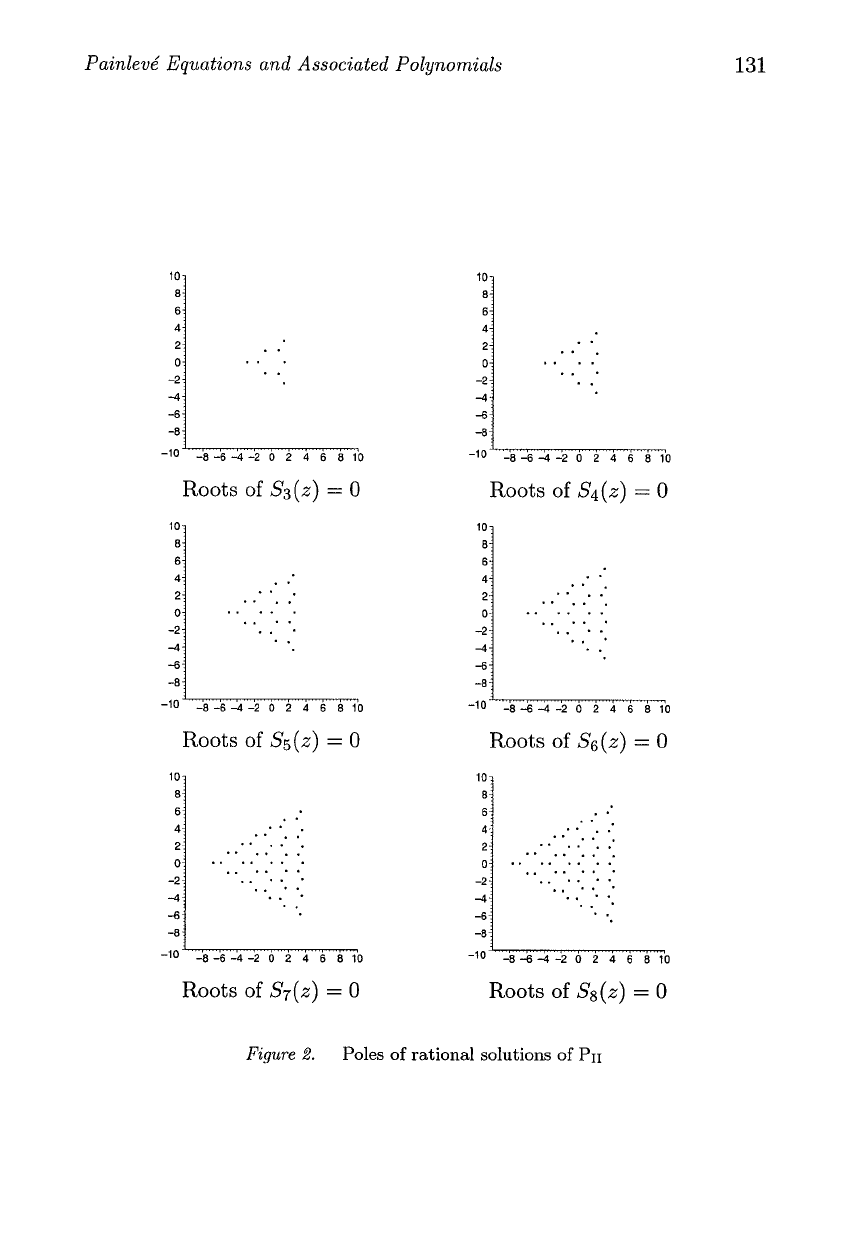
The locations of the poles of the rational solutions of
PII,
which are the roots of
S,(z)
=
Qn-l(z)Qn(z)
=
0, for
n
=
3,4,
.
.
.
,8 are
plotted
in
Figure
2.
From these plots we make the following observations
Painleve' Equations and Associated Polynomials
-lo
-8
-k
A
-2
0
2
4
6
8
(0
Roots of
S3(z)
=
0
Roots of
S5(z)
=
0
Roots of
&(z)
=
0
Roots of
S4(z)
=
0
Roots of
Ss(z)
=
0
Figure
2.
Poles of rational solutions of
PII

132
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
1.
From Figure
1
we see that the roots of the Yablonskii-Vorob'ev
polynomials form approximately equilateral triangles, in fact ap-
proximate "Pascal triangles." The values of the roots in Table 2.1
show that they actually lie on curves rather than straight lines.
2. The roots of Qn(z)
=
0
lie on circles with centre the origin. If we
define
if
n
$
lmod 3,
qn(O
=
{
if
n
-
1
mod 3.
The radii of the circles are given by the third roots of the absolute
values of the non-zero roots of qn(<)
=
0, with three equally spaced
roots of Q,(z)
=
0 on circles for the real roots of qn(<)
=
0 and
six roots, three complex conjugate pairs, of Qn(z)
=
0
on a circles
for the complex roots of qn(<)
=
0
(see (Clarkson and Mansfield,
2003)).
3. The plots in Figures
1
and
2
are invariant under rotations through
$.ir
and reflections in the real z-axis and the lines arg(z)
=
f
$r,
f
$7~.
This is because
PII
admits the finite group of order
6
of scalings
and reflections
where
p3
=
1
and
E~
=
1.
4. From Figure 2 we see that the poles of the rational solutions of
PII
that the location of the poles yields an approximate triangle
structure, with internal hexagons.
3.
Third Painlev6 equation
3.1
Rational solutions of PIII
In this section we consider the generic case of
PIII
when y6
#
0, then
we set
y
=
1
and 6
=
-1,
without loss of generality (by rescaling
w
and
z if necessary), and so consider
The location of rational solutions for the generic case of
PIII
given by
(3.1) is stated in the following theorem.
Theorem
3.1.
Equation
(3.1),
i.e.,
PIII
with
y
=
-6
=
1,
has rational
solutions
if
and only
if
a
+
ED
=
4n,
with
n
E
Z
and
E
=
f
1.
These

Painleve' Equations and Associated Polynomials
133
rational solutions have the form
w
=
Pm(z)/Qm(z),
where
Pm(z)
and
Q,(z)
and polynomials of degree
m
with no common roots.
Proof
See Gromak, Laine and Shimomura (Gromak et al., 2002), p. 174
(see also (Milne et al., 1997; Murata, 1995; Umemura and Watanabe,
1998)).
We remark that the rational solutions of the generic case of PIII (3.1)
lie on lines in the
a-p
plane, rather than isolated points as is the case for
PIv (see
94).
Further, equation (3.1) is of type
D6
in the terminology
of Sakai (Sakai, 2001), who studied the Painlev6 equations through a
geometric approach based on rational surfaces.
Umemura (Umemura, 2003), see also (Kajiwara and Masuda, 199913;
Noumi M. and
H.,
1998; Umemura, 1998; Umemura, 2001), derived spe-
cial polynomials associated with rational solutions of
PIII,
which are
defined in Theorem 3.2 below. Further Umemura states that these poly-
nomials are the analogues of the Yablonskii-Vorob'ev polynomials as-
sociated with rational solutions of
PII
and the Okamoto polynomials
associated with rational solutions of PIv.
Theorem
3.2.
Suppose that
Tn(z; p)
satisfies the recursion relation
with
T-l(~; p)
=
1
and
To(z; p)
=
1.
Then
satisfies
PIII,
with
an
=
2n
+
2p
-
1
and
,On
=
2n
-
2p
+
1.

134
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
The first few polynomials for
PI1l
defined by (3.2) are
and associated rational solutions of
PIII
are
The hierarchy of rational solutions of
PIII
given in (3.5) can also be
derived using the Backlund transformation of
PIII
given by
where
w
-
w(z;
a,
p,
1,
-I),
6
=
a
+
2 and
=
,O
+
2 (Gromak, 1973;
Gromak, 1975) (see also (Milne et al., 1997; Murata, 1995; Umemura

Painleve' Equations and Associated Polynomials
and Watanabe, 1998)), i.e.,
where w,
-
w(z;
a,,
P,,
1,
-I),
a,
=
2n
+
2p
-
1
and
Pn
=
2n
-
2p
+
1,
with "seed solution" ~~(z;cro,/?~;
1; -1)
=
1
where
a0
=
2p
-
1
and
Po=
-2p+1.
The polynomials Tn(z) are somewhat unsatisfactory since they are
polynomials in
J
=
l/z rather than polynomials in z, which would be
more natural and is the case for the Yablonskii-Vorob'ev polynomials
and Okamoto polynomials associated with rational solutions of
PII
and
PIv, respectively. However it is straightforward to determine a sequence
of functions S,(z) which are generated through a Toda equation that
are polynomials in z. These are given in the following theorem.
Theorem
3.3.
Suppose that
S,(z; p)
satisfies the recursion relation
(
Toda equation)
with
S-l
(z; p)
=
SO
(z; p)
=
1.
Then
satisfies
PIII
with
a,
=
2n
+
2p
-
1
and
P,
=
2n
-
2p
+
1.
Proof.
This essentially follows from Theorem
1
due to Kajiwara and
Masuda (Kajiwara and Masuda, 199913) since the Toda equation (3.8),
modulo a scaling factor, is equation (16) in Proposition 3 of (Kajiwara
and Masuda, 199913).

136
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
The first few polynomials
Sn(z;
p),
which are monic polynomials of
degree
$n(n
+
I),
are
S1(z;p)
=
2
+
p,
S2(z;p)
=
(2
+
pI3
-
P,
S3k;
=
(
2
z
+
P)~
-
542
+
pI3
+
9p(z
+
p)
-
5p
,
s4(z;
P)
=
(2
+
P)
lo
-
15p(z
+
p)7
+
63p(z
+
p)5
-
225p(z
+
p)
3
+
315p2(z
+
p)2
-
175p3(z
+
p)
+
36p2,
S5(z;
p)
=
(z
+
p)15
-
35p(z
+
p)12
+
252p(z
+
p)1°
+
175p2(z
+
p)'
-
2025p(z
+
p)8
+
945p2(z
+
p)7
-
1225p(p2
-
9)(2
+
p)6
-
26082p2(z
+
,LL)~
+
33075p3(z
+
,LL)~
-
350p2(35p2
+
36)(z
+
p)3
+
11340p3(z
+
p)2
-
225p2(49p2
-
36) (z
+
p)
+
7p3 (875p2
-
828).
(3.10)
The associated rational solutions of
PIII
are in
(3.5).
It is clear from the
recurrence relation
(3.8)
that the
Sn(z; p),
are rational functions, though
it is not obvious that in fact they are polynomials since one is dividing
by
Sn-l (z;
p)
at every iteration. Indeed it is somewhat remarkable that
the
Sn(z;
p)
defined by
(3.8)
are polynomials. The polynomials
S,(z; p)
defined by
(3.8)
are related to the polynomials
R,
(z;
p)
defined by
(3.2)
through
Sn
(z; p)
=
zn(n+1)/2
R,
(z;
p)
.
The polynomials
Sn
(z;
p)
have
the property that
Sn(z;
p)
=
Sn(-z;
-p).
In Figure
3
plots of the roots of the polynomial
&(I
-
p,
p)
defined
by
(3.10)
for various
p
are given. Initially for
p
=
-3
there is an ap-
proximate triangle of roots with
4
roots on each side. As
p
increases,
sets of roots then in turn coalesce until there is a multiple root of order
10
for
m
=
0.
Then as
p
another approximate triangle appears which is
"turned round'' from the configuration for
p
=
-3
since the symmetry
is
S,(z;
p)
=
Sn(-z; p)
implies that the roots for
Sn(z;
p)
is a reflection
of those for
S,(z;
-p)
in the imaginary axis.
0
3.2
Algebraic solutions of
PIII
In this section we consider the special case of
PIII
when either (i),
y
=
0
and
ad
#
0,
or (ii),
6
=
0
and
@y
#
0.
In case (i), we make the
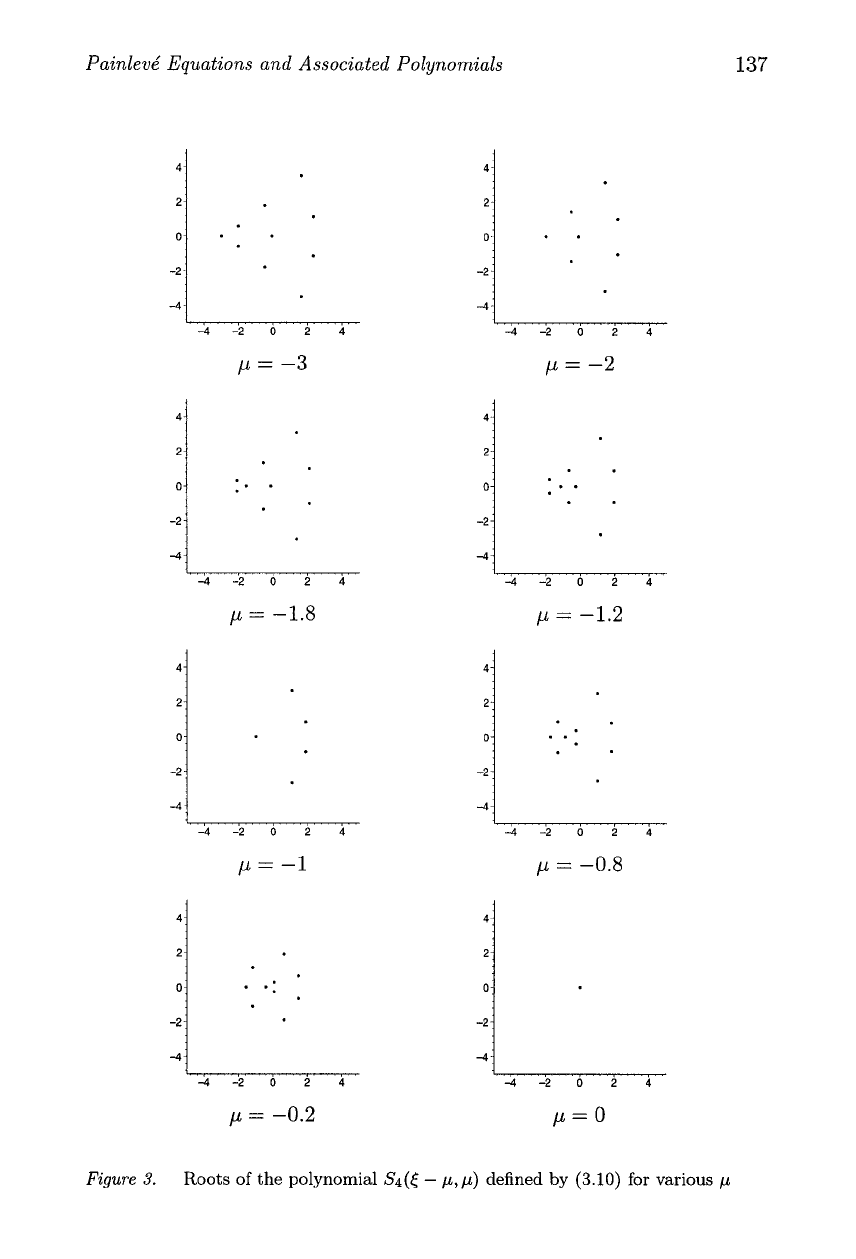
Painlevk Equations and Associated Polynomials
Figure
3.
Roots of
the
polynomial
S4([
-
p, p)
defined
by
(3.10)
for various
p

138
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
transformation
and set
a
=
1,
,6
=
2p and
6
=
-1,
with p an arbitrary constant,
without loss of generality, which yields
In case (ii), we make the transformation
and set
a
=
2p,
,6
=
-1
and
y
=
1,
with p an arbitrary constant, without
loss of generality, which again yields (3.12). The scalings in (3.11) and
(3.13) have been chosen so that the associated special polynomials are
monic polynomials. We remark that equation (3.12) is of type
D7
in the
terminology of Sakai (Sakai, 2001).
Rational solutions of (3.12) correspond to algebraic solutions of PIII
with
y
=
0 and
a6
#
0, or
6
=
0 and
,6y
#
0. Lukashevich (Lukashevich,
1965; Lukashevich, 1967a) obtained algebraic solutions of
PIII,
which are
classified in the following theorem.
Theorem
3.4.
Equation
(3.12)
has rational solutions
if
and only
if
p
=
n,
with
n
E
Z.
These rational solutions have the form
u(5)
=
Pn2+l
(<)/Qn2
(<),
where
Pn2+l
(5)
and
Qn2
(5)
and monic polynomials of
degree
n2
+
1
and
n2,
respectively.
Proof.
See Gromak, Laine and Shimomura (Gromak et al., 2002), p. 164
(see also (Gromak, 1973; Gromak, 1978a; Milne et al., 1997; Murata,
1995)).
A
straightforward method for generating rational solutions of (3.12)
is through the Backlund transformation
where
E~
=
1
and up is the solution of (3.12) for parameter p, using the
"seed solution" uo(5)
=
5
for p
=
0 (see Gromak, Laine and Shimomura
(Gromak et al., 2002)) p. 164 -see also (Gromak, 1973; Gromak, 1978a;
Milne et al., 1997; Murata, 1995)).
Further we note that
ti-,(<)
=
-iu,(i('). Therefore the transformation group for (3.12) is isomorphic to
