Ismail M., Koelink E. (editors) Theory and Applications of Special Functions
Подождите немного. Документ загружается.


108
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
3.
Basic Almost-poised Transformations
By specifying the
W
and
a,
y-sequences in the transformation theo-
rems established in the last section, we will derive three explicit multiple
series transformations which exemplify a larger class of such relations.
In Theorem 2.4, take
Then the inner sum with respect to
k
becomes
with the 6p5-series evaluated by Jackson's formula
as
This leads us to the following
Theorem
3.1
(Andrews (Andrews, 1975, Theorem
4)
and (An-
drew~, 1979a, 95)).
For complex parameters {a,
b,
c, d), and indeter-
minates {xk, yk)EZ1 with
X
=
xlx2..
.
xn and
Y
=
yly2. yn, there
holds the multiple basic hypergeometric series transformation
provided that both series are well-defined and terminated
by
one of
b,
c
or d.
In Theorem 2.6, take

The Saalschiitz Chain Reactions and Multiple q-Series Transformations
109
Then the sum with respect to
k
in
(2.9d)
becomes
with the 6q5-series under terminating condition evaluated as
Substituting these into Theorem
2.6,
we get the following transforma-
tion:
Theorem
3.2
(Almost-poised transformation).
There holds the
multiple basic hypergeometric transformation
provided that both series are well-defined and terminated by one of
b,
c
or d.
In Theorem
2.7,
take

110
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Then the sum with respect to
k
in (2.10d) becomes
with the 6cps-series under terminating condition evaluated as
Substituting these into Theorem 2.7, we get the following transform*
tion:
Theorem
3.3
(Almost-poised transformation).
There holds the
multiple basic hypergeometric transformation
provided that both series are well-defined and terminated by one of b, c
or d.
4.
Reductions and Consequences
The transformations displayed in the last section may be reduced by
limiting process to several known and unknown results as consequences.
4.1
George Andrews
In Theorem 3.1, let
c
t
oo
and xi, yi
+
oo
for
i
=
2,3,.
. .
,
n.
The
result may be stated as
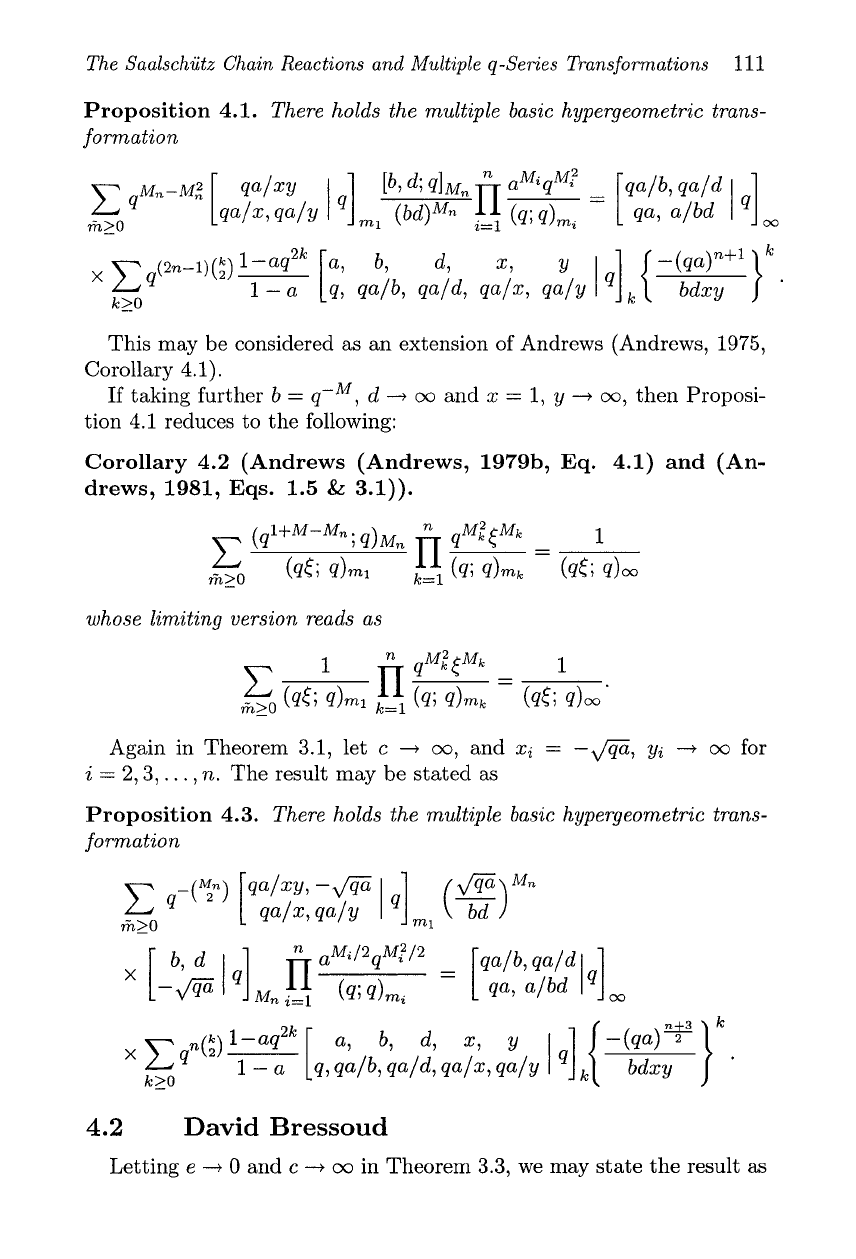
The Saalschiitz Chain Reactions and Multiple q-Series Bansformations
111
Proposition 4.1.
There holds the multiple basic hypergeometric trans-
formation
n
Q+Y
[b, d; qlMn aMiqMj qalb, qald
x
qMn-M'
[R~/x,
Q~/Y
I
q]
(bdJMn
(q; q)mi
Th20
z=1
=
[
qa, a/M Iq]_
This may be considered as
an
extension of Andrews (Andrews,
1975,
Corollary
4.1).
If taking further
b
=
qVM, d
--+
oo
and
x
=
1, y
t
oo,
then Proposi-
tion
4.1
reduces to the following:
Corollary 4.2 (Andrews (Andrews, 1979b, Eq. 4.1) and (An-
drew~, 1981, Eqs. 1.5
&
3.1)).
whose limiting version reads as
Again in Theorem
3.1,
let c
+
oo,
and
xi
=
-@,
yi
-t
oo
for
i
=
2,3,.
. .
,
n.
The result may be stated
as
Proposition 4.3.
There holds the multiple basic hypergeometric trans-
formation
4.2
David
Bressoud
Letting
e
t
0
and
c
+
oo
in
Theorem
3.3,
we may state the result as
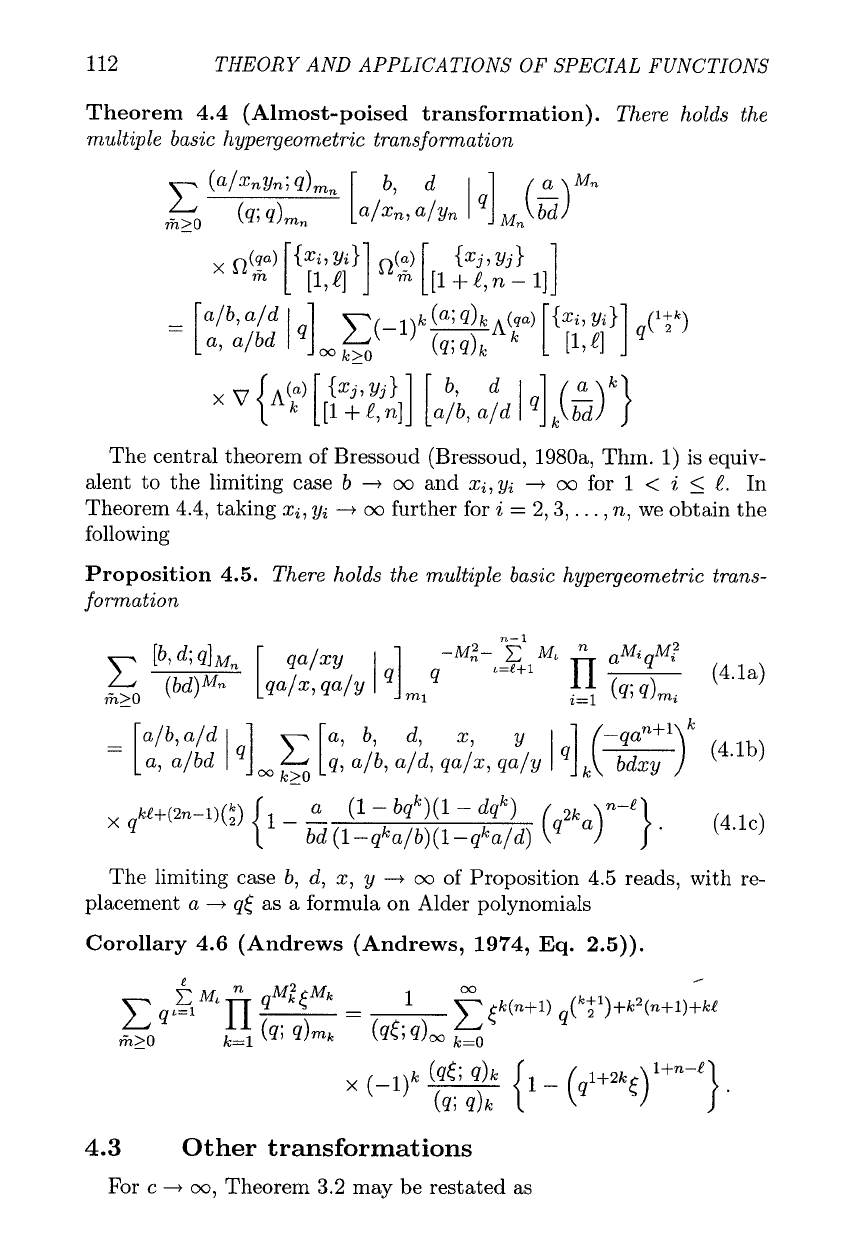
112
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Theorem 4.4 (Almost-poised transformation).
There holds the
multiple basic hypergeometric transformation
alb, ald
=
[a, a/bd
I
'1
C(-')
k
q)k
"1
[{T~:
q(l:k)
O0
k>O
(4;
dk
The central theorem of Bressoud (Bressoud, 1980a, Thm. 1) is equiv-
alent to the limiting case
b
-+
oo and xi, yi
+
oo for
1
<
i
5
e.
In
Theorem 4.4, taking xi, yi
-+
oo further for
i
=
2,3,.
. .
,
n,
we obtain the
following
Proposition 4.5.
There holds the multiple basic hypergeometric trans-
formation
alb, ald
=
[a, a/,,
I
q]
c
[
a,
b,
d, x,
00
k20
lq],(-E)" (4.lb)
4, alb, ald,
PIX,
qaly
The limiting case b, d, x, y
+
oo of Proposition 4.5 reads, with re-
placement a
+
qJ as a formula on Alder polynomials
Corollary 4.6 (Andrews (Andrews, 1974,
Eq.
2.5)).
4.3
Other transformations
For c
+
oo, Theorem
3.2
may be restated
as

The Saalschiitz Chain Reactions and Multiple q-Series l?ransformations
113
Theorem
4.7
(Almost-poised transformation).
There holds the
multiple basic hypergeometric transformation
Its further limiting case
xi, yi
-+
oo
for
i
=
2,3,.
. .
,
n
reads as
Proposition
4.8.
There holds the multiple basic hypergeometric trans-
formation
Letting
c, e
-+
oo
in Theorem
3.3,
we may state the result
as
Theorem
4.9
(Almost-poised transformation).
There holds the
multiple basic hypergeometric transformation
alb,
aid
(a;
q)k
(qa)
{xi, ~i}
-(;I
=
[a, a/bd
1
co
k20
(2)
[
[I,
*]
]

114
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Its further limiting case xi7 yi
--t
co
for
i
=
2,3,.
. .
,
n of this theorem
reads
as
Proposition 4.10.
There holds the multiple basic hypergeometric trans-
formation
n-1
[b,
d;
911
M~
qa/x
Y
-M;-
.=e
C
M,
n
aMi 4 Mf
(bd)
Mn
[qa/x7
P/Y
1
'1
m:
s20
i=, (4; 4)mi
5.
Multiple Rogers-Ramanujan Identities
Under various specifications, the k-sums appeared in the propositions
demonstrated in last section may be evaluated in closed forms by the
Jacobi triple product identity (cf. Bailey (Bailey, 1935, Chapter
8))
which allows us to derive the following multiple Rogers-Ramanujan iden-
tities:
Example
1
(a
=
1:
b,
d
+
oo
and
x, y
=
f
q1/2
in Proposition 4.1).
Example
2
(a
=
q:
b,
d
--t
oo
and
x, y
=
f
q1I2
in Proposition 4.1).
Example
3
(a
=
q: x
=
-q
and
b,
d,
y
-t
oo
in Proposition
4.5).

The Saalschiitz Chain Reactions and Multiple q-Series Transformations
115
It has first been discovered in (Agarwal and Bressoud, 1989, Eq. 1.1),
(Bressoud, 1980a, Eq. 3.4), (Bressoud, 1980b, Thm. 1:
S
=
0), (Bressoud,
1981, Eq. 5.6), (Bressoud, 1989, Eq. 1.1) and (Bressoud et al., 2000,
p.
7-
2)
by Bressoud et al.
Example 4 (a
=
q: x
=
-q
and
b,
dl
y
+
oo
in Proposition 4.8;
cf.
(Stembridge, 1990,
Eq.
1-11)).
Example 5 (a
=
q:
b,
dl x,
y
-t
oo
in Proposition 4.5).
As a common generalization of the Rogers-Ramanujan identities (1.5a)-
(1.5b), this one has been found in (Agarwal et al., 1987, Eq. 1.5), (Agar-
wal and Bressoud, 1989, Eq. 0.3), (Andrews, 1974, Eq. 1.7), (Andrews,
1976, Eq. 7.3.7), (Andrews, 197913, Eq.
1.3), (Andrews, 1981, Eq. 1.1),
(Andrews, 1984, Eq. 1.3), (Andrews, 1986, Eqs. 3.45-46), (Bressoud,
1980a, Eq. 3.2), (Bressoud, 1980b, Thm. 1:
b
=
I), (Bressoud, 1981,
Eqs. 5.3
&
6.1), (Bressoud, 1989, Eq. 0.3), (Bressoud et al., 2000,
pp.
4-1
&
7-I), (Garrett et al., 1999, Eq. 4.1) and (Stembridge, 1990, Eqs. c-d)
mainly by Andrews and Bressoud et al.
Example
6
(a
=
q:
b,
d, x,
y
+
oo
in Proposition 4.8).
Example
7
(a
=
q:
b
=
-9, d
-t
oo
and
x,
y
=
f
q1I2
in Proposi-
tion 4.3).
Example 8 (a
=
q:
b
=
-9, d
-+
oo
and
x,
y
=
f
q1I2
in Proposi-
tion 4.1).

116
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Example
9
(a
=
1:
b
=
-q,
d
-t
co
and
x
=
y
=
-1
in Proposi-
tion 4.1).
Example 10
(a
=
q:
b
=
x
=
-q
and
d,
y
-+
co
in Proposition 4.8).
~~~~~l~ 11
(a
=
q:
"-v,
z=ql,2,
d=-q1L/2
y__
I
q
-)
q2
in Proposition 4.3).
Example 12
(a
=
q:
b
=
-q
and
d,
x,
y
-t
co
in Proposition 4.8).
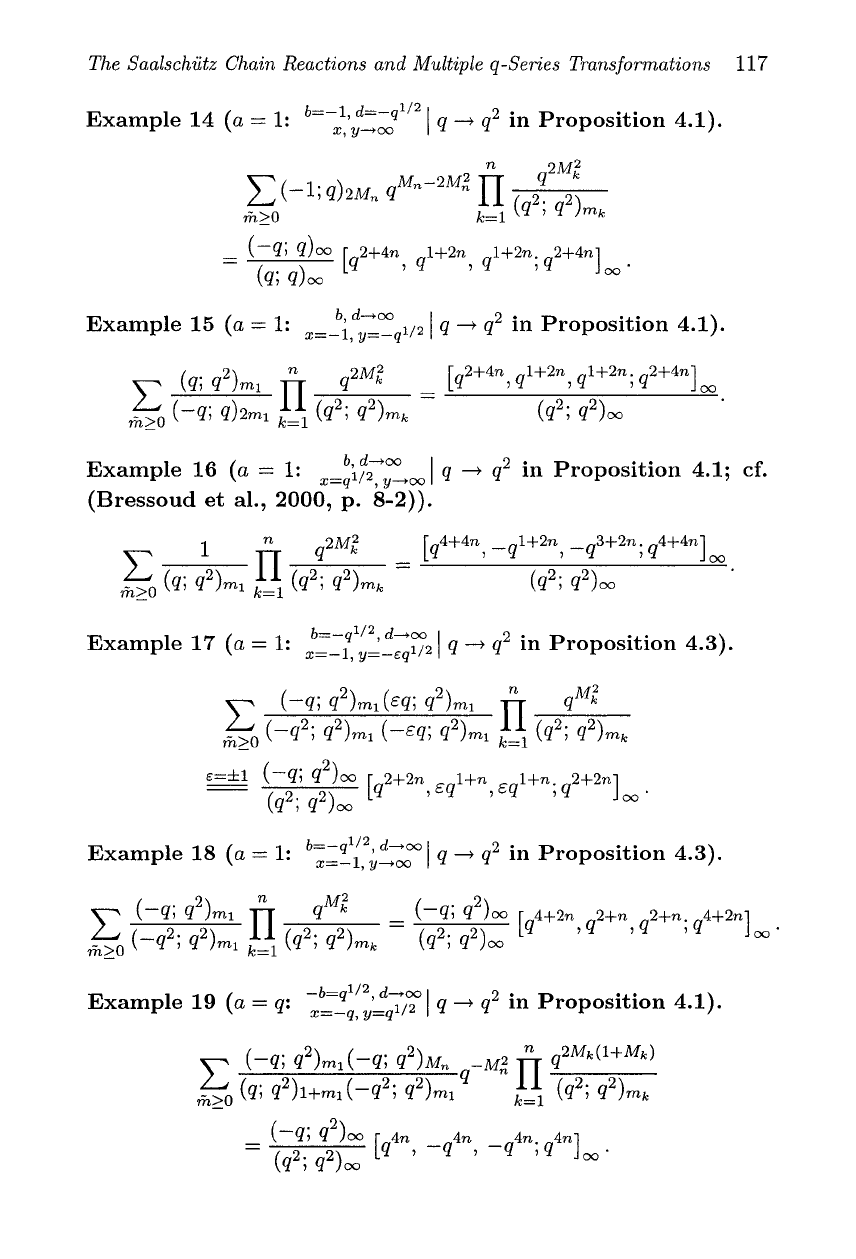
The Saalschutz Chain Reactions and Multiple q-Series Transformations
117
Example 15 (a
=
1:
b, d4co
x=-1, y=-q
I
q
+
q2
in Proposition 4.1).
b d+oo
Example 16 (a
=
1:
x=;1,2
1
q
+
q2
in Proposition 4.1;
cf.
r
Y+,
(Bressoud et al., 2000, p. 8-2)).
Example 17 (a
=
1:
b=-q
d400
x=-~,
y=-+/2
1
q
+
q2
in Proposition 4.3).
b=-q1/2, d4,
Example 18 (a
=
1:
x=-l,
y+03
I
q
+
q2
in Proposition 4.3).
-b=q'/2, d-,,
Example 19 (a
=
q:
x=-
q, y=q1l2
I
p
+
q2
in Proposition 4.1).
