Ismail M., Koelink E. (editors) Theory and Applications of Special Functions
Подождите немного. Документ загружается.

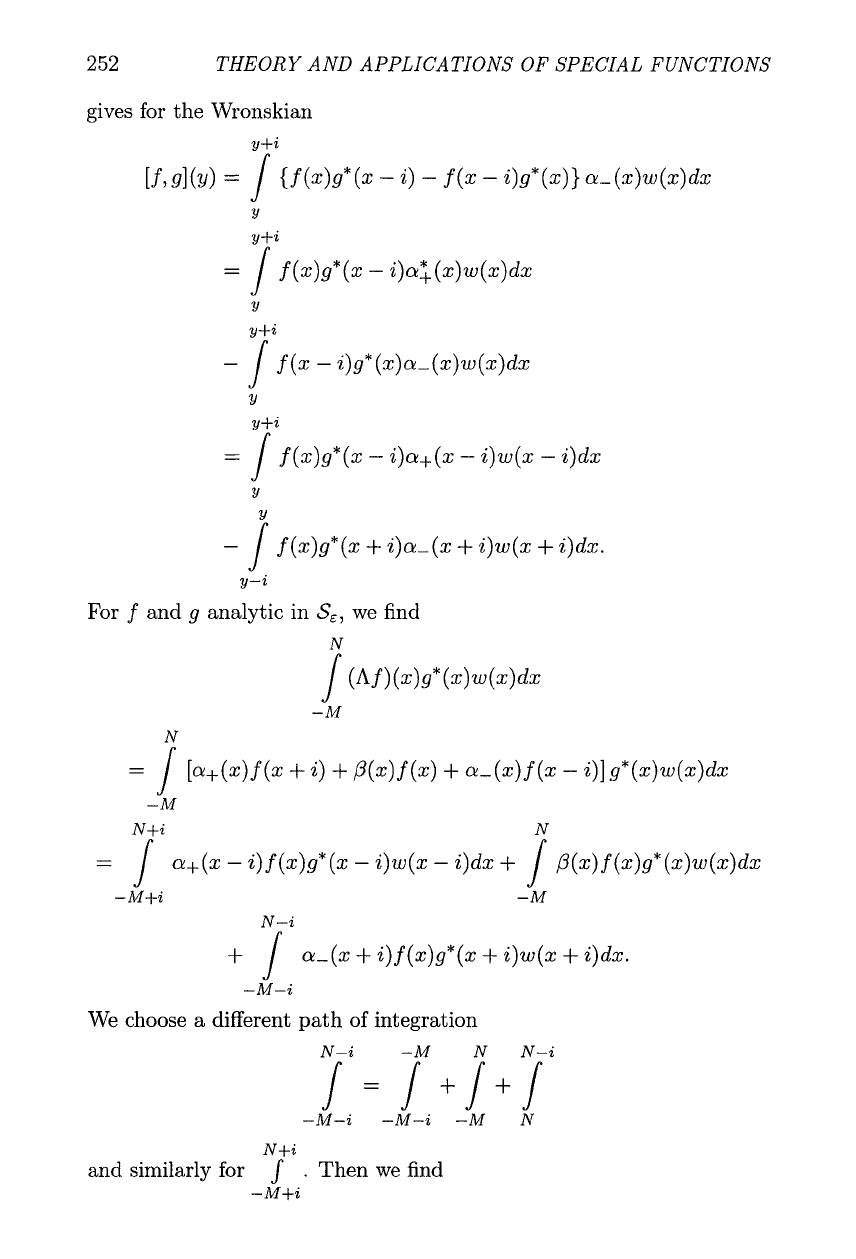
252
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
gives for the Wronskian
-
]
~(X)~*(X
+
i)a-(x
+
i)w(x
+
i)dx.
y-i
For
f
and
g
analytic in
S,,
we find
+
a-(x
+
i)
f
(x)g*(x
+
i)w(x
+
i)dx.
-
M-i
We choose a different path of integration
N+i
and similarly for
J
.
Then we find
-M+i
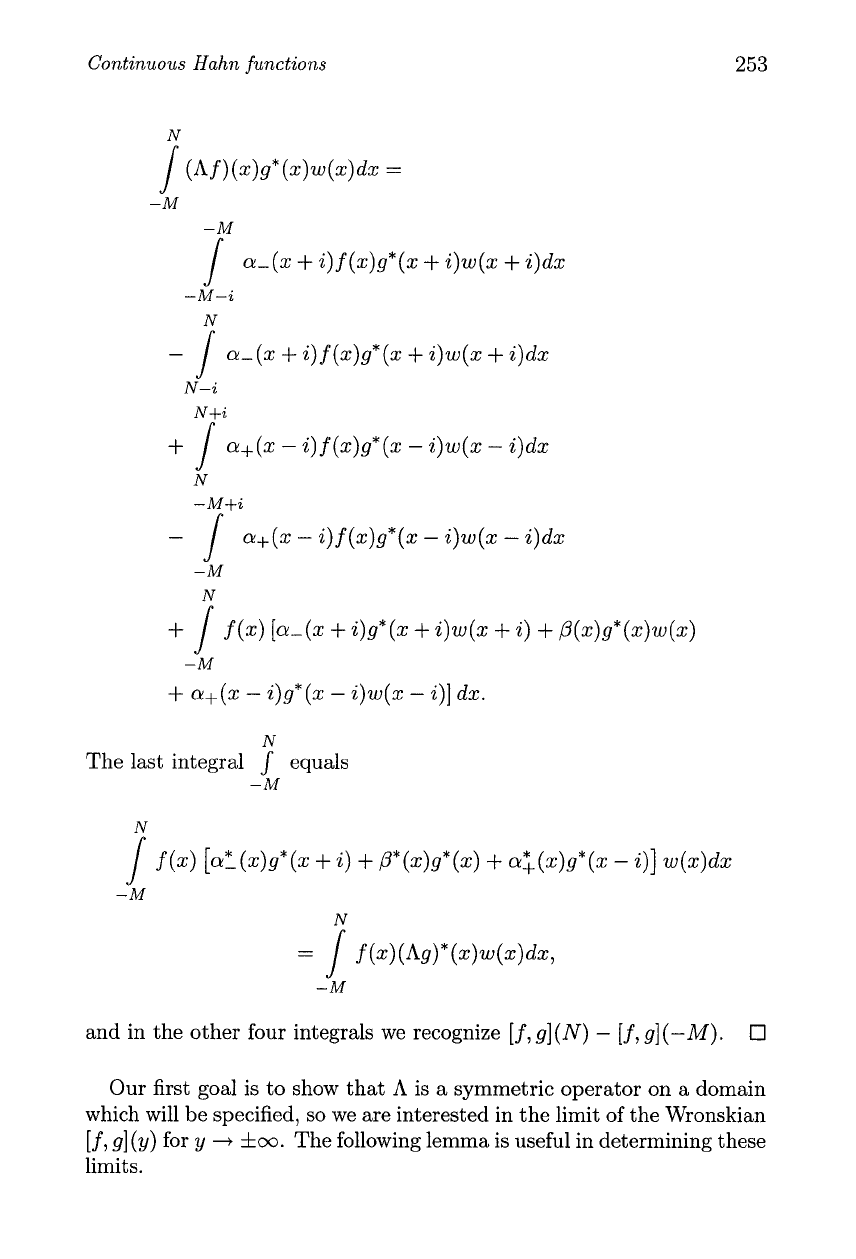
Continuous Hahn functions
a-(x
+
i)
f
(x)g*(x
+
i)w(x
+
i)dx
-M-i
N
+
a+(.
-
i)g*(x
-
i)w(x
-
i)]
dx.
N
The last integral
J
equals
-M
and in the other four integrals we recognize [f,g](N)
-
[f,
g](-M).
Our first goal is to show that
A
is a symmetric operator on a domain
which will be specified, so we are interested in the limit of the Wronskian
[f,
g] (y) for y
--+
f
oo.
The following lemma is useful in determining these
limits.

254
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Lemma
5.4.
Let
kl,
k2
>
1,
x
E
R, and
-1
5
y
5
1,
then the weight
function w(x
+
iy) has the following asymptotic behaviour
w(x
+
iy)
=
Proof. From Stirling's asymptotic formula (Olver, 1974, (8.16)) we find
for u
>
0 and v
E
R
We use
v
arctan
-
+
arctan
-
=
U
v
2'
v<o,
to find for v
-t
f
oo
v
(iu
-
v) arctan
-
=
(iu
-
v)
(k
U
2 v
SO we have, for v
+
f
00,
Applying this formula to the four I?-functions in (5.1) gives the asymp-
totic behaviour of the weight function w(x
+
iy).
0
In general, if for some
E
>
0
then the moment problem for the measure dp is determinate, see, e.g.,
(de Jeu, 2003) and references therein. Using this criterion with
0
<
E
<
min{4cp, 4(7r
-
cp)), we find from Lemma 5.4 that the moment problem
for the measure w(x)dx is determinate. In particular this shows that
the polynomials are dense in L2 (R, w(x)dx).
Let
2)
be the space of polynomials on
R,
then
27
is a dense subspace
of L2(R, w(x)dx). Since
a-
(x
+
iy)
=
e-2i'+'x2
(
1
+
O
(:))
3
x
-+
fm)
(5.21

Continuous Hahn functions
255
it follows from Definition 5.2 and Lemma 5.4 that
lim
[f,
g](N)
=
0
N-tfco
for
f,
g polynomials. Hence by Proposition 5.3 we find
Proposition
5.5.
The operator (A,D) is a densely defined symmetric
operator on
L~(IW,
w(x)dx).
Remark
5.6.
The operator (A,
2))
is also densely defined and symmetric
on the space spanned by e-x(2~-T)pn(x), where pn is a polynomial, cf.
Remark 5.1.
5.2
Eigenfunctions of
A
We determine eigenfunctions of A, using contiguous relations for 3F2-
functions. First note that for a monic polynomial of degree
n,
pn(x)
=
xn
+
- -
.
,
we have
(Ap,) (x)
=
[a+(x)
+
P(x)
+
a-
(x)] xn
+
lower order terms.
Since
a+(%)
+
P(x)
+
a-(x) is a polynomial of degree 2, A raises the
degree of a polynomial by 2. Therefore A cannot have polynomial eigen-
functions.
Let p(x) be the i-periodic function
1
p(x)
=
-en" sin
(7r
(kl
-
it
-
ix))
,
7r
(5.3)
and let cpp(x)
=
cpp
(x;
t,
kl, k2,
(P)
and @,(x)
=
@,
(x;
t,
kl, k2,cp) denote
the functions
I?
(1
-
kl
+
it
+
ix)
cpp(x)
=
e-2qxp(x)
I?
(kl
+
ix
+
it)
3F2
(k2
-
ix, k2
-
kl
+
i
+
ip,
k2
-
k
+
-
ip
(5.4)
252, k2
-
kl
+
it
+
1
I?
(1
-
kl
+
it
+
ix)
I?
(1
-
k2
+
ix)
@,(x)
=
e-2'xp(x)
I?
(kl
+
ix
+
it)
I?
(2
-
kl
+
ix
+
ip)
3
k2
-
k1
+
i
+
ip,
2
-
k1
-
k2
+
ip,
4
-
it
+
ip
1
+
2ip,
-
kl
+
ix
+
ip
(5.5)
Both 3F2-series are absolutely convergent for
%!
(kl
+
it
+
ix)
>
0.
Note
that the expression for cp,(x) is the same
as
(4.9) after applying Euler's
reflection formula.
Proposition
5.7.
For kl
>
1, the functions
(P,(x)
and <Pp(x) are eigen-
functions of A for eigenvalue
(p2
+
a).

256
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Remark
5.8.
(i) Observe that due to the i-periodic function p(x), yp(x) is an entire
function. Denote @,(x)
=
9,(x)/p(x), then p(x) cancels the poles
of @,(x). There are more choices of i-periodic functions that cancel
the poles of @,(x). One of the reasons for this particular choice, is
that
it
appears
in
the Lie-algebraic interpretation of the function
vp(x), see Theorem 4.5. We come back to the choice of the
i-
periodic function
in
Remark 5.15.
(ii) Observe that cp;(x) is obtained from
(P,(X)
by the substitutions
(x,
t,
9)
H
(-2,
-t,
T
-
9).
Since the diflerence operator
A
and
the weight function w(x) are invariant under these substitutions,
it
follows from Proposition 5.7 that, for kl
>
1, cp;(x) is also
an eigenfunction of
A
for eigenvalue (p2
+
i).
A
similar argu-
ment shows that <P;(x) is an eigenfunction of
A
for eigenvalue
(p2
+
a).
Obviously b-,(x) and O',(x) are also eigenfunctions of
A
for eigenvalue (p2
+
a).
Proof. Combining the contiguous relations (Andrews et al., 1999, (3.7.9))
(3.7.10)) (3.7.13))) gives
From this relation we find that
e-2~~
I?
(1
-
kl
+
it
+
ix)
I?
(kl
+
ix
+
it)
x
3~2
(
k2
-
ix, k2
-
k1
+
4
+
ip, k2
-
k1
+
4
-
ip
2k2, k2
-
kl
+
it
+
1
;
1)
is an eigenfunction of
A
for eigenvalue p2
+
$.
And then, since
p(z)
is
i-periodic, cp,(x) is also an eigenfunction for eigenvalue
p2
+
$.
Since
vp(x) must be analytic in
S,,
the condition kl
>
1
is needed for absolute
convergence of the 3F2-series at the point x
+
i.
Denote

Continuous Hahn functions
257
From contiguous relations (Andrews et al.,
1999, (3.7.9), (3.7.10), (3.7.13))
we find
[(d
-
l)(e
-
1)F-(a+)
-
(b-
l)(c- 1)F]
-
(a
-
l)(d
+
e
-
a
-
b
-
c)F
From this we see that
I'
(1
-
k2
+
ix)
r(l+
2ip)F (1
-
k1+ ix
+
it)
@PW
=
r
(&
+
it
+
ip)
I?
(kl
+
g
+
ip
+
ix)
r
(g
-
kl
+
iz
+
ip)
x
e-2~xp(x) 3F2
3
-
it
+
ip,
1
-
k2
+
ix, k2
+
ix
+
ix
+
ip,
-
kl
+
ip
+
ix
;
1)
,
(5.6)
is another eigenfunction of
A
with eigenvalue
p2
+
$.
The
3F2
series
converges absolutely if
R
(&
+
ip
+
it)
>
0,
so absolute convergence does
not depend on
kl.
Using (Andrews et al.,
1999,
Cor.
3.3.5)
this can
be written
as
(5.5),
and for this expression the condition
kl
>
1
is
needed.
0
The function
cpp(x)
can be expanded in terms of
ap(x)
and
@-p(x).
Proposition
5.9.
where
Proof.
This follows from (Bailey,
1972,
p.
15(2))
Here idem@;
c)
after
an
expression means that the expression is repeated
with
b
and
c
interchanged.
0
In the next subsection we consider the Wronskians
[yp,
yo]
(9)
and
[cp;,
ya] (y)
for
y
+
f
oo,
so we need the asymptotic behaviour of
yp.
We find this from Proposition
5.9
and the asymptotic behaviour of
@,.

258
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
Lemma
5.10.
Let
kl
>
1,
p
E
@
and
-1
5
y
5
1.
For
x
+
fa
where
+
(k2
-
ki
+
f
+
ip)
(4
-
kl
-
k2
+
ip)
(f
-
it
+
ip)
f
+ip
3
B(p)
=
2kl
+
2k2
-
1
+
2ip.
Proof.
This follows from (5.5) and the asymptotic formula for the ratio
of two I?-functions (Olver, 1974, $4.5)
The first part of the expression for A(p) is obtained from
the second part comes from the second term in the hypergeometric series.
0
The asymptotic behaviour of the i-periodic function p(x) is also needed;
e-irkl
I-,
ePTt
+
0
(e2=l)
,
z
+
-a,

Continuous Hahn functions
einkl
e-in(kl
-2y)
p*(x
+
iy)
=
-
e-7rt
-
en(2~+t)
2ni
27ri
5.3
Continuous spectrum
We determine the spectrum of the difference operator
A.
In this
subsection we consider the case where the spectrum only consists of
a continuous part.
Since
we find from Proposition
5.10
that
So cPp(x) is an element of L2(R, w(x)dx) for Q(p)
<
0.
This shows that
it is possible to give eigenfunctions of
A
for complex eigenvalues. We
only consider eigenfunctions which are even in p, and in that case all
eigenvalues of
A
are real.
First we consider the continuous spectrum of
A.
We show that
[a,
00)
is contained in the continuous spectrum. Assume that p is real and that
the c-function in Proposition
5.9
does not have zeros, or, equivalently,
assume that kl
+
k2
2
and k2
-
kl
>
-4.
Since we only consider
even functions in p, we may assume p
2
0.
We use Proposition
5.3
to
calculate the truncated inner product of two eigenfunctions. This gives
for kl
>
1
and p
#
a
Multiplying both sides with an arbitrary function
f
(p) and integrating
over p from
0
to
00,
gives

260
THEORY AND APPLICATIONS OF SPECIAL FUNCTIONS
The function
f
(p) must satisfy some conditions, which we shall deter-
mine later on. We take limits
N,
M
-t
co
on both sides. To determine
the limits of the Wronskians, the following lemma is used.
Lemma
5.11.
Let
kl, k2
>
1
and
p,
a
>
0.
For
x
-t
f
co
where
Proof.
From Lemma 5.10 we find for 0
<
y
<
1
and
x
-+
co
Gp (x
+
iy)
Gz
(x
+
iy
-
i)
-
Gp
(x
+
iy
-
i)
@;
(x
+
iy
)
- -
e2i(p-4i(py+4iny-4cpz
1-2kl-2kz
1x1 lP(x) 12(ix)-i~(-ix)iu
Using the asymptotic behaviour of
p(x)
and Lemma 5.4, we find the
asymptotic behaviour of the integrand of the Wronskian. Note that
this is independent of
y.
In a similar way we find the same asymptotic
behaviour of the integrand for
x
-t
-a.
Now the lemma follows from
writing the Wronskian as
and applying dominated convergence.
0
Proposition
5.12.
Let
a
>
0,
and
let
f
be a continuous function sat-
isfying
)
P+W, &>0,
f
(PI
=
p
-+
0,
6
>
0,
then
00

Continuous Hahn functions
where
r(k2
-
kl
+
$
+
ia)r(kl
+
k2
-
+
ia)
r(2k2)r(k2
-
kl
+
it
+
l)r(2ia)
Proof.
Let
kl, k2
>
1.
We use
(5.10)
to calculate
From the c-function expansion, see Proposition
5.9,
we obtain
Then
(5.9)
and Lemma
5.11
give, for
N
-t
oo,
From
(5.10)
we find
where
