Карасева Р.Б.Высшая математика.Ч1.Электронное учебное пособие

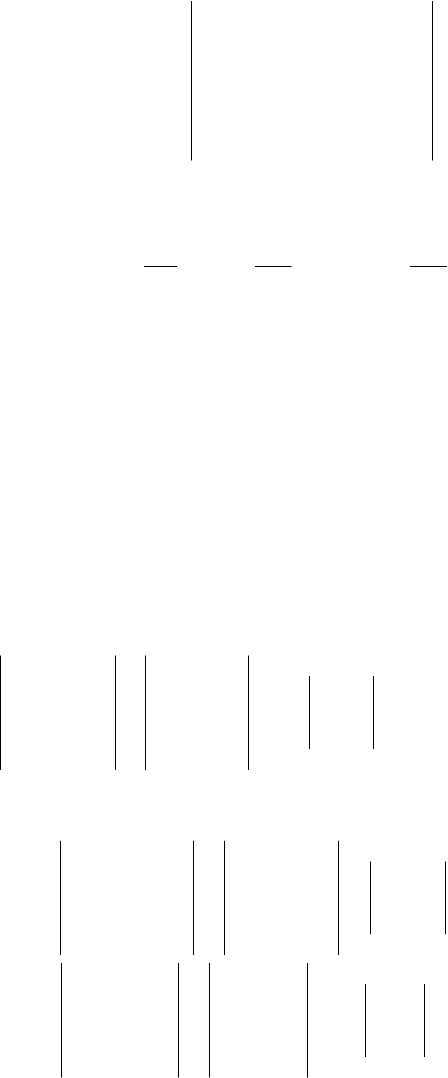
В случае, когда число неизвестных совпадает с числом уравнений (т.е. nm

=

)

и определитель системы отличен от нуля

0det

21

22221

11211

≠==∆

nmmm

n

aaa

A

L

LLLL

L

,

система линейных уравнений (1) имеет единственное решение, определяемое

по формулам Крамера:

∆

=

1

a

,

,,

2

K

∆

=a

∆

=

n

a

,

где

i∆

– определитель, который получается из определителя системы, если в

нем

i-й столбец заменить столбцом свободных членов

(

)

ni ,,2,1 K

=

.

Пример 1.

Решить систему:

⎪

⎩

⎪

⎨

⎧

−=+−

=+−

=

+

.12

;02

;1

zyx

Находим определитель системы:

()

0549

32

23

1

302

203

111

211

112

111

≠−=−−=−==

−

−=∆

,

значит можно систему решить по формулам Крамера.

Считаем вспомогательные определители:

3

30

11

310

110

111

211

110

111

−=

−

=

−

−=

−−

−=∆

x

;

()

426

32

12

1

302

102

111

211

102

111

−=−−=−==

−

=∆

y

;

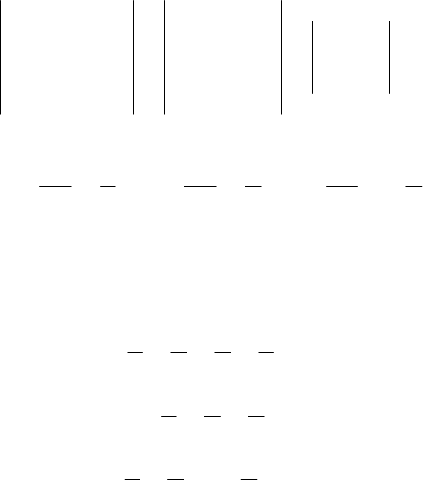
2

02

12

002

012

111

012

111

=

−

=−=

−−

−=∆

z

.

Решение получаем по формулам Крамера:

;

5

3

=

∆

=

x

x ;

5

4

=

∆

=

y

5

2

−=

∆

=

z

z .

Правильность решения системы проверяется подстановкой решения в систе-

му.

Проверка:

⎪

⎩

⎪

⎨

⎧

−=⋅−−

=−−⋅

==−+

.1

5

2

5

4

5

3

;0

5

2

5

4

5

3

2

;1

5

2

5

4

5

3

Матричный способ

Предполагаем, что число уравнений совпадает с числом неизвестных и

что определитель системы отличен от нуля, то есть является крамеровской.

Заменим исходную систему (1) эквивалентным ей матричным уравнением:

,

B

AX

=

(2)

где

−

⎟

⎠

⎞

⎜

⎝

⎛

=

n

x

X

L

2

1

матрица-столбец, составленная из переменных.

Поскольку матрица

A

– невырожденная, значит, существует ей обрат-

ная

1−

A

. Умножим обе части уравнения (2) на

1

−

A

слева:

(

)

BAAXA

11

−

=

.

Имеем:

(

)

;

11

BAXAA

−

=

;

1

BAEX

−

=

.

1

B

A

X

−

=

Пример 2.

Решить систему

⎪

⎩

⎪

⎨

⎧

−=++

=++

=

−

.122

;023

;52

zyx

011

221

213

121

≠=

−

=∆

.

⎟

⎠

⎞

⎜

⎝

⎛

−

=

⎟

⎠

⎞

⎜

⎝

⎛

−

⋅

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−

=

⎟

⎠

⎞

⎜

⎝

⎛

−

=

⎟

⎠

⎞

⎜

⎝

⎛

−

13

15

7

1

0

5

745

534

322

1

0

5

1

A

z

y

x

,

т.е.

;7−=

x

;15−=y

.18=z

Задачи для самостоятельного решения

1. Получить условие, при котором три плоскости пересекаются в одной точке.

2. Решить системы по формулам Крамера:

а)

⎪

⎩

⎪

⎨

⎧

=+−

=−+

=

−

;11423

;11243

;42

zyx

б)

⎪

⎩

⎪

⎨

⎧

−=++

−=+−

−=

−

;2424

;422

;12

321

xxx

в)

⎪

⎩

⎪

⎨

⎧

=++

=

+

;1132

;132

;523

zyx

г)

⎪

⎩

⎪

⎨

⎧

=+−

=++

=

+

;103

;2925

;3142

zyx

д)

⎪

⎩

⎪

⎨

⎧

−=−++

−=−−+

−=−−−

=+++

;432

;632

;423

;132

tzyx

е)

⎪

⎩

⎪

⎨

⎧

−=++−

=−−+

=−−−

=−

+

.8232

;4223

;8322

;6232

tzyx

3. Решить системы матричным способом:

а)

⎪

⎩

⎪

⎨

⎧

=−+

=+−

;23

;032

;542

zyx

б)

⎪

⎩

⎪

⎨

⎧

=+−

=++

=

+

;523

;732

;3

zyx

в)

⎪

⎩

⎪

⎨

⎧

=+−

−=++

=

+

−

;1

;135

;342

zyx

г)

⎪

⎩

⎪

⎨

⎧

=++

=

+

.522

;1435

;22

zyx

4. Показать, что многочлен степени n вполне определяется его значениями

при

1+n

значениях неизвестного. Или показать, что для любых различных

между собой чисел

n

xxxx ,,,,

210

K и любых

n

yyy K,,

10

существует и при-

том только один многочлен

(

)

xf

степени

n

, для которого

()

,

ii

yxf

=

ni ,,2,1,0 K=

. Какой геометрический смысл имеет это утверждение?

5. Найти квадратный многочлен

(

)

xf , зная, что

(

)

(

)()

.32,91,11

−

=

−

=

fff

6. Найти многочлен 3 степени

(

)

xfy

=

, для которого

() ()

,41,01

=

=− ff

() ()

.163,32 == ff

7. Найти многочлен

()

xfy = 3-й степени, график которого проходит через

точки

()

1,0 ;

()

1,1 − ;

()

5,2 ;

()

37,3 .

Ответы

2. а) ;3=

x

;1=y

;1

=

z б)

;1

1

=x

;2

2

=

x

2

3

−

=

x

;

в)

;2=

x

;2−=y

3=z ; г)

;3

=

x

;4

=

y

5

=

z ;

д)

;1

−=

x

;1

−=y

;0=z

;1=

t

е)

;1

=

x

;2

=

y

;1

−

=

z

.2

−

=

t

3. а)

;5=

x

;2=y

;

2

3

+=z

б)

;1

=

x

;0

=

y

;2

=

z

в)

;2=

x

;0=y

;1−

=

z

г)

;2

=

x

;5

−

=

y

.3

=

z

5.

()

35

2

+−= xxxf

.

6.

()

752

23

+−= xxxf

.

7. 153

23

+−= xxy .

§5. Ранг матрицы

В прямоугольной матрице выделим

k

произвольных строк и

k

произ-

вольных столбцов

(

)

., nkmk ≤≤

⎟

⎠

⎞

⎜

⎝

⎛

=

nmmm

n

aaa

A

L

LLLL

L

21

22221

11211

.

Определитель

k

-го порядка, составленный из элементов матрицы

A

,

расположенных на пересечении выделенных строк и столбцов, называется

минором k-го порядка матрицы

A. Матрица A имеет

k

n

k

m

CC ⋅

миноров k -го

порядка, где

−

k

m

C

число сочетаний по k элементов из

m

,

()

!!

!

kmk

m

C

k

m

−

=

.

Рангом матрицы А называется наибольший порядок минора этой мат-

рицы, отличный от нуля. Обозначают

(

)

Ar ,

(

)

Arang

. Если все элементы мат-

рицы равны нулю, то ранг этой матрицы принимают равным нулю.

Всякий отличный от нуля минор матрицы, порядок которого равен ран-

гу этой матрицы, называется

базисным минором матрицы. Строки и столб-

цы, на пересечении которых стоит базисный минор, называют

базисными

строками и столбцами.

Т е о р е м а. Пусть в матрице

A

имеется минор

M

– порядка

r

, от-

личный от нуля, а всякий минор порядка

1

+

r

, включающий все элементы

минора

M

(окаймляющий минор), равен нулю, тогда ранг матрицы

A

ра-

вен

r

.

Эта теорема дает способ нахождения минора ранга матрицы

A

. Нахо-

дим минор матрицы

A

порядка

r

, отличный от нуля. Затем вычисляем толь-

ко миноры порядка

1+

r

, окаймляющие этот минор. Если все они равны ну-

лю, то ранг матрицы

A равен

r

.

Ещё один менее трудоемкий способ нахождения ранга матрицы осно-

ван на применении

элементарных преобразований матрицы, не изменяю-

щих ранга матрицы:

1) перестановка строк матрицы;

2) вычеркивание строки, все элементы которой равны нулю;

3) умножение какой-либо строки на число, отличное от нуля;

4) прибавление к элементам одной строки соответствующих элементов

другой строки;

5) те же операции со столбцами.

Любую матрицу можно элементарными преобразованиями привести к

диагональной форме. Тогда ранг матрицы равен числу отличных от нуля эле-

ментов диагонали.

Найти ранг матрицы:

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−

=

274

812

153

242

121

A

I способ

Выделяем в матрице

A

минор второго порядка, отличный от нуля:

.021210

53

42

1

≠=+−=

−

=M

Вычисляем окаймляющие его миноры третьего порядка:

;0

153

242

121

2

=−−−=M ;0

812

153

242

3

=

−

=M .0

274

153

242

4

=

−−

−

=M

Все окаймляющие миноры равны нулю, значит, ранг матрицы

A

равен 2.

II способ (линейные преобразования)

~

014

052

013

001

~

052

013

001

~

214

213

002

001

~

274

153

242

121

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

⎟

⎠

⎞

⎜

⎝

⎛

−−−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

10

01

~

000

010

001

~

050

010

001

~

010

050

010

001

~

.

Ранг

A

равен 2:

()

2=Arang

.

Часто эти два способа комбинируют. Элементарными преобразования-

ми матрицу

A

можно привести к такому виду, из которого ранг матрицы лег-

ко находится:

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

−−

−

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−

24

102

23

02

01

~

214

1052

213

002

001

~

274

812

153

242

121

.

В последней матрице легко

выделить минор второго порядка, отличный от

нуля.

Т е о р е м а о б а з и с н о м м и н о р е. В произвольной матрице ка-

ждый столбец является линейной комбинацией базисных столбцов, а каждая

строка – линейной комбинацией базисных строк.

С л е д с т в и е. Если A – квадратная матрица и 0det =

A

, то по край-

ней мере один из столбцов – линейная комбинация остальных столбцов, а

также одна из строк – линейная комбинация остальных строк.

Т е о р е м а о р а н г е м а т р и ц ы. Ранг матрицы

A

равен макси-

мальному числу линейно независимых столбцов в этой матрице (аналогичное

утверждение верно для строк).

С л е д с т в и е. Максимальное число линейно независимых строк в

матрице равно максимальному числу линейно независимых столбцов в этой

матрице.

Задачи для самостоятельного решения

1. Чему равен ранг диагональной матрицы порядка

n

?

2. Сколько матриц

k

-го порядка можно составить из матрицы, имеющей

m

строк и

n

столбцов?

3. Составить матрицу, ранг которой равен

а) 2;

б) 3.

4. Доказать, что ранг суммы двух матриц не превосходит суммы рангов сла-

гающих матриц.

5. Как может измениться ранг матрицы, если приписать к ней

а) 1 столбец;

б) 2 строки.

6. Когда вычеркивание одной строки (столбца) матрицы не изменяет её ран-

га?

7. Найти ранг матрицы

A

методом окаймления миноров.

а) ;

1977

7115

4312

1531

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−

б) ;

14157

70531

43235

52313

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−

в)

.

64168

52134

72834

24768

32534

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

8. Найти значения

λ

, при которых матрица имеет наименьший ранг

⎟

⎠

⎞

⎜

⎝

⎛

3422

31771

1104

4113

λ

.

Чему равен ранг при найденных

λ

и чему он равен при других

λ

?

9. Чему равен ранг матрицы при различных значениях

λ

,

⎟

⎠

⎞

⎜

⎝

⎛

03

654

321

λ

?

10. Вычислить ранг матрицы, применяя элементарные преобразования:

а)

;

11010

01100

00110

00011

00101

⎟

⎠

⎞

⎜

⎝

⎛

б)

;

01010

12012

01010

20202

⎟

⎠

⎞

⎜

⎝

⎛

в)

⎟

⎠

⎞

⎜

⎝

⎛

−

1134

2431

0213

1312

г)

;

1111

4321

5111

1411

1131

1112

⎟

⎠

⎞

⎜

⎝

⎛

д)

;

171810

784

371

⎟

⎠

⎞

⎜

⎝

⎛

е)

;

1134

111

512

201

⎟

⎠

⎞

⎜

⎝

⎛

−

ж)

;

5131

5154

3112

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−

з) ;

213

312

521

⎟

⎠

⎞

⎜

⎝

⎛

−

и) .

243

222

531

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

11. Найти все значения

λ

, при которых вектор b линейно выражается через

векторы

321

,, aaa .

а)

{}

;5,3,2

1

=a

{}

;,2,7

λ

−=b

{

}

;1,6,1

2

−=a

{

}

;8,7,3

3

=a

б)

{}

;3,4,4

1

=a

{}

;,9,5

λ

=b

{

}

;1,2,7

2

=a

{

}

.6,1,4

3

=a

12. Найти все максимальные линейно независимые подсистемы векторов:

{}

;2,3,1,4

1

−−=a

{

}

;2,4,1,3

2

−−=a

{}

;4,6,2,8

3

−−=a

{

}

.4,8,2,6

4

−−=a

Ответы

1.

k

n

k

m

CС ⋅

5. а) не изменится или увеличится на 1;

б) либо не изменится, либо увеличится на 1 или на 2.

6. Тогда и только тогда, когда вычеркнутая строка (столбец) линейно выража-

ется через остальные строки (столбцы).

7. а) 3; б) 3; в) 2.

8. При

0=λ

ранг матрицы равен 2; при

0

=

λ

ранг равен 3.

9. При 3=λ ранг равен 2; При 3

≠

λ

ранг равен 3.

10. а) 5; б) 3; в) 2; г) 4; д) 2; е) 2; ж) 3; з) 3; и) 2.

11. а) 15=

λ

; −

λ

любое.

12. Таких систем четыре: 1) ;,

31

aa

r

2) ;,

41

aa

r

3) ;,

32

aa

r

4)

42

, aa

r

.

§6. Однородные системы

Рассмотрим однородную систему

(

)

0

321

==

=

n

bbbb K линей-

ных уравнений:

⎪

⎩

⎪

⎨

⎧

=++

=+++

.0

;0

2211

1212111

nnmmm

nn

xaxaxa

K

LLLLLLLLLLLL

K

Такая система всегда совместна, т.к. всегда имеет нулевое (тривиальное)

решение:

0

321

=

==

=

n

xxxx K

. Чтобы однородная система имела не-

нулевые решения, необходимо и достаточно, чтобы ранг

r

её матрицы был

меньше

n.

⎪

⎩

⎪

⎨

⎧

=++

=+−

=

+

−

,0

;02

;022

zyx

.3

=

n

(

)

.2 nAr

<

=

Минор второго порядка, отличный от нуля, расположен в левом углу мат-

рицы, т.е. третье уравнение – следствие первых двух.

Решаем систему

⎩

⎨

⎧

=+−

=

+−

.02

;022

zyx

или

⎩

⎨

⎧

−=−

−

=

−

.2

;2

zyx

Отсюда по формулам Крамера получаем решение (

z

– свободная пе-

ременная): 0; =−= yz

x

.

В случае nm

=

однородная система имеет единственное нулевое ре-

шение при условии 0de

t

≠

A

. Если 0de

t

=

A

, то система имеет бесчислен-

ное множество ненулевых решений.

⎪

⎩

⎪

⎨

⎧

=−+

=+−

=

+

−

,0

;0

;032

zyx

.3

=

nm

.02

111

321

det ≠=−

−

=A

Система имеет только тривиальное решение .0=

=

zy

x

⎟

⎠

⎞

⎜

⎝

⎛

−

=

111

121

212

A

Карасева Р.Б.Высшая математика.Ч1.Электронное учебное пособие

Подождите немного. Документ загружается.