Карасева Р.Б.Высшая математика.Ч1.Электронное учебное пособие

⎪

⎩

⎪

⎨

⎧

=−+

=

−

+

,0822

;01233

;04

zyx

.3

=

mn

.0

822

1233

411

det =

−

=A

Очевидно, что в системе только одно независимое уравнение:

04 =−+ zy

x

(т.к.

()

1=Ar ).

Объявляем y и

z − свободными переменными и получаем множест-

во решений: .4zy

x

+−=

Множество решений однородной системы обладает двумя важными

свойствами. Если столбцы

1

x и

2

x – решения однородной системы, то их

сумма

21

xx +

– также решение однородной системы.

Произведение решения однородной системы на любое число являет-

ся решением той же системы.

Задачи для самостоятельного решения

1. Исследовать и найти все решения системы:

а)

⎪

⎩

⎪

⎨

⎧

=++

=+−

=

+

;034

;04

;05210

zyx

б)

⎪

⎩

⎪

⎨

⎧

=−−

=−+

=

+

;0352

;027

;046

zyx

в)

⎪

⎩

⎪

⎨

⎧

+++

=++−

=−+

;02

;025

;02

zyx

г)

⎪

⎩

⎪

⎨

⎧

=++−

=+−+

=−+−

=+−+

;0327

;01613114

;02332

;07543

4321

xxxx

д)

⎪

⎩

⎪

⎨

⎧

=−+++

=+++

−=−+++

=++++

;123345

;23622

;2323

;7

54321

5432

54321

xxxxx

xxxx

xxxxx

е)

⎩

⎨

⎧

=+−

;0392

;03

zyx

ж)

⎩

⎨

⎧

=++

=

+

−

;0

zyx

λ

з)

⎩

⎨

⎧

=+−

=−+

;0523

;032

zyx

и)

⎩

⎨

⎧

=+−

=

−

+

;053

;02

zyx

к)

⎪

⎩

⎪

⎨

⎧

=−+−−

=+−−+

=−++−

;023

;05557

;02

54321

54322

54321

xxxxx

л)

⎪

⎩

⎪

⎨

⎧

=+−+−

=−+−−

=−+−+

=+−+−

.02252

;0223

;0322

;02

54321

xxxxx

2. При каких значениях параметра система имеет ненулевые решения?

а)

⎪

⎩

⎪

⎨

⎧

=+

=++

=

+

;0

;043

;02

yx

zyx

zyax

б)

(

)

()

⎪

⎩

⎪

⎨

⎧

=+++

=+−

=

+

−

+

.014

;01

;023

zyax

zxa

zyax

Ответы

1. а) ;

7

10

xy = ;

7

18

xz −=

;

R

x

∈

б) ;0

=

zy

x

;47

−

=

∆

в) ;0=== zy

x

;24−=

∆

г) ;

17

133

43

1

xx

x

−

= ;

17

2019

43

2

xx

x

−

=

д) ;516

5431

xxxx +

+

+−= ;62223

5432

xxxx

−

=

е) ;0=

x

;

3

z

y = ;

R

z∈ ж) ;z

x

−

=

(

)

;1 zky

−

=

;

R

z

∈

з) ;

2

7

−=x ;

4

7

zy = ;

R

z∈ и) ;

4

3

yx = ;

4

11

yz = ;

R

y

∈

к) ;0

321

=== xxx ;

54

xx =

л) ;

8

74

54

1

xx

x

+−

=

;

8

54

2

xx

x

+

−

=

8

54

3

xx

x

−

= .

2. а) ;

4

9

=a

б) .31 ±−

=

a

§7. Системы линейных уравнений: общий случай

Рассмотрим систему

m линейных уравнений с n переменными.

⎪

⎩

⎪

⎨

⎧

=+++

.

;

2211

11212111

mnnmmm

nn

bxaxaxa

K

LLLLLLLLLLLLL

K

Поскольку каждый минор матрицы

A

является минором расширен-

ной матрицы *

A

, но не наоборот, то

)(*)(

A

r

A

r

≥

Критерий совместности системы линейных уравнений (теорема

Кронекера-Капелли

): для совместности системы линейных уравнений

необходимо и достаточно, чтобы ранг матрицы системы был равен рангу

расширенной матрицы системы:

(

)

(

)

.*ArAr

=

Совместная система называется

определенной, если она имеет толь-

ко одно решение, и

неопределенной, если она имеет больше одного реше-

ния.

Пусть ранг матрицы

A

равен

r

, и определитель

r

-го порядка, от-

личный от нуля (базисный минор), расположен в левом верхнем углу мат-

рицы

A

(это всегда можно сделать простой перестановкой уравнений в

системе). Тогда первые

r

строк матрицы *

A

линейно независимы, а ос-

тальные

()

rm − строки линейно выражаются через них. Т.е. первые

r

уравнений системы линейно независимы, а остальные

(

)

rm − уравнений

являются их следствиями. Достаточно решить лишь первые

r

независи-

мых уравнений, т.к. остальные уравнения будут этим решениям удовле-

творять.

Возможны два случая:

1.

() ( )

nrArAr === *. (Ранг равен числу неизвестных).

Систему из первых

r

уравнений можно решить по формулам Краме-

ра. Система

m линейных уравнений с n неизвестными совместна, опреде-

лена, имеет единственное решение.

⇒

⎪

⎩

⎪

⎨

⎧

=+−

=−−−

=+−

=

−

+

,3

;02

;13

;22

zyx

.3

=

n

;

111

121

311

121

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−

−

=A

⎟

⎠

⎞

⎜

⎝

⎛

−−−

−

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−

−

=

0000

0121

1311

2121

~

3111

0121

1311

2121

*A

,

т.е. четвертое уравнение системы – линейная комбинация первых трех.

Минор третьего порядка, расположенный в верхнем левом углу матрицы,

отличен от нуля:

()

.3*,6

121

311

121

=⇒=

−−−

−

=∆ Ar

Этот определитель состоит из строк матрицы

A

,

(

)

3=Ar .

Получили:

() ( )

nArAr

=

= 3*. Система имеет единственное реше-

ние, это решение находится по формулам Крамера из системы (4-м урав-

нением можно пренебречь):

⎪

⎩

⎪

⎨

⎧

⇒

=−−−

=+−

=

−

+

.02

;13

;22

zyx

.1

;1

;3

−

=

−=

=

z

y

x

2. .n

r

<

Возьмем первые

r

уравнений системы (1), первые

r

переменных на-

зовем

основными, остальные

r

n

−

переменных назовем свободными.

Слагаемые, содержащие свободные переменные, перенесем в правые час-

ти:

⎪

⎩

⎪

⎨

⎧

−−=+++

−−−=+++

++

.

;

11222121

1111121212111

nnrrrrrrrr

nnrrr

xaxabxaxaxa

KK

LLLLLLLLLLLLL

KK

(3)

Решая систему (3) по формулам Крамера, мы получим формулы, вы-

ражающие основные переменные

r

xxx ,,,

21

K через свободные перемен-

ные

nrr

xxx ,,,

21

K

++

. Придавая свободным переменным произвольные

значения, получаем бесконечное множество всех решений системы.

Пример

Решить систему

⎪

⎩

⎪

⎨

⎧

=−−+

=+−+−−

=−+−+

=+−−+

.1234

;15932

;02

;123

4321

54321

xxxx

xxxxx

()

.2*

101234

159321

012111

111123

* =⇒

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−

−−

−

= ArA

()

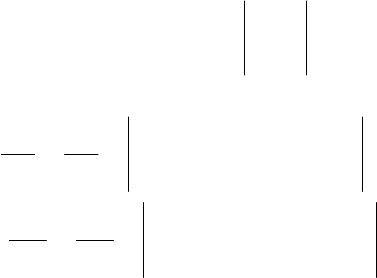
.2

01234

59321

12111

11123

=⇒

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−

−−

−

= ArA

()

(

)

.52*

=

<

=

nArAR

Минор второго порядка, отличный от нуля, расположен в левом

верхнем углу матрицы

*

A

. Составим подсистему, состоящую из первых

двух уравнений (остальные уравнения – их линейная комбинация), и ре-

шим её относительно переменных

21

, xx . Остальные

(

)

325 =−=

−

rn пе-

ременные

543

,, xxx считаем свободным.

⎩

⎨

⎧

+−=+

−++=+

;2

;123

54321

xxxxx

.1

11

23

==∆

Решая эту систему по формулам Крамера получим:

;351

12

21

1

543

11

1

xxx

x −+−=

+−

−++

=

∆

=

∆

=

.4721

21

13

1

543

22

2

xxx

x +−+−=

+−

−++

=

∆

=

∆

=

При разных значениях

543

,, xxx , мы получим бесконечно много ре-

шений системы.

З а м е ч а н и е 1. При выборе другого базисного минора мы имели

бы другие формулы, описывающие то же множество решений системы (3).

Например, если в примере за базисный взять минор 2-го порядка, стоящий

в правом нижнем углу, основными переменными будут

4

x

и

5

x

а свобод-

ными

−

321

,, xxx

.

З а м е ч а н и е 2. Если в исследуемой системе число уравнений

совпадает с числом неизвестных, 0de

t

=

A

, то

(

)

nAr

<

. В случае, когда

() ( )

*ArAr ≠ система несовместна.

Задачи для самостоятельного решения

1. Исследовать системы уравнений. В случае совместности системы найти

все её решения:

а)

⎪

⎩

⎪

⎨

⎧

−=+−

=−+

−=++

;753

;11435

;4

zyx

б)

⎪

⎩

⎪

⎨

⎧

=+−

=−+

=

+

−

;132

;2423

;4225

zyx

в)

⎪

⎩

⎪

⎨

⎧

=+−

=++−

=

−

+

;3171112

;243

;12

zyx

г)

⎪

⎩

⎪

⎨

⎧

=+−

−=+−

=

+

−

;547

;435

;923

zyx

д)

⎪

⎩

⎪

⎨

⎧

=++

=+−

=++

;62

;5

;4

zyx

е)

⎪

⎩

⎪

⎨

⎧

=++−

−=−+−

=

+

−

;552

;12

4321

xxxx

ж)

⎪

⎩

⎪

⎨

⎧

=−+

−=++

=++

=

+

;14332

;75

;53

;22

zyx

з)

⎪

⎩

⎪

⎨

⎧

−=+−+

−=+−

=−−

=−+−

;65222

;33

;232

;12

4321

431

421

4321

xxxx

xxx

xxxx

и)

⎩

⎨

⎧

=++−−

=+++

;1

;5324

4321

xxxx

к)

⎪

⎩

⎪

⎨

⎧

−=++−

=−+

−=+−

=−+−

;337

;133

;3

;4432

431

421

432

4321

xxx

xxxx

л)

⎪

⎩

⎪

⎨

⎧

−=+−+−

=+−+−

=−+−+

=+−+−

.11177142

;1755104

;122

54321

xxxxx

2.

Подобрать

λ

так, чтобы система уравнений имела решение

⎪

⎩

⎪

⎨

⎧

=+−+

=−−+

=

+

−

.242

;11472

;12

4321

xxxx

λ

3. При каких значениях а система уравнений

⎪

⎩

⎪

⎨

⎧

−=++

=+−

=

+

−

.12

;23

;1985

zyx

azyx

zyx

а) имеет единственное решение;

б) не имеет решений.

4. Исследовать систему при различных значениях

λ

,,

21

:

а)

⎪

⎩

⎪

⎨

⎧

=++

=

+

;42

;3

;4

2

zyx

λ

б)

⎪

⎩

⎪

⎨

⎧

=++

=

+

.1

;

2

zyx

λ

λλ

λ

Ответы

1. а) ;1=

x

;2−=y ;3−=z б) ;

8

113

;

4

3

−

=

+

=

z

y

z

x

в) несовместна; г) несовместна;

д)

;

2

5

=x

;

2

1

−=y

;2=

z

e) ;1;2

4123

=

−

=

xxxx

ж) ;1=

x

;2=y ;2−=

z

з) ;

3

4

;

3

5

;2;0

4321

−==== xxxx

и) ;

3

257

;

3

522

13

4

13

2

xx

x

xx

x

−

=

−

=

где

31

, xx

– любые действительные числа;

к) ;26;3;8

43421

xxxxx

+

=+=−=

л)

6

5331

;

3

2

543

2

5

1

xxx

x

+

−

+

=

+

=

.

2. 5=λ .

3. а) ;3≠a б) 3=a .

4. а) Если

()

01

12

≠−λλ

,

()

;

1

12

2

−λλ

−

λ

=x ;

1

2

λ

=

y

()

1

142

12

221

−λλ

+λ

−

λ

=z .

Если 1

1

=λ ,

2

1

2

=λ , решения зависят от одного параметра. В остальных

случаях система решений не имеет.

б) Если

()( )

021 ≠

+

λ−λ , ;

2

1

+λ

+

λ

−=x ;

2

1

+λ

=y

(

)

2

1

2

+λ

=z .

Если 1=λ , система имеет решения, зависящие от двух параметров. Если

1−=λ , система решений не имеет.

§8. Метод Гаусса

Метод Гаусса (метод последовательного исключения неизвест-

ных) – метод нахождения множества решений системы линейных уравне-

ний – заключается в приведении расширенной матрицы системы

⎟

⎠

⎞

⎜

⎝

⎛

=

mnmmm

n

baaa

A

L

LLLLL

L

21

222221

111211

*

с помощью элементарных преобразований, производимых только над

строками этой матрицы к трапецевидному

⎟

⎠

⎞

⎜

⎝

⎛

′

′′

=

mmn

n

mm

m

b

a

aa

aaa

A

L

KL

LLL

LL

2

1

2

1

222

11211

00

0

~

или близкому к нему виду.

Система уравнений, соответствующая матрице

A

~

, эквивалентна ис-

ходной, её решение несложно.

После выполнения элементарных преобразований получается матри-

ца одного из трех видов:

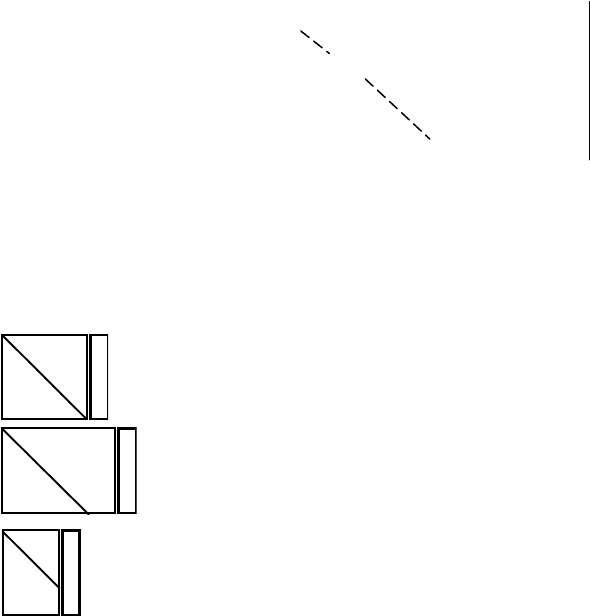
а)

0

⇒ система имеет единственное решение (совместна)

б)

0

⇒ система имеет множество решений (совместна)

в)

0

0=

1

⇒ система противоречива, решений не имеет (несовместна)

Пример 1.

⎪

⎩

⎪

⎨

⎧

=−+⋅

=⋅+−

=⋅+−⋅

=

−

+

.124

;03

;832

;4

zyx

Выписываем расширенную матрицу и делаем элементарные преоб-

разования только со строками:

()()()

()

~

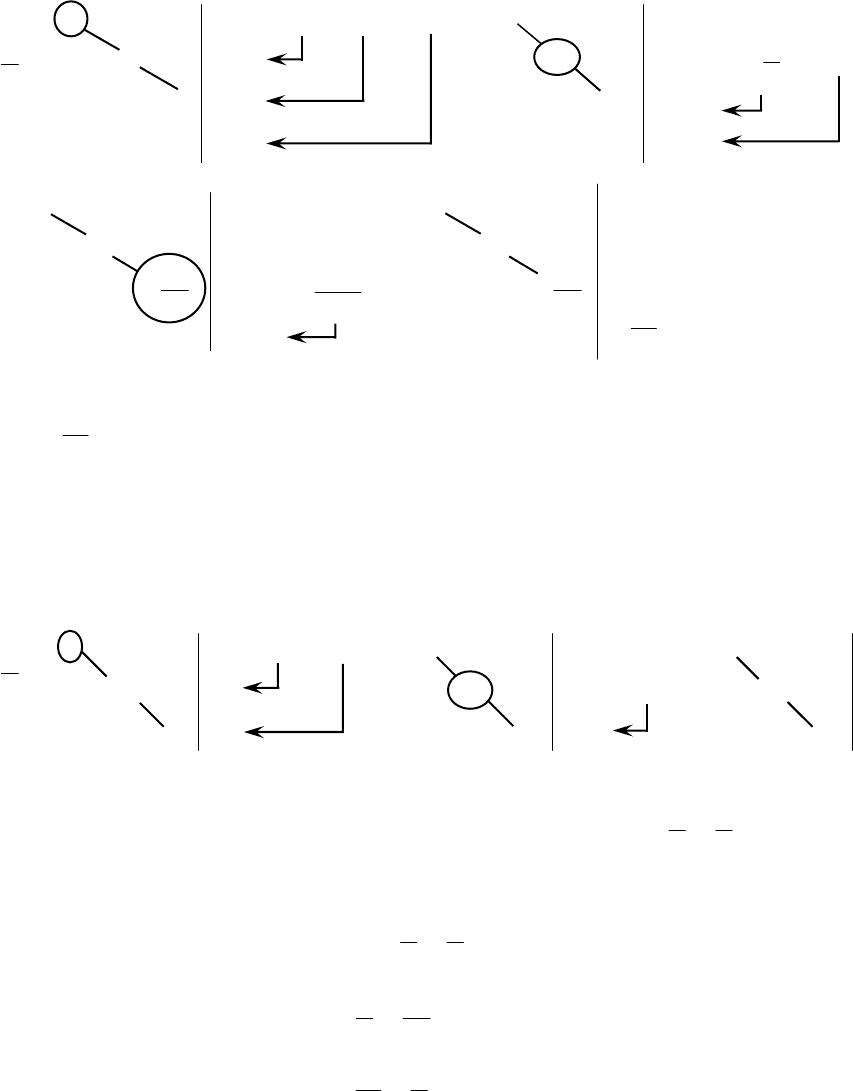
1

3

2

4

0

4

330

220

430

111

~

41 2

12

0

8

4

114

311

312

111

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−

−−−−

⎟

⎠

⎞

⎜

⎝

⎛

−

−−

−

=A

.

2

11

4

0

4

000

3

16

00

530

111

~

16

32

4

0

4

200

3

16

00

530

111

~

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

−

Система приведена к трапециевидному виду. Последнее уравнение:

2

11

0 −=

− противоречие ⇒ система несовместна (решений нет)

Пример 2.

⎪

⎩

⎪

⎨

⎧

=+⋅+⋅

=⋅+−⋅

=

−

⋅

+

.523

;322

;23

zyx

()()

()

.

0

1

2

000

470

131

~1

1

2

470

131

~

32

5

3

2

123

212

131

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−

⎟

⎠

⎞

⎜

⎝

⎛

−

=A

Нулевую строку отбрасываем, выписываем систему:

.

7

4

7

1

417

;147

;23

zyzy

zy

zyx

⋅+=⇒⋅−−=⋅−⇒

⎩

⎨

⎧

−=⋅+⋅−

=−

⋅

+

Подставляем в первое уравнение:

;2

7

4

7

1

3 =−

⎟

⎠

⎞

⎜

⎝

⎛

+⋅+ zzx

;2

7

12

7

3

=−++ zzx

.

7

5

7

11

zx −=

Получили:

⎪

⎩

⎪

⎨

⎧

−

+=

−=

число. любое

;

7

4

7

1

;

7

5

7

11

z

zy

zx

Получили множество решений. Например,

⎭

⎬

⎫

⎩

⎨

⎧

===

7

1

,

7

11

,0 yxz

или

⎭

⎬

⎫

⎩

⎨

⎧

===

7

5

,

7

6

,1 yxz и другие, которые получаются при различных

z.

Проверку сделаем для любого из наборов, например, для первого:

⎪

⎩

⎪

⎨

⎧

−

==++

==+−

==++

.5

7

35

0

7

2

7

33

;3

7

21

0

7

1

7

22

;2

7

14

0

7

3

7

11

верно.

Ответ:

⎪

⎩

⎪

⎨

⎧

+=

−=

;

7

4

7

1

;

7

5

7

11

zy

zx

−

z любое число. Решений множество.

Пример 3.

⎪

⎩

⎪

⎨

⎧

=++

=++⋅

=

+

−

.3

;53

;1

zyx

(

)( )

.

1

2

1

100

240

111

~

2

1

2

1

020

240

111

~

13

3

5

1

111

113

111

⎟

⎠

⎞

⎜

⎝

⎛

−−

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

−−−

⎟

⎠

⎞

⎜

⎝

⎛

−

=A

Получили:

⇒

⎪

⎩

⎪

⎨

⎧

=

=⋅−⋅−

=+−

;1

;224

;1

z

zy

zyx

.1

;2124

;1

=

=⋅−⋅−

=

y

z

;11111 =−+

=

−

+

=

zy

x

Проверка:

Карасева Р.Б.Высшая математика.Ч1.Электронное учебное пособие

Подождите немного. Документ загружается.