Keyfitz N., Caswell H. Applied Mathematical Demography

Подождите немного. Документ загружается.

13.1. Eigenvalue Sensitivity 315

The numerator of (13.1.37) depends on whether P is constant or depends

on α. We consider these two cases separately.

Case 1: Constant P

In this case,

∂F

∂α

= −a(λ)c(λ)Pλ

−α

log(λ)

= −log λ

1 − Φ(λ)

. (13.1.38)

We calculate ∂F/∂λ by rewriting the characteristic equation as

1=F(λ)=

∞



i=1

−i

(13.1.39)

from which

∂F

∂λ

= −λ

−1

∞



i=1

−i

= −λ

−1

A, (13.1.40)

where

A is the mean age of the parents in the stable population (see Section

11.3.5). Thus, from (13.1.37)

∂λ

∂α

−λ log(λ)

1 − Φ(λ)

. (13.1.41)

From this, it follows immediately that ∂λ/∂α < 0 whenever λ>1; slow-

ing development anywhere in the life cycle of an increasing population

reduces λ. The sensitivity of λ to changes in development rate is inversely

proportional to generation time.

Case 2: P = e

−µα

The probability of surviving from one stage to another is unlikely to be

independent of the time required for the transition. If the survival proba-

bility P represents the results of exposure for α time units to a mortality

rate µ,thenP =exp(−µα), and the numerator of (13.1.37) becomes

−

∂F

∂α

=(logλ + µ)

1 − Φ(λ)

. (13.1.42)

The denominator, ∂f/∂λ is still given by (13.1.40). Thus

∂λ

∂α

−λ(log λ + µ)

1 − Φ(λ)

. (13.1.43)

Comparing this with (13.1.41), it is apparent that making survival prob-

ability dependent on development rate makes it even more diﬃcult for an

increase in α to increase λ.

316 13. Perturbation Analysis of Matrix Models

13.1.7 Predictions from Sensitivities

The sensitivities can be used to predict the response of λ to changes, of

any size, in any or all of the parameters. Let ∆a

be the perturbation (not

necessarily small) of a

and ∆λ the resulting change in λ. From (13.1.24)

we know that the total diﬀerential of λ is

dλ =



i,j

∂λ

∂a

∆a

(13.1.44)

and

∆λ ≈ dλ (13.1.45)

with an error that goes to zero faster than ∆a

. Hence the growth rate

after the perturbation, λ



= λ +∆λ is



≈ λ +



i,j

∂λ

∂a

∆a

. (13.1.46)

The approximation (13.1.46) can be made as accurate as desired by making

the ∆a

small enough. It would be exact, regardless of the size of ∆a

if λ were a linear function of the a

. It is not, but experience suggests

that the nonlinearity in λ is not usually severe (e.g., Caswell 2000a, de

Kroon et al. 2000, Levin et al. 1996). So the sensitivities can be used to

explore scenarios involving even relatively large changes in the vital rates.

Of course, if the perturbations are too large, or you need extreme accuracy,

any perturbation scenario can always be simulated.

13.1.8 Another Interpretation of Reproductive Value

Our ﬁrst interpretation of the left eigenvector v as a measure of repro-

ductive value was in terms of the eﬀects of initial population structure on

asymptotic population size (Chapter 9). The sensitivity formula (13.1.8)

provides another justiﬁcation for equating reproductive value with v. Con-

sider a stage j that can contribute individuals to two other stages, 1 and

2. Increases in either a

or a

will increase λ, and a reasonable measure

of the “value” of stages 1 and 2 is the relative sensitivity of λ to changes

in a

and a

∂λ/∂a

. (13.1.47)

That is, the relative sensitivity of λ to changes in a

and a

is given by

the relative magnitudes of v

and v

. An individual in stage j, confronted

with the choice of contributing to stage 1 or stage 2 and desiring to increase

13.2. Elasticity Analysis 317

λ, should contribute to the stage with the higher value of v

—that is, to

the more valuable stage.

13.2 Elasticity Analysis

It is often useful to compare perturbations on a proportional scale (what

is the eﬀect of a 10 percent decrease in fertility compared to a 10 percent

decrease in survival?).

The proportional response to a proportional per-

turbation is known as elasticity in economics (e.g., Hicks 1939, p. 205).

Caswell et al. (1984) and de Kroon et al. (1986) introduced the calculation

of the elasticity of the eigenvalues to changes in the vital rates.

The elasticity of λ with respect to a

is deﬁned as

∂λ

∂a

(13.2.1)

∂ log λ

∂ log a

. (13.2.2)

That is, the elasticity e

is just the slope of log λ plotted against log a

Since equal increments on a log scale correspond to equal proportions on

an arithmetic scale, the elasticity measures proportional sensitivity. Elas-

ticities can be calculated only for inherently nonnegative quantities like

λ.

The elasticities can be conveniently calculated and displayed as an elasticity

matrix

E =



∂λ

∂a



(13.2.3)

S ◦ A, (13.2.4)

where S is the sensitivity matrix (13.1.10) and ◦ denotes the Hadamard

(element-by-element) product.

13.2.1 Elasticity and Age

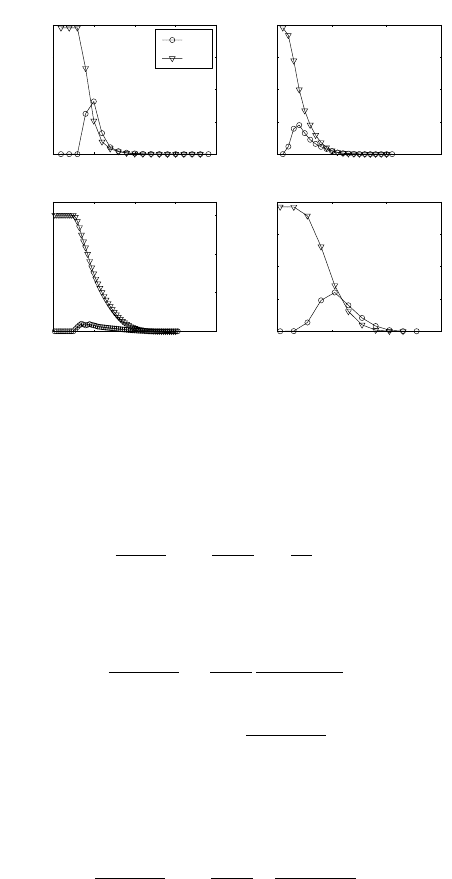
Figure 13.5 shows the elasticity of λ to survival and fertility for four age-

classiﬁed populations. They are quite diﬀerent from the sensitivity patterns

(cf. Figure 13.1). The elasticity of λ to survival probability consistently

declines with age, but the elasticity of λ to fertility ﬁrst increases and then

This is of particular concern to biologists who work with organisms in which transi-

tion probabilities (which may not exceed 1) and fertilities (which may be much greater

than 1) are measured on diﬀerent scales.

318 13. Perturbation Analysis of Matrix Models

0 5 10 15 20

0.05

0.1

0.15

0.2

Elasticity of λ

C. oryzae

0 10 20 30

0.05

0.1

0.15

0.2

M. orcadensis

0 20 40 60 80

0.015

0.03

0.045

Age

O. orca

Elasticity of λ

0 20 40 60

0.05

0.1

0.15

0.2

Age

H. sapiens

Figure 13.5. Elasticities of λ to changes in age-speciﬁc survival (P

) and fertility

) for the four populations whose sensitivities are shown in Figure 13.1.

declines. These are general properties of age-classiﬁed models (cf. Section

13.1.2). The elasticity to fertility at successive ages satisﬁes

1,j+1



j+1





, (13.2.5)

which need not be greater than 1. The elasticity to survival at successive

ages satisﬁes

j+1,j

j+2,j+1

j+1

∂λ/∂P

j+1

(13.2.6)

= λ +

j+1

j+2

(13.2.7)

[cf. (13.1.19)]. This ratio is always greater than 1 when λ ≥ 1.

Equation (13.2.7) implies that the elasticity of λ to survival is the same

for all pre-reproductive age classes.

j+1,j

j+2,j+1



j+1



j+1

j+2

j+1

(13.2.8)

and if F

= F

j+1

=0,thenv

j+1

= P

j+1

−1

j+2

and this ratio is equal

to 1. See Heppell et al. (2000) for an application of this result to models

based on limited demographic data.

13.2. Elasticity Analysis 319

Dormant

seeds

Rosettes

Flowering

Dormant

seeds

Figure 13.6. The contributions to λ, expressed as percentages, of the pathways in

the teasel life cycle (Figure 11.2). Only contributions of more than 1 percent are

shown. Heavy arrows indicate those pathways contributing 5 percent or more of

λ.

13.2.2 Elasticities as Contributions to λ

The elasticities of λ with respect to the a

are often interpreted as the

“contributions” of each of the a

to λ. This interpretation relies on the

fact that the elasticities of λ with respect to the a

sum to 1 (De Kroon

et al. 1986), a result which follows from Euler’s theorem on homogeneous

functions (Mesterton-Gibbons 1993).



An eigenvalue is a homogeneous function of degree one of the a

, because

if Aw = λw,thencAw = cλw; i.e., multiplying all the a

by c is equivalent

to multiplying λ by c.Sinceλ is homogeneous of degree 1,



∂λ

∂a

=1. (13.2.11)

Thus, e

can be interpreted as the proportional contribution of a

to λ.

This decomposition of λ is the only expression of the form

λ =



i,j



A function f (x

,...,x

) is homogeneous of degree k if, for any real constant c,

f (cx

,...,cx

)=c

f (x

,...,x

). (13.2.9)

Euler’s theorem states that if f (x

,...,x

) is homogeneous of degree k,then

∂f

∂x

+ ···+ x

∂f

∂x

= kf(x

,...,x

) (13.2.10)

(e.g., Gillespie 1951).

320 13. Perturbation Analysis of Matrix Models

where the contributions b

can be written as the product of one term that

is a function only of i and another that is a function only of j (Caswell

1986).

The idea of a “contribution” must be interpreted carefully, since λ is

not actually composed of independent contributions from each of the a

Consider the model for the human population of the United States, in which

the elasticity of λ to P

is 0.19 (Figure 13.5). We would say that survival

of age-class 2 contributes about 20 percent of λ. But if we eliminate this

transition, by setting P

= 0, we eliminate not 20 percent but 100 percent

of λ.WhenP

= 0, no one survives to reproduce and λ =0.Thusthe

“contributions” of the other vital rates to λ depend on the value of P

,and

vice versa.

Example 13.4 Elasticity in the desert tortoise

Figure 13.2 shows the elasticities of λ to changes in F

, P

,andG

for the desert tortoise (Doak et al. 1994). The total of the fertility

elasticities is only 0.043 (i.e., 4.3 percent). The elasticities to growth

) sum to 25.8 percent and those to stasis (P

) sum to 69.9 percent.

The largest elasticity is e

; i.e., the elasticity of λ to the probability

) of surviving and staying in size class 7.

Example 13.5 Elasticity in the teasel life cycle

Figure 13.6 shows the largest elasticities in the teasel life cycle (cf.

Figure 11.2). If the elasticities are interpreted as contributions, only

ﬁve arcs, shown by heavy arrows, contribute more than 5 percent to λ.

To a good approximation (73 percent of λ), the growth rate of teasel

can be described in terms of only three transitions: [ﬂowering plants

→ medium rosettes → large rosettes → ﬂowering plants]. Adding the

pathway [ﬂowering plants → dormant seeds → large rosettes] adds

an additional 13 percent of λ.

13.2.3 Elasticities of λ to Lower-Level Parameters

The elasticity of λ to a lower-level variable x is

∂λ

∂x



i,j

∂λ

∂a

∂x

. (13.2.12)

This gives the proportional change in λ resulting from a proportional

change in x, but since there is no reason to expect that λ is a homoge-

neous function of x, the lower-level elasticities do not in general sum to 1,

nor can they be interpreted as contributions to λ.

13.3. Sensitivities of Eigenvectors 321

Example 13.6 Survival and growth in the desert tortoise

The elasticities of λ to changes in survival and growth in the desert

tortoise can be obtained directly from (13.1.31) and (13.1.34):

∂λ

∂σ

(1 − γ

)

∂λ

∂P

∂λ

∂G

(13.2.13)

∂λ

∂P

∂λ

∂G

(13.2.14)

(i.e., the elasticity of λ to σ

is the sum of the elasticities to P

and

), and

∂λ

∂γ



∂λ

∂G

−

∂λ

∂P



. (13.2.15)

These results are shown in Figure 13.2.

13.3 Sensitivities of Eigenvectors

Perturbations of A change the eigenvectors as well as the eigenvalues. We

have already seen some results on the sensitivity of the stable age distri-

bution to changes in parameters (Sections 5.7 and 10.1). Here we derive

some general sensitivity results (Caswell 1980, following the approach of

Faddeev and Faddeeva 1963 and Desoer 1967).

Denote the eigenvalues, right eigenvectors, and left eigenvectors of A

by λ

, w

,andv

, respectively. We assume that the eigenvalues are dis-

tinct, and that the eigenvectors have been scaled so that w

, v

 = 1 and

w

, v

 =0fori = j.

Suppose that we are interested in w

and v

. As in the derivation of the

eigenvalue sensitivities, we begin with

= λ

. (13.3.1)

Taking the diﬀerential of both sides yields

(dA)w

+ A(dw

)=(dλ

+ λ

(dw

). (13.3.2)

If we consider dλ

as known, (13.3.2) is a linear equation in the diﬀerential

(A − λ

I)dw

=(dλ

I − dA)w

. (13.3.3)

Since (A − λ

I) is singular, (13.3.3) cannot be solved directly for dw

However, we can write any solution as a linear combination of the

eigenvectors:



m=1

(13.3.4)

322 13. Perturbation Analysis of Matrix Models

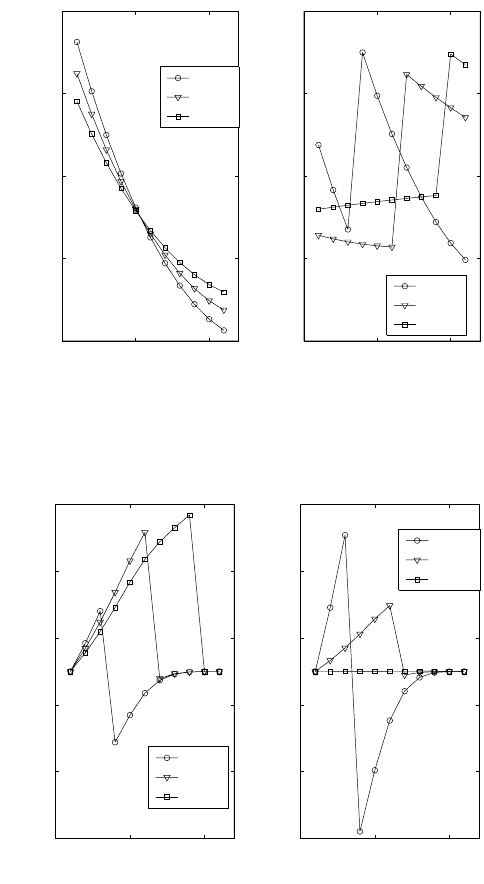
0 5 10

−0.06

−0.02

0.02

0.06

0.1

Age class

Sensitivity of w

to F

0 5 10

−0.08

−0.04

0.04

0.08

Age class

to P

Figure 13.7. The sensitivity of the scaled stable age distribution w to changes in

fertility (F

, F

, and F

) and survival (P

, P

, and P

) for the population of the

United States. The vector w is scaled so that



=1.

0 5 10

−1

−0.6

−0.2

0.2

0.6

e class

Sensitivity of v

to F

0 5 10

−0.5

−0.3

−0.1

0.1

0.3

0.5

e class

to P

Figure 13.8. The sensitivity of the scaled reproductive value vector v to changes

in fertility (F

, F

, and F

) and survival (P

, P

, and P

) for the population of

the United States. The vector v is scaled so that v

=1.

13.3. Sensitivities of Eigenvectors 323

for some as yet unknown coeﬃcients k

.Thevalueofk

is irrelevant, since

when (13.3.4) is substituted in (13.3.3), k

(A − λ

I)w

= 0, regardless of

the value of k

. In what follows, we will set k

= 0; this turns out to be the

only reasonable assumption.

Leaving this expression for dw

aside for the moment, form the scalar

product of both sides of (13.3.2) with v

,forj =1:

(dA)w

, v

 + Adw

, v

 = dλ

w

, v

 + λ

dw

, v

. (13.3.5)

The second term on the left-hand side of (13.3.5) simpliﬁes to λ

dw

, v

,

and the ﬁrst term on the right-hand side is zero if j = 1. Simplifying yields

dw

, v

 =

(dA)w

, v



− λ

. (13.3.6)

Now, substitute (13.3.4) for dw

into (13.3.6) to obtain



m=1

w

, v

 =

(dA)w

, v



− λ

. (13.3.7)

Since w

, v

 =0forj = m, and equals 1 for j = m, (13.3.7) simpliﬁes

to an expression for k

(dA)w

, v



− λ

. (13.3.8)

When (13.3.8) is substituted into (13.3.4), we obtain the desired expression

for the diﬀerential of the right eigenvector w



m=1

(dA)w

, v



− λ

. (13.3.9)

The corresponding expression for the diﬀerential of the left eigenvector v

follows from noting that the left eigenvectors of A are the right eigenvectors

of A

∗

,sothat



m=1

(dA

∗

, w



−

. (13.3.10)

The partial derivatives of w

and v

follow from supposing that only

asingleentry,saya

, is perturbed. Using superscripts to distinguish the

eigenvectors and subscripts to denote their elements (e.g., w

(m)

is the jth

element of w

), the resulting expressions are

∂w

∂a



m=1

(1)

¯v

(m)

− λ

= w

(1)



m=1

¯v

(m)

− λ

(13.3.11)

324 13. Perturbation Analysis of Matrix Models

∂v

∂a

= v

(1)



m=1

¯w

(m)

−

. (13.3.12)

13.3.1 Sensitivities of Scaled Eigenvectors

The stable stage distribution is often scaled so that



= 1 (to represent

proportions) or



= 100 (to represent percentages). The reproductive

value vector is usually scaled so that v

= 1, to measure reproductive

value relative to a newborn individual. The sensitivities of these scaled

eigenvectors can be calculated using (13.3.11) and (13.3.12).

Let ||w|| =



| and suppose the scaled stable stage distribution is

given by w/||w||. Its sensitivity is then given by

∂

∂a

w

∂w

∂a

||w|| − w



∂w

∂a

||w||

. (13.3.13)

If the eigenvector whose sensitivity is being evaluated is already scaled so

that ||w|| = 1, this simpliﬁes to

∂

∂a

w

∂w

∂a

− w



∂w

∂a

, (13.3.14)

where ∂w/∂a

is given by (13.3.11).

Similarly, if the scaled reproductive value vector is deﬁned as v/v

,and

if the vector whose sensitivity is being evaluated is already scaled so that

= 1, the sensitivity of the scaled reproductive value vector is

∂

∂a

∂v

∂a

− v

∂v

∂a

. (13.3.15)

Example 13.7 An age-classiﬁed population

The sensitivities of w and v for the U.S. population are shown in

Figures 13.7 and 13.8. Increasing fertility shifts the age distribution

to younger ages, because it increases λ (fertilities aﬀect the stable age

distribution only through λ). Changes in fertility at young ages have

a greater eﬀect on λ, and hence on w, than do changes at later ages.

An increase in survival at age i increases the representation of age

class i + 1 in the stable age distribution. Since the age distribution is

constrained to sum to 1, this produces a decrease in the representation

of some other classes.

Figure 13.8 shows the sensitivity of reproductive value to changes

in fertility. Increasing F

increases the v

at all age classes up to

and including i, and reduces v

at later ages (because the values

are all scaled relative to v

). Changes in survival probability have

qualitatively similar patterns. Thus, increasing survival probability