Klein B. FEM: Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen

Подождите немного. Документ загружается.

14 Grundregeln der FEM-Anwendung

318

Der Grundalgorithmus einer einfachen Koeffizientenvertauschung, welches äquivalent einer

Knotennummerierung ist, geht auf Rosen zurück. Obwohl das Verfahren einsichtig und ein-

fach ist, bereitet es Probleme bei sehr großen Matrizen und bei einer ungünstigen Ausgangs-

nummerierung. Hiergegen benutzt der Cuthill-McKee-Algorithmus einen vier- oder fünfsei-

tigen Graphen, der über das zu nummerierende Gebiet aufgespannt wird und vertauscht darin

die Knotennummern solange, bis innerhalb eines Graphen die Differenz der Knotennum-

mern minimal ist. Bei dieser Abstimmung werden auch die angrenzenden Graphen mit be-

rücksichtigt. Die ansonsten noch angegebenen Verfahren stellen im Kern nur Abwandlungen

des CMK-Algorithmus dar und sollen daher ohne nähere Erläuterung angegeben werden.

Um nun die Wirksamkeit einer Bandbreitenreduzierung ausweisen zu können, ist im vor-

stehenden Bild ein Gebiet mit einer bewusst ungünstigen Nummerierung erzeugt worden.

Man erkennt an der Auswertung, dass alle Verfahren die Bandbreite der Steifigkeitsmatrix

deutlich reduzieren.

Im Grunde genommen ist jedoch die Bandbreite nicht das alleinige Kriterium für einen ge-

ringen Speicherbedarf und geringe Rechenzeit, sondern hierbei ist auch das numerische

Rechenverfahren für die Gleichungslösung mitentscheidend. Wird insbesondere das Glei-

chungslösungsverfahren von Cholesky benutzt, so ist das

Profil der Steifigkeitsmatrix gleich

wichtig. Mit Profil wird dabei die effektiv benötigte Anzahl von Koeffizienten bezeichnet,

die für die Gleichungslösung unbedingt erforderlich sind. Bandbreite und Profil hängen na-

türlich unmittelbar zusammen, sodass durch eine Umnummerierung beides beeinflusst wird.

14.5 Genauigkeit der Ergebnisse

Zum Einstieg in das Manuskript wurde ausgeführt, dass die Methode der finiten Elemente

heute als das leistungsfähigste numerische Verfahren des Ingenieurwesens gilt. In der Tat ist

es auch so, dass bei richtiger Modellbildung und abgestimmten Eingangsdaten eine sehr gute

Übereinstimmung der theoretischen Ergebnisse mit überprüfenden Experimenten erzielt

werden konnte. So war es beispielsweise am Fachgebiet für Leichtbau-Konstruktion an der

Universität Kassel möglich, statisch belastete Strukturen mit etwa 7 % Abweichung zu

DMS-Messungen hinsichtlich der Spannungsverteilung zu analysieren oder ein Eigenfre-

quenzspektrum bis auf 5 % Abweichung zu entsprechenden Resonanzprüfungen zu ermit-

teln. Dies bedarf natürlich einer sorgfältigen Arbeitsweise und einer dezidierten

Abstimmung bezüglich

 der Feinheit des Netzes,

 der gewählten Elementtypen,

 des Werkstoffverhaltens und der Werkstoffdaten

sowie

 der numerischen Genauigkeit der Rechnung.

Auf die ersten beiden Aspekte ist zuvor schon eingegangen worden, sodass wir diese Aus-

sage nur noch durch eine Bemerkung bezüglich der Netzfeinheit ergänzen wollen. Hierzu

beziehen wir uns auf die Konvergenzbetrachtungen der vorstehenden Kapitel, aus denen

unter anderem die Erkenntnisse abzuleiten sind, dass man bei Zugrundelegung eines be-

stimmten Netzes nie den Abstand zum exakten Ergebnis weiß. Einige Programmsysteme

14.6 Qualitätssicherung

319

bieten daher die Möglichkeit, quasi auf Knopfdruck ein Netz doppelt so fein zu machen.

Stellt man dann bei einer erneuten Rechnung fest, dass es nur noch geringere Änderungen

zur vorausgegangenen Rechnung gibt, so kann man das erste Ergebnis quasi als ausreichen-

de Näherung ansehen. Dass ein derartiges Vorgehen praktizierbar ist, belegt unter anderem

die Tatsache, dass sich die Rechenleistung der Supermikro-Rechner in den letzten 3 Jahren

mehr als verzehnfacht hat. Einen weiteren Ansatzpunkt für ein gutes Ergebnis ergibt sich

auch in der programmtechnischen Möglichkeit, ein Gleichungssystem doppelt genau zu lösen.

Die Programmsysteme, die diese Verhaltensweise zeigen, bezeichnet man als so genannte

Versionen, womit zum Ausdruck gebracht wird, dass die Ergebnisgüte eine Funktion des

relevanten Elementdurchmessers h ist. Gänzlich anderes Verhalten zeigen hingegen Pro-

gramme der so genannten

p-Versionen (z. B. PROBE /N.N. 94/), die den Polynomgrad p der

Ansatzfunktion als variabel ansetzen. Bei einer gleich feinen Elementteilung können also mit

einer p-Version mehr Freiheitsgrade in einem Gebiet untergebracht werden und somit ein

aussagefähigeres Ergebnis erzielt werden.

Zum Konvergenzverhalten sei noch angemerkt, dass unter Benutzung beschränkter verträgli-

cher Verschiebungszustände die gefundene Lösung für eine Struktur eine wertvolle Grenzei-

genschaft besitzt, die in der Überschätzung der Formänderungsenergie besteht:

 Für eine gegebene Belastung wird deshalb die berechnete Formänderungsenergie kleiner

oder höchstens gleich sein der Formänderungsenergie in der realen Struktur. Dies lässt

sich damit erklären, dass die reale Struktur keine Beschränkung hinsichtlich der mög-

lichen Verschiebungen kennt.

Die mit der Verschiebungsmethode gefundene Lösung muss somit immer eine untere

Schranke für die Verschiebungen darstellen.

 Bei vorgeschriebenen Verschiebungen wird die berechnete Formänderungsenergie dage-

gen eine obere Schranke darstellen, sodass dann die Kräfte immer zu groß bestimmt wer-

den.

Diese unter anderen von Rayleigh für linear elastische Strukturen formulierte Aussage gilt

im Wesentlichen auch für nichtlineares Materialverhalten und Temperaturbelastung.

Neben den methodischen und numerischen Verbesserungsmöglichkeiten spielen auch noch

die Werkstoffdaten eine nicht zu unterschätzende Rolle, da hiermit die Steifigkeit eines Bau-

teils bestimmt wird. So haben wir vorstehend erkannt, dass bei linear elastischen Rech-

nungen die Querkontraktionszahl

Q und der Elastizitätsmodul E bzw. bei nichtlinearen Rech-

nungen zusätzlich noch die Fließgrenze R

und bei dynamischen Rechnungen ergänzend

noch die Dichte

U mit zu den Eingangsgrößen gehören. Bei Verwendung von Standard-

werten für diese Größen muss man sich natürlich auch über die statistischen Größen und die

damit erzielten Rechnerergebnisse im Klaren sein, die dann nur für eine Werkstoffgruppe

gelten.

Strebt man hingegen eine Aussage an, die letztlich auch mit einem Experiment in Einklang

steht, so ist es notwendig, abgesicherte Materialdaten zu verwenden. Dies soll unter anderem

auch das Bild 14.11

verdeutlichen, das beispielsweise Materialkenngrößen verschiedener

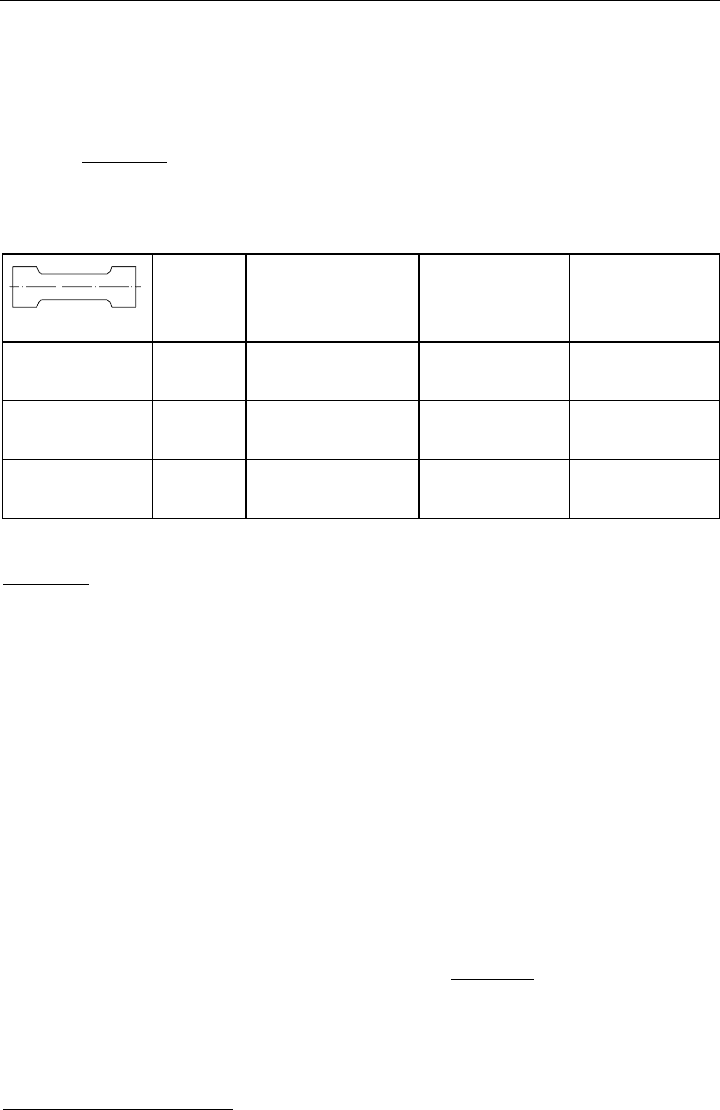
14 Grundregeln der FEM-Anwendung

320

Stähle

aufführt, die im Labor des Fachgebiets Leichtbau-Konstruktion an der Universität

Kassel gemessen wurden.

Strebt man hingegen eine Aussage an, die letztlich auch mit einem Experiment in Einklang

steht, so ist es notwendig, abgesicherte Materialdaten zu verwenden. Dies soll unter anderem

auch das Bild 14.11 verdeutlichen, das beispielsweise Materialkenngrößen verschiedener

Stähle aufführt, die im Labor des Fachgebiets Leichtbau-Konstruktion an der Universität

Kassel gemessen wurden.

Werkstoffe

RbzwR

eH p

,02

N/mm

C 22 0,277

328

(min. 240)

499

(min. 430)

205.600

(210.000)

C 45 0,28

496

(min. 340)

708

(min. 620)

197.300

(210.000)

QStE 500 0,315

625

(min. 500)

777

(min. 550-700)

196.300

(210.000)

Bild 14.11: Materialkennwerte einiger Stähle (Vergütungs- und Feinkornstahl) im Vergleich

Es fällt hierbei auf, dass die Abweichungen von den bekannten Standardwerten für Stahl



N/mm101,2E;3,0Ȟ  teils noch erheblich sind. Damit wird offensichtlich, dass

die Materialdaten manchmal eine nicht zu vernachlässigende Fehlergröße darstellen.

Resümierend lässt sich feststellen, dass FEM-Ergebnisabweichungen auf systematische Feh-

ler (numerische Fehler, Approximationsfehler) und stochastische Abweichungen (Abmes-

sungsschwankungen, streuende Materialdaten) zurückzuführen sind.

14.6 Qualitätssicherung

Mit der Etablierung der FEM als Standardwerkzeug der Produktentwicklung unterliegt auch

eine interne oder externe Dienstleistung zunehmend den Maßstäben von Qualitätssiche-

rungsmodellen. Bestreben ist es, die Ausführungsqualität von Berechnungen zu erhöhen, in

dem diese nachvollziehbar und überprüfbar gemacht sowie persönliche Verantwortlichkeiten

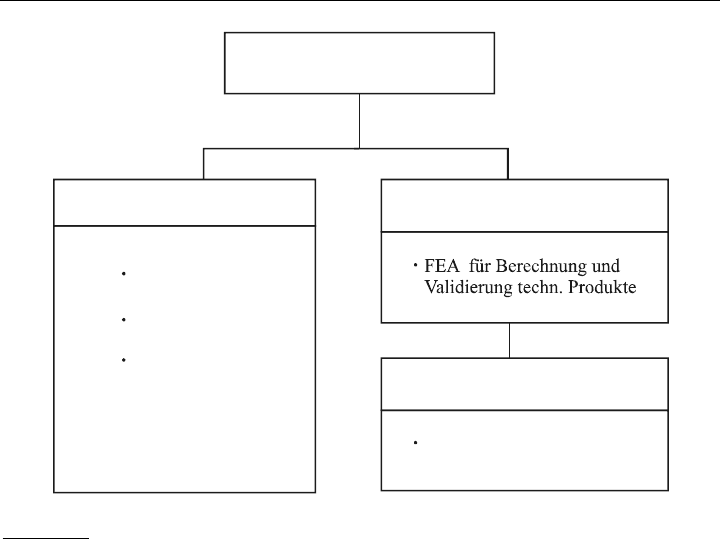
geschaffen werden. In der Industrie wurden dazu die im Bild 14.12 herausgestellten Darle-

gungsmodelle festgeschrieben.

Anmerkung: Qualitäten nach DIN EN 10 083-1 und DIN EN 10 113

14.6 Qualitätssicherung

321

DIN EN ISO 9001:2000

Produkte

Dienstleistungen

Prozesse

NAFEMS QSS

Qualitätsmodelle

SAFESA

strukturierte Vorgehensweise

für FEA

Bild 14.12:

Industrielle Qualitätssicherungsmodelle

Am verbreitetsten ist die DIN EN ISO 9000:2000, welche ein QM-Prozessmodell für ent-

wickelnde und produzierende Unternehmen sowie Dienstleister darlegt. Dies ist ein Organi-

sationsrahmen, der auf die fehlerfreie Erbringung aller Arbeitsschritte ausgerichtet ist. Durch

eine Zertifizierung müssen die Unternehmen nachweisen, dass sie dieses Qualitätsmodell

(Prozessorganisation, QM-Handbuch) aufrechterhalten und tatsächlich leben.

Parallel dazu wurde mit NAFEMS QSS (Quality System Supplement to ISO 9001) ein Stan-

dard mit alleiniger Ausrichtung auf FEM-Dienstleistungen geschaffen. Die Erweiterung um-

fasst insbesondere Forderungen an die Personalqualifikation, Software und die Risikokate-

gorie des Produktes. Hiernach muss ein FEM-Berechner über ausreichende Berufserfahrun-

gen verfügen, Produktverständnis und Fachkenntnisse in der FE-Methode sowie der

Numerik der Algorithmen aufweisen. Weiterhin muss ein Berechnungsprojekt strukturiert

geplant werden und über die Stufen Modellierung, Berechnung und Ergebnisinterpretation

nachvollziehbar sein. Der ergänzende SAFESA-Standard gipfelt in der Forderung: Keine

Freigabe von FE-Ergebnissen ohne Prüfung.“ und „100-%-Prüfung bei sicherheitsrelevanten

Bauteilen. Bei „nicht sicherheitsrelevanten Bauteilen“ ist zumindest „die Richtigkeit eines

Ergebnisses stichprobenhaft“ abzusichern. Damit sind die

künstlerischen Freiheiten von FE-

Berechnern zurückgeschnitten und die Projektverantwortung in den Mittelpunkt gerückt

worden.

Eine noch andere Dimension gibt in diesem Zusammenhang das Produkthaftungsgesetz

(ProdHaftG) vor, welches den rechtlichen Rahmen für den Berechnungsingenieur schafft.

Falls das Versagen eines Bauteils nachweislich auf mangelnde Sorgfalt bei der Berechnung

zurückzuführen ist, greift letztlich das gesamte Strafregister vom BGB bis zum StGB.

322

Fallstudien

Anmerkung: Die nachfolgenden Fallstudien wurden überwiegend mit dem FE-Programm I-DEAS der Firma

EDS bzw. einige ergänzende Rechnungen mit dem System ABAQUS von HKS bearbeitet.

323

Fallstudie 1: zu Kapitel 4 Matrix-Steifigkeitsmethode

In der Literaturstelle von Hahn /HAH 75/ ist dargestellt, dass mit einfachen Stab-Elementen

sehr schön statisch bestimmte und statisch überbestimmte Fachwerkstrukturen behandelt

werden können. Um dies exemplarisch zu untermauern, soll hier die Lösung des so ge-

nannten Navier‘schen Problems übernommen werden.

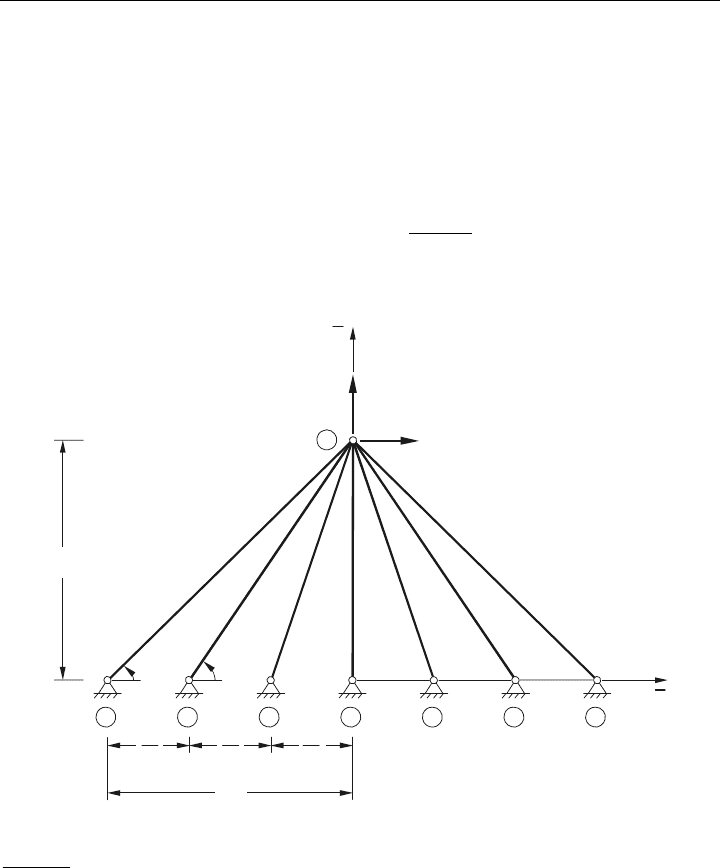
Dieses Problem besteht in der Berechnung der freien Knotenverschiebungen des vielfach

statisch überbestimmten elastischen Fachwerks von Bild 1.1

unter gegebenen äußeren Kräf-

ten. Mit der Lösung haben sich im 17. Jahrhundert viele Mathematiker beschäftigt und sehr

komplizierte Lösungswege entwickelt.

234567

= 0

v= 0

u= 0

v= 0

Bild 1.1: Mehrfach statisch überbestimmte Fachwerkstruktur

Alle Stäbe sollen dabei gleichen Querschnitt (A = konst.) haben und aus gleichem Werkstoff

(E = konst.) bestehen. Wir wählen die Idealisierung so, dass jeder Stab ein finites Element

mit zwei Knoten und jeweils 2 Freiheitsgraden





, sein soll. Bei acht Knoten erhalten

wir so eine 16-x-16-Gesamtsteifigkeitsmatrix.

Da jeder Knoten

c bis i unverrückbar gelagert ist, braucht letztlich aber nur eine 2-x-2-

Matrix



14x1416x16  invertiert werden, welches im Grunde ein leichtes Unter-

fangen darstellt, wie die folgende Lösung zeigt.

Fallstudie 1: zu Kapitel 4 Matrix-Steifigkeitsmethode

324

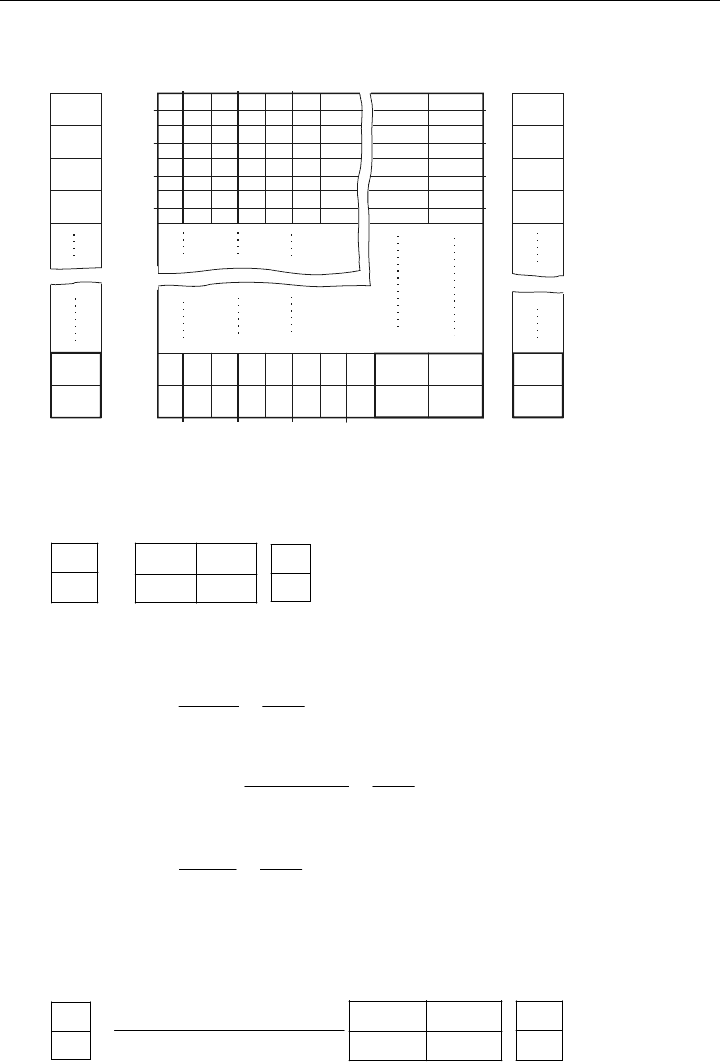
a) Systemgleichung

316

15 15

16 15

15 16

16 16

(1)

b) Kondensierte Lösungsgleichung

16161516

16151515



(2)

mit

1515

sincos

cos

AEk DD



¦¦

, (3)

15161615

sincos

AEkk DD



DD

 {

¦¦

, (4)

¦¦



1616

sin

AEk

. (5)

Für die vorgegebenen Kräfte

y8x8

F,F erhalten wir die unbekannten Knotenverschiebungen

durch Inversion der abgespaltenen Steifigkeitsmatrix zu



15151616

16151616

1615151616161515

kkkk







, (6)

womit dann auch die Verschiebung des Knotenpunktes

j bestimmt ist.

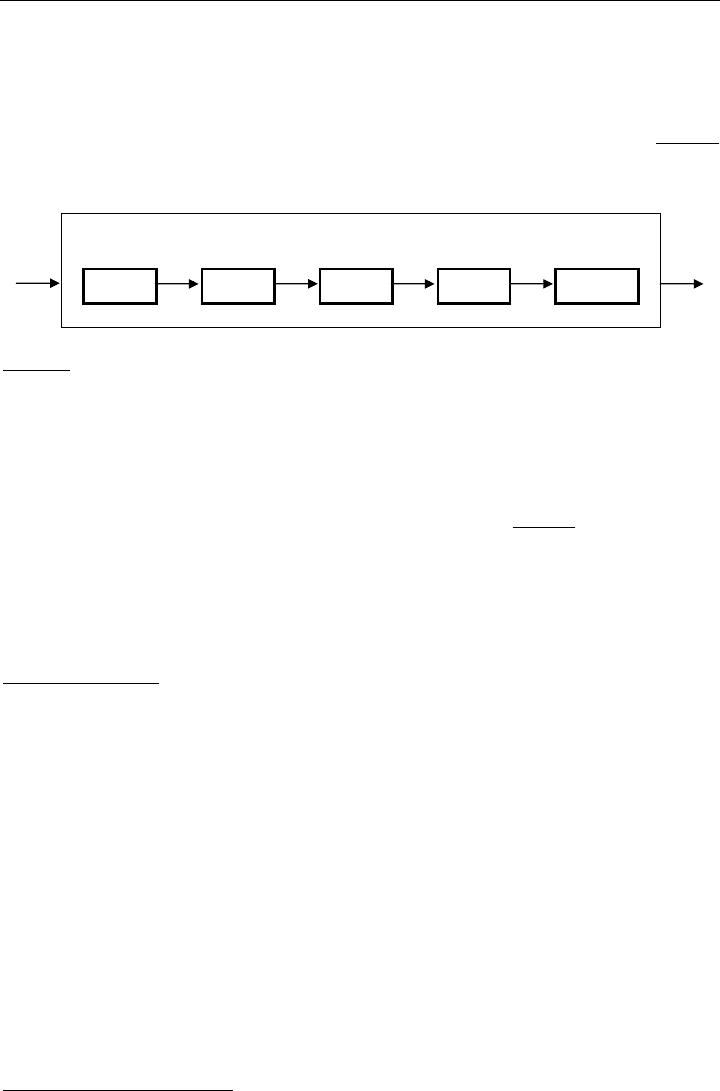
325

Fallstudie 2: zu Kapitel 5 Konzept der FEM / Allgemeine Vorgehensweise

Die Hilfsmittel im Ingenieurwesen entwickeln sich unaufhaltsam zu Computermethoden.

Zukünftige Produktentwickler müssen Fertigkeiten und Kenntnisse in der virtuellen Produkt-

entwicklung aufweisen. Virtuelle Produktentwicklung besteht heute schon, wie im Bild 2.1

dargestellt, aus einer leistungsfähigen Methodenkette.

CAE – Computer Aided Engineering

CAD MKS FEM OPT STL

Bild 2.1: Einsatz rechnerunterstützter Methoden (CAE) vom Konzept zum Produkt

In dieser Fallstudie soll allerdings nur der Weg vom CAD-Modell zum FE-Modell bzw. zur

FE-Berechnung skizziert werden. Das hierfür benutzte Beispiel sei die Druckplatte eines ein-

fachen Papierlochers.

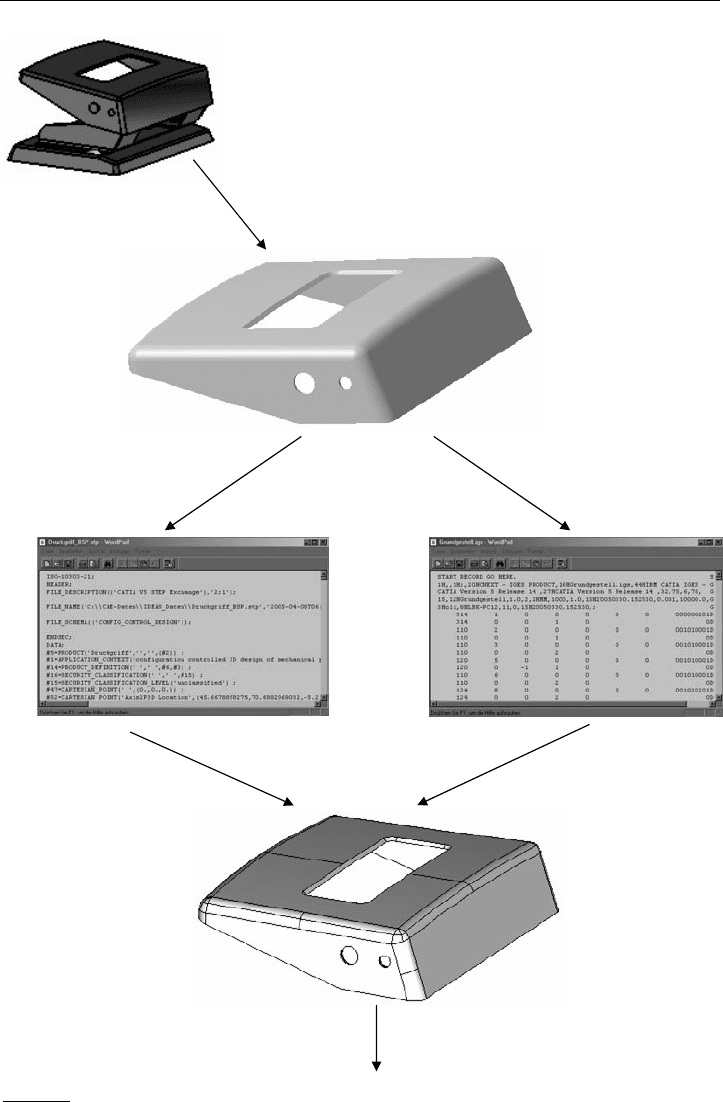
Die erste Stufe vom CAD-Exportfile bis zum FE-Importfile zeigt Bild 2.2. In diesem Fall ist

der ganze Locher mit dem CAD-System CATIA V5 konstruiert worden. Als gefährdetes

Bauteil wird vom Konstrukteur die Handdruckplatte angesehen, die im Weiteren mit einer

FE-Rechnung analysiert werden soll.

Produktentwicklung

1. Das Produkt „Locher“ ist mit CATIA V5 als Volumenmodell entwickelt worden. CATIA

V5 ist ein CAD-System der neuen Generation, welches neben der Zeichnungserstellung

und Bauteilparametrisierung noch über Optionen verfügt, Produktwissen zu verwalten

und bestimmte Anwendungsprozesse (Blechumformung, NC-Bearbeitung, Verkabelung,

Toleranzen, einfache lineare FE-Analysen etc.) zu simulieren.

2. Aus dem CAD-Modell kann natürlich ein Bauteil oder auch eine Baugruppe für eine Wei-

terbearbeitung exportiert werden. Da die Weiterbearbeitung mit einem FEM-System er-

folgen soll, muss ein geeigneter Datentransfer vorgenommen werden. Hierzu stehen soft-

waretechnisch die IGES- und STEP-Schnittelle

zur Verfügung, die Grafik und Techno-

logie austauschen können.

3. In dem FE-Programm bzw. Pre-Prozessor kommt als Importfile ein Volumenmodell an,

welches in unterschiedlicher Weise vernetzt werden kann. Im umseitigen Bild sind die

einzelnen Schritte gemacht worden.

Anmerkung: IGES = Initial Graphics Exchange Spezification

STEP = Standard for the Exchange of Product Model Data (ISO 10303)

Fallstudie 2: zu Kapitel 5 Konzept der FEM / Allgemeine Vorgehensweise

326

Bild 2.2:

Vom CAD-Modell zum Volumenmodell im Pre-Prozessor

3-D-CAD-Modell

Bauteil „Handdruckplatte“

Step-File IGES-File

importiertes Volumen

zur Weiterbearbeitung im FE-

Programm

Fallstudie 2: zu Kapitel 5 Konzept der FEM / Allgemeine Vorgehensweise

327

Bauteilanalyse

4. Das Bauteilmodell liegt nun im Pre-Prozessor eines FE-Programms vor und muss für die

Berechnung weiter aufbereitet werden. Ein wesentlicher Punkt ist hierbei die Auswahl

des Berechnungsmodells.

5. Bei der zu berechnenden Handdruckplatte, die aus einem dünnen Stahlblech gefertigt

wurde, bietet sich ein Schalenmodell geradezu an. Wenn also ein Schalenmodell berech-

net werden soll, muss in dem vorliegenden Bauteil eine „Midsurface“ gebildet und diese

mit der physikalischen Dicke des Teils belegt werden. Gewählt wurden lineare Schalen-

Elemente, die im „free mesh“ vernetzt wurden.

6. In dem anderen Fall ist das importierte Volumenmodell mit parabolischen „Tetraeder-

Elementen“ modelliert bzw. auch durch „free mesh“ vernetzt worden. Dem Tetraeder-

Element liegt ein quadratischer Ansatz zugrunde, der natürlich schneller genauere Ergeb-

nisse ermitteln wird, wie der lineare Schalenansatz.

Der Ablauf vom Bauteilmodell über die Stufen Vernetzung und physikalischer Datensatz (F,

Q, E, ...) ist im umseitigen Bild 2.3 dargestellt. Die unterschiedliche Vorgehensweise hat

natürlich auch Einfluss auf die erzielten Ergebnisse, welches die folgende Tabelle ausweist.

lin. Schalen-Modell quadr. Volumen-Modell

Anzahl „Knoten“ 3.504 18.298

Anzahl „Elemente“ 3.349 8.837

max. Spannung 98 % 100 %

max. Durchbiegung 104 % 100 %

Rechenzeit 1 Sekunde 12 Sekunden

Das qualitativ höherwertige Volumenmodell mit fünfmal mehr Knoten als das Schalen-

modell wird insgesamt näher an der exakten Lösung des Problems liegen. Den Nachteil er-

kennt man in der Rechenzeit, wenn man sich sehr große FE-Modelle vorstellt.

Klein B. FEM: Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen - und Fahrzeugbau

Подождите немного. Документ загружается.