Klein B. FEM: Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen

Подождите немного. Документ загружается.

Fallstudie 7: zu Kapitel 7.5 Anwendung der Volumen-Elemente

338

Diese Elemente werden in modernen FE-Systemen bei automatischen Meshprozeduren, dem

so genannten free meshing, üblicherweise verwendet. Für eine realistische Modellbildung

der Krafteinleitung war es notwendig, ein Stück des Pedalbolzens zu berücksichtigen.

Damit ein möglichst durchschnittliches Fahrerspektrum abgedeckt werden kann, wurde als

maximale Fußkraft N000.1F

gewählt. Das erzeugte Drehmoment wird dann über einen

Vierkant in das Kettenblatt eingeleitet. Da bei der Analyse nur die Augenblicksstellung der

ungünstigsten Krafteinleitung betrachtet wird, kann für die Anbindung an das Vierkantprofil

eine feste Einspannung mit u = 0, v = 0 und w = 0 angenommen werden.

Unter diesen Vorgaben ist im Bild 7.3 zunächst die elastische Verformbarkeit der Kurbel

ausgewertet worden. Es ist erkennbar, dass insbesondere im vorderen Bereich die Knoten

translatorisch und rotatorisch ausgelenkt werden. Die Kurbel muss daher eine ausreichende

Torsions- und Biegesteifigkeit aufweisen.

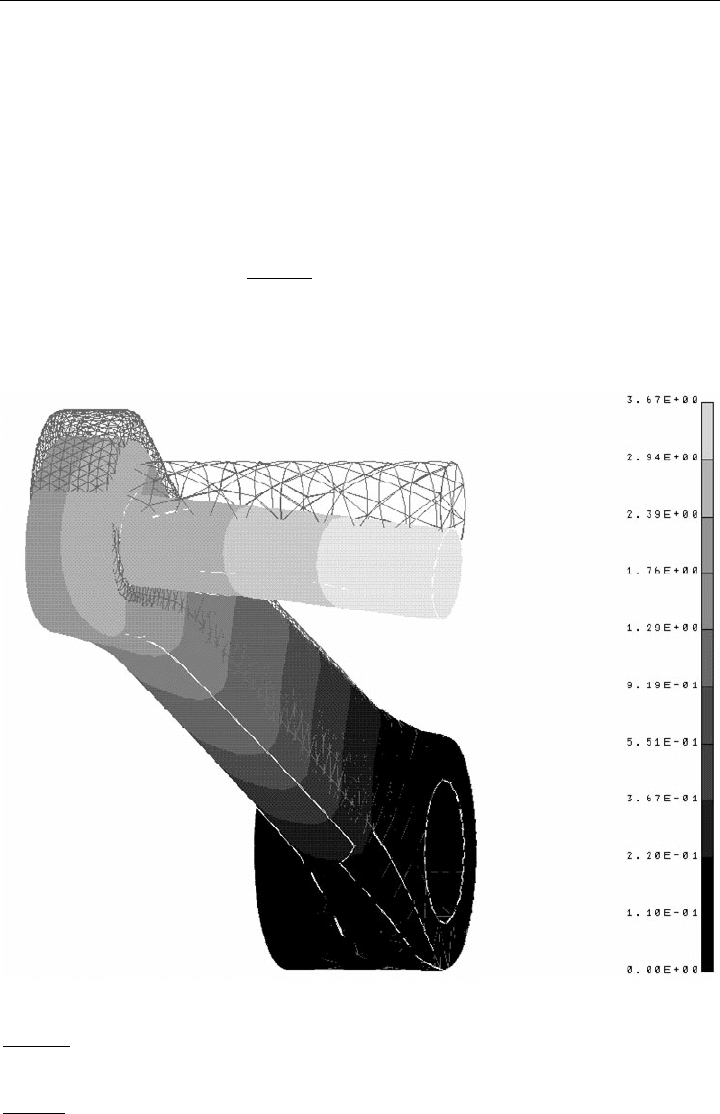
Bild 7.3: Deformation der Tretkurbel bei Belastung

Im weiteren Interesse ist noch abzuklären, ob die Beanspruchung in der Kurbel zulässig ist.

Bild 7.4

zeigt die entsprechende Spannungsauswertung über Isolinien.

Fallstudie 7: zu Kapitel 7.5 Anwendung der Volumen-Elemente

339

Wie zu erwarten war, nehmen die Spannungen zu bzw. verdichten sich an den Randbe-

dingungsstellen. Ausgewertet wurden dabei die Vergleichsspannung



WWWVVVVVVVVV V

xyzxzyyx

3 (1)

nach von Mises.

Bild 7.4:

Spannungsverteilung in der Tretkurbel bei Belastung

Die Spannungen sind aber nicht kritisch, da im Gesenk geschmiedete Al-Legierungen

Streckgrenzenwerte von 200-420

N/mm aufweisen.

340

Fallstudie 8: zu Kapitel 9 Dynamische Probleme

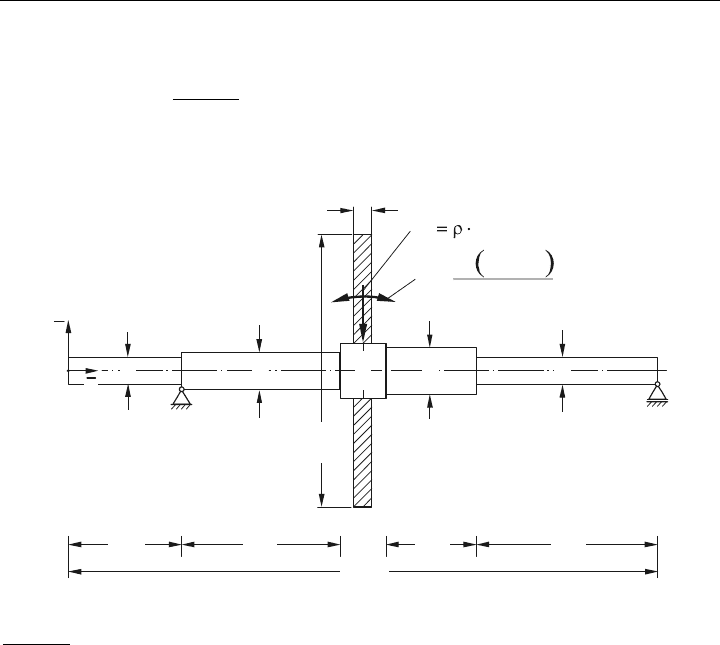
Die nachfolgend im Bild 8.1 dargestellte Welle wird in einer Kartonagenmaschine zum

Schneiden von Pappkartons eingesetzt. Um den Schneidevorgang sauber ausführen zu kön-

nen, sollen die Eigenfrequenzen und Eigenformen dieser Welle berechnet werden.

1300

250 350 200 400100

Ø120

Ø100

Ø60

Ø80

Ø600



mr t3

mg/dk81,7

m/mN101,2E



Bild 8.1: Schneidwelle für Kartonagenmaschine

Wie im Kapitel 9.4 dazu ausgeführt worden ist, gilt es in diesem Fall, das Eigenschwin-

gungsproblem

0UKÜM  (1)

der Biegung zu lösen. Die Dämpfung ist hierbei vernachlässigt worden, da keine sinnvollen

Werte ermittelbar sind.

Für die Idealisierung wählen wir zweckmäßigerweise 2-D-Balken-Elemente. Des Weiteren

bauen wir das Schneidenblatt mit seiner Masse und seinem Massenträgheitsmoment, so wie

im Kapitel 9.2.2 gezeigt, an den entsprechenden Knoten der darunter liegenden Balken-Ele-

mente ein. Das so aufbereitete System ist dann mit dem FEM-Paket I-DEAS mithilfe des

Lanczos-Algorithmus dynamisch durchgerechnet worden.

Bei diesem Berechnungsverfahren müssen, im Gegensatz zu weniger effektiven Lösungsver-

fahren, keine möglichen Vorzugsrichtungen vordefiniert werden. Das Programm untersucht

das ganze FE-Modell selbstständig auf alle vorkommenden Eigenformen. Dadurch ist ge-

währleistet, dass keine Eigenfrequenzen bzw. deren zugehörige Eigenformen vom Bediener

übersehen werden.

Fallstudie 8: zu Kapitel 9 Dynamische Probleme

341

Die Eigenfrequenzen konnten so gefunden werden zu:

66,34



3980,4 1

/min

250,95



s #

15057 1 /min

568,35



s #

34101 1

/min

781



,87 s #

46912,2 1 /min

817,16



49029,6 1 /min

Wir wissen, dass man ein Maschinenelement nie mit seinen Eigenfrequenzen anregen sollte,

da es so zerstört würde. Um also die zulässigen Betriebsbereiche vor Augen zu haben, zeich-

nen wir uns das Frequenzband auf. Hierin ist sofort zu erkennen, welche Betriebszustände

möglich sind, welche Eigenfrequenzen dazu durchfahren werden müssen und wie der Ab-

stand zu den nächstliegenden Anregungen ist. Bei den meisten Anwendungen wird die hier

betrachtete Welle auf Grund der Höhe der Frequenzen nur in der ersten Eigenfrequenz auf

kritische Anregung untersucht werden müssen.









(s )

n (min )

-1

5.000 10.000 15.000 20.000 25.000 30.000 35.000 40.000 45.000 50.000

Bild 8.2:

Frequenzband der Schneidwelle

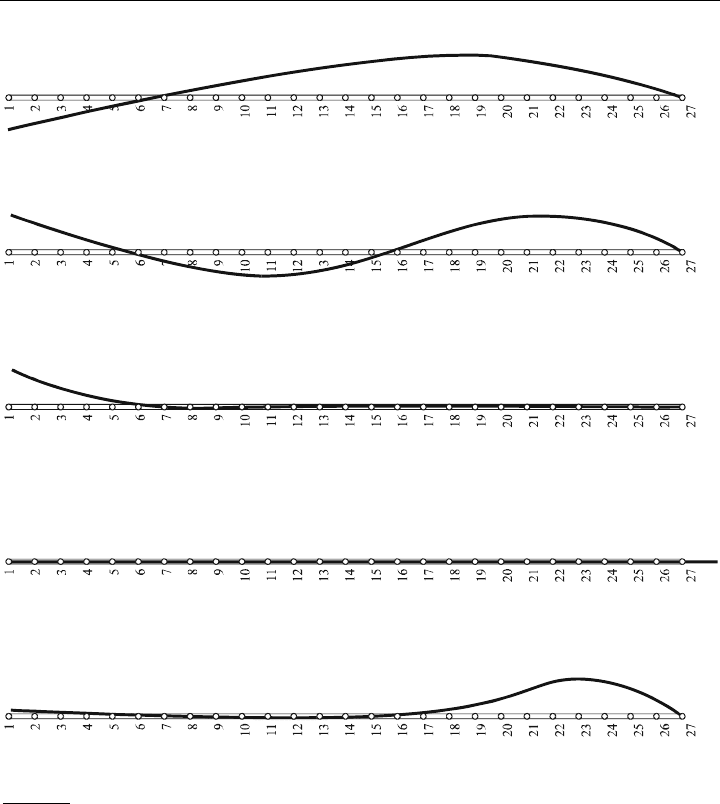
Die sich dabei einstellenden Eigenfrequenzen zeigt das nächste Bild 8.3

. Das Messerblatt

zum Kartonschneiden befindet sich dabei auf der Knotenposition Nr. 14. Aus den Eigen-

formen lässt sich dann mit Bezug auf die dazugehörenden Frequenzen eine Aussage über die

Qualität der im Betrieb entstehenden Schneidkante machen.

Fallstudie 8: zu Kapitel 9 Dynamische Probleme

342

Mode Number 1: 66,34 Hz

Mode Number 2: 250,95 Hz

Mode Number 3: 568,35 Hz

Mode Number 4: 781,87 Hz

Mode Number 5: 817,16 Hz

Bild 8.3:

Erste fünf Eigenschwingungsformen der Schneidwelle

343

Fallstudie 9: zu Kapitel 9.6 Erzwungene Schwingungen

Im Folgenden soll eine aus Volumen-Elementen aufgebaute Stimmgabel als repräsentatives

Beispiel für eine erzwungene Schwingung behandelt werden. Die Kraft soll durch einen

kurzen Schlag auf einen Zinken als Impuls P = 100 N für die Dauer von 1 ms aufgebracht

werden. Danach soll die Stimmgabel frei ausschwingen. Mittels einer dynamischen FEM-

Analyse wollen wir im Weiteren die Eigenschwingungsformen und das Ausschwingverhal-

ten der Stimmgabel ermitteln.

Das Eigenverhalten des Modells erhält man aus der Lösung der homogenen DGL der freien

Schwingungen

0UKÜM 

(1)

bzw. dem zugehörigen Eigenwertproblem. Die Eigenformen werden mit einer Modalanalyse

nach der Block-Lanczos-Methode ermittelt. Die Auswertung wird auf die ersten acht Eigen-

frequenzen und Eigenschwingungen beschränkt. Diese sind im Bild 9.1 dargestellt. Die erste

Eigenform (x-Richtung) hat eine Eigenfrequenz von 148,96 Hz. Die zweite Eigenform

(152,19 Hz) ist orthogonal zur ersten gerichtet. Die dritte Eigenform wird durch Torsion der

Zinken gegeneinander erzeugt. Sie tritt mit höherer Frequenz (296,36 Hz) auf. Die weiteren

ermittelten Eigenformen basieren auf den ersten dreien, weisen aber höhere Ordnungen auf.

In der nächsten Betrachtung bringen wir den Schlag am Ende eines Zinkens in x-Richtung

auf und berechnen in Zeitschritten von 0,0001 Sekunden das Schwingungsbild. In der tran-

sienten Analyse wird die Folgende inhomogene DGL mit Kraftanregung gelöst:



tPUKUCÜM 



. (2)

Der Schlag ist quantifiziert durch



.0ttP

,N100ms1tP

,00P

Da Ausschwingen erfolgen soll, berücksichtigen wir noch zusätzlich mit

KC  0001,0 (3)

0,01 % Strukturdämpfung. Am Bildschirm beobachten wir, dass vom Zeitpunkt

t aus-

gehend die Stimmgabel in x-Richtung mit der Amplitude u ausgelenkt wird und nach 0,1 s

bereits eine deutliche Abnahme der Amplitude festzustellen ist. Hierbei wurde im Wesent-

lichen die erste Eigenfrequenz angeregt.

Der Verlauf der Amplitude am Lastangriffspunkt ist im Bild 9.2

dargestellt.

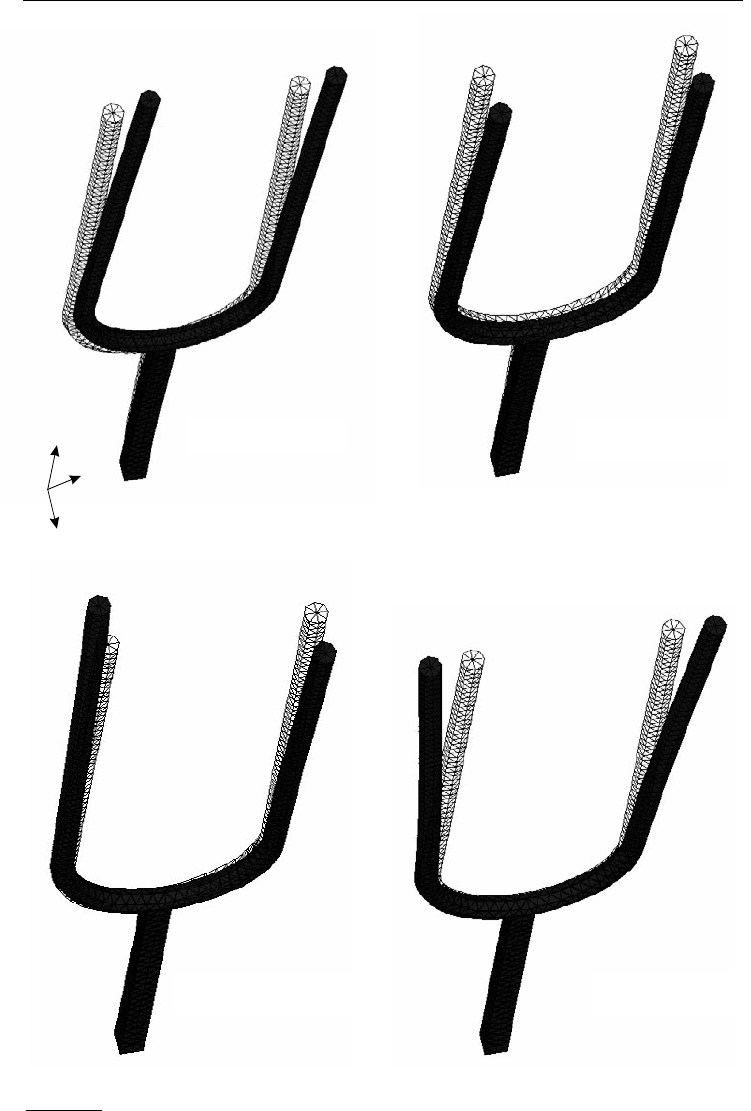
Fallstudie 9: zu Kapitel 9.6 Erzwungene Schwingungen

344

Bild 9.1a:

Die ersten vier Eigenschwingungsformen der Stimmgabel

= 148,96 Hz

n = 152,19 Hz

n = 312,94 Hz

n = 296,39 Hz

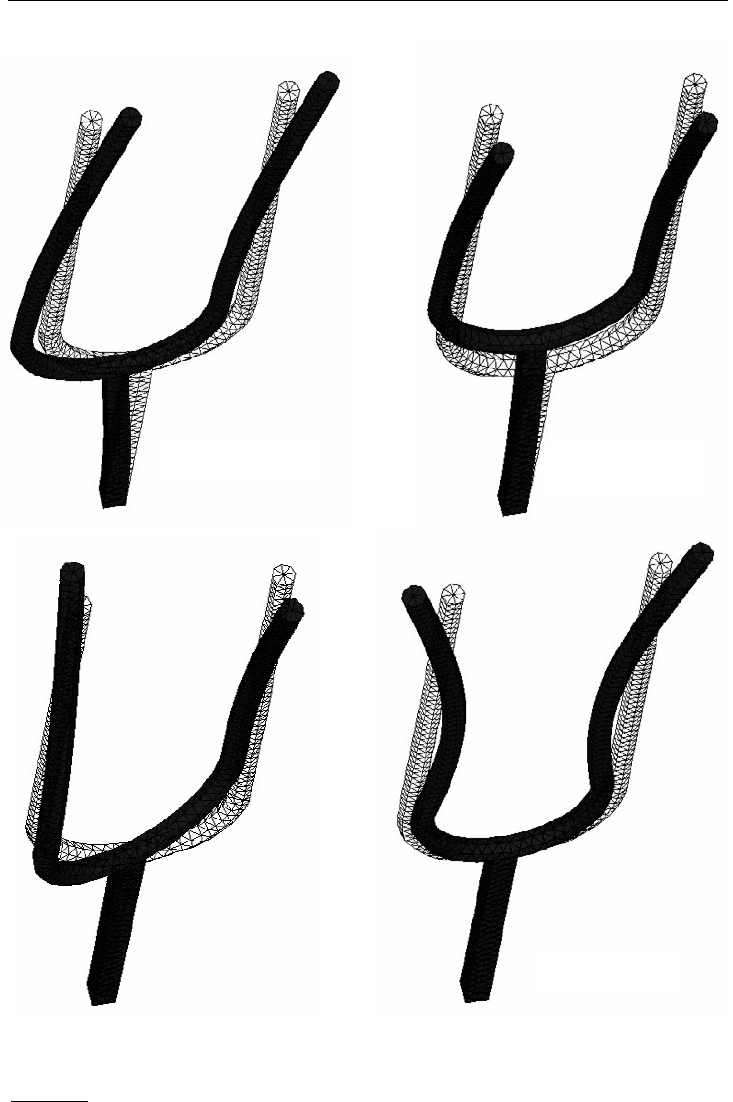
Fallstudie 9: zu Kapitel 9.6 Erzwungene Schwingungen

345

Bild 9.1b:

Die fünfte bis achte Eigenschwingungsform der Stimmgabel

n = 901,80 Hz

n = 930,54 Hz

n = 1183 Hz

n = 1880 Hz

Fallstudie 9: zu Kapitel 9.6 Erzwungene Schwingungen

346

-25

-20

-15

-10

-5

0 0,05 0,1 0,15 0,2

t (s)

(mm)

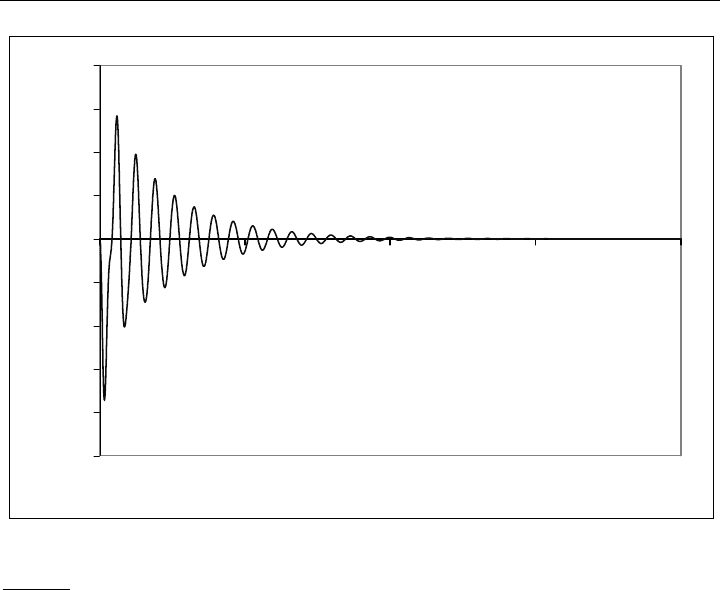
Bild 9.2: Zeitverlauf der Amplitude in x-Richtung

347

Fallstudie 10: zu Kapitel 10 Materialnichtlinearität

In den vorausgegangenen Beispielen sind alle Verformungen und Spannungsverläufe linear

elastisch analysiert worden, d. h., es wurde als Berechnungsgrundlage eine lineare Verlänge-

rung des elastischen Bereichs des Spannungs-Dehnungsdiagramms verwendet. Die Problem-

stellung wird nun dahingehend erweitert, dass ein Material gewählt werden soll, das einem

realistischen, nichtlinearen Verlauf des Spannungs-Dehnungs-Diagramms gehorcht. Bei dem

in diesem Beispiel betrachteten Bauteil handelt es sich um einen Handgriff für einen Flug-

gastsitz. Dieser Griff wird einseitig belastet und besteht aus einer MgAl-Gusslegierung und

wird im Druckgussverfahren gefertigt. Das Material hat eine Fließgrenze bzw. 0,2-%-Dehn-

grenze von

105R

2,0p

. Die Fließgrenze liegt also deutlich unterhalb der Zug-

festigkeit von

180R

, sodass ausgeprägtes Fließen des Materials anzunehmen

ist. Um Fließen aber programmtechnisch erfassen zu können, muss ein eindeutiger Zu-

sammenhang gegeben sein zwischen den von den Spannungen hervorgerufenen Dehnungen.

Zur Beschreibung dieses Zusammenhanges wählen wir das so genannte Ziegler-Prager-

Gesetz.

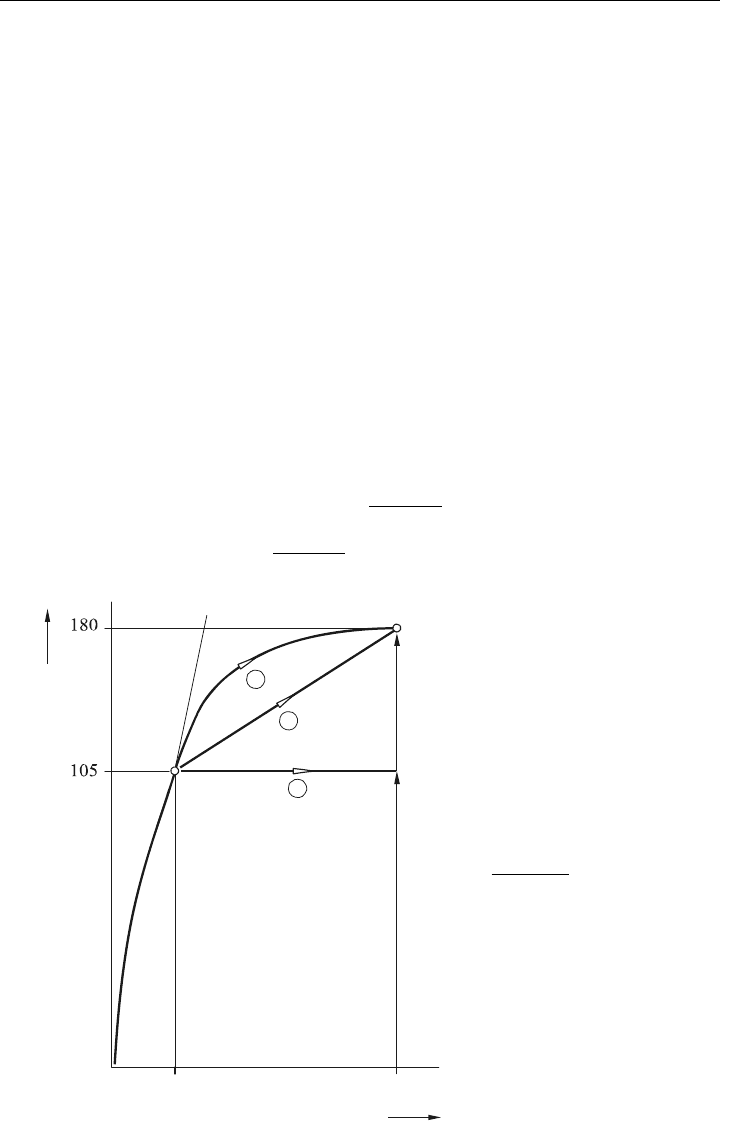
Die Strukturmechaniker Prager und Ziegler entwickelten in den 50er-Jahren Gesetzmäßig-

keiten, mit denen der Vorgang der Verfestigung bei plastischen Umformvorgängen mathe-

matisch beschrieben werden kann, siehe auch Bild 10.1. Mithilfe dieses Gesetzes wird aus

der Fließgrenze, der Bruchfestigkeit und der maximalen Bruchdehnung von 5 % ein

Materialverhalten, ähnlich dem im Bild 10.1 unter e gezeigten, generiert.

(N/mm )

0,2

5,0

H

(%)

plastischer

Bereich

elastischer

Bereich

Bild 10.1:

Spannungs-Dehnungsgesetz:

c ideal-plastisches Verhal-

ten

d Verhalten nach Prager

e Verbesserung des

Prager-Gesetzes nach

Ziegler

Klein B. FEM: Grundlagen und Anwendungen der Finite-Element-Methode im Maschinen - und Fahrzeugbau

Подождите немного. Документ загружается.