Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


201
Розділ III. Вступ до математичного аналізу
3.3.3. Нескінченно малі та нескінченно великі послідовності
Послідовність {
х
n
} називається
нескінченно малою
, якщо
lim 0
n
n
x
of
.
Послідовність {
х
n
} називається
нескінченно великою
, якщо
lim
n
n
x
of
f
.
Сума скінченого числа нескінченно малих послідовностей є не+
скінченно мала послідовність.
Добуток нескінченно малої послідовності і обмеженої є нескінчен+
но мала послідовність.
Якщо {
х
n
} нескінченно мала послідовність і
х
n
z
0, то послідовність
1
n
n
y
х
є нескінченно великою. Якщо {
у
n
} нескінченно велика по+
слідовність, то послідовність
1
n
n
x
y
є нескінченно малою послідов+
ністю.
3.3.4. Основні теореми про границі послідовності
Для того, щоб послідовність {
х
n
} мала границю
а
, необхідно і до+
статньо, щоб
x
n
= a +
n
D
, де
n
D
— нескінченно мала послідовність.
Якщо послідовності
{
х
n
} і {
у
n
} збіжні, причому
lim
n
n
xa
of
, і
lim
n
n
y
b
of
,
то:
1)
lim( ) lim lim
nn n n
nnn
xy x yab
of of of
r r r
;
2)
lim lim
nn
nn
cx c x ca
of of
;
3)
lim( ) lim lim
nn n n
nnn
xy x y ab
of of of
;
4)
lim
nof
n
n
x
y
§·
¨¸
©¹
=
lim
lim
n
n
n
n
x
y
of
of
=
a
b
, якщо
b
z
0.
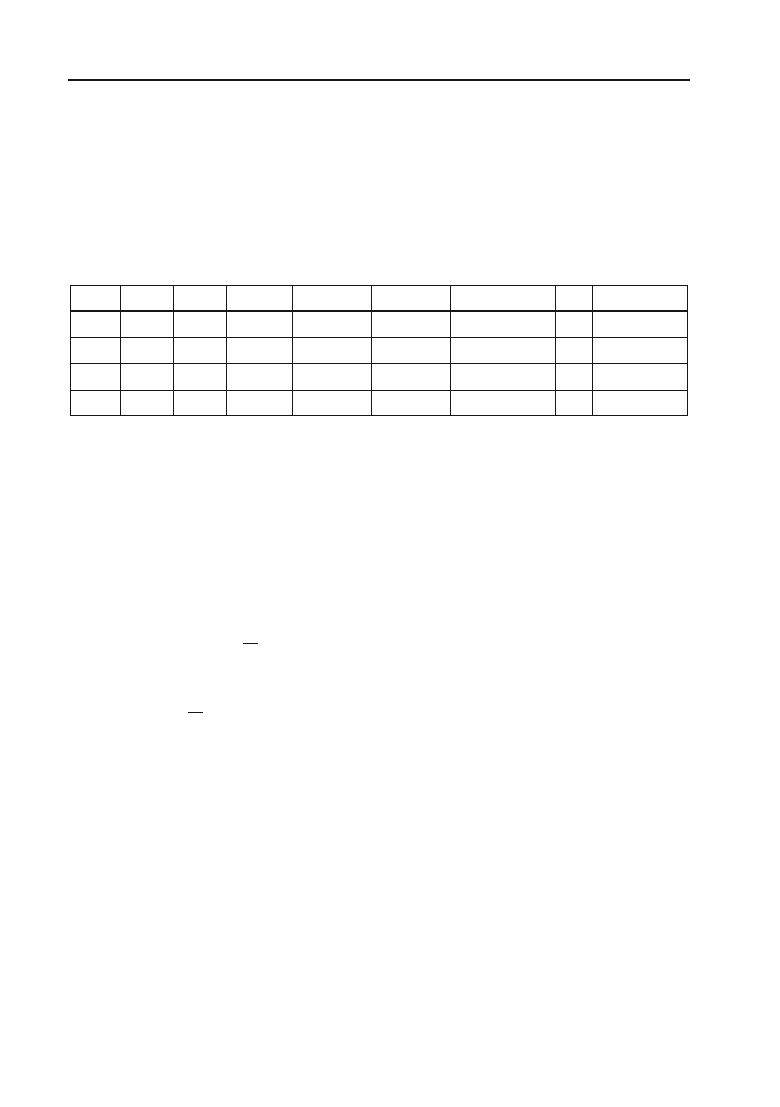
202
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
3.3.5. Розв’язання прикладів
Приклад 3.44.
Надаючи
n
значень 0, 1, 2, 3, 4, 5, ... ,
скласти табли+
цю значень змінних
x
n
=
1 + 0,1
–n
;
y
n
=
–0,1
n
;
z
n
=
(–0,1)
n
;
u
n
=
(–1)
n
+
+
0,1
n
і визначити характер їх зміни при необмеженому зростанні
n
,
тобто
n of
.
Розв’язок.
Обчислимо значення заданих змінних при вказаних
загальних
n
, одержуємо наступну таблицю:
Із цієї таблиці видно:
1) Із збільшенням
n
послідовні значення змінної {
х
n
} наближа+
ються до одиниці так, що при достатньо великому
n
абсолютне зна+
чення їх різниці
|x
n
–
1
|
буде менше будь+якого наперед заданого
додатного числа
H
, яким би малим воно не було.
Це можна і довести. Нехай задано число
0
H
!
. Покладаючи
|x
n
–
1
| =
0,1
n
<
H
, знаходимо, логарифмуючи обидві частини не+
рівності, що
n >
1
lg
H
, тобто
|x
n
–
1
|
буде менше
H
, як тільки
n
стане
більше за
1
lg
H
. Отже, згідно означенню границі послідовності, по+
слідовність {
х
n
} має границю, рівну 1,
lim 1
n
n
x
of
, до якого вона пря+
мує справа залишаючись більше її, тобто монотонно спадаючи.
2) Послідовні значення змінної {
у
n
} з збільшенням
n
необмежено
спадають так, що при достатньо великому
n
вони за абсолютним
значенням будуть більше будь+якого заданого додатного числа
М
, яке
б великим воно не було. Доведемо це. Нехай задано число
М >
0.
Покладаючи |
y
n
| =
0,1
–n
>
M
, знаходимо, логарифмуючи обидві час+
тини нерівності, що
n
> lg
M
, тобто |
y
n
|
буде більше
М
, як тільки
n
стане більше за
lg
M
. Отже, згідно з означенням нескінченно великої
послідовностей, послідовність {
у
n
} є нескінченно велика величина:
n 0 1 2 3 4 5 …
n of
x
n
2 1,1 1,01 1,0001 1,0001 1,00001
…х
o
1+0
y
n
–1 –10 –100 –1000 –10000 –100000
…у
o
f
z
n
1 –0,1 0,01 –0,001 0,0001 –0,00001
…z
o
0
u
n
2 –0,9 1,01 –0,999 0,0001 –0,99999
…
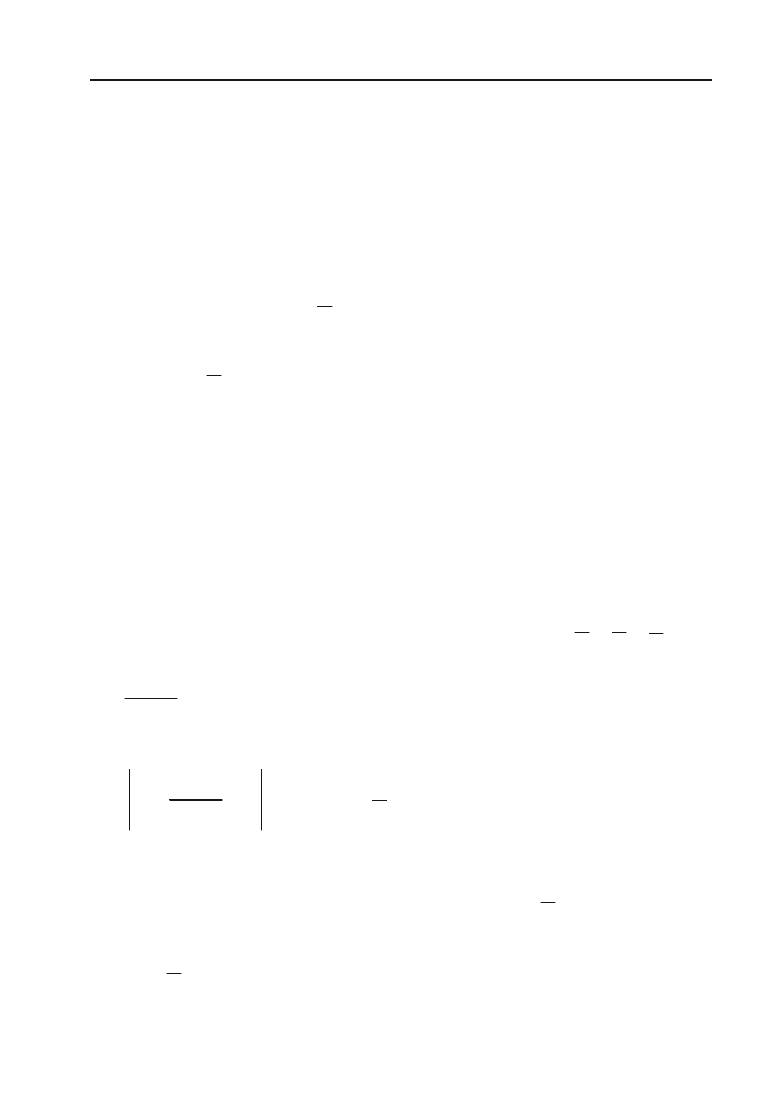
203
Розділ III. Вступ до математичного аналізу
lim
n
n
y
of
f
.
3) Зі збільшенням
n
послідовні значення змінної
z
n
наближають+
ся до нуля так, що при достатньо великому
n
вони по абсолютному
значенню будуть менші будь+якого наперед заданого числа
e
, яким
би малим воно не було. Доведемо це. Нехай задане число
0
H
!
.
Покладаючи
|z
n
| =
0,1
n
<
H
, знаходимо, логарифмуючи обидві части+
ни нерівності, що
n >
1
l
g
H
, тобто
|z
n
|
буде менше , як тільки
n
стане
більше за
1
l
g
H
. Отже, згідно означення нескінченно малої послідов+
ності, послідовність
z
n
є нескінченно мала послідовність:
lim 0
n
n
z
of
.
Вона прямує до своєї границі – нулю, коливаючись біля нього.
4) Послідовні значення змінної
u
n
з збільшенням
n
не наближа+
ються ні до якого визначеного числа. Через це послідовність {
u
n
} не
має границі. Вона не є і нескінченно великою, так як її значення не
зростають необмежено разом з зростанням
n
. Послідовність {
u
n
} —
обмежена.
Приклад 3.45.
Довести, що послідовність 0,
3
2
,
2
3
,
5
4
,
... ,
(1+
(1)
n
n
),
...
має
lim 1
n
n
a
of
.
Розв’язання
. Нехай, наприклад,
H
= 0,1. Тоді нерівність
|a
n
– 1|<0,1
або
(1)
(1 ) 1
n
n
H
. Тобто
1
n
H
виконується при
n
>10. Анало+
гічно для
H
=
0,01
|a
n
–
1
|<
0,01 при
n
>100.
Для кожного
H
>0 нерівність
|a
n
–
1
|<
H
або
1
n
H
виконується
при
n >
1
H
.
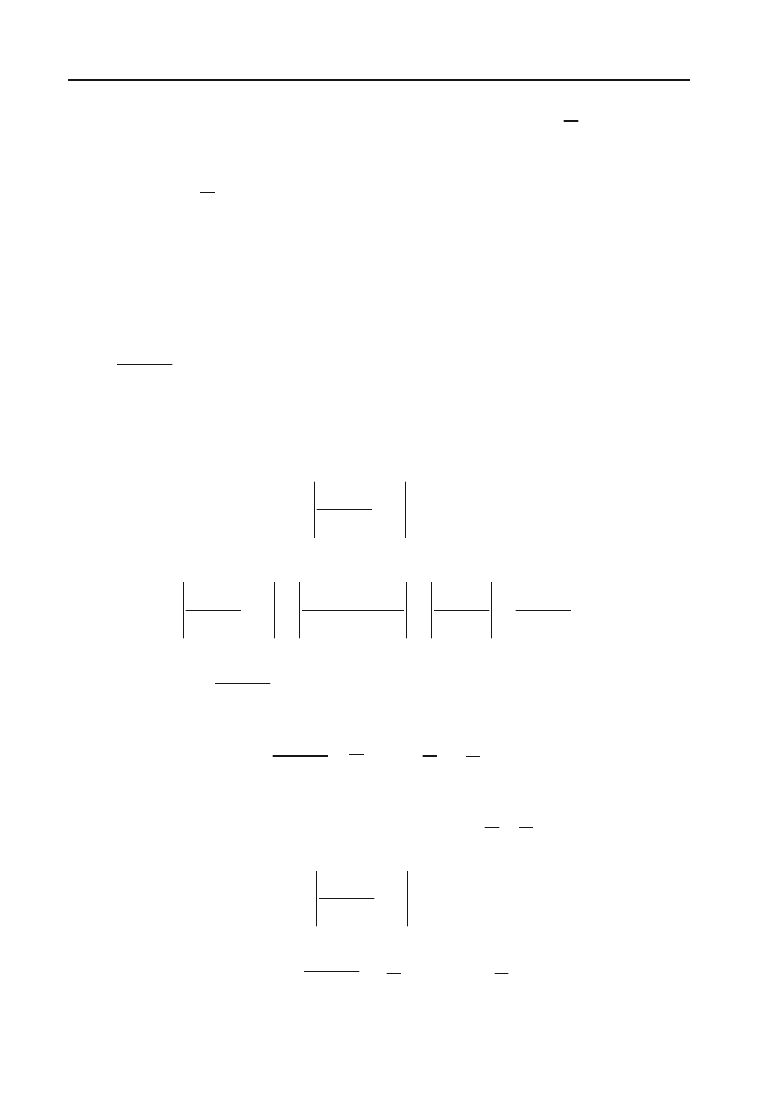
204
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Отже, при будь+якому
0
H
!
існує такий номер
N =
1
H
(або рівний
цілій частині
1
H
), що для всіх
n >N
(при
H
= 0,1
для
n >
10, при
H
=
0,01
для
n >
100 і т.д.) виконується нерівність
|a
n
–
1
|<
H
, а це
означає, що
lim 1
n
n
a
of
.
Приклад 3.46.
Довести, що послідовність з загальним членом
4
21
n
n
x
n
має границю, рівну 2
.
Розв’язок.
Виберемо довільно додатне число
H
і покажемо, що
для нього можна підібрати таке число
N
, що для всіх значень номера
n
більшого цього числа
N
, буде виконуватися нерівність:
4
2
21
n
n
H
.
Перетворимо вираз
444222
2
21 21 2121
nnn
nnnn
.
Одержуємо
2
21n
H
. Звідси слідує, що
21
2
n
>
1
H
,
n >
1
H
–
1
2
.
Таким чином, якщо номер
n
більше, ніж
1
H
–
1
2
, то нерівність
4
2
21
n
n
H
.
Нехай
H
=
0,005,
n >
1
0,005
–
1
2
=
200 –
1
2
.
N =
199.

205
Розділ III. Вступ до математичного аналізу
Отже, для всіх номерів більших, ніж 199 при
H
=
0,005, буде
виконуватися нерівність
4
2
21
n
n
H
. Починаючи з 200 члену всі
члени послідовності будуть знаходитись в інтервалі (2 –
1
200
; 2
+
1
200
),
тобто в інтервалі (1,995; 2005).
Таким чином,
lim
nof
4
2
21
n
n
.
Приклад 3.47.
Користуючись означенням границі послідовності,
довести, що послідовність з загальним членом
1
(1)
n
n
x
n
має гра+
ницю рівну нулю.
Розв’язок.
Запишемо ряд членів послідовності:
1,
1
2
,
1
3
,
1
4
,
1
5
,
1
6
, ...
Знайдемо вираз для члена
N
в залежності від
H
. Для будь+якого
n >N
маємо
1
(1)
0
n
n
H
, або
1
n
H
.
Розв’язавши нерівність відносно
n
, одержуємо
1
n
H
!
. Отже, за
N
можна брати число
1
H
(або будь+яке більше число). Таким чином,
для будь+якого
0
H
!
існує таке число
N =
1
H
ªº
«»
¬¼
, що при
n > N =
1
H
виконується нерівність
1
(1)
0
n
n
H
. Це означає, що границею
заданої послідовності є число нуль.
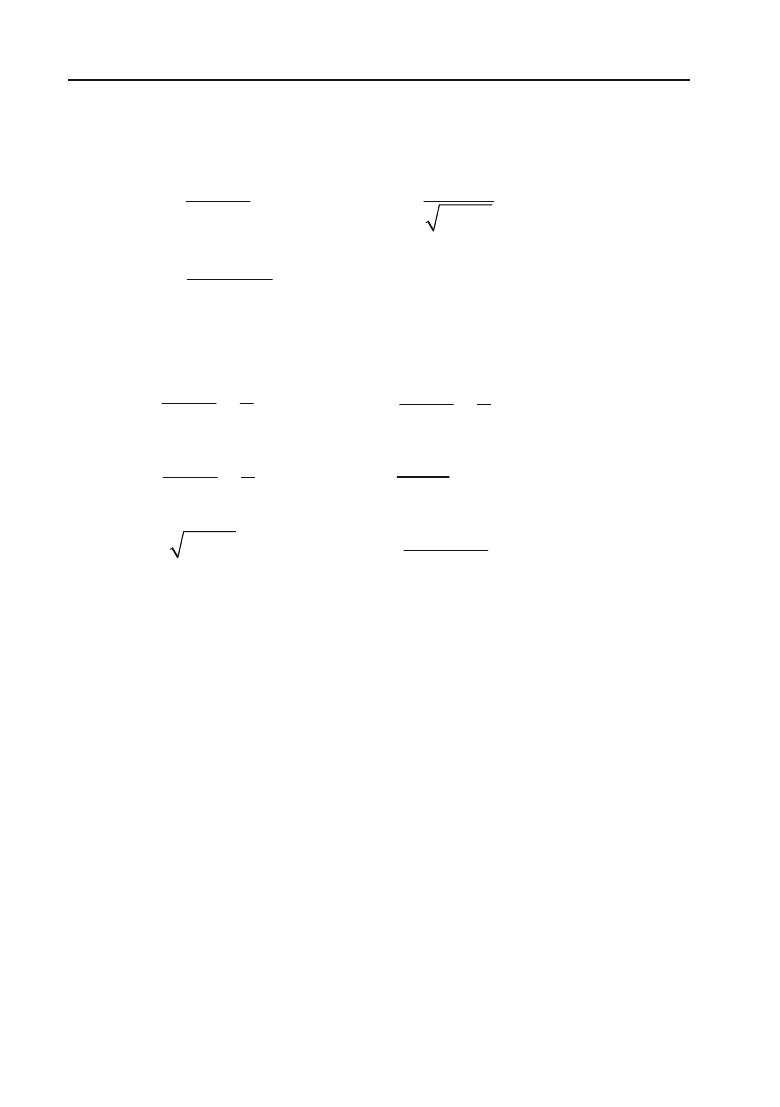
206
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
3.3.6. Приклади для самостійного розв’язку
3.48.
Довести обмеженість послідовностей:
а) {
u
n
}
=
2
2
21
2
n
n
;б) {
u
n
}
=
2
1
1
n
n
;
в) {
u
n
}
=
(1)
31
n
n
n
.
3.49.
Користуючись визначенням границі послідовності, довести,
що:
а)
11
lim
212
n
n
n
of
;б)
1
lim
212
n
n
n
of
;
в)
55
lim
212
n
n
n
of
;г)
21
lim 1
2
n
n
n
of
;
д)
2
lim( 1 ) 0
n
nn
of
;ж)
2(1)
lim 0
n
n
n
of
.

207
Розділ III. Вступ до математичного аналізу
§3.4. Границя функції. Особливості границі.
Розкриття невизначеностей.
Перша та друга визначні границі.
3.4.1. Означення границь змінної
Стале число
а
називається
границею змінної величини х
, якщо
для будь+якого наперед заданого числа
0
H
!
можна вказати таке
значення змінної
х
, що всі наступні значення змінної будуть задо+
вольняти нерівності |
x – a| <
H
.
Якщо число
а
є границею змінної величини
х
, то говорять, що
х
прямує до границі
а
, і пишуть
х
o
а
або lim
x = a
.
Границя сталої дорівнює самій сталій, тобто lim
с = с
. Із визна+
чення границі змінної слідує, що змінна величина не може мати двох
границь, це число єдине.
Не слід вважати, що кожна змінна величина має границю. Є змінні
величини, які не прямують до границі.
3.4.2. Поняття границі функції
Границею функції y = f(x) при х, що прямує до а
, називаєть+
ся число
b
, якщо для будь+якого
0
H
!
існує число
0
G
!
, таке, що
для всіх
х
, які задовольняють нерівність 0
< |x – a| <
G
випливає
|f
(
x
)
– b| <
H
.
Позначення:
lim ( )
xa
fx b
o
.
Якщо
f
(
x
)
o
b
при
х а
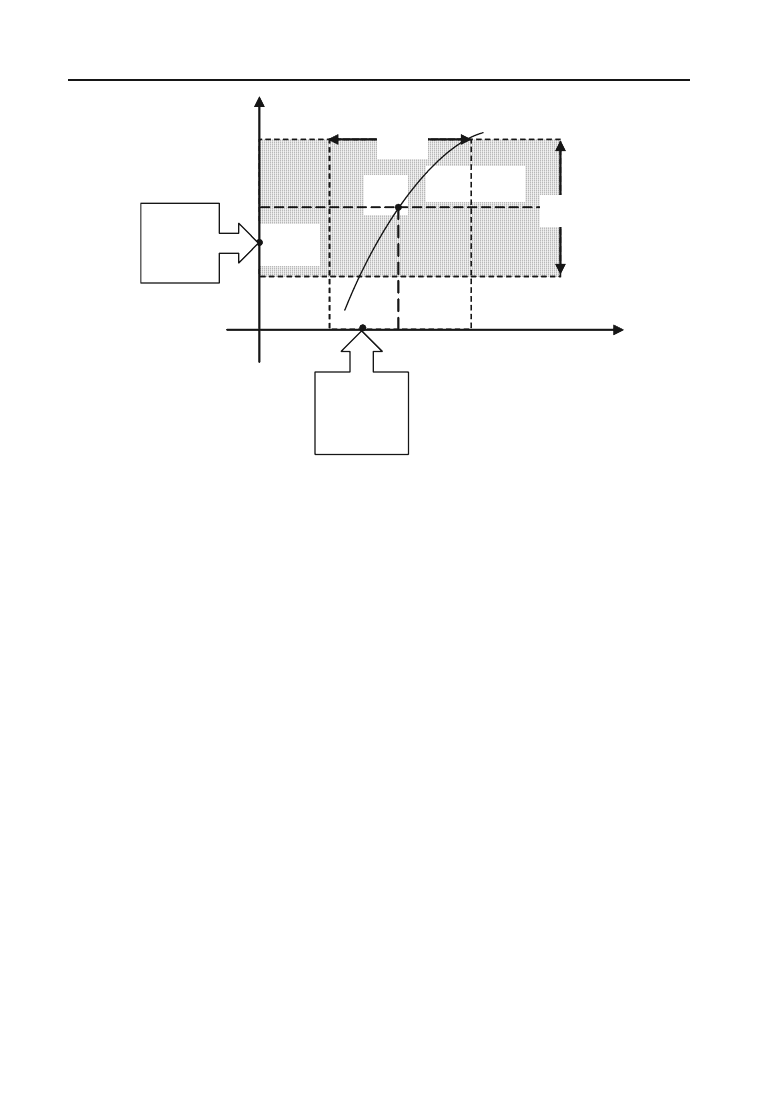
, то на графіку функції
y = f
(
x
)
це ілю+
струється таким чином (рис. 3.33): так як із нерівності
|x – a| <
G
слідує нерівність
|f
(
x
)
– b| <
H
, то це означає, що для всіх точок
х
,
які віддалені від точки
а
не далі ніж на
G
, точки
М
графіка функцій
y = f
(
x
) лежать всередині смуги шириною
2
H
, що обмежена прями+
ми
y = b –
H
i
y = b +
H
.
Правою границею функції
y = f
(
x
), коли
х
прямує до
а
справа,
називається число
b
2
, таке, що при будь+якому
0
H
!
існує число
0
G
!
,
208
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
при якому для всіх
х
, що задовольняють нерівності
а < x < а +
G
маємо
|f
(
x
)
– b
2
| <
H
.
Позначається:
2
0
lim ( )
xa
fx b
o
.
Лівою границею функції
y = f
(
x
), коли
х
прямує до
а
зліва, нази+
вається число
b
1
, таке, що при будь+якому
0
H
!
існує число
0
G
!
,
при якому для всіх
х
, що задовольняють нерівності
а –
G
< x < а
маємо
|f
(
x
)
– b
1
| <
H
.
Позначається:
1
0
lim ( )
xa
f
xb
o
.
Інколи границею
lim ( )
xa
f
xb
o
називають
двосторонньою грани
ц
ею, а границі зліва та справа —
односторонніми границями
.
Зв’язок між односторонніми та двосторонньою границями
.
Функція
y = f
(
x
) має границю в точці
х = а
тоді і тільки тоді, коли
існують границі зліва і справа в точці
х = а
і дорівнюють одна одній:
00
lim
()
lim
()
lim
()
xa xa xa
f
x
f
x
f
x
ooo
.
M
y = f(x)
2
G
2
H
f(x)
0 a–
G
a a+
G
X
Y
b+
H
b
b–
H
усі х=а
лежать
тут
f(x)
лежать
тут
Рис. 3.33.

209
Розділ III. Вступ до математичного аналізу
3.4.3. Теореми про границі функції
1. Якщо
lim ( )
xa
f
xb
o
, то функція
f(x)
обмежена при
х
o
а
.
2. Якщо
lim ( )
xa
fx b
o
,
0b z
, то знайдеться такий
G
+окіл точки,
де ця функція набуває значень, які мають тай самий знак, що і
b
.
3. Якщо
f
(
x
)
= С
, то
lim ( )
xa
f
xC
o
.
4. Якщо
() () ()
x
fx x
M
\
dd
і
lim ( ) lim ( )
xa xa
xxb
M
\
oo
, то існує
границя
lim ( )
xa
f
xb
o
.
5. Якщо існують границі
lim ( )
xa
x
A
M
o
,
lim ( )
xa
x
B
\
o
, то вико+
нуються такі співвідношення:
1)
lim( ( ) ( )) lim ( ) lim ( )
xa xa xa
xx x xAB
M\ M \
ooo
;
2)
lim( ( ) ( )) lim ( ) lim ( )
xa xa xa
xx x xAB
M\ M \
ooo
;
3)
lim
x
ao
()
()
x
x
M
\
=
lim ( )
lim ( )
xa
xa
x
x
M
\
o
o
=
A
B
, якщо
0B z
.
3.4.4. Перша і друга визначні границі
Перша визначна границя:
0
lim
xo
sin x
x
= 1.
Наслідки:
1)
0
lim
xo
sin
sin
ax
bx
=
a
b
;
2)
0
lim
xo
tg ax
bx
=
a
b
;
210
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
3.4.5. Розв’язання прикладів
Границя функції не залежить від того, чи визначена функція в
граничній точці, чи ні. Але ця умова має істотне значення при зна+
ходженні границь функції:
а) Якщо функція є елементарною і якщо значення аргументу
належить її області визначення, то обчислення границі функції зво+
диться до простої підстановки граничного значення аргументу, так
як границя елементарної функції
f
(
x
) при
х
, що прямує до значення
а
, яке входить в область її визначення, дорівнює значенню функції
при
х = а
, тобто
lim ( ) ( )
xa
f
xfa
o
.
3)
0
lim
xo
arctgax
bx
=
a
b
.
Друга визначна границя
lim
xof
1
1
x
x
§·
¨¸
©¹
=
е
.
Наслідки:
1)
0
lim
xo
1
(
1
)
D
D
=
е
;
2)
lim
xof
1
1
x
x
§·
¨¸
©¹
=
1
e
;
3)
0
lim
xo
1
(1 )
D
D
=
1
e
;
4)
lim
xof
1
x
k
x
§·
¨¸
©¹
=
е
k
.
5)
0
lim
xo
1
(1 )k
D
D
=
е
k
.
Число
е
— ірраціональне:
е =
2,7182818... Логарифм за основою
е
називається
натуральним логарифмом
і позначається ln.
