Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

211
Розділ III. Вступ до математичного аналізу
Приклад 3.50.
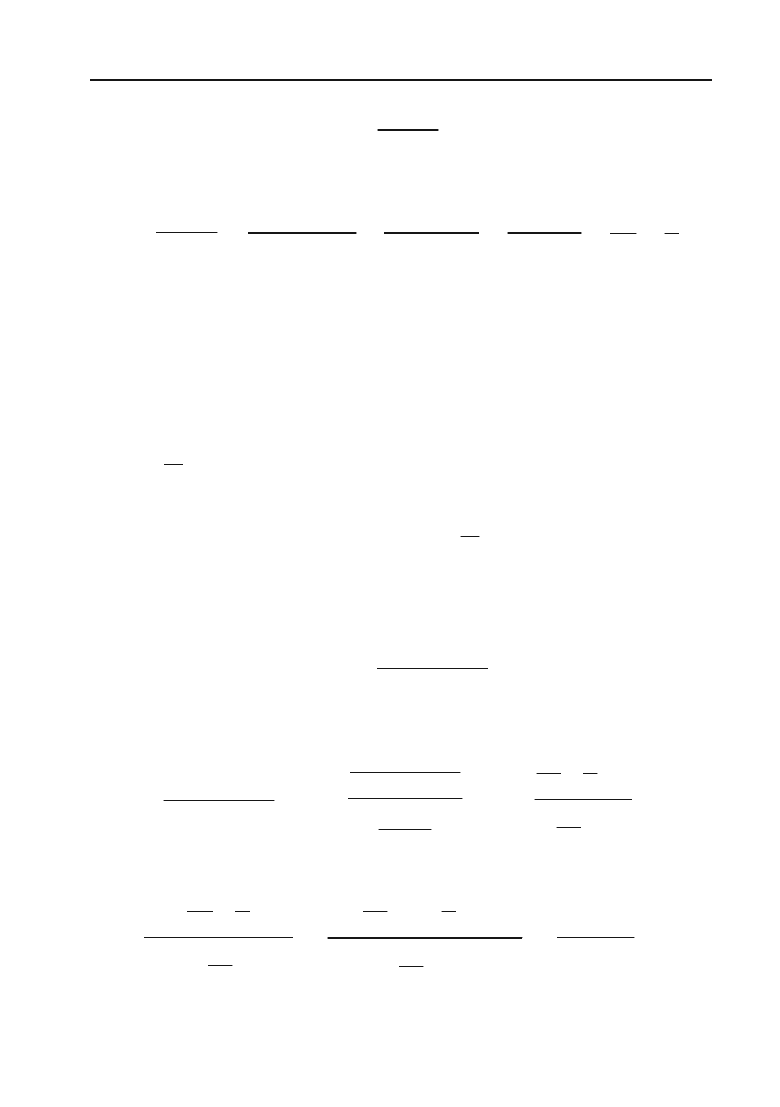
Знайти
3
lim
xo
23
37
x
x
.
Розв’язок.
За теоремами про границі маємо:
3
lim
xo
23
37
x
x
=
3
3
lim
(
23
)
lim
(
37
)
x
x
x
x
o
o
=
3
3
2lim 3
37lim
x
x
x
x
o
o
=
23 3
373
=
3
24
=
1
8
.
б)
Якщо аргумент прямує до нескінченості або до числа, яке не
належить області визначення функції, то в кожному із таких випадків
для знаходження границь функції необхідні спеціальні дослідження.
І.
Випадок, коли при
x
of
або
x
a
o
функція представляє
собою відношення двох нескінченно великих величин (невизна+
ченість
f
f
).
При розкритті невизначеності виду
f
½
®¾
f
¯¿
поступають так: чисель+
ник і знаменник дробу ділять на найвищий степінь змінної, який
зустрічається в членах дробу.
Приклад 3.51.
Знайти
lim
nof
2
2
13 2
1
nn
n
.
Розв’язок.
lim
nof
2
2
13 2
1
nn
n
=
lim
nof
2
2
2
2
13 2
1
nn
n
n
n
=
lim
nof
2
2
13
2
1
1
nn
n
=
=
2
2
13
lim
(
2
)
1
lim
(
1
)
n
n
nn
n
of
of
=
2
2
13
lim lim lim2
1
lim lim1
nnn
nn
nn
n
of of of
of of
=
002
01
= –2.
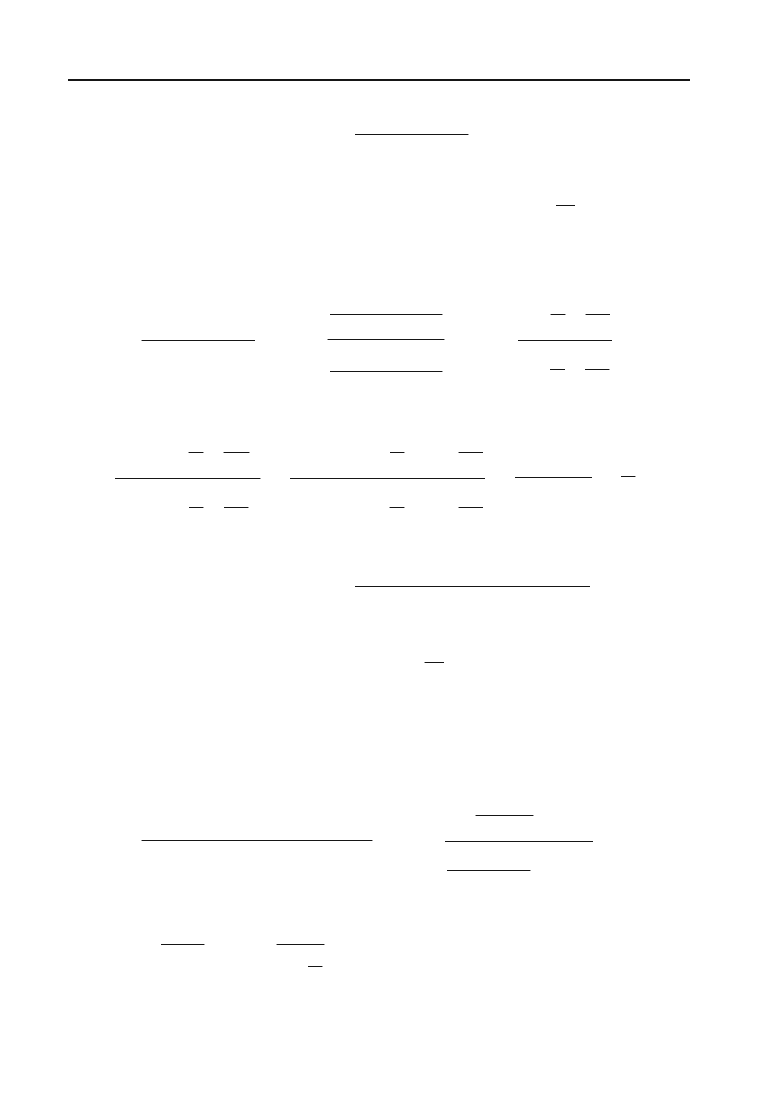
212
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Приклад 3.52.
Знайти
lim
nof
2
2
923
574
nn
nn
.
Розв’язок.
Переконавшись, що маємо випадок
f
½
®¾
f
¯¿
, поділимо
чисельник і знаменник на
n
2
(найвищий степінь
n
). Знаходимо:
lim
nof
2
2
923
574
nn
nn
=
lim
nof
2
2
2
2
923
574
nn
n
nn
n
=
lim
nof
2
2
23
9
74
5
n
n
nn
=
=
2
2
23
lim
(
9
)
74
lim
(
5
)
n
n
nn
nn
of
of
=
2
2
23
lim9 lim lim
74
lim5 lim lim
nn n
nn n
nn
nn
of of of
of of of
=
900
500
=
9
5
= 1,8
.
Приклад 3.53.
Знайти
lim
nof
2468...2
1 3 5 7 ... (2 1)
n
n
.
Розв’язок.
Маємо невизначеність
f
½
®¾
f
¯¿
. Тут чисельник дробу є
сума
n
членів арифметичної прогресії, а знаменник є сума (
n
+ 1)
членів другої арифметичної прогресії. Перетворюємо ці прогресії за
відомими формулами. Одержуємо:
lim
nof
2468...2
1 3 5 7 ...
(
21
)
n
n
=
lim
nof
22
2
12 1
(
1
)
2
n
n
n
n
=
=
lim
nof
1
n
n
=
lim
nof
1
1
1
n
= 1.
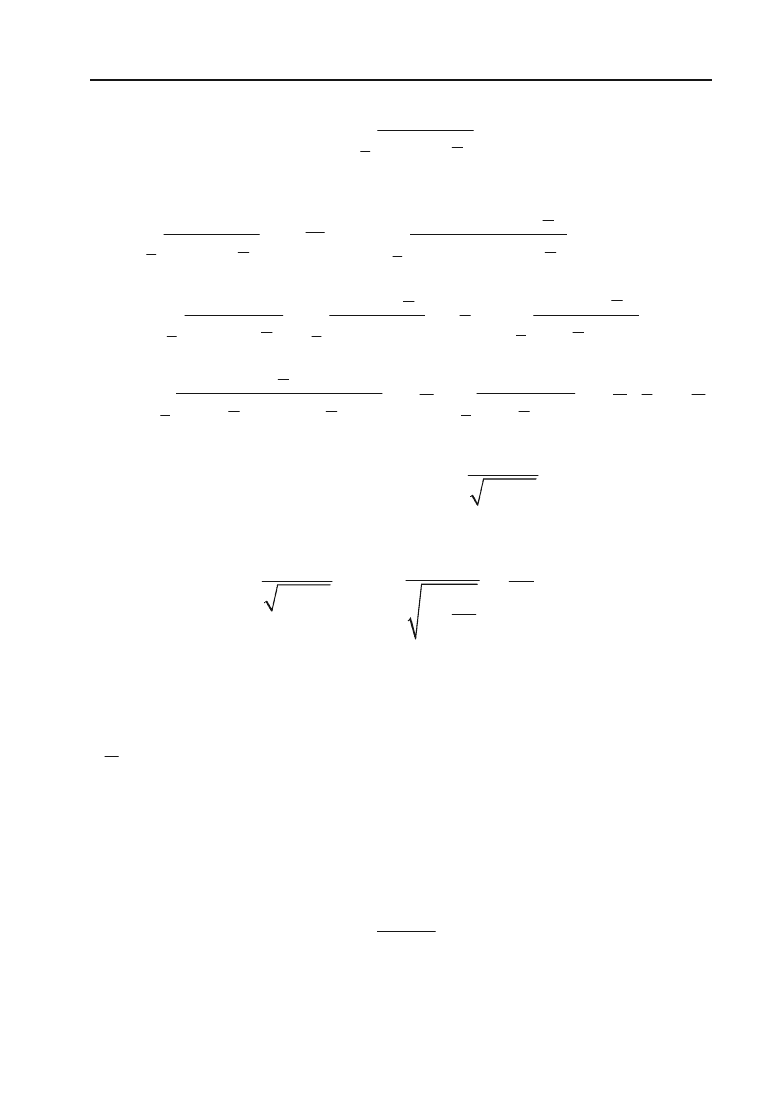
213
Розділ III. Вступ до математичного аналізу
Приклад 3.54.
Знайти
4
lim
x
S
o
4
tg2
ctg( )
x
x
S
.
Розв’язок.
4
lim
x
S
o
4
tg2
ct
g( )
x
x
S
=
f
½
®¾
f
¯¿
=
4
lim
x
S
o
4
4
sin2 sin
()
cos2 cos
()
xx
xx
S
S
=
=
4
lim
x
S
o
4
sin2
cos
()
x
x
S
4
lim
x
S
o
4
sin( )
cos2
x
x
S
=
1
1
4
lim
x
S
o
4
2
sin
()
sin
(
2
)
x
x
S
S
=
=
4
lim
x
S
o
4
44
sin( )
2sin( )cos( )
x
xx
S
SS
=
1
2
4
lim
x
S
o
4
1
cos( )x
S
=
1
2
1
1
=
1
2
.
Приклад 3.55.
Знайти границю
lim
nof
2
1
n
n
.
Розв’язок.
Поділимо чисельник і знаменник на
n
, одержуємо:
lim
nof
2
1
n
n
=
lim
nof
2
1
1
1
n
=
1
1
= –1.
ІІ.
Випадок, коли при
x
of
або
x
a
o
функція представляє
собою відношення двох нескінченно малих величин (невизначеність
0
0
½
®¾
¯¿
).
Якщо знаходиться границя дробу, чисельник і знаменник якого
многочлени, які в граничній точці перетворюється в нуль, то згідно
теореми Безу обидва многочлени розділяться без залишку на
х – а
,
тобто такий дріб можна скоротити на
х – а
.
Приклад 3.56.
Знайти
2
lim
xo
2
2
4
x
x
.
Розв’язок.
Спочатку переконаємося, що границю функції не мож+
на знайти безпосередньо підстановкою змінної. Що при вказаному
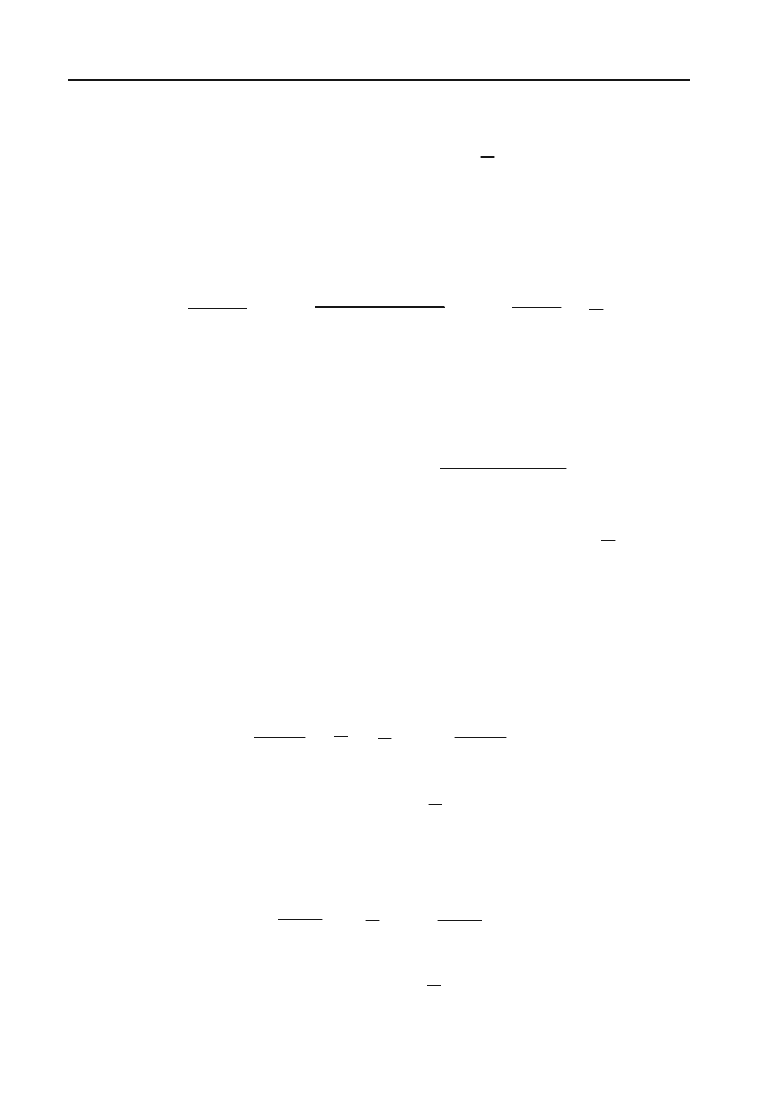
214
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
значенні змінної аргументу вона представляє відношення двох не+
скінченно малих величин (невизначеність
0
0
½
®¾
¯¿
). Виконуємо пере+
творення щоб скоротити дріб на множник, який прямує до нуля.
Розкладаємо знаменник дробу на множини (
х
– 2)(
х
+ 2) і ско+
рочуємо дріб на (
х
– 2).
2
lim
xo
2
2
4
x
x
=
2
lim
xo
2
(
2
)(
2
)
x
xx
=
2
lim
xo
1
2x
=
1
4
.
Тут немає скорочення на нуль, що недопустимо.
Згідно визначення границі функції аргумент
х
прямує до свого
граничного значення 2, і ніколи з ним не співпадає. Через це
х –
2
z
0
.
Приклад 3.57.
Знайти границю
5
lim
xo
2
2
2115
3145
xx
xx
.
Розв’язок.
Переконавшись, що маємо невизначеність
0
0
½
®¾
¯¿
, розк+
ладаємо чисельник і знаменник дробу на множини, як квадратний
тричлен, за формулою
ax
2
+ bx + c = a
(
x – x
1
)(
x – x
2
), де
х
1
і
х
2
—
корні тричлена.
2
х
2
–
11
х +
5 = 0,
D =
11
2
– 4
2
5 = 121 – 40 = 81,
x
1
=
11 9
4
=
2
4
=
1
2
,
x
2
=
11 9
4
=
5
.
2
х
2
–
11
х +
5 = 2(
x –
1
2
)(
x
– 5).
3
x
2
–
14
x
– 5 = 0,
D =
7
2
+ 3
5 = 64,
x
1
=
78
3
=
1
3
,
x
2
=
78
3
=
5.
3
x
2
– 14
x –
5 = 3(
x +
1
3
)(
x –
5).

215
Розділ III. Вступ до математичного аналізу
Потім скорочуємо дріб на (
х –
5):
5
lim
xo
2
2
2115
3145
xx
xx
=
5
lim
xo
1
2
1
3
2
()(
5
)
3
()(
5
)
xx
xx
=
5
lim
xo
21
31
x
x
=
5
16
.
Приклад 3.58.
Знайти границю
lim
x
S
o
2
3
sin
1cos
x
x
.
Розв’язок
.
lim
x
S
o
2
3
sin
1cos
x
x
=
lim
x
S
o
2
2
1cos
(
1cos
)(
1cos cos
)
x
x
xx
=
=
lim
x
S
o
2
(1 cos )(1 cos )
(
1cos
)(
1cos cos
)
xx
x
xx
=
lim
x
S
o
2
(1 cos )
(1 cos cos )
x
xx
=
=
11
111
=
2
3
.
Приклад 3.59.
Знайти границю
0
lim
xo
11x
x
.
Розв’язок.
З’ясувавши спочатку, що при вказаному значенні аргу+
менту задана функція перетворюється в відношення двох нескінчен+
но малих величин (випадок
0
0
½
®¾
¯¿
), перетворимо дріб таким чином,
щоб скоротити її на множник, який прямує до нуля. Знищимо ірра+
ціональність в чисельнику шляхом помноження чисельника і зна+
менника на (1
+
1
x
), а потім скоротимо дріб на
х
:
0
lim
xo
11
x
x
=
0
lim
xo
(1 1)(1 1)
(1 1)
xx
xx
=
=
0
lim
xo
1
(
1
)
(
11
)
x
xx
=
0
lim
xo
(
11
)
x
xx
=
0
lim
xo
1
11x
=
1
2
.
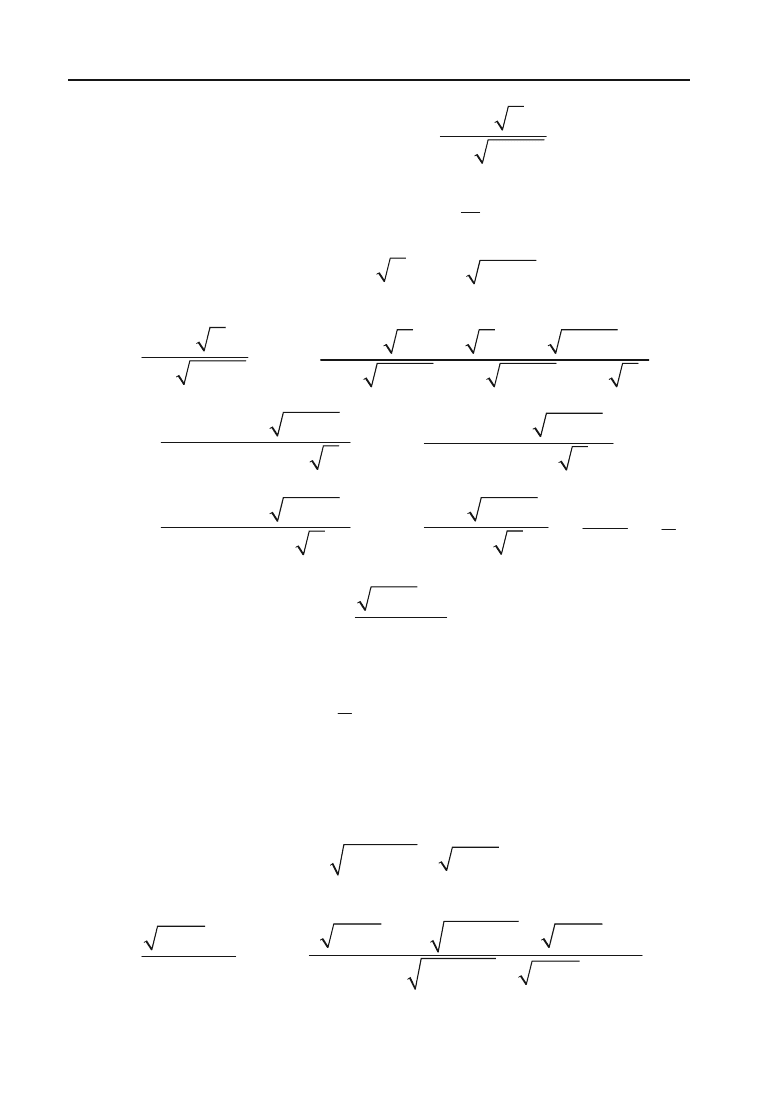
216
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Приклад 3.60.
Знайти границю
4
lim
xo
2
321
x
x
.
Розв’язок.
Маємо невизначеність виду
f
½
®¾
f
¯¿
. Помножимо чисель+
ник і знаменник на добуток (2 +
x
)(3 +
21
x
), а потім скоро+
тимо дріб на 4 –
х
:
4
lim
xo
2
321
x
x
=
4
lim
xo
(
2
)(
2
)(
321
)
(
321
)(
321
)(
2
)
xx x
x
xx
=
=
4
lim
xo
(
4
)(
321
)
(
92 1
)(
2
)
xx
x
x
=
4
lim
xo
(4 )(3 2 1)
(8 2 )(2 )
xx
xx
=
=
4
lim
xo
(
4
)(
321
)
2
(
4
)(
2
)
xx
x
x
=
4
lim
xo
(3 2 1)
2(2 )
x
x
=
33
24
=
3
4
.
Приклад 3.61.
Знайти
7
lim
xo
3
61
7
x
x
.
Розв’язок.
Тут і границя чисельника і знаменника дорівнює нулю,
тобто маємо невизначеність
0
0
½
®¾
¯¿
. Перенесемо ірраціональність із чи+
сельника в знаменник. Скористуємося відомою формулою алгебри
(
а – b
)(
a
2
+ ab + b
2
)
=
a
3
– b
3
.
Отже, для того, щоб одержати в чисельнику різницю кубів, необ+
хідно його помножити на
2
3
3
(6) 61xx
. Помноживши і
знаменник на цю величину, одержуємо:
7
lim
xo
3
61
7
x
x
=
7
lim
xo
2
33
3
2
3
3
(
61
)( (
6
)
61
)
(
7
)( (
6
)
61
)
xxx
xx x
=
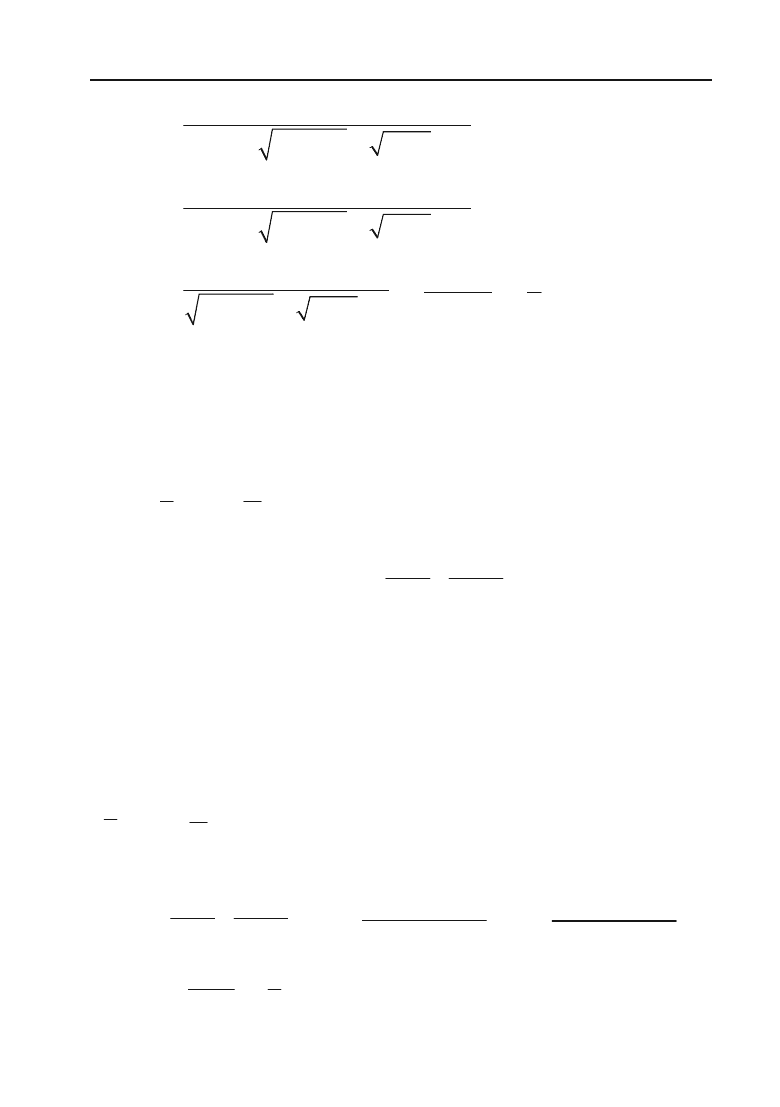
217
Розділ III. Вступ до математичного аналізу
=
7
lim
xo
2
3
3
61
(
7
)( (
6
)
61
)
x
xx x
=
=
7
lim
xo
2
3
3
7
(
7
)( (
6
)
61
)
x
xx x
=
=
7
lim
xo
2
3
3
1
(6) 61xx
=
1
111
=
1
3
.
ІІІ.
Випадок, коли при
x
a
o
або
x
of
функція
f
(
x
) представ+
ляє різницю двох додатних нескінченно великих величин (випадок
{
;
}
ff
).
Цей випадок знаходження границі функції можна привести до ви+
падку
0
0
½
®¾
¯¿
або
f
½
®¾
f
¯¿
шляхом перетворення функції до вигляду дробу.
Приклад 3.62.
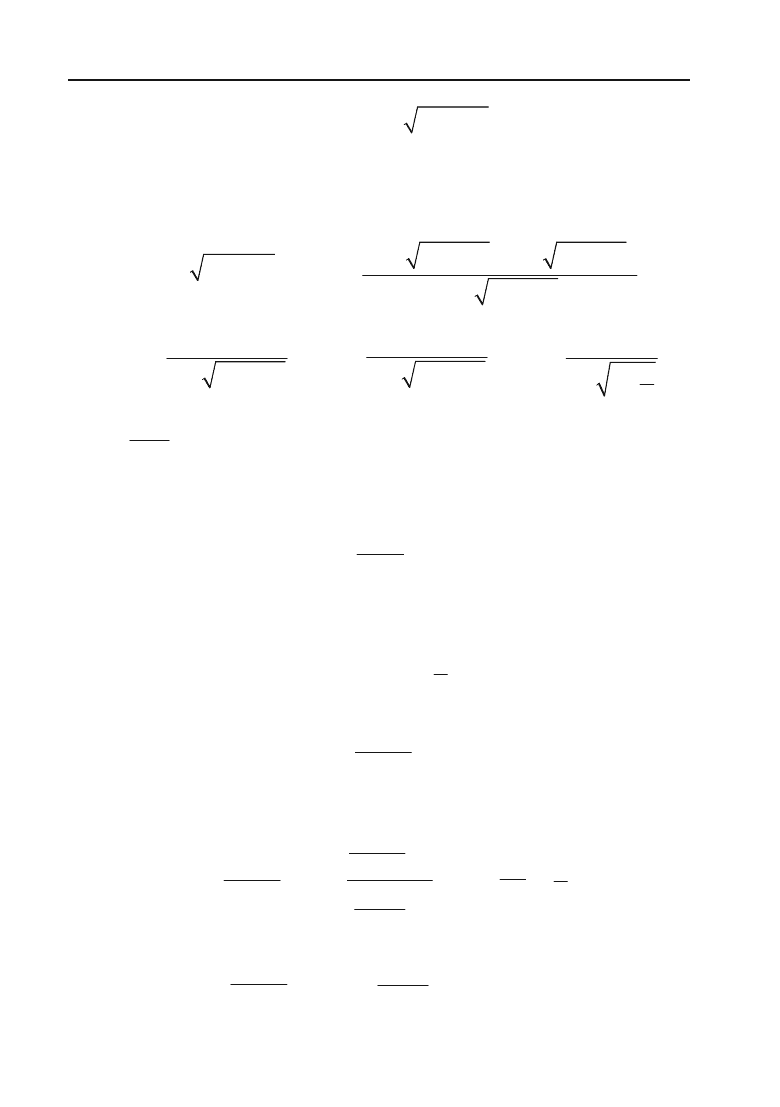
Знайти
2
lim
xo
2
14
2
4
x
x
§·
¨¸
©¹
.
Розв’язок.
Аналізуючи умову задачі, бачимо, що при вказаній
поведінці аргументу функція представляє різницю двох додатних
нескінченно великих величин (випадок
{; }ff
}). Після цього пере+
творимо задану функцію до вигляду дробу, чисельник і знаменник
якого одночасно прямує до нуля або нескінченності. Тим самим ви+
падок знаходження границі функції
{; }ff
зводиться до випадку
0
0
½
®¾
¯¿
або
f
½
®¾
f
¯¿
. Виконаємо віднімання дробів і одержаний дріб ско+
ротимо на (
х –
2):
2
lim
xo
2
14
2
4
x
x
§·
¨¸
©¹
=
2
lim
xo
24
(2)(2)
x
xx
=
2
lim
xo
2
(
2
)(
2
)
x
xx
=
=
2
lim
xo
1
2
x
=
1
4
.
218
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Приклад 3.63.
Знайти
lim
xof
2
5xx x
.
Розв’язок.
Якщо розглядати задану функцію як дробову зі знамен+
ником, рівним одиниці, та позбавившись від ірраціональності в чисель+
нику, а потім розділивши чисельник і знаменник дробу на
х
, маємо:
lim
xof
2
5
x
xx
=
lim
xof
22
2
(
5
)(
5
)
5
x
xxxxx
xx x
=
=
lim
xof
22
2
5
5
xx x
xx x
=
lim
xof
2
5
5
x
x
xx
=
lim
xof
5
5
11
x
=
=
5
11
= –
2,5
.
ІV.
Перша визначна границя
0
lim
xo
sin x
x
= 1.
Встановлюємо, що задана функція не визначена в граничній точці
і при заданій зміні аргументу вона представляє відношення двох
нескінченно малих величин (випадок
0
0
½
®¾
¯¿
).
Приклад 3.64.
Знайти
0
lim
xo
sin
sin
kx
lx
.
Розв’язок.
0
lim
xo
sin
sin
kx
lx
=
0
lim
xo
sin
sin
kx
kx
kx
lx
lx
lx
=
0
lim
xo
kx
lx
=
k
l
.
0
lim
xo
sinkx
kx
та
0
lim
xo
sinlx
lx
рівні одиниці.
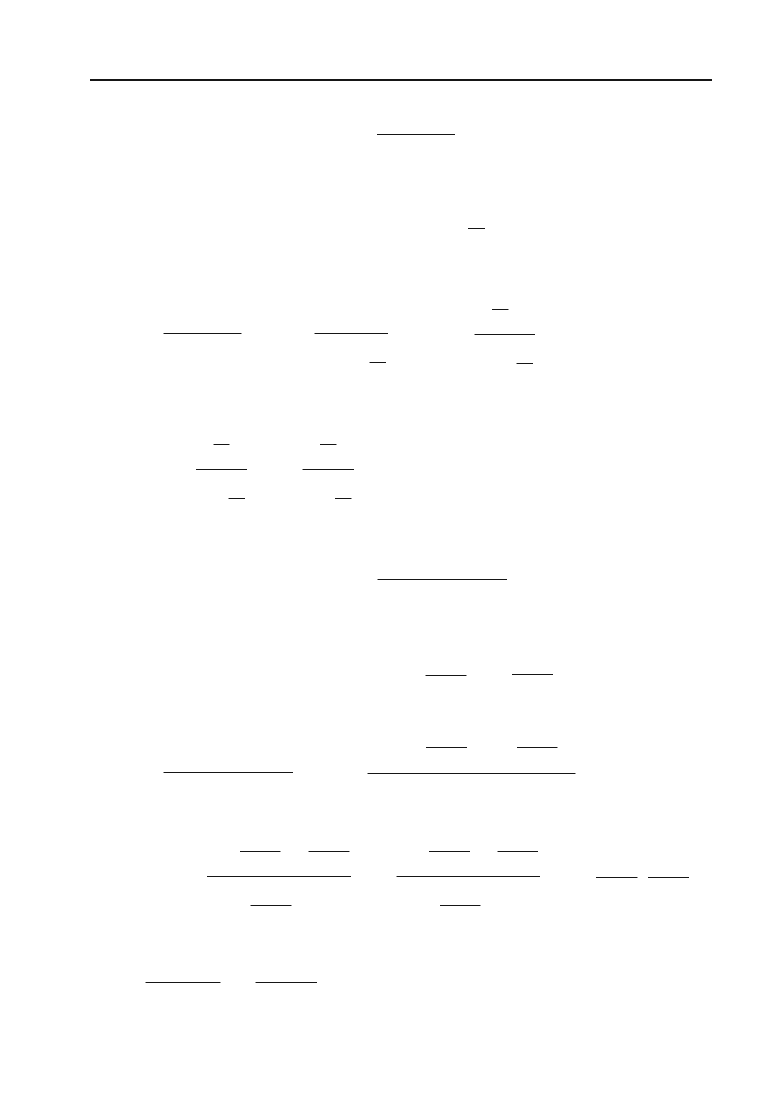
219
Розділ III. Вступ до математичного аналізу
Приклад 3.65.
Знайти
0
lim
xo
2
1cos
x
x
.
Розв’язок.
Перетворимо тригонометричну функцію
2
1cos 2sin
2
x
x
.
0
lim
xo
2
1cos
x
x
=
0
lim
xo
2
2
2sin
2
x
x
=
0
2lim
xo
2
2
4
sin
2
x
x
=
=
0
2lim
xo
2
sin
2
x
x
0
lim
xo
2
sin
2
x
x
= 2
11 = 2.
Приклад 3.66.
Знайти
0
lim
xo
2
cos coskx lx
x
.
Розв’язок.
Перетворимо формулу
cos
kx –
cos
lx = –
2sin
2
kl
x
sin
2
kl
x
.
0
lim
x o
2
cos coskx lx
x
=
0
lim
x o
2sin sin
22
kl kl
x
x
x
x
=
=
0
2lim
xo
sin
22
2
kl kl
x
kl
x
0
lim
x o
sin
22
2
kl kl
x
kl
x
=
2
22
klkl
=
=
22
2
kl
=
22
2
lk
.
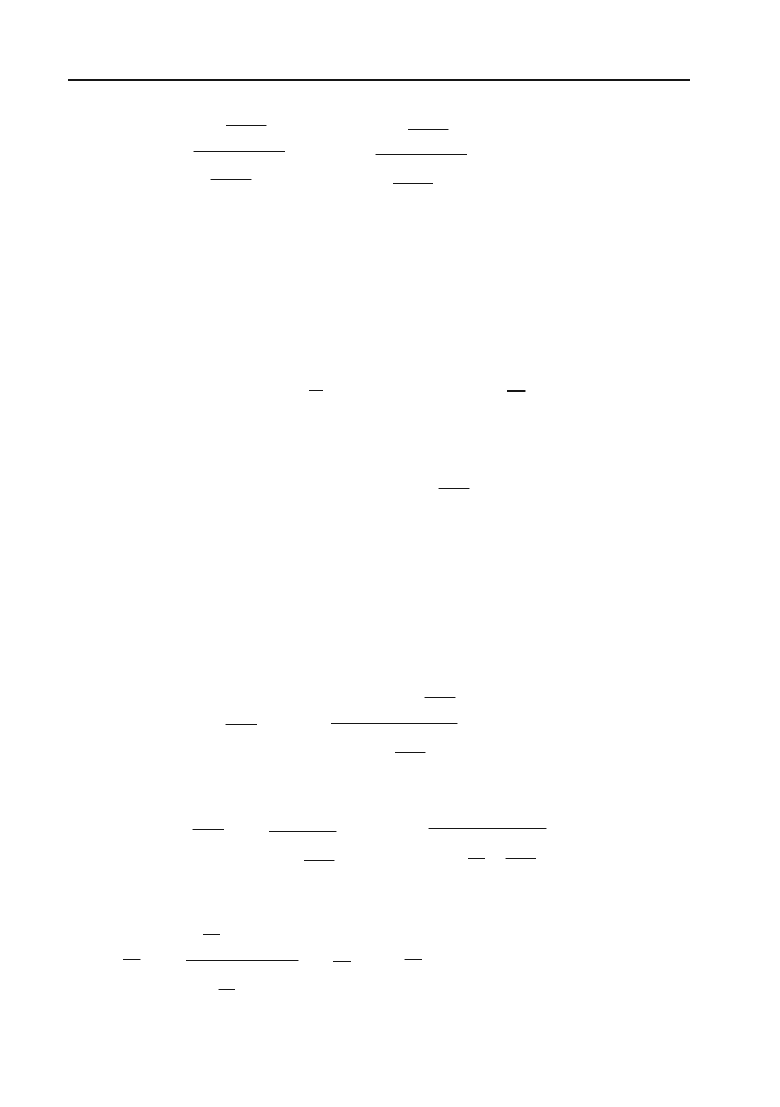
220
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
0
lim
x o
sin
2
2
kl
x
kl
x
та
0
lim
xo
sin
2
2
kl
x
kl
x
рівні одиниці.
V.
Випадок, коли при
x
of
або
x
ao
функція
f
(
x
) представ+
ляє добуток нескінченно малої величини на нескінченно велику (ви+
падок
{0 }f
). Цей випадок знаходження границі функції зводиться
шляхом перетворення функції до одного із двох розглянутих відно+
шень (тобто до випадку
0
0
½
®¾
¯¿
або до випадку
f
½
®¾
f
¯¿
).
Приклад 3.67.
Знайти
1
lim
xo
(1 ) tg
2
x
x
S
.
Розв’язок.
Встановивши, що при вказаній зміні аргументу функ+
ція представляє добуток нескінченно малої величини на нескінчен+
но велику величину (невизначеність
{0 }f
), перетворимо її до виду
дробу, чисельник і знаменник якого одночасно прямує до нуля або
нескінченості.
1
lim
xo
(1 ) tg
2
x
x
S
=
1
lim
xo
(1 ) sin
2
cos
2
x
x
x
S
S
=
=
1
lim
xo
sin
2
x
S
1
lim
xo
(1 )
cos
2
x
x
S
=
1
1lim
xo
(1 )
sin( )
22
x
x
SS
=
=
2
S
1
lim
xo
(1 )
2
sin (1 )
2
x
x
S
S
=
2
1
S
=
2
S
.
