Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


231
Розділ III. Вступ до математичного аналізу
§3.6. Економічні задачі, пов’язані з послідовністю та її
границею (елементи математики фінансів)
Розглянемо загальноприйняті в ринковій економіці алгоритми
нарахування відсотку в залежності від терміну позички, типу
відсотків, схеми їхнього нарахування.
3.6.1. Поняття відсотка
Відсотком (процентом) від числа а називається сота частина цьо+
го числа. Запис 1% означає 0,01.
Наприклад: 7% = 0,07; 7% числа
а
становить 0,07
а
.
Для того, щоб знайти відсотковий вираз заданого числа (цілого
чи десяткового дробу), достатньо помножити це число на 100.
Приклад 3.123.
Відсотковий вираз числа 5 (відносно одиниці) є
500%; числа 0,675 є 67,5%.
Для того, щоб знайти число за його відсотковим виразом достат+
ньо поділити відсотковий вираз на 100.
Приклад 3.124.
24,5% = 0,245; 3,5% = 0,035.
3.6.2. Три основні задачі на відсотки
1 задача.
Знайти певний відсоток заданого числа. Задане число
а
ділиться на 100 і множиться на відповідне число відсотків.
Приклад 3.125.
Певний добовий видобуток вугілля на шахті має
становити 3000 т. Шахта виконала добовий план на 120%. Скільки
тон вугілля дала вона за добу?
3000 120
3600 ( )
100
т
.
2 задача.
Знайти число за відомим значенням його відсотка. За+
дане значення відсотка (відому частину числа) шуканого числа діли+
мо на число, що виражає цей відсоток, а результат помножуємо на
100.
Приклад 3.126.
Маса цукру становить 12,5% маси перероблених
буряків. Скільки потрібно буряків для одержання 5000 т цукру?

232
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
3.6.3. Формула простого відсотка
Відношення даного відсотка певного числа (скажемо, грошової
суми) до самого цього числа називається відсотковою ставкою і по+
значається
р
.
Питомою відсотковою сумою (нормою відсотка) називається
відношення:
100
p
i
.
Якщо певний відсоток деякої грошової суми додається до цієї
суми, то говорять про накопичення грошей.
Якщо відсоток не нараховується на перший відсоток, що додаєть+
ся до початкового числа, говорять про простий відсоток.
Позначимо через
А
грош. од
.
первісну суму. Якщо відсоткова
ставка дорівнює
р
, а питома відсоткова ставка дорівнює
і
, то після
першого року:
А
1
= А +
100
Ap
= А + Аі = А
(1
+і
);
після другого року:
А
2
= А + Аі + Аі = А
(1+2
і
);
+ + + + + + + + + + +
А
n
= А
(1 +
ni
)
.
5000 100
40000 ( )
12,5
т
.
3 задача.
Знайти вираз даного числа у відсотках іншого (так зва+
не відсоткове відношення двох чисел). Ділимо одне число на інше
(знаходимо їх відношення) і результат помножуємо на 100.
Приклад 3.127.
Плановий видобуток нафти має становити 160
млн т фактичний видобуток досяг 164 млн т. На скільки відсотків
був виконаний план видобутку нафти?
164
100 102,5%
160
.

233
Розділ III. Вступ до математичного аналізу
3.6.4. Формула складного відсотка
Нехай на початкове число
А
нараховується складний відсоток за
певною нормою протягом
n
років. Тоді дістаємо таку послідовність
сум:
після 1+го року:
А
1
= А + іА = А
(1 +
і
);
після 2+го року:
А
2
= А
1
+ іА
1
= А
(1 +
і
)
2
;
+ + + + + + + + + + + +
після
n
+го року:
А
n
= А
n–1
+
іА
n–1
= А
(1 +
і
)
n
.
Остаточна (кінцева) сума
А
n
при нарахуванні складного відсотка
протягом
n
років становить
А
n
= А
(1 +
і
)
n
.
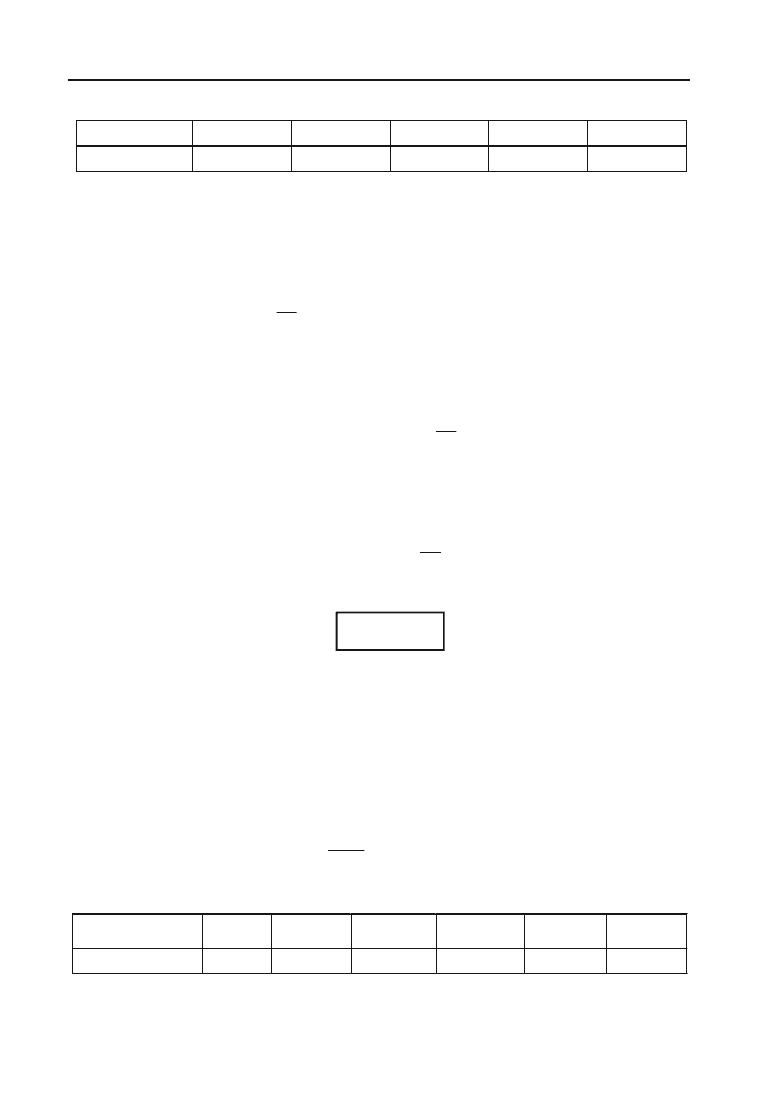
Основна формула складного відсотка
Якщо складний відсоток нараховується протягом
n
років, вико+
нується така залежність:
Вираз 1
+ і
= r
називається
коефіцієнтом складного відсотка
.
Приклад 3.129.
Нехай певний вклад
А =
250000 грош. од
.
Вкла+
даємо на 4 роки під складні відсотки за ставкою 100% річних. Знай+
ти нарощуване значення вкладу за роками.
Розв’язок
. Позначимо
А
k
– нарощуване значення вкладу на+
прикінці
k
+го року. Оскільки
А
= 250000 грош. од.
100
100
i
=
1 то за
формулою:
А
k
= А
(1
+ і
)
k
маємо:
А
k
=
250
10
3
(1 + 1)
k
=
250
10
3
2
k
,
k =
1,4
.
Отже,
Приклад 3.128.
Якщо
А =
5000, а відсоткова ставка
р =
4, то
накопичена протягом трьох років сума буде така:
А
3
= 5000(1 + 3
0,04) = 5000
1,12 = 5600.
Якщо відсоток початкового числа додається до цього числа, а далі
відсоток нараховується на утворену суму, тобто на більше число, то
говорять про складні відсотки.
А
n
= А
(1
+ ni
).
А
n
= А
(1
+ i
)
n
.
234
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
3.6.5. Формула, коли відсотки нараховуються неперервно
Нехай відсотки нараховуються рівномірно
т
разів протягом року,
кожний раз за нормою
i
m
на новий залишок вкладу (сума вважається
стабільною протягом усього розглядуваного періоду), тоді загальний
член цієї послідовності буде мати вигляд:
А
n
= А
(1 +
i
m
)
mn
.
Нехай відсотки тепер нараховується неперервно, тобто
m of
,
тоді отримаємо:
lim
mof
А
n
=
lim
mof
А
(1
+
i
m
)
mn
=
Ае
іn
.
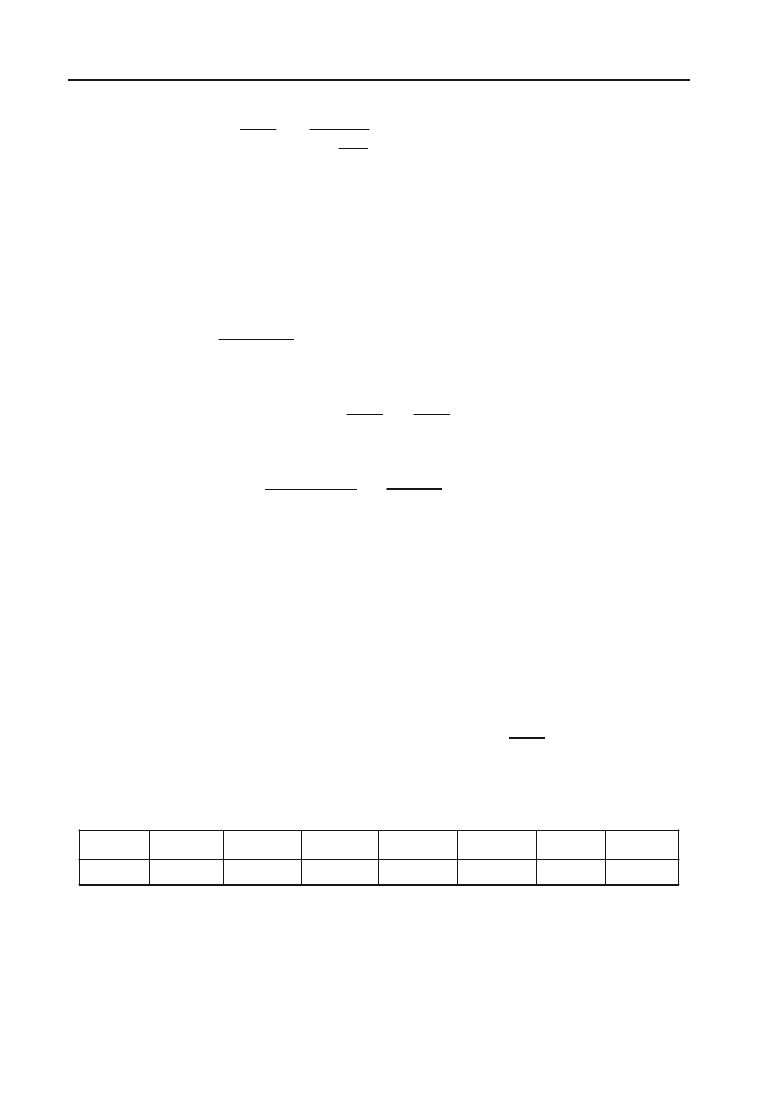
Отже,
Цю формулу можна використати для будь+яких розрахунків,
пов’язаних зі складними відсотками.
Приклад 3.130.
Сума 2000 грош. од. покладена в банк за схемою
неперервного нарахування відсотків за ставкою 10% за рік. Знайти
нарощену на протязі року суму
А
n
при
n
= 1, 2, 3, 5 I 10.
Розв’язок.
А
n
= Ае
іn
;
і =
10
100
=
0,1;
А
n
=
2000
е
0,1n
.
Результати обчислень зведемо до таблиці:
Складемо таблицю:
k, років 0 1 2 3 4
А
k
250
10
3
5
10
5
10
6
2
10
6
4
10
6
n, років 0 1 2 3 5 10
А
n
, грош. од. 2000 2210,34 2442,81 2699,72 3297,44 5436,54
А
n
= Ае
іn
.

235
Розділ III. Вступ до математичного аналізу
3.6.6. Дисконтування
Наведені вище формули зв’язують змінні величина
А
,
А
n
,
i
,
n
,
де
і =
100
p
, р
— процентна ставка. Знаючи три з них, можна знайти
четверту.
Наприклад, з основної формули для нарахування складних
відсотків
А
n
= А
(1 +
100
p
)
n
, після нескладних перетворень, отримає+
мо наступні формули:
100
ln ln
ln(1 )
n
p
AA
n
;
p =
100
1
1
n
n
A
A
§·
§·
¨¸
¨¸
¨¸
©¹
¨¸
©¹
;
A = A
n
(1
+
100
p
)
–n
=
(1 )
100
n
n
A
p
.
Відмітимо, що операція знаходження первісного вкладу
А
нази+
вається дисконтуванням. Значення
А
називають також сучасним
значенням для
А
n–
. Різницею
D
між кінцевою сумою
А
n–
, та сумою
А
,
що дисконтується, називається дисконтом:
D = А
n–
– A
.
Якщо грошові кошти
А
вкладати під прості відсотки на
n
років
за питомою відсотковою ставкою
і
, то остання сума буде така:
А
n–
= А
(1
+ nі
).
Отже, дисконтовані грошові кошти становитимуть:
1
n
A
A
ni
.
У разі складних відсотків маємо:
А
n
= А
(1
+ і
)
n
, а дисконтоване
значення грошової суми:
(1 )
n
n
A
A
i
.
236
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
3.6.7. Приклади розв’язання задач
Задача 3.132.
Нехай 2 млн. грош. од.
видано в кредит на 6 місяців
під прості відсотки за ставкою 10%
за місяць. Знайти нарощуване
значення боргу наприкінці кожного місяця.
Розв’язок.
Позначимо
A
k
— нарощуване значення боргу наприкінці
k
+го місяця. Оскільки
А =
2 млн. грош. од.,
і =
10
100
=
0,1, то вихо+
дячи з формули
А
k
= А
(1 +
ki
) маємо
А
k
=
2(1 + 0,1
i
)
, k =
1,6. Опи+
саний результат представимо у вигляді таблиці:
Ми бачимо, що послідовність
А
0
= А
,
А
1
,
А
2
,
... ,
А
k
— це арифме+
тична прогресія з початковим числом
А
0
=
2 млн. грош. од. і різницю
200 тис грош. од.
Коефіцієнт
1
1 i
Q
=
100
1
1
p
називають
коефіцієнтом дисконту
.
Приклад 3.131.
Потрібно знайти сумарне значення боргу (перв+
існий борг), повна сума якого через 3 роки складе 7 млн грош. од.
Відсотки нараховуються за наступною ставкою 20% наприкінці кож+
ного року.
Розв’язок
.
А =
(1 )
n
mn
A
i
, де
n =
3,
А
3
= 7
10
6
(
грош. од.
),
т
= 4,
і =
100
p
=
20
100
=
0,2;
А =
6
12
710
(
10,2
)
=
6
710
8,916
= 785105.
K 0 1 2 3 4 5 6
A
k
2 2,2 2,4 2,6 2,8 3 3,2

237
Розділ III. Вступ до математичного аналізу
Задача 3.133.
Сума 800 тис грош. од. інвестується на 3 роки під
складні відсотки за ставкою 80% річних. Знайти нарощену суму за
цей період.
Розв’язок.
Скористаємося формулою
А
n
= А
(1
+ і
)
n
, де
n =
3,
A =
800 тис грош. од.,
p =
80%,
i =
100
p
=
80
100
=
0,8.
A
3
=
800(1 + 0,8)
3
= 800(1,8)
3
= 800
5,832 = 4665,5 (
тис грош. од.
).
Задача 3.134.
При одній і тій же відсотковій ставці за схемою
неперервного нарахування відсотків вкладник
С
через 2 роки одер+
жує 1000 грош. од., вкладник
Д
через 4 роки одержує 600 грош. од.
Знайти відсоткову ставку
р
, якщо первісний вклад вкладника
С
вдвічі
більше, ніж вклад вкладника
Д
.
Розв’язок.
Скористаємося формулою
А
n
= Ае
іn
. Тоді
А
2
= А
(С)
е
2і
;
А
4
= А
(Д)
е
4і
. Позначимо через
А
(С)
і
А
(Д)
—
початкові вклади вклад+
ників
С
і
Д
відповідно. Звідси
А
(с)
= А
2
е
–2і
;
А
(Д)
=А
4
е
–4і
.
Враховуючи,
що
А
(С)
=
2
А
(Д)
, маємо:
1000
е
–2і
=
1200
е
–4і
.
Звідси
е
2і
=
1,2;
2
і =
ln
1,2;
i =
1
2
ln 1,2 = 0,09116;
p
=
i
100%
=
9,1%.
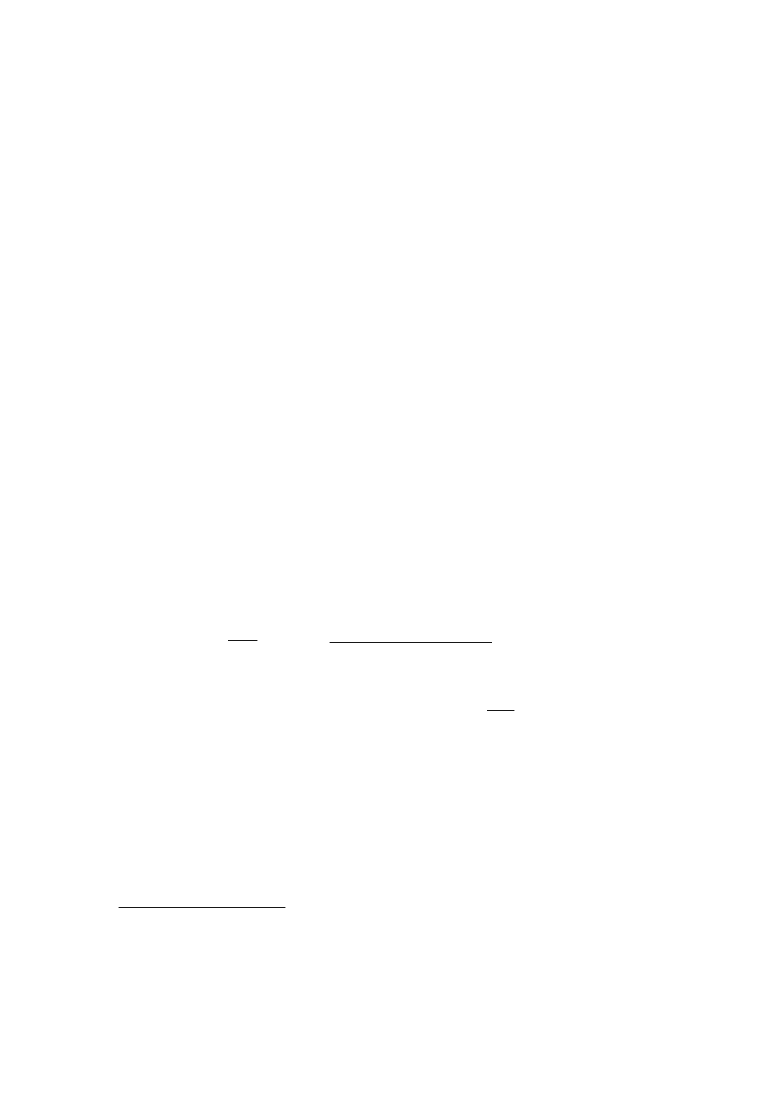
238
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Розділ ІV. Диференційне числення функції однієї
змінної
Під час вивчення економічних понять, таких, наприклад, як по+
пит, витрати виробництва, національний прибуток, часто доводить+
ся визначати швидкість зміни значень відповідних величин. Розв’я+
зуючи такі задачі, застосовують методи диференціального числення.
§4.1. Означення похідної. Залежність між неперервністю
та диференційовністю функції. Правила диференціювання.
Похідні основних елементарних функцій
4.1.1. Означення похідної
Похідною функції y = f(x) по аргументу х
називається границя
відношення її приросту
y
'
до відповідного приросту
x'
незалеж+
ної змінної, коли
0x'o
:
0
lim
x'o
y
x
'
'
=
0
lim
x'o
()()
f
xx
f
x
x
'
'
=
()
f
x
c
.
Похідна позначається
()
f
x
c
або
y
c
, або
dy
dx
. Операція знаход+
ження похідної
()
f
x
c
заданої функції
f
(
x
) називається
диференці,
юванням цієї функції
.
Функція називається
диференційовною в деякій точці х
0
, якщо
в цій точці вона має визначену похідну
0
()
f
x
c
, тобто якщо
0
lim
x'o
00
()()
f
xx
f
x
x
'
'
=
0
()
f
x
c
існує і має одне й теж значення,
якщо
0x'o
будь+яким способом. При цьому функція буде і непе+
рервною в цій точці.
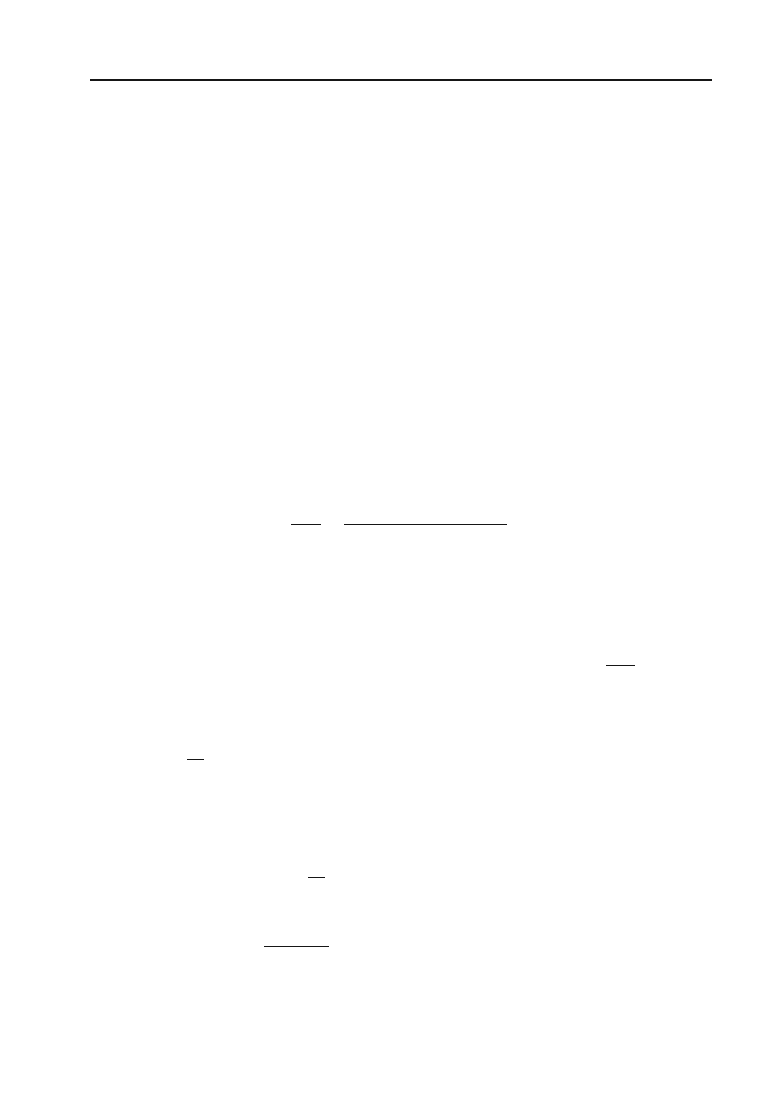
239
Розділ IV. Диференційне числення функції однієї змінної
Неперервність функції є необхідною (але недостатньою) умовою
диференційовності функції. Функція, неперервна в деякій точці
х
0
,
може бути і недиференційовною в цій точці.
Для безпосереднього знаходження похідної
y
c
від функції
у
=
f
(
x
)
служить наступне правило:
І. Надаємо аргументу
х
довільний приріст
x'
і, підставляючи в
заданий вираз функції замість
х
нарощене значення
xx'
, знахо+
димо нарощене значення функції
()
y
yfx x' '
.
ІІ. Віднімаючи із нарощеного значення функції її початкове зна+
чення, знаходимо приріст функції
()()
y
fx x fx' '
.
ІІІ Ділимо приріст функції на приріст аргументу, тобто складає+
мо відношення
()()
yf
xx
f
x
xx
''
''
.
ІV. Знаходимо границю цього відношення, якщо
0x'o
. Ця
границя і дає шукану похідну
y
c
від функції
у = f
(
x
).
Приклад 4.1.
Шляхом знаходження границі
0
lim
x
'o
y
x
'
'
знайти
похідні наступних функцій:
1)
1
y
x
;2)
у
= cos 3
x.
Розв’язок.
Користуючись вказаними загальними правилами для
безпосереднього знаходження похідної, послідовно знаходимо:
1) Для функції
1
y
x
:
І)
1
yy
x
x
'
'
;
240
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
ІІ)
y
'
=
1
xx
'
–
1
x
=
()
x
x
xx
'
'
;
ІІІ)
y
x
'
'
=
()
x
xx x
'
'
;
IV)
y
c
=
0
lim
x'o
y
x
'
'
=
0
lim
x
'o
()
()
x
xx x
'
'
=
2
1
x
.
2) Для функції
у =
cos 3
x
.
І)
cos3
()
yy
xx' '
;
ІІ)
33
cos3( ) cos3 2sin(3 )sin
22
y
xx x x x x
' ' ' '
;
ІІІ)
y
x
'
'
=
33
2sin(3 )sin
22
x
xx
x
' '
'
;
IV)
y
c
=
0
lim
x'o
y
x
'
'
=
0
3
2limsin(3 )
2
x
xx
'o
'
0
lim
x
'o
3
sin
2
x
x
'
'
=
=
0
2sin3 lim
x
x
'o
33
sin
22
3
2
x
x
'
'
=
3
2sin3 3sin3
2
xx
.
4.1.2. Основні правила та формули диференціювання
Практично ж похідні функцій знаходять за основними правила+
ми та основними формулами диференціювання.
Основні правила диференціювання:
1.
()
0C
c
.
2.
() 1
x
x
c
.
3.
()
x
xx
uvw u v w
ccc c
.
