Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

221
Розділ III. Вступ до математичного аналізу
VI.
Випадок, коли при
x
of
або
x
ao
функція
f
(
x
) представ+
ляє степінь, основа якого прямує до одиниці, а показник — до не+
скінченості. В такому випадку для знаходження границі функції
використовується друга визначна границя
lim
xof
1
1
x
x
§·
¨¸
©¹
=
0
lim
D
o
1
1
D
D
=
e
.
Приклад 3.68.
Знайти
lim
x of
1
1
x
x
x
§·
¨¸
©¹
.
Розв’язок.
Тут основа степеня
1
() 1
1
x
fx
x
o
, коли
x
of
, а
показник степеня
x
of
. Має місце випадок невизначеності виду
{1 }
f
.
lim
xof
1
1
x
x
x
§·
¨¸
©¹
=
lim
xof
111
1
x
x
x
§·
¨¸
©¹
=
lim
xof
12
11
x
x
xx
§·
¨¸
©¹
=
=
lim
x
of
2
1
1
x
x
§·
¨¸
©¹
=
lim
x
of
2
1
1
2
2
1
1
x
x
x
x
§·
§·
¨¸
¨¸
¨¸
©¹
©¹
=
lim
x
of
2
1
x
x
e
=
=
2
lim
1
x
x
x
e
of
=
2
1
lim
x
x
x
x
x
e
of
=
1
2
lim
1
x
x
e
of
=
2
e
.
Приклад 3.69.
Знайти
lim
x
of
32
41
43
x
x
x
§·
¨¸
©¹
.
Розв’язок.
lim
x of
32
41
43
x
x
x
§·
¨¸
©¹
=
lim
xof
32
4331
43
x
x
x
§·
¨¸
©¹
=
lim
xof
32
43 4
4343
x
x
xx
§·
¨¸
©¹
=

222
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
3.4.6. Приклади для самостійного розв’язку
Знайти границі:
3.71.
lim
n
of
2
2
(1)
2
n
n
.
3.72.
lim
nof
32
2
100 1
100 15
nn
nn
.
3.73.
lim
nof
32
42
1000 3
0,001 100 1
nn
nn
.
3.74.
lim
n
of
3
3
21
2
nn
n
.
3.75.
lim
n
of
3
34
45
65 74
21 1
62 31
nn n
nn nn
.
3.76.
lim
nof
!
(1)!!
n
nn
.
3.77.
lim
n
of
(2)!(1)!
(3)!
nn
n
.
=
lim
x
of
4(3 2)
43
43
4
1
1
43
4
x
x
x
x
§·
§·
¨¸
¨¸
¨¸
¨¸
¨¸
¨¸
¨¸
©¹
¨¸
©¹
=
lim
x
of
12 8
1
43
()
x
x
e
=
12 8
lim
43
x
x
x
e
of
=
=
12 8
43
lim
x
x
x
x
x
e
of
=
12
4
e
=
3
e
.
Приклад 3.70.
Знайти
1
lim
xo
5
2
1
32
x
x
x
.
Розв’язок.
1
lim
xo
5
2
1
32
x
x
x
=
1
lim
xo
5
2
1
13 12
x
x
x
=
1
lim
xo
5
(1)(1)
13( 1)
x
xx
x
=
=
1
lim
xo
15
1
3( 1) 1
13( 1)
x
xx
x
=
1
lim
x
o
15
1
x
x
e
=
1
15
lim
1
x
x
x
e
o
=
15
2
e
.
223
Розділ III. Вступ до математичного аналізу
3.78.
lim
nof
(2)!(1)!
( 2)! ( 1)!
nn
nn
.
3.79.
lim
nof
123...
22
nn
n
§·
¨¸
©¹
.
3.80.
2
lim
x
o
2
2
5
3
x
x
.
3.81.
1
lim
x
o
2
3
21xx
xx
.
3.82.
2
lim
xo
32
2
32
6
x
xx
x
x
.
3.83.
1
lim
xo
2
2
257
32
xx
x
x
.
3.84.
3
lim
x
o
2
2
6
221
xx
xx
.
3.85.
1
2
lim
xo
3
2
81
651
x
x
x
.
3.86.
1
lim
x
o
3
32
2
1
xx
xxx
.
3.87.
1
lim
xo
2
13
11
x
x
§·
¨¸
©¹
.
3.88.
3
lim
x
o
12
21
x
x
.
3.89.
4
lim
xo
213
22
x
x
.
3.90.
9
lim
x
o
275
3
x
x
.
3.91.
4
lim
x
o
2
615
x
x
.
3.92.
0
lim
xo
2
13 12
x
x
x
x
.
3.93.
0
lim
xo
33
11
x
x
x
.
3.94.
lim
xof
(
2
1x
–
2
1x
).
3.95.
lim
x
orf
(
2
1xx
).
3.96.
0
lim
x
o
2
1cosx
x
.
3.97.
0
lim
xo
3
1cos
sin 2
x
x
x
.
3.98.
0
lim
x
o
1sin cos
1sin cos
xx
xx
.
3.99.
0
lim
D
o
3
tg sin
DD
D
.
3.100.
0
lim
xo
cos
()
cos
()
ax ax
x
.
224
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
3.101.
0
lim
xo
1cos8
1cos4
x
x
.
3.102.
0
lim
xo
arctg2
5
x
x
.
3.103.
0
lim
xo
3
cos cos
sin 2
xx
xx
.
3.104.
1
lim
xo
2
sin( 1)
1
x
x
.
3.105.
lim
xof
24
7
5
x
x
x
§·
¨¸
©¹
.
3.106.
lim
xof
3
34
35
x
x
x
§·
¨¸
©¹
.
3.107.
lim
x
of
5
3
32
x
x
x
§·
¨¸
©¹
.
3.108.
0
lim
xo
12
x
x
.
3.109.
lim
xof
1
25
21
x
x
x
§·
¨¸
©¹
.
3.110.
2
lim
x
o
3
2
23
x
x
x
.
3.111.
1
lim
x
o
3
1
2
x
x
x
.
3.112.
1
lim
x
o
1
32
x
x
x
.
3.113.
lim
x
of
(2
x
+ 3)(ln(
x
+ 2) – ln
x
).
3.114.
lim
x
of
(
x
– 4)(ln(2 – 3
х
) – ln(5 – 3
x
)).
3.115.
4
lim
x
S
o
4
3
4
sin
()
x
x
S
S
.
3.116.
0
lim
x
o
1 sin 1 sin
tg
xx
x
.
3.117.
0
lim
x
o
1cos3
sin2
x
xx
.
3.118.
2
lim
x
o
2
2
4
35
x
x
x
.

225
Розділ III. Вступ до математичного аналізу
§3.5. Неперервність функції. Властивості неперервних
функцій. Розриви функцій.
Функція
f
(
x
)
називається
неперервною в точці х = а
, якщо:
1) вона визначена в цій точці;
2) існує
lim ( )
xa
fx
o
;
3) ця границя дорівнює значенню функції в точці
х = а
, тобто
lim ( ) ( )
xa
f
xfa
o
.
Якщо хоч би одна із цих умов не виконується, то функція нази+
вається
розривною в точці х = а
, а саме точка
х = а
називається
точкою розриву
.
Функція
y = f
(
x
) називається
перервною в точці х = х
0
, якщо в
цій точці нескінченно малому приросту аргументу
х – х
0
=
x'
, відпо+
відає нескінченно малий приріст функції
у – у
0
=
y
'
, тобто якщо
0
lim
xx
y
o
'
=
0
00
lim( ( ) ( ))
xx
f
xx fx
o
=
0.
Функція
у = f
(
x
) неперервна на проміжку (
а
,
b
), якщо вона непе+
рервна в кожній точці цього проміжку.
Функція
у = f
(
x
) називається
неперервною в точці х
0
справа
(зліва)
, якщо
0
0
lim
xxo
f
(
x
)
=
f
(
x
0
)
(
0
0
lim
xxo
f
(
x
)
=
f
(
x
0
)).
Функція
у = f
(
x
) неперервна на відрізку [
a, b
], якщо вона непе+
рервна на проміжку (
а
,
b
) і неперервна в точці
х = а
справа і в точці
x = b
зліва.
Усі елементарні функції неперервні на інтервалах визначеності.
Функція
у = f
(
x
), яка не є неперервною в точці
х
0
,
називається
розривною в цій точці
.
Точка
х
0
називається
точною розриву першого роду функції у = f
(
x
),
якщо існують скінчені границі
0
0
lim
xxo
f
(
x
),
0
0
lim
xxo
f
(
x
) і при цьому,
якщо виконується хоча б одна з трьох умов:

226
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
3.5.1. Розв’язання прикладів
Приклад 3.119.
Знайти точки розриву функції
2
1
4
y
x
.
Розв’язок.
Функція
2
1
4
y
x
визначена при всіх значеннях
х
,
крім
х =
r
2. Ця функція елементарна, через це вона неперервна на
0
0
00
0
0
0
0
00
lim ( ) ( )
lim ( ) ( )
lim ( ) lim ( )
xx
xx
xx xx
fx fx
fx fx
f
xfx
o
o
o o
½
z
°
°
z
¾
°
z
°
¿
неусувний розрив І+го роду
4)
0
0
lim
xxo
f
(
x
)
=
0
0
lim
xxo
f
(
x
)
z
f
(
x
0
)
—
усувний розрив І+го роду.
Точка
х
0
називається
точкою розриву другого роду функції у = f
(
x
),
якщо одна із границь
0
0
lim
xxo
f
(
x
),
0
0
lim
xxo
f
(
x
)
не існує або нескінченна.
Стрибком функції в точці розриву х = х
0
називається різниця її
односторонніх границь
0
0
lim
xxo
f
(
x
)
–
0
0
lim
xxo
f
(
x
), якщо вони різні.
При знаходженні точок розриву функції можна керуватися на+
ступними положеннями:
1) елементарна функція може мати розрив тільки в окремих точках,
але не може бути розривною у всіх точках якого+небудь інтервалу;
2) елементарна функція може мати розрив лише в тій точці де
вона не визначена, при умові, якщо вона буде визначена хоча би з
однієї сторони від цієї точки в як завгодно близьких до неї точках;
3) неелементарна функція може мати розриви як в точках, де вона
невизначена, так і в таких, де вона визначена, зокрема, якщо функ+
ція задана кількома різними аналітичними виразами (формулами)
для різних інтервалів зміни аргументу, то вона може мати розриви в
тих точках, де змінюється її аналітичний вираз.
227
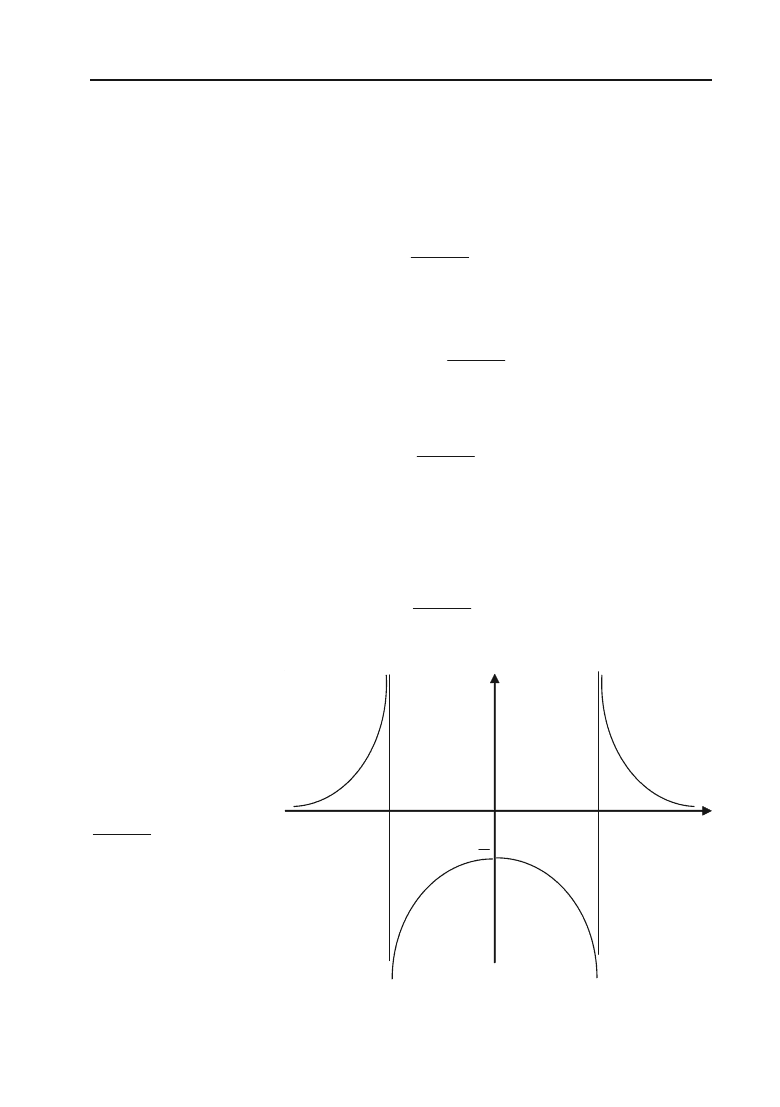
Розділ III. Вступ до математичного аналізу
всій області свого визначення:
f
<
х <
–2, –2 <
x
< 2, 2 <
x <
f
.
Вона не визначена в точках
х
1
=
2
і
х
2
=
–2, але визначена поблизу
цих точок. Задана функція в точках
х
1
і
х
2
має розриви. Знайдемо
односторонні границі заданої функції при прямуванні аргументу
х
до точок розриву зліва і справа.
а)
20
lim
x
y
o
=
20
lim
xo
2
1
4x
=
f
,
так як при
20
x
o
величина
х
2
– 4
є додатною нескінченно ма+
лою величиною, а обернена її величина
2
1
4x
є додатною нескінчен+
но великою;
20
lim
x
y
o
=
20
lim
x
o
2
1
4x
=
f
,
так як при
20
x
o
величина
х
2
–
4
є від’ємною нескінченно
малою, а обернена її величина є від’ємною нескінченно великою.
Отже, в точці
х = –
2
функція має нескінчений розрив.
б)
20
lim
x
y
o
=
20
lim
x
o
2
1
4x
=
f
,
так як при
20
x
o
величина
х
2
– 4
є від’ємною
нескінченно малою
величиною, а обер+
нена її величина
2
1
4x
є від’ємною
нескінченно вели+
кою;
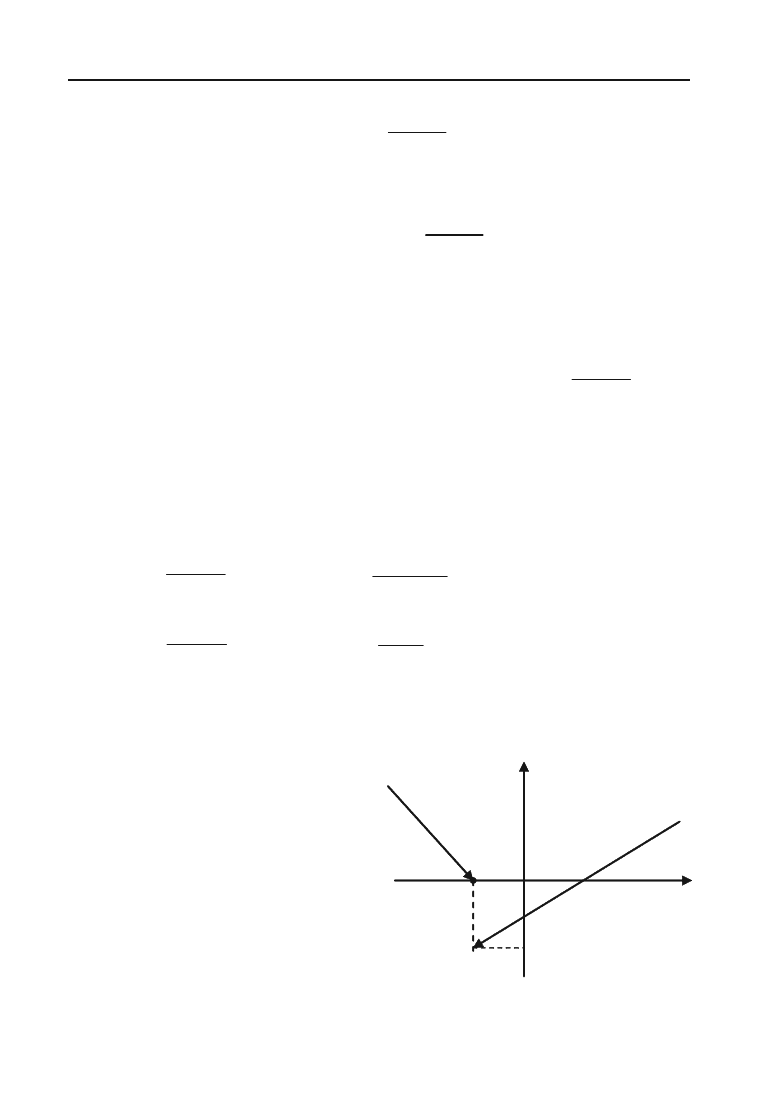
–2 0 2 Х
1
4
Y
Рис. 3.34.
228
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
20
lim
x
y
o
=
20
lim
x
o
2
1
4x
=
f
,
так як при
20
x
o
величина
х
2
–
4
є додатною нескінченно ма+
лою величиною, а обернена її величина
2
1
4x
є додатною нескінчен+
но великою.
Отже, в точці
х =
2
функція має нескінчений розрив. Див. рис.
3.34.
Приклад 3.120.
Знайти точки розриву функції
|1|
1
1
x
y
x
x
і
стрибок функції в точці розриву.
Розв’язок.
Задана функція визначена і неперервна на всій числовій
осі крім точки
х =
–1. Із цього слідує, що в точці
х =
–1 функція має
розрив.
Дослідимо цю точку розриву
10
lim
x
o
|1|
(1)
1
x
x
x
=
10
lim
xo
(
(1)
1
1
x
x
x
)
=
10
lim
x
o
(–
х
– 1)
= 0
.
10
lim
x
o
(
|1|
1
1
x
x
x
)
=
10
lim
x
o
(
1
1
1
x
x
x
)
=
10
lim
x
o
(
х –
1) = –2.
Отже, односторонні границі функції в точці
х
= –1 існують, але
не рівні між собою. В цій точці задана функція має розрив першого
роду. Стрибок функції дорівнює
10
lim
x
y
o
–
10
lim
x
y
o
=
–2 – 0 = –2.
Графік функції складається із
двох напівпрямих:
1, 1
1, 1
xприx
y
xприx
®
!
¯
.
Її графік зображено на рис.
3.35.
–1 0 1 Х
–2
Y
y = x – 1
y
= – x – 1
Рис. 3.35.

229
Розділ III. Вступ до математичного аналізу
Приклад 3.121.
Для заданої функції
2, 0 1,
() 4 2, 1 2,5,
27, 2,5 .
xпри х
fx хпри x
xпри x
dd
°
®
°
df
¯
знайти точки розриву та стрибки функції в точках розриву, побуду+
вати графік.
Розв’язок.
Неелементарна функція
f
(
x
) визначена для всіх зна+
чень
х
t
0. Вона може мати розрив в точках
х =
1
і
х =
2,5,
де
змінюється її аналітичний вираз. У всіх інших точках своєї області
визначення
f
(
x
) неперервна, так як кожна із формул, якими вона
задана, визначає собою елементарну функцію, неперервну в своєму
інтервалі зміни аргументу
х
.
Дослідимо точки
х =
1
і
х =
2,5:
а)
10
lim
xo
f
(
x
)
=
10
lim
xo
2
x
=
2;
10
lim
xo
f
(
x
)
=
10
lim
x
o
(4 – 2
x
)
=
2.
Згідно умови значення функції
f
(
x
) в точці
х
= 1
визначається
першою формулою
f
(1)
=
21
=
2. Отже, в точці
х
= 1 виконуються
всі умови неперервності: функція визначена в околі точки
х
= 1
і
10
lim
xo
f
(
x
)
=
10
lim
x
o
f
(
x
)
=
1, через це в точці
х
= 1 функція
f
(
x
) неперер+
вна.
б)
2,5 0
lim
x
o
f
(
x
)
=
2,5 0
lim
x
o
(4 – 2
x
) = –1;
2,5 0
lim
x
o
f
(
x
)
=
2,5 0
lim
x
o
(2
x
– 7) = –2
.
Тут границі зліва та справа існують і скінчені, але не однакові,
тобто не виконується умова неперервності. Через це в точці
х =
2,5
функція має розрив І+го роду. Стрибок функції в точці розриву:
2,5 0
lim
x
o
f
(
x
)
–
2,5 0
lim
x
o
f
(
x
)
=
–2 – (–1) = –1.
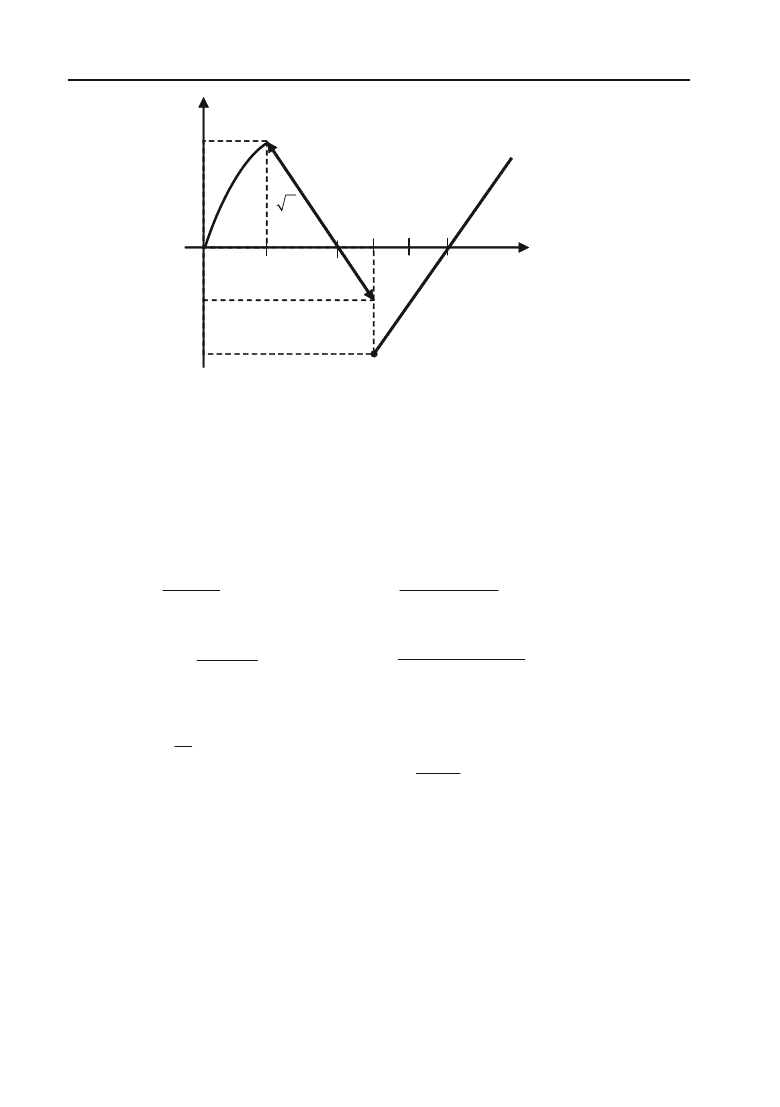
Див. рис. 3.36.
230
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
3.5.2. Приклади для самостійного розв’язку
3.122.
Задана функція. Знайти її точки розриву, якщо вони існу+
ють, і стрибок функції в кожній точці розриву:
а)
2
9
x
y
x
;б)
2
4
21
y
xx
;
в)
2
|2|
x
yx
x
;г)
32
1
34
y
xxx
;
д)
1
1x
y
e
;ж)
, 1,
2
, 1.
1
xприх
y
при х
х
d
°
®
!
°
¯
Y
2
0
–1
–2
1 2 2,5 3 3,5 X
2yx
y = 4 – 2x
y = 2x – 7
Рис. 3.36.
