Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


241
Розділ IV. Диференційне числення функції однієї змінної
4.
()
x
Cu C u
cc
.
5.
()
x
x
uv u v uv
cc c
.
6.
2
x
x
uv uv
u
vv
c
cc
§·
¨¸
©¹
,
(Тут
С
— стала величина,
u
,
v
— функції аргументу
х
, що мають
похідні).
7. Нехай
y
=
f
(
M
(
x
)) — складна функція, тобто
y
=
f
(
u
), а
u
=
M
(
x
).
Якщо для відповідних один одному значень
х
і
u
існують похідні
()
u
f
u
c
i
()
x
ux
M
cc
, то існує похідна від
у
по
х
, причому
() ()
xu x
y
fuu x
cc c
.
Користуючись цим співвідношенням, таблицю формул диферен+
ціювання можна подати так:
8.
a
y
u
;
2
x
x
a
y
u
u
cc
(
a
— стала величина).
9. а)
y
=
u
n
;
1n
x
x
y
nu u
cc
.
б)
y
u
;
1
2
x
x
y
u
u
cc
.
10.
y
= sin
u
;
cos
x
x
y
uu
cc
.
11.
y
= cos
u
;
sin
x
x
y
uu
cc
.
12.
y
= tg
u
;
2
1
cos
x
x
y
u
u
cc
.
13.
y
= ctg
u
;
2
1
sin
x
x
y
u
u
cc
.
14.
y
= arcsin
u
;
2
1
1
x
x
y
u
u
cc
.
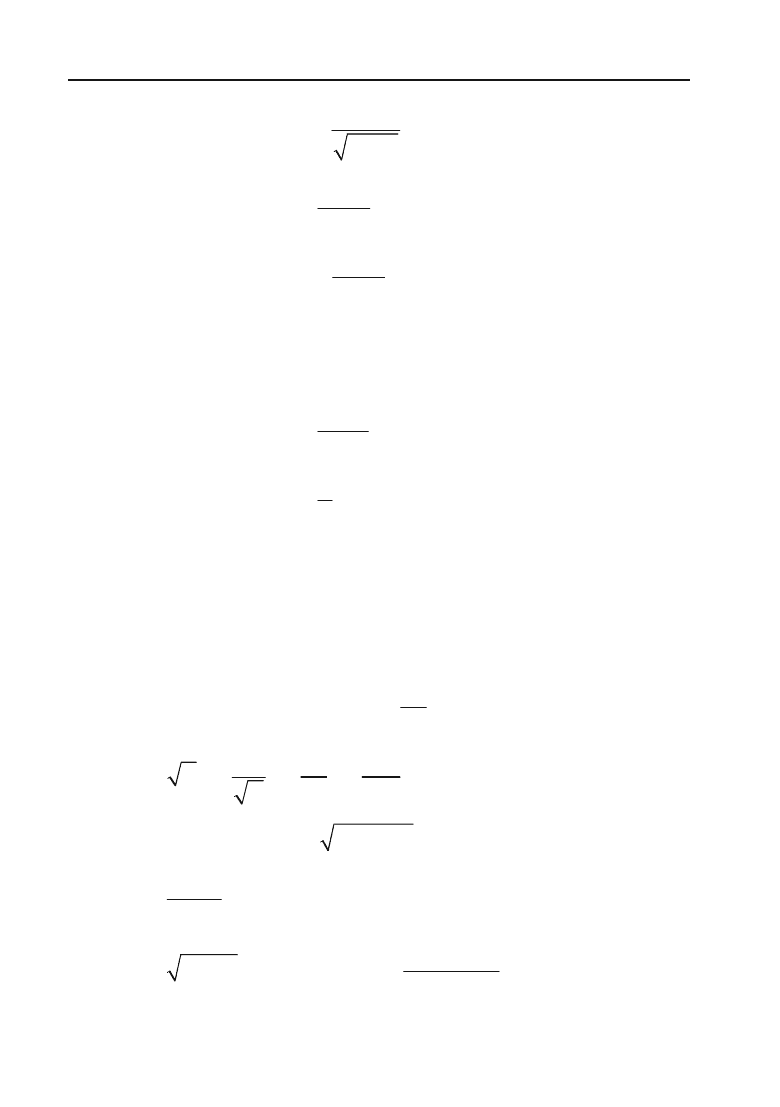
242
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
15.
y
= arccos
u
;
2
1
1
x
x
y
u
u
cc
.
16.
y
= arctg
u
;
2
1
1
x
x
y
u
u
cc
.
17.
y
= arcctg
u
;
2
1
1
x
x
y
u
u
cc
.
18. a)
y
=
a
u
;
ln
u
x
x
y
aau
cc
;
б)
y
=
e
u
;
u
x
x
y
eu
cc
.
19. a)
y
= log
a
u
;
1
ln
x
x
y
u
ua
cc
;
б)
y
= ln
u
;
1
x
x
y
u
u
cc
.
20. a)
y
=
u
v
; де
()
ux
M
,
()
vx
\
,
1
ln
vv
x
xx
y
vu u u uv
ccc
.
Приклад 4.2.
Знайти похідні; користуючись формулами диферен+
ціювання:
1)
y = x
2
–
5
x +
4; 2)
2
8
y
x
;
3)
y =
x
+
3
5
x
–
2
1
x
+
3
1
3x
;
4)
y =
(3
x
2
+ 5
ax –
2
a
2
)
22
3ax
;
5)
y =
2
2
1
x
x
;6)
y =
(5
x
3
+
4
x
2
+
8)
4
;
7)
y =
3
4
2
x
;8)
y =
23
3
(3 5)x
;
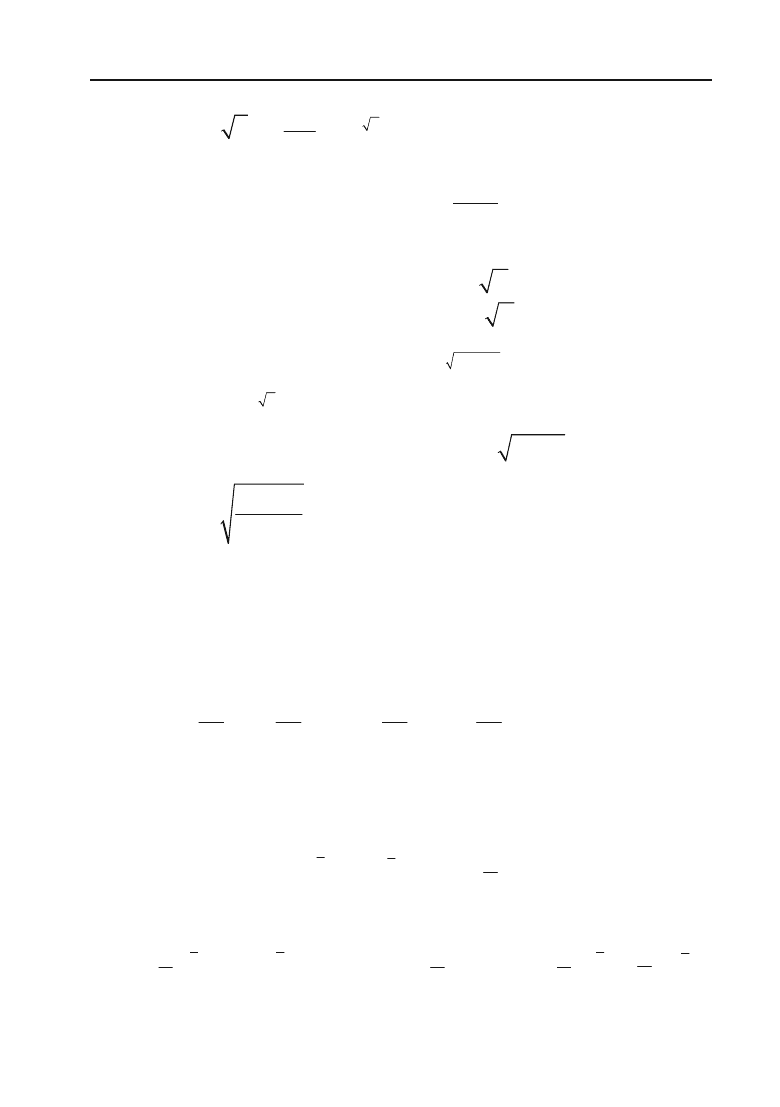
243
Розділ IV. Диференційне числення функції однієї змінної
9)
f
(
x
)
=
3
x
+
5
1
2
x
+
6
x
,
обчислити
(1)f
c
;
10)
y =
sin 2
x
2
; 11)
y =
tg
1 x
x
;
12)
y =
3sin
2
x
; 13)
y =
sin
3
5
x
cos
5
3
x
;
14)
y =
arcsin2
x
; 15)
y =
arctg
x
;
16)
y =
arccos
2
3
x
; 17)
y =
arctg
4
3
x
;
18)
y =
2
sin 3
4
x
; 19)
y =
2
3xx
e
;
20)
y =
3
arcsin
x
e
; 21)
y =
lncos3
x
;
22)
y
= ln
5
ctg4
x
; 23)
y =
2
ln
(
1
)
x
x
;
24)
y =
4
1tg
ln
1tg
M
M
; 25)
y = x
x
.
Розв’язок.
1)
22
(9 ; 4; 1)
(3)
(54)()(5)4 251025
за формулами а
за формулою
yx x x x x x
ccccc
.
1)
2
24 4 3
(8; 9 )
88 8 16
() 2
за формулами а
yxx
xx x x
c
§·
cc
¨¸
©¹
.
2) Ввівши дробові та від’ємні показники, перетворимо задану
функцію:
y =
1
2
x
+
1
3
5x
–
2
x
+
3
1
3
x
.
Застосовуючи формули (9
а
, 4, 2), одержуємо:
y
c
=
1
1
2
1
2
x
+
1
1
3
5x
–
(–2)
x
–2–1
+
31
1
(3)
3
x
=
1
2
1
2
x
+
5
3
4
3
x
+
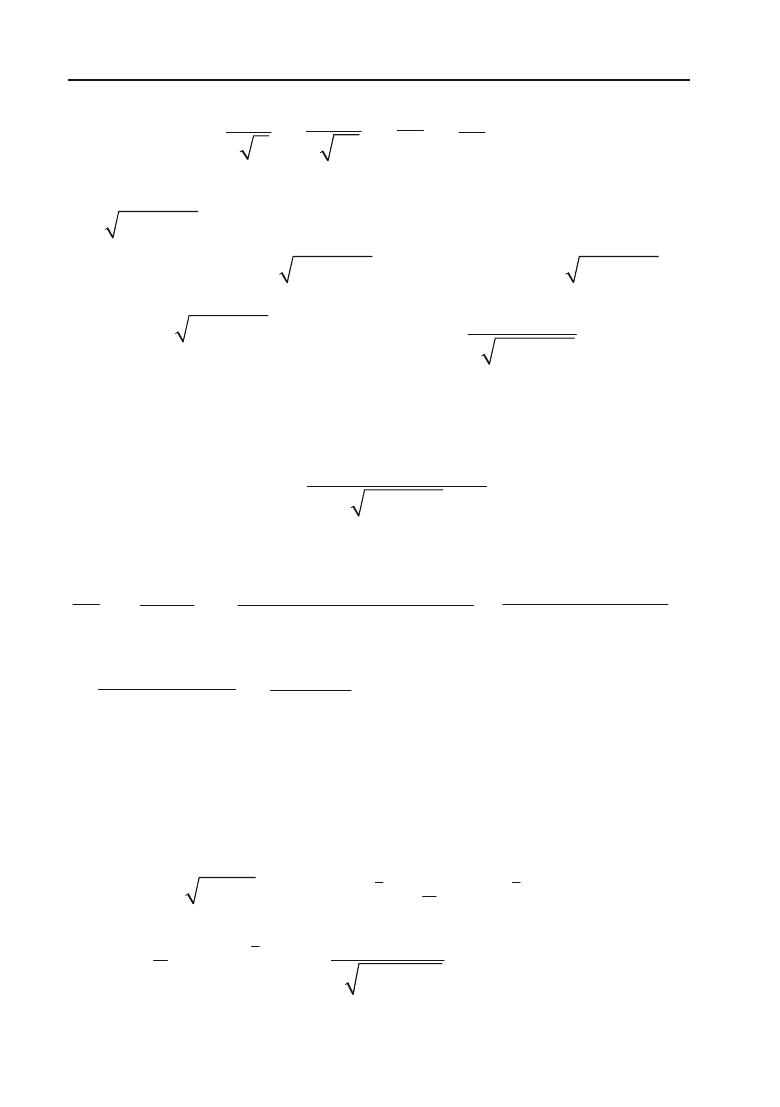
244
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
+
2
x
–3
– x
–4
=
1
2 x
–
4
3
5
3
x
+
3
2
x
–
4
1
x
.
3) За формулою (5) маємо при
u =
3
x
2
+
5
ax –
2
a
2
,
22
3va x
2 222 2 222
(352) 3(352)( 3)yxaxaax xaxaax
cc c
N
22 2 2
22
1
(6 5 ) 3 (3 5 2 ) 6
23
похідна
підкореневого
виразу
похідна квадратного
кореня
xaa x x axa x
ax
Після спрощення:
223
22
530 27
3
aaxx
y
ax
c
.
5) Використовуючи формулу (6), одержуємо:
dy
dx
=
2
2
1
x
x
c
§·
¨¸
©¹
=
22 22
22
()( 1) ( 1)
(1)
xx xx
x
cc
=
22
22
2( 1) 2
(1)
x
xxx
x
=
=
33
22
222
(1)
xxx
x
=
22
2
(1)
x
x
.
6)
3
32 32 323
2
4(5 4 8) (5 4 8) 4(5 4 8)
(15 8 ).
похідна основи степеня
похідна степеня
yxx xx xx
xx
cc
u
u
7)
11
1
44 44
3
33
2
3
43
3
42
3
1
(
2
)((
3
)) (
3
)(
2
)
3
14
(3 ) 4 .
3
3(2 )
yx x xx
x
xx
x
cc c c

245
Розділ IV. Диференційне числення функції однієї змінної
8) Використовуючи формулу (8), одержуємо
23 22
26 26 24
2236
((3 5) ) 3(3 5) 6 .
(3 5) (3 5) (3 5)
похідна дробу з
сталим чисельником
x
yx xx
xx x
cc
9) Введемо дробові та від’ємні показники, а потім знайдемо по+
хідну від суми і за формулою (18а), одержимо:
1
2
11
55
1
() (
32 6
)
3 ln3 2 ln2
(
5
)
xx x
xx
fx x
x
c
§·
cc c
¨¸
©¹
1 1
2 2
1
2
1
1 1
5
2 2
1
1
5
2
2
11
6 ln6 3 ln3 2 ln2 ( 5) 6 ln6
2
11
3 ln3 5 2 ln2 6 ln6.
2
xxx
x
xx
x
xx
x
x
x
c
§· § ·
§·
¨¸ ¨ ¸
¨¸
©¹
©¹ © ¹
Обчислюємо
(1)f
c
. Підставимо в значення похідної
х =
1
.
(
1
)
f
c
= –3ln3 –
5ln2
32
+ 3ln6 =
91
32
ln2
.
10) Спочатку знаходимо похідну синуса, а так як синус береться
від 2
х
2
, то знаходимо похідну від 2
х
2
. похідна заданої функції дорів+
нює добутку цих похідних.
2222 2
(sin2 ) cos2 (2 ) cos2 4 4 cos2
y
xxxxxxx
cc c
.
11) Перш за все необхідно продиференціювати тангенс, але так
як він береться від дробу, то слід знайти похідну дробу і одержані
похідні перемножити:
y
c
=
1
tg
x
x
c
§·
¨¸
©¹
=
2
1
1
cos
x
x
1 x
x
c
§·
¨¸
©¹
=
2
1
1
cos
x
x
2
1(1)1xx
x
=
=
2
1
x
2
1
1
cos
x
x
.
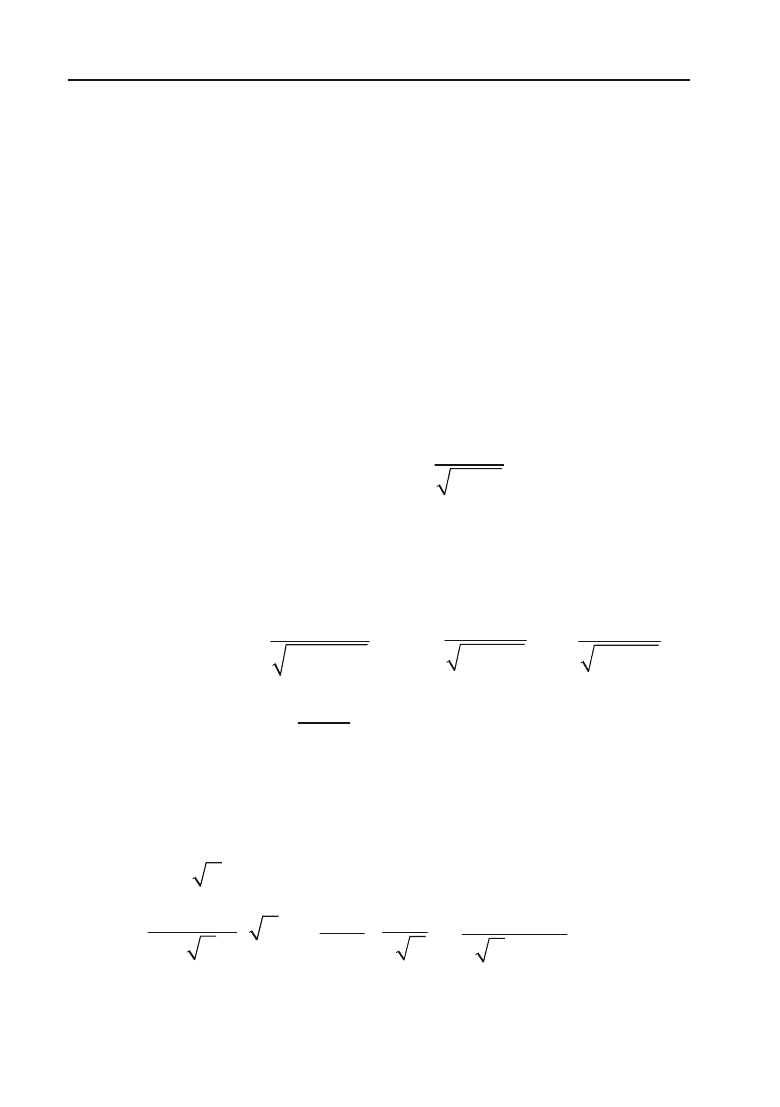
246
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
12)
y
c
=
2
(3sin )
x
c
=
2
3(sin )
x
c
=
32sin
(
sin
)
x
x
c
=
= 6sin
x
cos
x =
3sin2
x.
Сталий множник 3 виносимо за знак похідної. Потім продифе+
ренціюємо степінь, а так як в степінь підноситься sin
x
, то диферен+
ціюємо і sin
x;
знайдені результати перемножуємо.
13)
35 3 5 3 5
(
sin 5 cos 3
)(
sin 5
)
cos 3 sin 5
(
cos 3
)
yxx xxxx
ccc c
=
3sin
2
5
x
(
sin5
)
x
c
cos
5
3
x +
sin
3
5
x
cos
4
3
x
(
cos3
)
x
c
=
=
3sin
2
5
x
cos5
x
5cos
5
3
x +
sin
3
5
x
cos
4
3
x
(–sin3
x
3)
=
=
15sin
2
5
x
cos5
x
cos
5
3
x –
15 sin
3
5
x
cos
4
3
x
sin3
x =
=
15sin
2
5
x
cos
4
3
x
(cos5
x
cos3
x –
sin5
x
sin3
x
) =
=
15sin
2
5
x
cos
4
3
x
cos(5
x+
3
x
)
=
15sin
2
5
x
cos
4
3
x
cos8
x.
14) Розглянемо формулу (14):
2
1
1
x
x
y
u
u
cc
.
Похідна від функції
y =
arcsin
u
знаходиться так: одиниця ділить+
ся на квадратний корінь із одиниці мінус квадрат тої функції, яка
стоїть під знаком арксинуса, і цей дріб помножується на похідну цієї
функції. Через це можна зразу записати:
y
c
=
(
arcsin2
)
x
c
=
2
1
(2 )
1(2)
x
x
c
=
2
1
2
14x
=
2
2
14
x
.
15)
2
1
(arctg )
1
x
xx
y
uu
u
ccc
.
Запам’ятаємо, що похідна функції
y =
arctg
u
дорівнює дробу, в
якому чисельник дорівнює 1, а знаменник дорівнює 1 плюс квадрат
функції, що стоїть під знаком арктангенса, і дріб домножується на
похідну цієї функції.
y =
arctg
x
,
y
c
=
2
1
()
1( )
x
x
c
=
1
1 x
1
2 x
=
1
2(1)
x
x
.
16)
y =
arccos
2
3
x.
247
Розділ IV. Диференційне числення функції однієї змінної
Продиференціюємо спочатку степінь. Так як в степінь підноситься
arccos
3
x
, тобто взяти похідну від arccos3
x
, а потім похідну від 3
х
.
2
(arccos 3 )
y
x
cc
=
2arccos3
x
(
arccos3
)
x
c
=
= 2arccos 3
x
2
1
3
1(3)x
§·
¨¸
¨¸
©¹
=
2
6arccos3
19
x
x
.
17)
y =
arctg
4
3
x
.
y
c
=
4
3
arctg x
c
=
4arctg
3
3
x
3
arctg
x
c
=
= 4arctg
3
3
x
2
3
1
1( )x
§·
¨¸
©¹
3
x
c
=
4arctg
3
3
x
2
3
1
1( )x
§·
¨¸
©¹
1
3
1
1
3
x
=
=
3
3
2
3
4arctg
3(1 )
x
x
2
3
1
x
=
3
3
33
22
4arctg
3(1 )
x
x
x
.
18)
2
sin 3
4
x
y
.
За формулою (18
а
) маємо:
y
c
=
2
sin 3
(4 )
x
c
=
2
sin 3 2
4ln4
(
sin
)
x
x
c
=
2
sin 3
4 ln4 2sin3 (sin3 )
x
xx
c
=
=
2
sin 3
4 ln42sin3cos33
x
x
x
=
2
sin 3
3sin6 4 ln4
x
x
.
19)
2
3xx
ye
.
За формулою (18
б
) маємо:
y
c
=
2
3xx
e
c
=
2
3xx
e
2
3xx
c
=
2
3xx
e
2
1
23xx
2
(
3
)
xx
c
=
=
2
3
xx
e
2
1
23xx
(2
x
+ 1)
=
2
3
2
(2 1)
23
xx
xe
xx
.
20)
3
arcsin
x
ye
.

248
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
y
c
=
3
arcsin
x
e
c
=
3
arcsin
x
e
3
(arcsin )x
c
=
=
3
arcsin
x
e
(–3arcsin
2
x
)
(arcsin )x
c
=
=
3
arcsin
x
e
(–3arcsin
2
x
)
2
1
1( )x
§·
¨¸
¨¸
©¹
x
c
=
=
3
arcsin
x
e
(arcsin
2
x
)
1
1 x
1
2
x
=
3
2arcsin
2
3arcsin
2
x
xe
xx
.
21)
y
= lncos3
x.
За формулою (19
б
), якщо
y =
ln
u
, то
1
y
u
u
cc
. Тобто одержати
похідну від функції ln
u
, де
и
– функція
х
, потрібно одиницю поділи+
ти на функцію
и
, яка стоїть під знаком логарифму, одержаний дріб
слідує помножити на похідну цієї функції.
y
c
=
(lncos3 )
x
c
=
1
cos3x
(
cos3
)
x
c
=
1
cos3x
(–sin
3
x
)
3
=
–3tg3
x.
22)
y
= ln
5
ctg4
x.
Тут спочатку диференціюється степінь логарифму, а потім береть+
ся похідна від логарифмічної функції.
y
c
=
5
(ln ctg4 )
x
c
=
5ln
4
ctg 4
x
(lnctg4 )
x
c
=
= 5ln
4
ctg4
x
1
ctg4
x
2
1
sin 4
x
§·
¨¸
©¹
4
= –
20 ln
4
ctg 4
x
2
sin4 1
cos4
sin 4
x
x
x
§·
¨¸
©¹
=
=
4
20ln ctg 4
sin 4 cos4
x
x
x
=
4
40ln ctg 4
sin 8
x
x
.
23)
2
ln( 1 )
y
xx
.
2
ln 1yxx
c
c
=
2
1
1
x
x
2
1xx
c
=

249
Розділ IV. Диференційне числення функції однієї змінної
=
2
1
1
x
x
2
1
12
21
x
x
§·
¨¸
©¹
=
2
1
1
x
x
2
1
1
x
x
§·
¨¸
©¹
=
=
2
1
1
x
x
2
2
1
1
x
x
x
=
2
1
1
x
.
24)
4
1tg
ln
1tg
y
M
M
.
Спочатку перетворимо задану функцію згідно властивостям ло+
гарифмів, а потім диференціюємо за формулами.
y =
1
4
((ln(1 + tg
M
)
–
ln(1 – tg
M
)).
y
c
=
1
(ln(1 tg ) ln(1 tg ))
4
M
M
c
=
1
(
ln
(
1t
g)
ln
(
1t
g))
4
M
M
cc
=
=
1
4
(
1
1tg
M
(
1t
g)
M
c
–
1
1tg
M
(
1t
g)
M
c
)
=
1
4
1
1tg
M
§
¨
©
2
1
cos
M
§·
¨¸
©¹
–
–
1
1tg
M
2
1
cos
M
·
§·
¸
¨¸
©¹
¹
=
1
4
2
1
cos
M
1tg 1tg
(1 tg )(1 tg )
M
M
M
M
§·
¨¸
©¹
=
=
1
4
2
1
cos
M
2
2
1tg
M
=
1
2
2
22 2
cos
cos (cos sin )
M
M
MM
=
1
2cos2
M
.
25)
y = x
x
.
Задана функція є показникові+степенева функція
y = u
v
,
де
()
ux
M
,
()
vx
\
,
похідна якої знаходиться за формулою:
1
ln
vv
x
xx
y
vu u u uv
ccc
.
1
( ) () ln ()
xx x
y
xxxxxxx
cc c c
= x
x
x–1
1
+ x
x
ln
x
1
=
= x
x
+ x
x
ln
x = x
x
(1 + ln
x
).
250
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
4.1.3. Логарифмічне диференціювання
Якщо необхідно продиференціювати добуток кількох функцій або
дріб, чисельник та знаменник якого містять добуток, часто доцільні+
ше обидві частини виразу спочатку прологарифмувати за основою
е
,
а потім приступити до диференціювання. Цей спосіб одержав назву
логарифмічного диференціювання. Похідна від логарифма функції
називається логарифмічною похідною.
До цього способу зручно прибігати і при дифенеціюванні виразів,
що містять корені із дробів. Цим способом користуються тоді, коли
необхідно продиференціювати функцію виду:
()
(())
x
yx
\
M
,
тобто коли і основа степеня і показник степеня є функцією від
х
.
Приклад 4.3.
Знайти похідну функції:
а)
у
=
(
х
– 1)
2
3
(1)(2)xx
;
б)
y
= (sin
x
)
cosx
.
Розв’язок.
а)
у
= (
х
– 1)
2
3
(1)(2)xx
.
Спочатку прологарифмуємо за основою е обидві частини рівності,
а потім будемо диференціювати.
ln
у
= ln((
х
– 1)
2
3
(1)(2)xx
),
ln
y
= ln(
x
– 1) +
3
2
ln(
x
+ 1) +
1
3
ln(
x
– 2),
31
(ln ) (ln( 1) ln( 1) ln( 2))
23
x
yx x x
cc
,
1
y
y
c
=
1
1x
+
3
2
1
1x
+
1
3
1
1x
=
2
2
231
(1)(2)
xx
xx
,
y
c
= y
2
2
231
(1)(2)
xx
xx
=
2
2
231
(1)(2)
xx
xx
(
х
– 1)
2
3
(1)(2)xx
=
