Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


291
Розділ IV. Диференційне числення функції однієї змінної
E
p
(
q
)
=
6
(2)(8)
p
pp
;
E
p
(
S
)
=
2
21
p
p
.
Для ціни рівноваги
р =
2 маємо:
E
2
(
q
)
= –0,3;
E
2
(
S
)
=
0,8
.
Оскільки отримані значення еластичності за абсолютною вели+
чиною менші одиниці, то і попит, і пропозиція даного товару при
ціні рівноваги нееластичні відносно ціни. Це означає, що зміна ціні
не призведе до різкої зміни попиту і пропозиції.
Так, при збільшенні ціни
р
на 1% попит зменшиться на 0,3%, а
пропозиція збільшиться на 0,8%.
в) При збільшенні ціни
р
на 5% від рівноважної попит зменшуєть+
ся на 5
0,3 = 1,5%, отже, прибуток зростає на 3,5% (5% – 1,5% = 3,5%).
Задача 4.34.
Як пов’язані граничні і середні витрати підприєм+
ства, якщо еластичність повних витрат дорівнює одиниці?
Розв’язок.
Нехай повні витрати підприємства
у
виражаються фун+
кцією
у = f
(
х
), де
х
– обсяг продукції, що випускається. Тоді середні
витрати
у
1
на виробництво одиниці продукції
у
1
=
y
x
.
Таким чином,
Е
х
(
у
1
)
= Е
х
(
x
y
)
= Е
х
(
у
)
– Е
х
(
х
)
= Е
х
(
у
)
–
1.
За умовою
Е
х
(
у
)
=
1, отже
Е
х
(
у
1
)
=
1 – 1 = 0
.
Це означає, що зі
зміною обсягу продукції
х
середні витрати на одиницю продукції не
міняються, тобто
у
1
=
x
y
= с
, звідки
у = сх.
Граничні витрати підприємства визначаються похідною
y
c
c
.
Отже,
1
yy
c
, тобто граничні витрати рівні середнім витратам. (По+
мітимо, що отримане твердження справедливе тільки для лінійних
функцій витрат).
Задача 4.35.
Фірма планує випускати сонячні батареї. На основі
досліджень була встановлена залежність попиту
q
від ціни
р
за батарею:
q =
100 000 – 200
p
,

292
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
де
q —
кількість батарей для продажу в рік. Витрати фірми на ви+
пуск
q
сонячних батарей складають
с =
150 000 + 100
q +
0,003
q
2
.
Розрахувати прибуток, визначити його максимальне значення.
Розв’язок.
Валовий прибуток
R = p – q.
З умови запишемо функцію
р
як функцію змінної
q
:
p =
500 – 0,005
q.
тому
R = R
(
q
)
=
(500 – 0,005
q
)
q.
Тоді прибуток
P
=
R
–
c
.
Отже,
P =
(500 – 0,005
q
)
q –
(150 000 + 100
q
+ 0,003
q
2
)
=
= –
0,008
q
2
+
400
q –
150 000
.
Визначимо максимальний прибуток
()Pq
c
=
–0,016
q +
400,
–0,016
q +
400 = 0,
q =
25 000,
()Pq
cc
=
–0,016 <0.
Отже, при
q =
25 000 одиниць прибуток досягає максимуму,
Р
(25 000)
=
4 850 000 грош. од
.
— максимальне значення прибутку.
Задача 4.36.
Підприємство виробляє
х
одиниць продукції за
ціною
р
(
х
)
=
50 –
1
10
х
, а витрати виробництва задаються функцією
К
(
х
)
=
1
50
х
2
+
14
х +
800.
Знайти оптимальний для підприємства обсяг продукції і відповід+
ний йому максимальний прибуток.
Розв’язок.
Нехай
U
(
х
) — валовий прибуток,
z
(
x
) — прибуток від
реалізації
х
одиниць продукції за ціною
р
(
х
). Тоді
U
(
x
)
= x
p
(
x
);
z
(
x
)
= U
(
x
)
– К
(
х
),
де
p
(
x
),
К
(
х
) — задані функції.
Для розв’язку задачі слід досліджувати функцію
z
(
x
) на екстре+
мум. При цьому прибуток буде максимальним для такого обсягу
х
випуску продукції, для якого
()zx
c
=
0,
()zx
cc
< 0
.
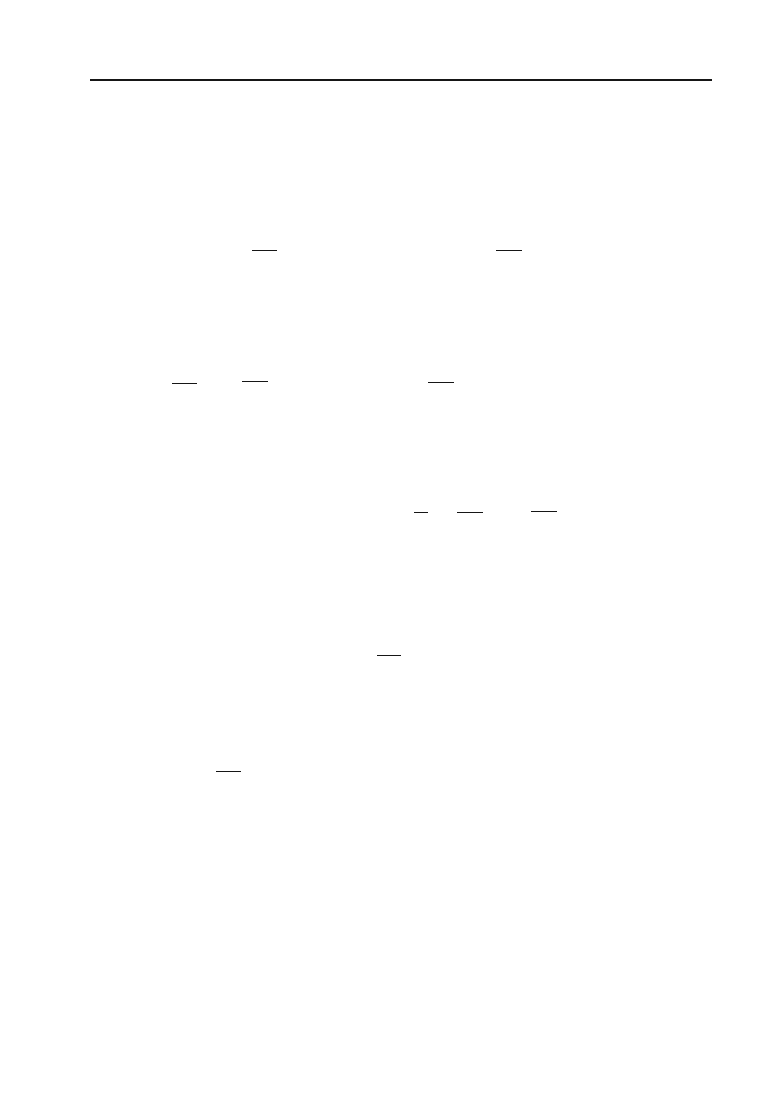
293
Розділ IV. Диференційне числення функції однієї змінної
Проведемо ці дослідження.
1. Формуємо
z
(
x
), знаходимо
()zx
c
і, розв’язавши рівняння
()zx
c
= 0, знаходимо критичну точку.
Врахуємо, що
U
(
x
)
=
50
х –
1
10
х
2
,К
(
х
)
=
1
50
х
2
+
14
х +
800;
z
(
x
)
= U
(
x
)
– К
(
х
);
()zx
c
=
()Ux
c
–
()Кx
c
=
0;
()Ux
c
=
()Кx
c
;
50 –
1
10
х =
1
25
+ 14;
6
25
х
= 36;
х =
150
— критична точка.
2. Знаходимо
()zx
cc
і визначаємо її знак при
х =
150:
()zx
cc
=
()Ux
cc
–
()Кx
cc
=
1
5
–
1
25
= –
6
25
<
0,
x
.
Отже,
х =
150 – точка максимуму функції
z
(
x
), тобто оптималь+
ний обсяг виробництва складає 150 одиниць продукції.
3. Знаходимо максимальний прибуток виробництва, тобто
z
max
=
z
(150).
При
х =
150
ціна
р =
50 –
1
10
150
=
35; валовий прибуток
U =
35
150
=
5250.
Витрати виробництва
К
(
х
)
=
1
50
150
2
+ 14
150 + 800 = 450 + 2100 + 800 = 3350.
Максимальний від продажу прибуток
z
max
= 5250 – 3350 = 1900
.
Задача 4.37.
Виробник реалізує свою продукцію за ціною
р
за
одиницю, а витрати при цьому задаються кубічною залежністю
S
(
x
)
= ax +
O
x
3
(a < p,
O
> 0).
Знайти оптимальний для виробника
обсяг випуску продукції і відповідний йому прибуток.
Розв’язок.
Позначимо обсяг продукції, що випускається, через
х
.
Складемо функцію прибутку
С
(
х
)
= рх –
(
ах +
O
х
3
), де
рх
— валовий
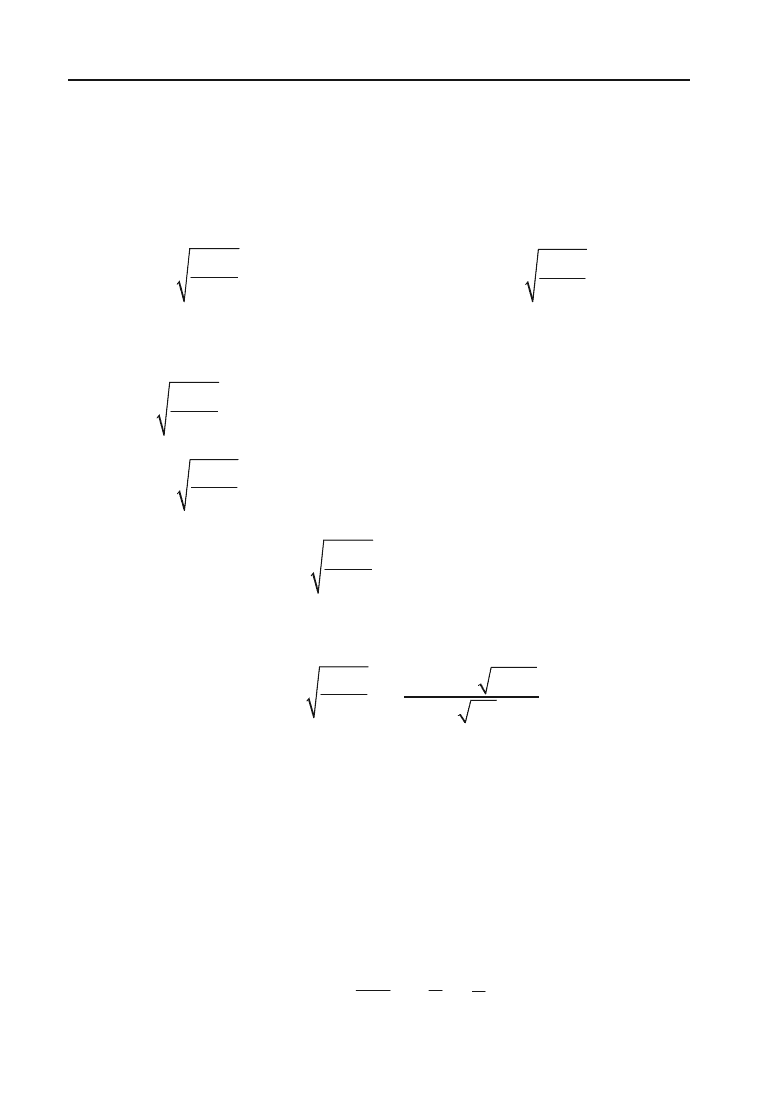
294
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
прибуток від продукції, що реалізується. Досліджуємо цю функцію
на екстремум.
1. Знаходимо
()Cx
c
=
(
р – а
)
–
3
O
х
2
.
2. Знаходимо критичні точки:
()Cx
c
=
(
р – а
)
–
3
O
х
2
=
0,
звідки
х
1
=
3
p
a
O
, (другу критичну точку
х
2
=
3
p
a
O
не розгля+
даємо за змістом задачі).
3. Знаходимо
()Cx
cc
=
6
O
х
і визначаємо знак другої похідної
при
х
1
=
3
p
a
O
;
1
3
p
a
Cx
O
§·
cc
¨¸
¨¸
©¹
< 0
(в даному випадку
()Cx
cc
<
0
при будь яко+
му
х >
0), отже, при
х
1
=
3
p
a
O
прибуток
С
(
х
) максимальний.
4. Знаходимо максимум функції (тобто максимальний розмір при+
бутку)
max 1
3
p
a
Cx
O
§·
¨¸
¨¸
©¹
=
2( )
33
p
apa
O
.
Задача 4.38.
Капітал в 1 млрд. грош. од. може бути розміщений
у банку під 50% річних або інвестований у виробництво, причому
ефективність вкладення очікується у розмірі 100%, а витрати зада+
ються квадратичною залежністю. Прибуток оподатковується в
р
%.
При яких значеннях р вкладення у виробництво є більш ефективни+
ми, ніж чисте розміщення капіталу у банку?
Розв’язок.
Нехай
х
(млрд. грош. од.) інвестується у виробництво,
а 1
–х
— розміщується під відсотки. Тоді розміщений капітал через
рік стане рівним
(1 –
х
)(1 +
50
100
)
=
3
2
–
3
2
х
,
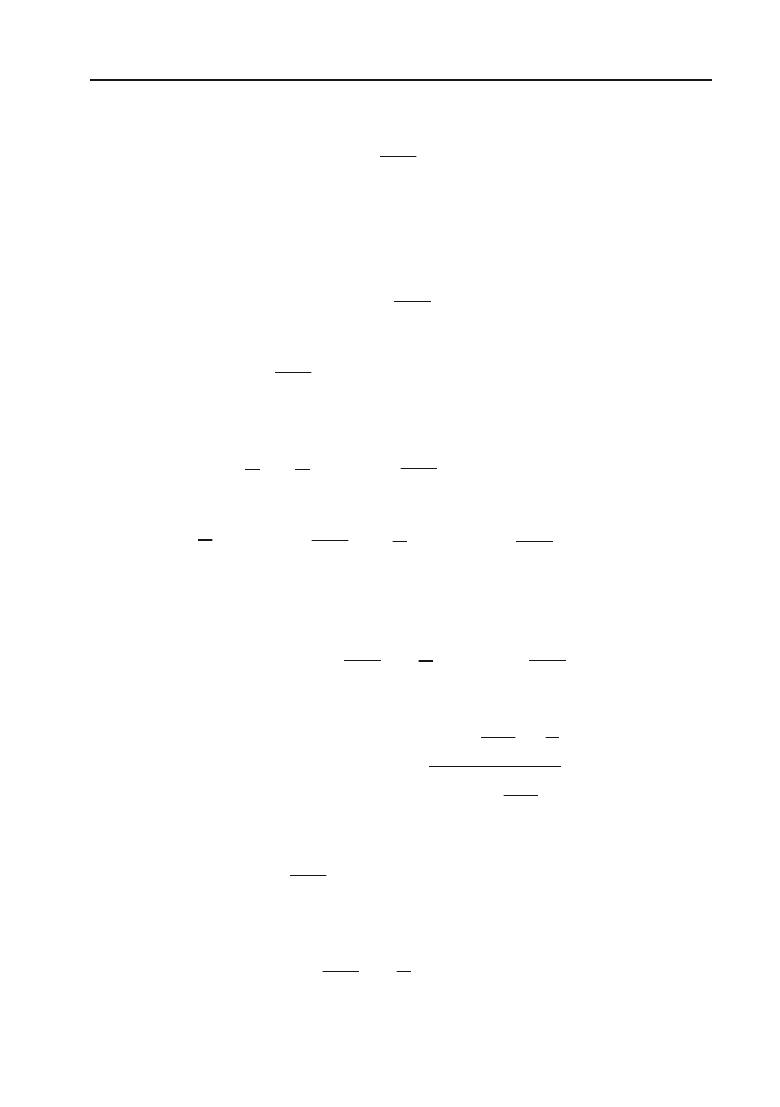
295
Розділ IV. Диференційне числення функції однієї змінної
а капітал, вкладений у виробництво, визначається за формулою
х
(1
+
100
100
)
=
2
х.
Витрати складуть
ах
2
, оскільки за умовою вони задаються квад+
ратичною залежністю, тобто прибуток від вкладення у виробництво
с =
2
х – ах
2
.
Податки складуть (2
х – ах
2
)
100
p
, тобто чистий прибуток вия+
виться рівним (1 –
100
p
)(2
х – ах
2
).
Загальна сума через рік складе:
А
(
х
)
=
3
2
–
3
2
х +
(1 –
100
p
)(2
х – ах
2
)
=
=
3
2
+
[2(1 –
100
p
)
–
3
2
]
x – a
(1 –
100
p
)
x
2
.
Треба знайти максимальне значення цієї функції на відрізку [0, 1].
Маємо
()
A
x
c
=
2(1 –
100
p
) –
3
2
–
2
a
(1
–
100
p
)
x
;
()
A
x
c
=
0
при
х
0
=
3
21
100 2
21
100
p
p
a
§·
¨¸
©¹
§·
¨¸
©¹
;
()
A
x
cc
= –
2
а
(1
–
100
p
) < 0, тобто
х
0
—
точка максимуму.
Щоб
х
0
[0, 1]? Необхідно виконати умову
0 < 2(1 –
100
p
) –
3
2
< 1, або
р
< 25.

296
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Таким чином, якщо
р >
25, то вигідніше нічого не вкладати у
виробництво і розмістити весь капітал у банку. Якщо
р
< 25, то мож+
на показати, що при
х = х
0
А
(
х
0
)
=
3
2
+
2
3
21
100 2
41
100
p
p
a
ªº
§·
¨¸
«»
©¹
¬¼
§·
¨¸
©¹
>
3
2
= А
(0).
Тобто вкладання у виробництво вигідніше, ніж чисте розміщен+
ня під відсотки.
4.7.5. Задачі для самостійного розв’язку
Задача 4.39.
Розрахувати еластичність даних функцій і знайти
значення показника еластичності для заданих
х
:
1)
y
= 1 + 2
x
–
x
2
,
x
= 1;
2)
y
=
e
5x
,
x
= 1,
x
= 0,
x
= 2;
3)
y
= 5ln
x
,
x
= 10,
x
=
e
,
x
=
e
4
;
4)
y
=
x
2
x
e
,
x
= 1,
x
= 2.
Задача 4.40.
Крива повних витрат
К
(
х
). Визначити: а) криву гра+
ничних витрат; б) розрахувати коефіцієнт еластичності при заданих
значеннях
х
, де
х
— обсяг виробництва, якщо:
1)
К
(
х
) = 150
х
–
х
2
+
3
100
x
,
x
= 10,
х
= 50;
2)
К
(
х
) =
х
3
– 3
х
2
+ 10
х
,
x
= 1,
x
= 2.
Задача 4.41.
Функцією середніх витрат називається функція
S
=
()fx
x
, де
f
(
x
) — повні витрати виробництва,
х
— кількість оди+
ниць продукції виражаються формулою
у
=
х
3
+ 3
х
2
+ 10
х
. Необ+
хідно знайти: а) обсяг виробництва, при якому середні витрати бу+
дуть лінійними; б) побудувати криві повних, середніх і граничних
витрат.

297
Розділ IV. Диференційне числення функції однієї змінної
Задача 4.42.
Цукровий завод виробляє
х
одиниць продукції в
місяць, а сумарні витрати виробництва
К
(
х
) =
2
50
x
+ 5
х
+ 300. За+
лежність між питомою ціною
р
і кількістю одиниць продукції
х
, що
можна продавати за цією ціною така:
р
(
х
) = 40 –
10
x
. Розрахувати,
за яких умов прибуток буде максимальним (валовий прибуток
U
(
x
) =
x
p
(
x
), прибуток
z
(
x
) =
U
(
x
) –
К
(
х
)).
Задача 4.43.
Залежність між витратами виробництва
у
(грош. од.)
і обсягом продукції, що випускається
х
(од.), виражається функцією
у
= 10
х
– 0,04
х
3
. Визначити середні та граничні витрати при обсязі
продукції рівному 5 од.
Задача 4.44.
Залежність попиту
q
від ціни р виражається функцією
q
(
p
) = –2
p
2
+ 3
p
+ 8. Знайдіть еластичність
Е
р
(
q
) попиту
q
відносно
ціни
р
і значення показника еластичності при
р
= 1. Зробити висновок.
Задача 4.45.
Функції попиту
q
і пропозиції
S
від ціни р задають+
ся відповідно рівняннями:
q
= 7 –
р
і
S
=
р
+ 1. Знайти: а) ціну рівно+
ваги; б) еластичність попиту і пропозиції для цієї ціни; в) зміну при+
бутку (у відсотках) при збільшенні ціни на 5% від ціни рівноваги.
Задача 4.46.
Дана функція
К
(
х
) повних витрат виробництва.
Знайти: а) обсяг виробництва, при якому середні витрати будуть
мінімальні; б) побудувати криві повних, середніх і граничних витрат
виробництва; в) розрахувати коефіцієнт еластичності при заданих
значеннях
х
, де
х
— обсяг виробництва, якщо:
1)
К
(
х
) =
2
4
x
+
х
+ 100,
x
= 2,
х
= 50;
2)
К
(
х
) = 100 +
2
25
x
,
x
= 5,
x
= 25.
Задача 4.47.
Крива повних витрат має вигляд
К
(
х
) =
х
3
– 6
х
+ 15
х
(
х
— обсяг виробництва). Розрахувати, при якому обсязі виробниц+
тва середні витрати мінімальні.

298
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§4.8. Дослідження функцій та побудова їх графіків
4.8.1. Зростання та спадання функції.
Функція
f
(
x
) називається строго зростаючою на проміжку (
а
,
b
),
якщо для будь+яких двох чисел х
1
і х
2
із цього проміжку із нерівності
х
2
>
х
1
слідує нерівність
f
(
x
2
) >
f
(
x
1
),
Якщо ж із нерівності
х
2
>
х
1
слідує нестрога нерівність
f
(
x
2
)
t
f
(
x
1
),
то функція називається зростаючою на даному проміжку.
Функція
f
(
x
) називається строго спадною на заданому проміжку
(
а
,
b
), якщо для будь+яких двох чисел
х
1
і
х
2
із цього проміжку із
нерівності
х
2
>
х
1
слідує нерівність
f
(
x
2
) <
f
(
x
1
),
Якщо ж із нерівності
х
2
>
х
1
слідує нестрога нерівність
f
(
x
2
)
d
f
(
x
1
),
то функція називається спадною на даному проміжку.
Функції зростаючі та спадані, а також функції строго зростаючі
та строго спадані називаються монотонними.
Якщо у всіх точках деякого інтервалу перша похідна
()
f
x
c
> 0,
то функція
f
(
x
) на цьому інтервалі зростає. Якщо у всіх точках дея+
кого інтервалу перша похідна
()
f
x
c
< 0, то функція
f
(
x
) на цьому
інтервалі спадає.
Це є достатня ознака зростання та спадання функції на інтервалі.
Точка
х
=
х
0
називається критичною точкою першого роду, або
просто критичною, якщо має місце одна із умов:
1)
0
()
f
x
c
= 0;
2)
0
()
f
x
c
=
f
;
3) функція
()
f
x
c
визначена в точці
х
=
х
0
, але
0
()
f
x
cc
не існує.
Щоб знайти інтервали монотонності функції
f
(
x
), необхідно на
числову вісь нанести граничні точки області визначення функції на
всі її критичні точки.
Область визначення при цьому розіб’ється на деяке число
інтервалів, на кожному із яких похідна не змінює знак. Це і бу+
дуть інтервали монотонності функції. Для того щоб узнати, спа+
дає чи зростає функція на заданому інтервалі монотонності, дос+
татньо з’ясувати, який знак має похідна в будь+якій точці цього
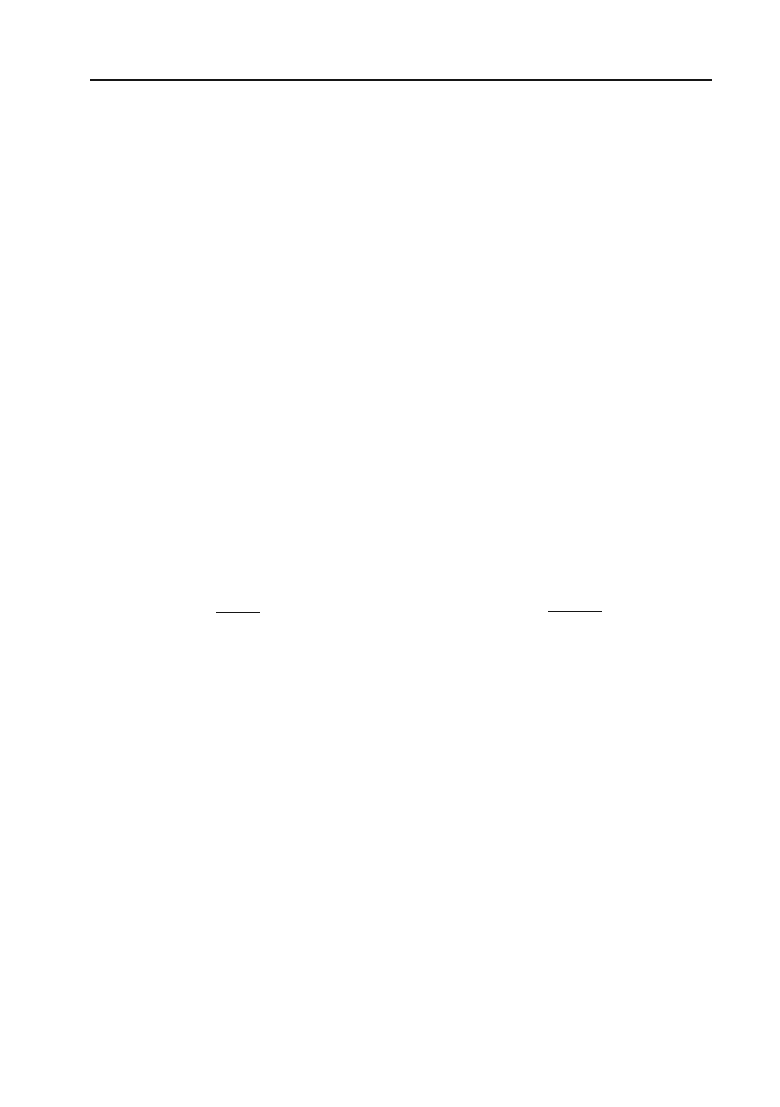
299
Розділ IV. Диференційне числення функції однієї змінної
інтервалу. Якщо в цій точці
()
f
x
c
> 0 , то функція зростає, якщо
()
f
x
c
< 0 — спадає.
Приклад 4.48.
Визначити інтервали зростання та спадання
функцій:
а)
f
(
x
)
= x
3
–
12
x +
11; б)
y =
ln(1 –
x
2
).
Розв’язок.
а) Областю існування функції
f
(
x
)
= x
3
– 12
x
+ 11
являється вся
вісь
Ох
(функція існує при будь+якому значенні
х
). Знайдемо по+
хідну функції
()
f
x
c
=
3
x
2
–
12;
х
2
= 4;
х =
r
2
.
Точки
х =
r
2 розбивають область визначення на інтервали
(
f
; –2),
(
–
2; 2), (2;
f
).
Знаходимо знак функції в кожному інтервалі
(
3
)
f
c
>
0;
(
0
)
f
c
< 0;
(
3
)
f
c
> 0. Отже, (
f
; –2) і (2;
f
) – інтервали зростання функції,
а (–2; 2) – інтервал спадання функції.
б) Областю існування функції
y =
ln(1 –
x
2
) є інтервал (–1; 1).
Похідна
2
1
y
x
c
.
Знаходимо критичні точки:
2
2
1
x
x
=
0,
х =
0
.
В інтервалі (–1; 0)
y
c
> 0, а це означає, що (–1; 0) є інтервалом зро+
стання функції. В інтервалі (0; 1)
y
c
< 0, а це означає, що (0; 1)
є
інтервал спадання функції.
Задача 4.49.
Витрати виробництва
К
залежать від обсягу про+
дукції
х
за формулою
К
(
х
)
=
–0,05
х
3
+
33375
х +
250. При яких зна+
ченнях
х
витрати виробництва почнуть спадати?
Розв’язок.
Знайдемо похідну
()
Кx
c
= –0,15
х
2
+
33375
.
Витра+
ти спадають, коли
()
Кx
c
< 0, тобто –0,15
х
2
+ 33375 < 0
.
Звідси
0,15
х
2
– 33375 > 0, або
х
2
– 22500 > 0. Нерівність виконується, якщо
х <
–150 або
х
> 150.
За умовою задачі
х
< 0 не може бути розв’яз+
ком. Отже, витрати виробництва починають спадати при обсягах
х
> 150.

300
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
4.8.2. Означення максимуму та мінімуму функції.
Найбільше та найменше значення функції на відрізку
Функція
f
(
x
) має в точці
х
=
х
0
максимум, якщо значення функції
в цій точці більше, ніж її значення в усіх точках, достатньо близьких
до
х
0
.
Тобто, функція f(x) має максимум при
х
=
х
0
, якщо
f
(
x
0
+
x
'
) <
f
(
x
0
),
для будь+якого
x'
— як додатного, так і від’ємного, але достатньо
малих за абсолютною величиною.
Функція
f
(
x
) має в точці
х
=
х
0
мінімум, якщо значення функції
в цій точці менше, ніж її значення в усіх точках, достатньо близьких
до
х
0
.
Тобто, функція
f
(
x
) має мінімум при
х
=
х
0
, якщо
f
(
x
0
+
x
'
) >
f
(
x
0
),
для будь+якого
x'
— як додатного, так і від’ємного, але достатньо
малих за абсолютною величиною.
Якщо в деякій точці функція має максимум або мінімум, то гово+
рять, що в цій точці має місце екстремум.
В економічних дисциплінах екстремумом функції називають її
локальним оптимумом, а процес знаходження екстремального зна+
чення функції називають оптимізацією.
Слід пам’ятати:
1) Максимум (мінімум) не являється обов’язково найбільшим
(найменшим) значенням, що приймає функція. Поза розглянутого
околу точки
х
0
функція може приймати більші (менші) значення, ніж
в цій точці.
2) Функція може мати декілька максимумів і мінімумів.
3) Функція, що визначена на відрізку, може досягнути екстрему+
му тільки у внутрішніх точках цього відрізка.
Необхідна умова екстремуму.
Якщо функція
f
(
x
)
має екстремум при
х = х
0
, то її похідна в цій
точці дорівнює нулю, або нескінченості, або взагалі не існує.
Із цього слідує, що точки екстремуму функції необхідно знаходи+
ти тільки серед тих, в яких її перша похідна
()
f
x
c
=
0, або не існує.
Слід уяснити, що вказана ознака екстремуму є тільки необхідною,
але не достатньою.
