Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

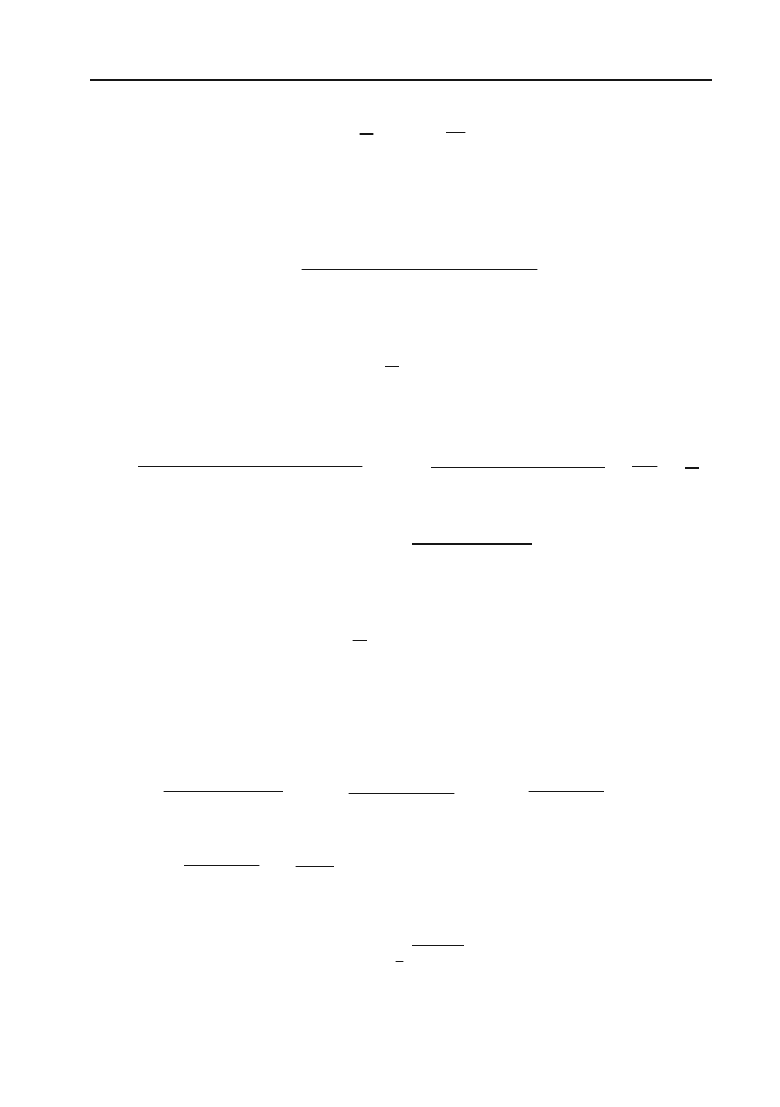
271
Розділ IV. Диференційне числення функції однієї змінної
також буде являти випадок
0
0
½
®¾
¯¿
або
f
½
®¾
f
¯¿
, то можна знову застосу+
вати правило Лопіталя, якщо це корисно, до одержання результату.
Приклад 4.22.
Знайти границю:
1
lim
xo
32
43 2
528
216215
xxx
xx xx
.
Розв’язок.
Якщо в заданий дріб підставити –1 замість
х
, то одер+
жимо «невизначеність» виду
0
0
½
®¾
¯¿
. Застосуємо правило Лопіталя
одержуємо:
1
lim
x
o
32
43 2
528
216215
xxx
xx xx
=
1
lim
x
o
2
32
3102
46322
xx
xx x
=
15
24
=
5
8
.
Приклад 4.23.
Обчислити
0
lim
xo
2
sin
xx
ee x
xx
.
Розв’язок.
Якщо замінити в даному дробу
х
нулем, то одержує+
мо «невизначеність» виду
0
0
½
®¾
¯¿
. Застосуємо правило Лопіталя: за+
мінимо чисельник і знаменник дробу їх похідними, потім ще раз і
ще раз їх похідними і прийдемо до знаходження границі нового
відношення.
0
lim
xo
2
sin
xx
ee x
x
x
=
0
lim
xo
2
1cos
xx
ee
x
=
0
lim
xo
sin
x
x
ee
x
=
=
0
lim
xo
cos
x
x
ee
x
=
11
1
=
2
.
Приклад 4.24.
Обчислити
2
lim
x
S
o
tg 3
tg5
x
x
.
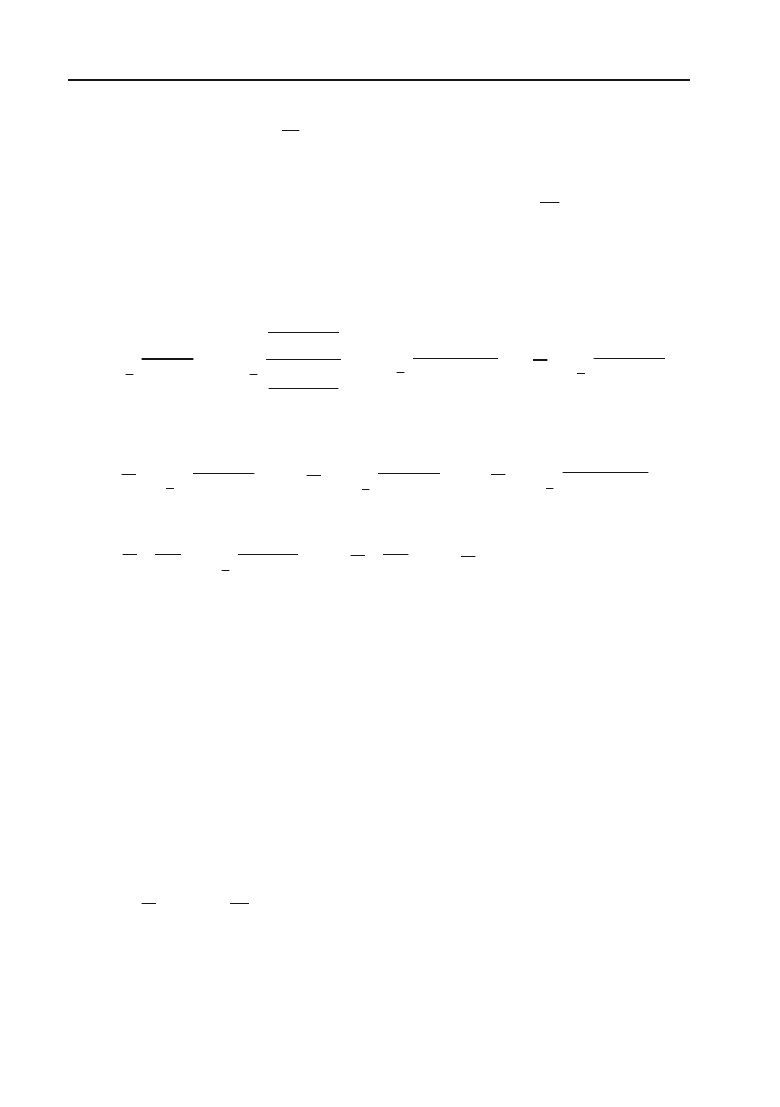
272
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Розв’язок.
При
2
x
S
o
функції tg 3
x
i tg 5
x
— величини нескінчен+
но великі, тобто ми маємо «невизначеність» виду
f
½
®¾
f
¯¿
. Застосуємо
правило Лопіталя, тобто замінимо відношення функції відношенням
їх похідних і будемо знаходити границю цього нового відношення.
2
lim
x
S
o
tg 3
tg5
x
x
=
2
lim
x
S
o
2
2
3
cos 3
5
cos 5
x
x
=
2
lim
x
S
o
2
2
3cos 5
5cos 3
x
x
=
3
5
2
lim
x
S
o
2
2
cos 5
cos 3
x
x
=
=
3
5
2
lim
x
S
o
2
cos5
cos3
x
x
§·
¨¸
©¹
=
3
5
2
lim
x
S
o
§
¨
©
2
cos5
cos3
x
x
·
¸
¹
=
3
5
2
lim
x
S
o
§
¨
©
2
5sin5
3sin3
x
x
·
¸
¹
=
=
3
5
25
9
2
lim
x
S
o
§
¨
©
2
sin5
sin 3
x
x
·
¸
¹
=
5
3
2
1
1
§·
¨¸
©¹
=
5
3
.
4.5.2. Випадки
0
f
та
ff
Випадки знаходження границь
3)
^
`
0
f
— коли функція являє добуток нескінченно малої ве+
личини на нескінченно велику величину;
4)
^
`
ff
— коли функція являє різницю двох додатних не+
скінченно великих величин.
В цих випадках знаходження границі функції зводиться до ви+
падку
0
0
½
®¾
¯¿
або
f
½
®¾
f
¯¿
шляхом перетворення функції до виду дробу.
Приклад 4.25.
Знайти границі:
1)
0
lim ctg2
x
x
x
o
;
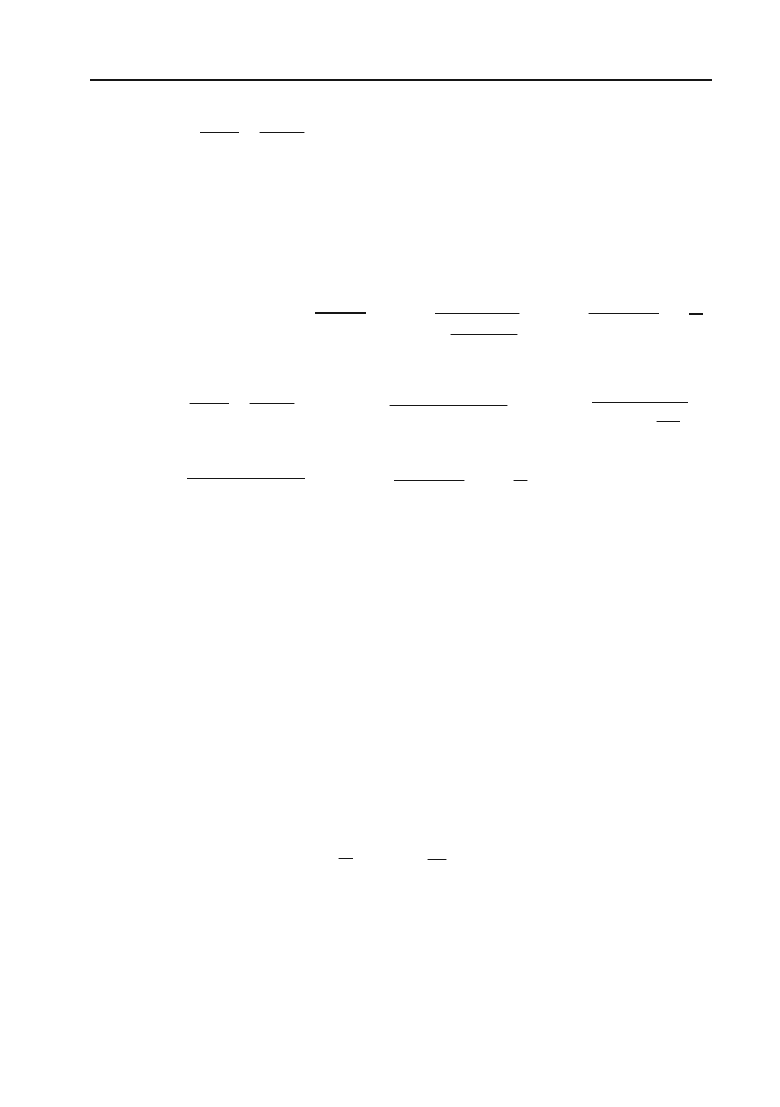
273
Розділ IV. Диференційне числення функції однієї змінної
2)
1
lim
xo
1
ln 1
x
xx
§·
¨¸
©¹
.
Розв’язок.
Встановивши, що має місце випадок
0
f
або
ff
,
перетворимо функцію до виду дробу, чисельник і знаменник якого
одночасно прямують до нуля або до нескінченості, а потім застосо+
вують правило Лопіталя:
1)
0
lim ctg2
x
x
x
o
=
0
lim
xo
tg2
x
x
=
0
lim
xo
2
1
1
2
cos 2
x
=
0
lim
xo
2
cos 2
2
x
=
1
2
.
2)
1
lim
xo
1
ln 1
x
xx
§·
¨¸
©¹
=
1
lim
xo
1ln
(1)ln
x
xx
x
x
§·
¨¸
©¹
=
1
lim
xo
1
1ln 1
ln
x
x
x
x
=
=
1
lim
xo
ln
ln 1
xx
xxx
=
1
lim
xo
1ln
2ln
x
x
=
1
2
.
4.5.3. Випадки
1
f
,
0
f
та
0
0
Випадки знаходження границі:
5)
1
f
— коли функція являє степінь, основа якого прямує до оди+
ниці, а показник — до нескінченності;
6)
0
f
— коли функція являє степінь, основа якого прямує до не+
скінченності, а показник – до нуля;
7) 0
0
— коли функція являє степінь, основа та показник якої пря+
мує до нуля.
Ці випадки знаходження границі функції зводяться до випадків
0
f
а потім до випадку
0
0
½
®¾
¯¿
або
f
½
®¾
f
¯¿
наступним шляхом: функ+
ція логарифмується та спочатку знаходять границю її логарифма, а
потім за знайденою границею логарифма знаходять і границю самої
функції.
Приклад 4.26.
Знайти границі:
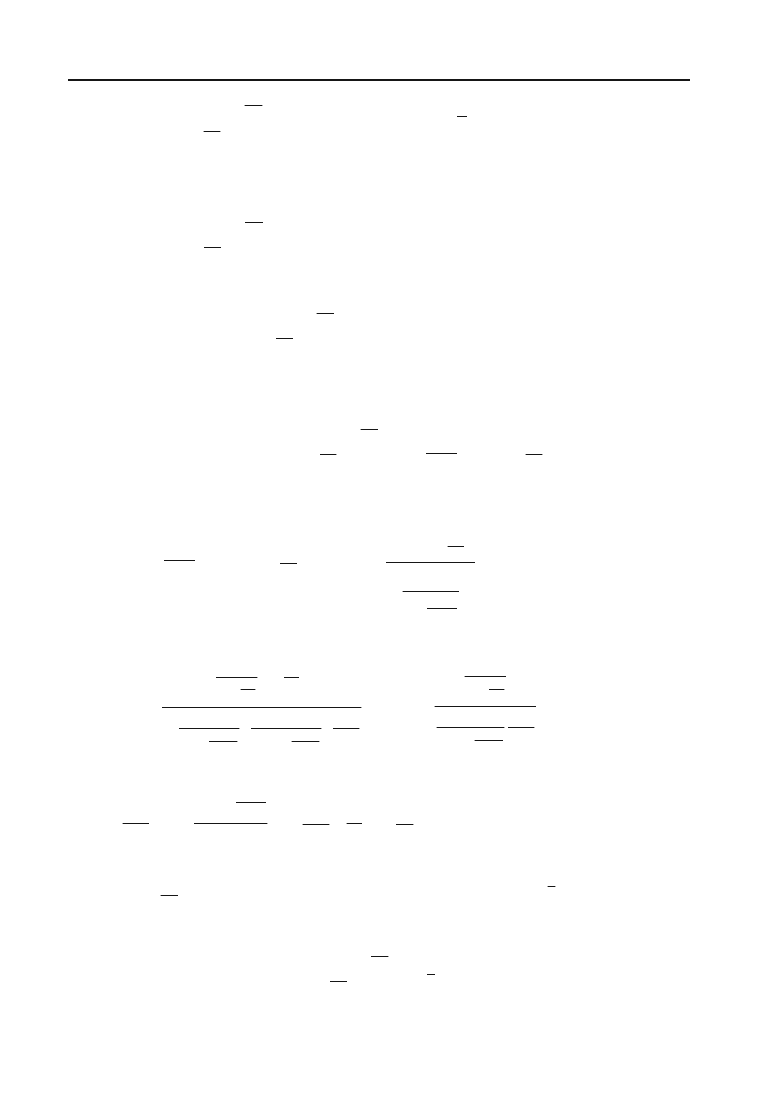
274
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
1)
tg
2
lim 2
x
a
xa
x
a
S
o
§·
¨¸
©¹
;2)
1
lim (ln )
x
x
x
of
.
Розв’язок.
1)
tg
2
lim 2
x
a
xa
x
a
S
o
§·
¨¸
©¹
. Встановивши, що має місце випадок
1
f
, по+
значимо, що
tg
2
2
x
a
x
y
a
S
§·
¨¸
©¹
. Потім прологарифмуємо отриману
функцію:
ln
у =
tg
2
ln 2
x
a
x
a
S
§·
¨¸
©¹
=
tg
2
x
a
S
ln(2 –
x
a
).
Знайдемо границю її логарифма
lim
x
ao
tg
2
x
a
S
ln
(2
–
x
a
)
=
lim
x
ao
ln(2 )
1
tg
2
x
a
x
a
S
=
=
lim
x
ao
22
12
()
2
11
()
tg cos
2
22
a
x
a
xx
a
aa
S
SS
=
lim
x
ao
2
1
2
1
sin
2
2
x
a
x
a
a
S
S
=
=
2a
S
lim
x
ao
2
sin
2
2
x
a
ax
S
=
2a
S
1
a
=
2
S
.
2
ln y
S
. Знаходимо границі функції
lim
xa
y
o
=
2
e
S
.
Отже,
tg
2
lim 2
x
a
xa
x
a
S
o
§·
¨¸
©¹
=
2
e
S
.
275
Розділ IV. Диференційне числення функції однієї змінної
2)
1
lim (ln )
x
x
x
of
. Встановивши, що має місце випадок
0
f
, вико+
наємо перетворення:
у =
1
(ln )
x
x
; ln
y =
ln
1
(
ln
)
x
x
=
1
x
ln ln
x
;
lim
x of
(ln
y
)
=
lim
x of
lnln x
x
=
lim
xof
1
lnxx
= 0,
lim
xof
(ln
y
)
= 0;
lim
x
y
of
= e
0
=
1,
Отже,
1
lim
(
ln
)
x
x
x
of
=
1.
4.5.4. Приклади для самостійного розв’язку
Приклад 4.27.
Знайти границі:
1)
0
lim
x
o
1
sin
x
e
x
;2)
0
lim
x
o
sin
tg
x
x
x
x
;
3)
0
lim
x
o
sin cos
xx
ee
xx
;4)
0
lim
xo
32
2
1
62
cos 1
2
x
xx
ex
x
x
;
5)
0
lim
x
o
ln
lnsin
x
x
;6)
lim
x
of
(
x
n
e
–x
);
7)
lim
x of
((
S
– 2arctg
x
)ln
x
); 8)
lim
x
of
(
x
(e
1/x
– 1));
9)
0
lim
x
o
tg
1
x
x
§·
¨¸
©¹
; 10)
lim
x
of
(
е
х
+
х
)
1/х
.

276
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§4.6. Деякі основні теореми диференційного числення
4.6.1. Теорема Лагранжа (про скінчені прирости функції)
Якщо функція
у
=
f
(
x
) неперервна на відрізку [
a
;
b
] і диференц+
ійовна на інтервалі (
а
,
b
), то всередині цього інтервалу існує хоча б
одна точка
с
(
a
<
c
<
b
) така, що виконується рівність:
() ()
()
fb fa
fc
ba
c
.
Економічний зміст теореми Лагранжа.
Нехай
у = f
(
x
) виражає залежність випуску
у
від витрат
х
деяко+
го специфічного ресурсу. Якщо об’єм витрат збільшується від
а
до
b
одиниць, то різниця
f
(
b
)
– f
(
a
) виражає відповідну зміну випуску.
Відношення
() ()fb fa
ba
показує, на скільки одиниць в середньому
змінюється випуск продукції, якщо витрати виросли на одну одини+
цю. Іншими словами,
() ()fb fa
ba
— середнє виробництво ресурсу
на проміжку [
a
;
b
].
Граничне виробництво ресурсу дорівнює значенню похідної
функції випуску при даному рівні витрат. Якщо витрати ресурсу
складають
с
одиниць, то
()
f
c
c
— відповідне їм граничне відношення
ресурсу.
На основі теореми Лагранжа можна стверджувати, що для про+
цесу виробництва, який описаний функцією випуску
у = f
(
x
), котра
неперервна на відрізку [
a
;
b
] і диференційована на (
а, b
), існує хоча
б один граничний рівень витрат
с
, при якому граничне виробництво
відповідного ресурсу співпадає з його середнім виробництвом.

277
Розділ IV. Диференційне числення функції однієї змінної
4.6.2. Формула Тейлора
Функція
f
(
x
), що диференційована (
n
+ 1) раз в деякому інтер+
валі, якому належить точка а, може бути представлена в вигляді суми
многочлена
n
+го ступеня та залишкового члену
R
n
:
f
(
x
) =
f
(
a
) +
()
1!
fa
c
(
x
–
a
) +
()
2!
fa
cc
(
x
–
a
)
2
+
()
3!
fa
ccc
(
x
–
a
)
3
+ … +
+
()
()
!
n
f
a
n
(
x
–
a
)
n
+
R
n
,
(Т)
R
n
=
(1)
()
(1)!
n
f
c
n
(
x
–
a
)
n+1
,
де
с
– деяке значення між
а
і
х
.
с
=
а
+
T
(
х
–
а
), 0 <
T
< 1.
Формула Тейлора (Т) дозволяє наближено представити (апрок+
симувати) довільну функцію
f
(
x
) у вигляді многочлену:
f
(
x
) =
f
(
a
) +
()
1!
fa
c
(
x
–
a
) +
()
2!
fa
cc
(
x
–
a
)
2
+
()
3!
fa
ccc
(
x
–
a
)
3
+ … +
+
()
()
!
n
f
a
n
(
x
–
a
)
n
,
(що називається
многочленом Тейлора
) і разом із тим дозволяє оці+
нити похибку
,
яка при цьому виникає. Похибка
R
n
в багатьох випад+
ках може бути зробленою як завгодно малою. Через це формула
Тейлора (Т) є однією із найважливіших формул математичного ана+
лізу, яка широко застосовується і як тонкий інструмент теорії дослід+
ження, і як засіб розв’язку практичних задач.
Частинний, найпростіший вигляд формули Тейлора при
а
= 0
прийнято називати
формулою Маклорена
:
f
(
x
)
= f
(0)
+
(0)
1!
f
c
x +
(0)
2!
f
cc
x
2
+
(0)
3!
f
ccc
x
3
+ … +
()
(0)
!
n
f
n
x
n
+
+ R
n
(М)

278
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
4.6.3. Застосування формули Тейлора в економічних задачах
Наближена рівність
f
(
x
) =
T
2
(
x
) =
f
(
a
) +
()
1!
fa
c
(
x
–
a
) +
()
2!
fa
cc
(
x
–
a
)
2
застосовується в задачах економічної статистики. Наприклад розг+
лянемо таку задачу: припустимо, що для чисел введено середнє ариф+
метичне
а
=
123
...
n
xxx x
n
і середнє квадратичне відхилення
22 2
12
( ) ( ) ... ( )
n
xa xa xa
n
V
.
Як визначити середнє арифметичне виду
123
( ) ( ) ( ) ... ( )
n
fx fx fx fx
y
n
,
якщо числа
х
1
,
х
2
,
х
3
, … ,
х
n
невідомі, але відомий відрізок, якому вони
належать.
Значення
y
можна, очевидно, знайти наближено. Підставимо
замість
f
(
x
) многочлен Тейлора другого порядку в точці
а
.
y
=
1
n
1
(
n
i
¦
f
(
a
) +
()
1!
fa
c
(
x
–
a
) +
()
2!
fa
cc
(
x
–
a
)
2
) =
=
1
n
n f
(
a
) +
()
f
a
c
(
1
n
1
n
i
i
x
¦
–
1
n
na
) +
1
2n
()
f
a
cc
2
1
()
n
i
i
xa
¦
.
R
n
=
(1)
()
(1)!
n
f
x
n
4
x
n+1
.
Формула Маклорена (М) дає розклад функції по степеням самої
незалежної змінної.
279
Розділ IV. Диференційне числення функції однієї змінної
4.6.4. Розклад основних елементарних функцій
за формулою Тейлора
1. Розкладемо за формулою Тейлора функцію
у
=
е
х
у точці
х
0
=
а
= 0. Для цього обчислимо:
y = e
x
,
y
(0) = 1;
y
c
= e
x
,
(
0
)
y
c
=
1;
y
cc
= e
x
,
(
0
)
y
cc
=
1;
……… ………
y
(n)
= e
x
,
y
(n)
(0)
=
1.
Далі за формулою Тейлора маємо:
e
x
= 1 +
1
1!
х
+
1
2!
х
2
+
1
3!
х
3
+ ... +
1
!n
х
n
+
(
1
)
!
x
e
n
T
x
n+1
,
0 <
T
< 1.
2. Розкладемо за формулою Тейлора функцію
y =
sin
x
у точці
x
0
= a =
0. Насамперед знайдемо
y =
sin
x
;
y
(0)
=
0;
y
c
=
cos
x
;
(
0
)
y
c
=
1;
y
cc
= –
sin
x
;
(
0
)
y
cc
=
0;
y
ccc
= –
cos
x
;
(
0
)
y
ccc
= –
1;
y
(iv)
=
sin
x
;
y
(iv)
=
0;
……… ………
За формулою Тейлора дістаємо:
sin
x
=
1
1!
х –
1
3!
х
3
+
1
5!
х
5
–
1
7!
х
7
+
1
9!
х
9
– … +
(–1)
2n+1
1
(2 1)!
n
x
2n+1
+
Оскільки
1
2n
()
f
a
cc
2
1
()
n
i
i
x
a
¦
=
2
1
2
V
,
маємо
y
=
f
(
a
) +
2
1
2
V
.
280
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
+ (–1)
n+1
23
sin( )
2
(2 3)!
n
x
n
TS
x
2n+1
,
0 <
T
< 1
.
3. Розклад за формулою Тейлора функції
у =
cos
x
в точці
х
0
= 0.
Насамперед обчислимо:
y =
cos
x
;
y
(0)
=
1;
y
c
=
–sin
x
;
(0)
y
c
=
0;
y
cc
= –
cos
x
;
(
0
)
y
cc
=
–1;
y
ccc
=
sin
x
;
(
0
)
y
ccc
=
0;
y
(iv)
=
cos
x
;
y
(iv)
=
1;
……… ………
Далі за формулою Тейлора (Т) дістаємо:
cos
x
= 1
–
1
2!
х
2
+
1
4!
х
4
–
1
6!
х
6
+
1
8!
х
8
–
… +
(–1)
n
1
(2 )!
n
x
2n
+
+ (
–
1)
n+1
cos( ( 1) )
(2 2)!
xn
n
TS
x
2n+2
,
0 <
T
< 1
.
4. Розклад функції
(1 )
y
x
P
, де
m
— довільне число. Наприклад:
(1 )
y
x
P
;
y
(0) = 1;
1
(1 )
yx
P
P
c
;
(0)
y
P
c
;
2
(
1
)(
1
)
yx
P
PP
cc
;
(0) ( 1)
y
P
P
cc
;
3
(
1
)(
2
)(
1
)
yx
P
PP P
ccc
;
(0) ( 1)( 2)
y
P
PP
ccc
;
............ ...........
За формулою Тейлора (Т) отримаємо розклад:
(1 )
x
P
=
1
+
1!
P
х +
(1)
2!
PP
х
2
+
(1)(2)
3!
PP P
х
3
+ ... +
+
( 1)( 2)...( 1)
!
k
k
PP P P
х
k
+ ...
