Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.


281
Розділ IV. Диференційне числення функції однієї змінної
Цей ряд названо
формулою бінома Ньютона
на честь її відкрива+
ча. Якщо
P
— натуральне число, то ряд містить скінчене число до+
данків.
5. Розклад функції
у =
ln(1 +
x
)
.
Наприклад:
y =
ln(1+
x
);
y
(0) = 0;
y
c
=
1
1 x
;
(0)
y
c
= 1;
y
cc
= (–1)
2
1
(1 )
x
;
(0)
y
cc
=
–1;
y
ccc
=
(–1)(–2)(1+
х
)
–3
;
(0)
y
ccc
=
2!;
y
(iv)
=
(–1)(–2)(–3)(1+
х
)
–4
;
y
(iv)
=
–3!;
……… ………
ln(1+
x
)
=
1
1!
х –
1
2!
х
2
+
2!
3!
х
3
+ ... +
1
1
n
(1)!
!
n
n
х
n
або
ln(1+
x
)
= х –
1
2
х
2
+
1
3
х
3
+ ... + х
n
+ R.

282
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§4.7. Економічний зміст похідної. Еластичність
4.7.1. Задача на продуктивність праці
Нехай функція
u
=
u
(
t
) виражає кількість виробленої продукції
u
за час
t
, і необхідно знайти продуктивність праці в момент
t
0
.
Очевидно, за період часу від
t
0
до
t
0
+
t'
кількість виробленої
продукції зміниться від значення
u
0
=
u
(
t
0
) до значення
u
+
u'
=
= u
(
t
0
+
t'
). Тоді середня продуктивність праці за цей термін
z
сер
=
u
t
'
'
.
Продуктивність праці в момент
t
0
можна визначити як граничне
значення середньої продуктивності за період часу від
t
0
до
t
0
+
t'
при
0t'o
, тобто
z =
0
lim
t'o
z
сер
=
0
lim
t
'o
u
t
'
'
=
0
()ut
c
.
Отже, похідна обсягу виробленої продукції за часом
0
()ut
c
є
продуктивність праці в момент
t
0
. У цьому економічний зміст по+
хідної.
У практиці економічних досліджень широке застосування отри+
мали виробничі функції, які використовують для встановлення за+
лежності, наприклад, випуску продукції від витрат ресурсів, витрат
виробництва від обсягу продукції, виторгу від проданого товару і т.д.
У припущенні диференційованості виробничих функцій важливе
значення набувають їхні диференціальні характеристики, пов’язані з
поняттям похідної.
Розглянемо похідні для означених типів виробничої функції.
1. Нехай виробнича функція
К = К
(
х
) — функція витрат вироб+
ництва, що залежить від кількості продукції
х
. Припустимо, що
кількість продукції збільшиться на
x
'
.
Кількості продукції
х +
x'
відповідають витрати виробництва
К'
=
К'
(
х +
x
'
)
– К
(
х
)
.
Середній приріст витрат виробництва є
К
x
'
'
. Це приріст витрат
виробництва на одиницю кількості продукції.
Граничними витратами виробництва
називається границя
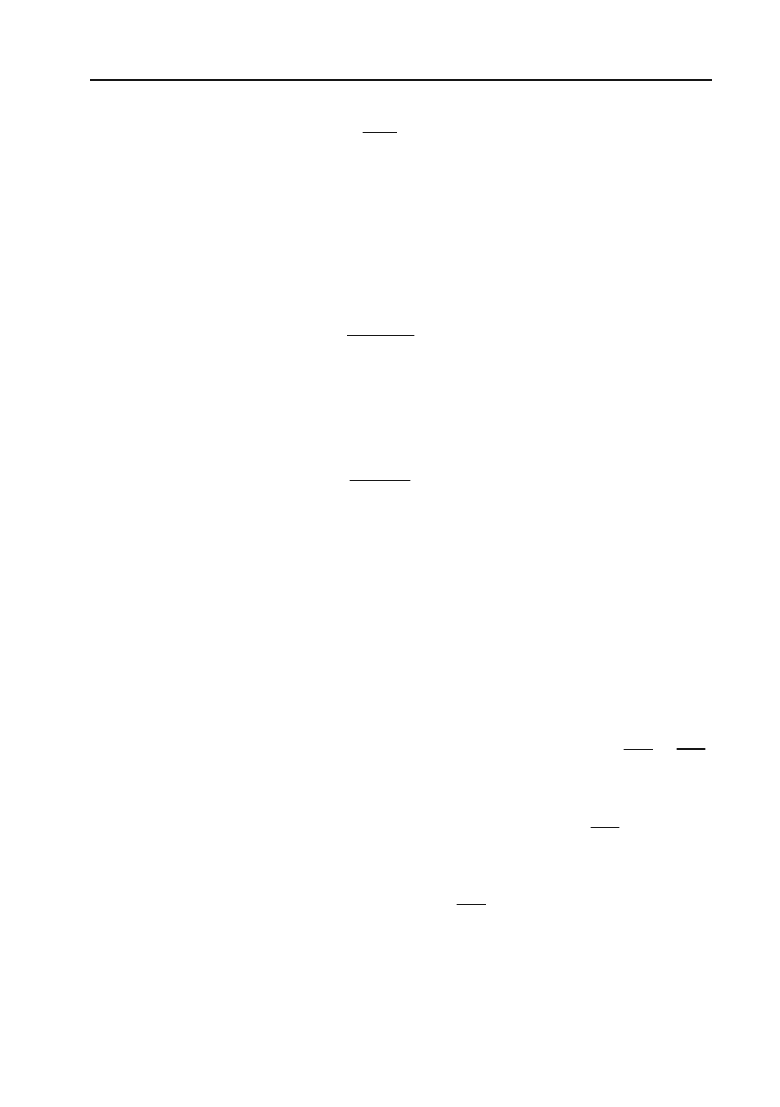
283
Розділ IV. Диференційне числення функції однієї змінної
0
lim
t
'o
К
x
'
'
=
()
Кx
c
.
Граничні витрати виробництва збігаються зі швидкістю зміни
витрат виробництва. Величина
()
Кx
c
характеризує наближено до+
даткові витрати на виробництво одиниці додаткової продукції.
2. Позначимо
U
(
x
) виторг від продажу
х
одиниць товару.
Граничним виторгом
називається границя
0
lim
t
'o
()Ux
x
'
'
=
()
Ux
c
.
3. Нехай виробнича функція
у = f
(
x
)
встановлює залежність ви+
пуску продукції
у
від витрат ресурсу
х
.
Граничним продуктом
називається границя
0
lim
t
'o
()fx
x
'
'
=
()
f
x
c
.
4.7.2. Еластичність
Нехай аргумент
х
функції
f
(
x
) одержав приріст
x
'
. Тоді значен+
ня функції зміняться на величину
y
'
=
f
(
x
+
x'
) –
f
(
x
).
Прирости
x'
і
y
'
називаються
абсолютними приростами аргумен
ту і функції
відповідно. Складемо відносні прирости змінних
x
x
'
і
y
y
'
.
Границя відношення відносного приросту функції
y
y
'
до відпо+
відного відносного приросту аргументу
x
x
'
при умові, що абсолют+
ний приріст аргументу
x
'
прямує до нуля, називається е
ластич
ністю функції
у = f
(
x
)
по змінній
х
і позначається символом
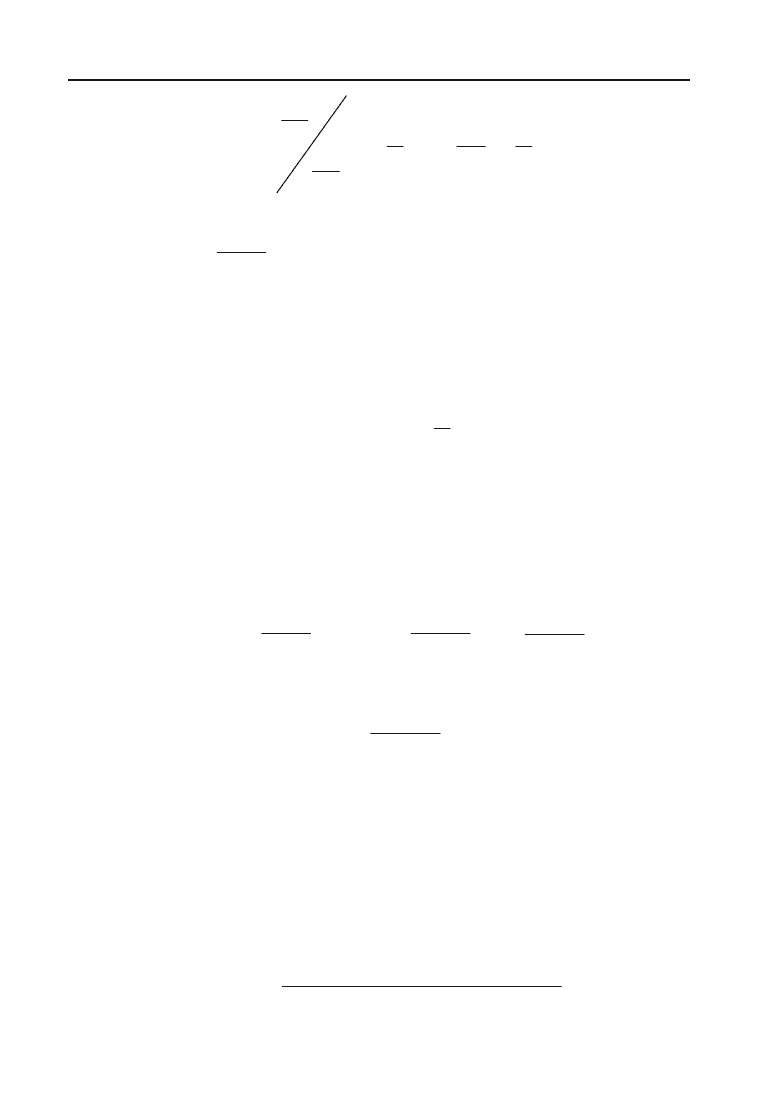
284
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Е
х
(
у
)
=
0
lim
t
'o
y
y
x
x
'
§·
¨¸
¨¸
'
¨¸
¨¸
©¹
=
x
y
0
lim
t'o
y
x
'
'
=
x
y
()
f
x
c
.
Е
х
(
у
)
=
()
x
f
x
()
f
x
c
.
(21)
Еластичність
Е
х
(
у
)
показує наближено, на скільки відсотків
зміниться значення функції
у = f
(
x
) у разі зміни незалежної змінної
х
на 1% (з
х
до
х +
0,01
х
).
Формулу (21) можна переписати у вигляді:
Е
х
(
у
)
=
()
f
x
c
:
y
x
.
Це означає, що для функцій випуску
у = f
(
x
) еластичність дорів+
нює відношенню граничного виробництва ресурсу до його середньо+
го значення виробництва.
Приклад 4.28.
Знайти
Е
х=2
(
f
(
x
)), якщо
f
(
x
)
=
3
х +
4
.
Розв’язок.
Еластичність заданої функції обчислюємо за формулою:
Е
х
(
f
(
x
))
=
()
x
f
x
()
f
x
c
=
34
x
x
3
=
3
34
x
x
.
Знайдемо
Е
х=2
(
f
(
x
)).
Е
х=2
(
f
(
x
)) =
32
32 4
=
0,6.
Це означає, що при збільшенні
х
з 2
до 2,02 значення функції
зростає на 0,6%.
1. Якщо |
Е
х
(
f
(
x
))|
<
1, то функція називається
нееластичною
(відносний її приріст спадає).
2. Якщо |
Е
х
(
f
(
x
))| >
1, то функція називається
еластичною
(віднос+
ний її приріст зростає).
Властивості:
1)
Е
х
(
f
(
x
)
r
g
(
x
))
=
() (()) () (())
() ()
xx
f
xE
f
x
g
xE
g
x
fx gx
r
r
;

285
Розділ IV. Диференційне числення функції однієї змінної
2)
Е
х
(
f
(
x
)
g
(
x
))
= Е
х
(
f
(
x
))
+ Е
х
(
g
(
x
));
3)
Е
х
(
f
(
x
)/
g
(
x
))
= Е
х
(
f
(
x
))
– Е
х
(
g
(
x
))
.
Еластичність елементарних функцій
1. Еластичність степеневої функції
у = х
n
стала і дорівнює показ+
нику степеня
n
:
Е
х
(
х
n
)
= n.
Справді:
Е
х
(
х
n
)
=
()
n
x
c
n
x
x
=
1
n
n
nx x
x
= n
.
2. Еластичність показникової функції
у = а
х
пропорційна до
х
.
Е
х
(
а
х
)
= х
ln
a.
Справді:
Е
х
(
а
х
)
=
()
x
x
a
c
x
x
a
=
ln
x
x
aax
a
= х
ln
a.
3. Еластичність лінійної функції
у = ах + b
Е
х
(
ах + b
)
=
ax
ax b
.
Справді:
Е
х
(
ах + b
)
=
()
ax b
c
x
ax b
=
ax
ax b
.
4.7.3. Використання еластичності в економічному аналізі
В економіці розглядають кілька видів еластичності.
І. Еластичність попиту відносно ціни.
Вивчається залежність попиту
d
на товар від ціни
р
на нього.
Залежність попиту від ціни опишемо за допомогою формули
d
=
d
(
р
).
В багатьох економічних дослідженнях необхідно встановити не
величину попиту при кожному конкретному рівні ціни, а характер
зміни попиту при вказаній зміні ціни. В такому випадку знаходять
еластичність попиту відносно ціни. В наших позначеннях:
Е
p
(
d
) =
()
p
dp
()
dp
c
.

286
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Еластичність попиту відносно ціни визначає, на скільки відсотків
зміниться попит на товар, якщо ціна на нього збільшиться на 1%.
Так як в більшості випадків попит являється спадною функцією ціни
р
і
()
dp
c
< 0, то щоб уникнути від’ємних чисел, в таких випадках
при вивченні еластичності попиту приймають
Е
p
(
d)
=
()
p
dp
()
dp
c
.
Знак «–» показує, що попит зменшується при збільшенні ціни.
Приклад 4.29.
Нехай функція попиту лінійна
d =
5
–
1
2
p,
то
Е
p
(
d
)
= –
1
5
2
p
p
1
2
§·
¨¸
©¹
=
10
p
p
.
Якщо
р =
2, то
Е
p
(
d
)
=
1
4
. Це означає, що при збільшенні ціни на
1% попит спадає на
1
4
%
.
Якщо
р
= 5, показник еластичності дорів+
нює 1. Збільшення ціни з 5 до 5,05 призводить до зменшення попиту
на 1%
.
Якщо
р =
9 попит зменшується на 9%
.
Вважають, що попит еластичний, якщо підвищення ціни на 1% відпо+
відає підвищенню попиту більш ніж на 1%, тобто
Е
p
(
d
) > 1, попит ней+
тральний, якщо
Е
p
(
d
)
=
1, попит нееластичний, якщо
Е
p
(
d
) < 1.
Іншими словами, попит на товар еластичний, якщо невелика зміна
ціни товару веде до значної зміни попиту на товар. Коли зміна ціни
веде до порівняно невеликої зміни величини попиту, попит являєть+
ся нееластичним.
Дослідимо динаміку виручки при різних видах попиту.
Виручка від продажу даного товару при ціні
р
складає
u = p
d
(
p
).
Гранична виручка дорівнює
du
dp
= d
(
p
)
+ p
()
dp
c
= d
(
p
)(1 +
()
p
dp
)
= d
(
p
)(1 –
Е
p
(
d
))
.

287
Розділ IV. Диференційне числення функції однієї змінної
а) Якщо попит еластичний, тобто
Е
p
(
d
) > 1, то
0
du
dp
, і з підви+
щенням ціни виручка від продажу товару понижається.
б) При нейтральному попиту
Е
p
(
d
)
=
1,
0
du
dp
, і виручка прак+
тично не залежить від ціни.
в) При нееластичному попиті (0
< Е
p
(
d
) < 1) виручка збільшуєть+
ся з ростом ціни, так як в цьому випадку
0
du
dp
!
.
Із розглянутого вище видно, що знання еластичності попиту на
даний товар дозволяє прогнозувати направлення зміни виручки під
впливом росту або зниження ціни. Очевидно, що кожній фірмі вигід+
но, щоб попит на її продукцію був як можна більш нееластичним,
так як в такій ситуації існує можливість призначення порівняно
високі ціни.
Еластичність пропозиції визначається аналогічно еластичності
попиту. Для диференційованої функції
S = S
(
p
) формула еластич+
ності приймає вигляд
Е
p
(
S
)
=
()
p
Sp
dS
dp
.
На відміну від формули еластичності попиту
у
формулі еластич+
ності пропозиції відсутній знак «–». Це пов’язано з тим, що з ростом
ринкової ціни на товар пропозиції на цій товар зростають. Кожному
підприємству вигідно реалізувати свою продукцію, через це
S = S
(
p
) —
зростаюча функція і
0
dS
dp
!
.
Пропозиція називається еластичною, якщо
Е
p
(
S
) > 1, нееластич+
ною, якщо 0
< Е
p
(
S
) < 1, і нейтральною, якщо
Е
p
(
S
) = 1.
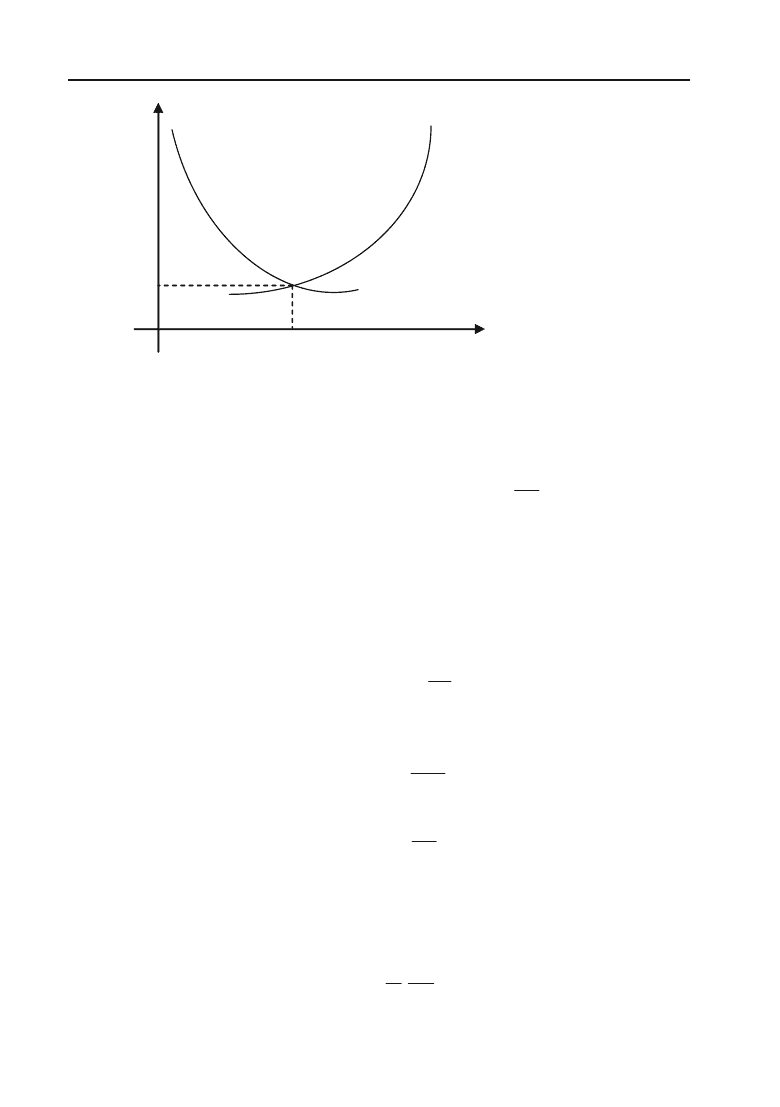
Ціна, при якій величина попиту дорівнює величині пропозиції,
називається ціною рівноваги.
В точці
М
величина попиту дорівнює величині пропозиції,
р
—
ціна рівноваги.
288
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
4.7.4. Розв’язання задач
Задача 4.30.
Нехай функція
К
(
х
) = 20
х
–
2
20
x
встановлює за+
лежність витрат виробництва від кількості
х
продукції, що випус+
кається. Знайти граничні витрати і коефіцієнт еластичності, якщо
обсяг продукції складає 100 одиниць, 20 одиниць.
Розв’язок.
1. Граничні витрати виробництва є похідна від функції витрат
()
Кx
c
= 20 –
10
x
.
При відповідних обсягах продукції:
(
100
)
К
c
= 20
–
100
10
= 10;
(20)
К
c
=
20
–
20
10
= 18.
Отже, чим більше виробляється продукції, тим повільніше рос+
туть витрати на її випуск.
2. Еластичність функції
Е
х
(
у
) =
x
y
dy
dx
.
0 p P
d(p)
d(S)
S(p) = d(p)
M
S =
S
(
p
)
d =
d
(
p
)
Рис. 4.3.

289
Розділ IV. Диференційне числення функції однієї змінної
У нашому випадку
у
(
х
) =
К
(
х
) = 20
х
–
2
20
x
;
Е
х
(
К
) =
2
20
20
x
x
x
(20 –
10
x
) =
2
(
200
)
400
x
x
;
Е
100
(
К
) =
2100
300
=
2
3
|
0,67;
Е
20
(
К
) =
2180
380
=
18
19
|
0,95.
Отже, якщо при обсязі випуску 100 одиниць кількість продукції,
що випускається, збільшиться на 1%, тобто на 1, то відносні витрати
виробництва збільшаться приблизно на 0,67%; при обсязі 20 одиниць
збільшення випуску продукції на 1% призведе до збільшення віднос+
них витрат приблизно на 0,95%.
Задача 4.31.
Залежність між витратами виробництва
у
і обсягом
продукції
х
, що випускається, виражається функцією
у =
50
х –
0,05
х
3
(грош. од). Визначити середні і граничні витрати, якщо обсяг про+
дукції 10 од.
Розв’язок.
Функція середніх витрат (на одиницю продукції) ви+
ражається відношенням
у
1
=
y
x
=
50 – 0,05
х
2
,
у
1
(10)
=
50 – 0,05
10
2
=
45
(грош. од.).
Граничні витрати:
y
c
=
50 – 0,05
3
х
2
;
(
10
)
y
c
=
35
(грош. од.).
Отже, якщо середні витрати на виробництво одиниці продукції
складають 45
грош. од., то граничні витрати, тобто додаткові витрати
на виробництво додаткової одиниці продукції при даному рівні ви+
робництва (обсязі продукції, що випускається у кількості 10
од.),
складають 35
грош. од.

290
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Задача 4.32.
Залежність між собівартістю одиниці продукції
у
(тис.
грош. од.) виражається функцією
у =
–0,5
x +
80
.
Знайти еластичність
собівартості, якщо випуск продукції дорівнює 60
млрд. грош. од.
Розв’язок.
Еластичність собівартості
Е
х
(
у
)
=
0,5 80
x
x
(–0,5)
=
160
x
x
,
Е
60
(
у
)
=
60
60 160
= –0,6.
Це означає, що у разі випуску продукції на 60 млрд. грош. од.
збільшення його на 1% призведе до зниження собівартості на 0,6%.
Задача 4.33.
Дослідним шляхом встановлено функції попиту
8
2
p
q
p
і пропозиції
S = p +
0,5, де
q, S
— кількість товару, що
купується і пропонується на продаж відповідно, в одиницю часу;
p
–
ціна товару. Знайти:
а) ціну рівноваги, тобто ціну, при якій попит і пропозиція врівно+
важуються;
б) еластичність попиту і пропозиції для цієї ціни;
в) зміну прибутку у разі збільшення ціни на 5%
від ціни рівно+
ваги.
Розв’язок.
а) Ціна рівноваги визначається з умови
q = S
:
8
2
p
p
= p +
0,5,
звідки
р =
2, тобто ціна рівноваги дорівнює 2 грош. од
.
б) Знайдемо еластичність попиту і пропозиції за формулою
Е
х
(
у
)
=
x
y
y
c
,
Тоді
q
c
=
2
6
(2)
p
;
S
c
=
1;
