Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

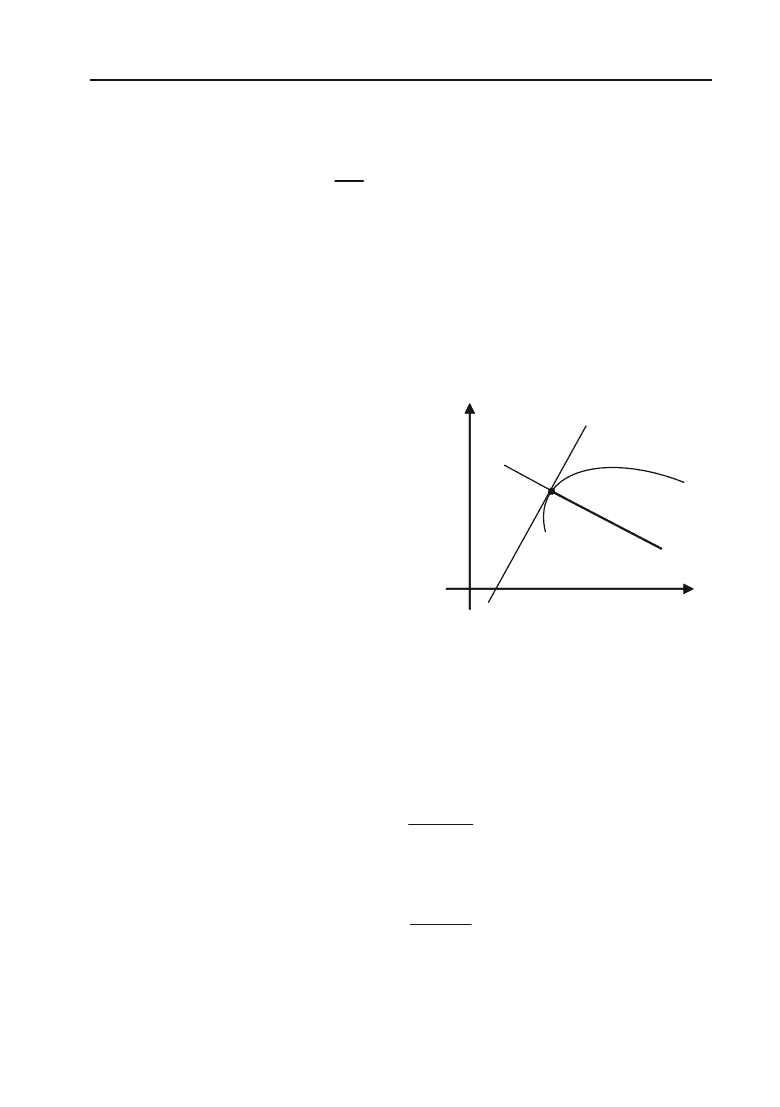
261
Розділ IV. Диференційне числення функції однієї змінної
до розглянутої кривої в даній точці з додатним напрямом осі
Ох
.
Отже, маємо:
0
lim
x'o
y
x
'
'
=
()
f
x
c
=
tg
D
.
Значення похідної в деякій точці дорівнює тангенсу кута, утворе+
ного дотичною до кривої в цій точці з додатним напрямком осі
Ох
—
в цьому заключається геометричний зміст похідної.
4.3.2. Дотична та нормаль до кривої
Розглянемо рівняння кривої
у
=
f
(
x
) (рис. 4.2).
Візьмемо на кривій точку
М
1
(
х
1
;
у
1
)
і складемо рівняння дотичної до цієї
кривої в точці
М
1
, припускаючи, що
дотична не паралельна жодній коор+
динатній осі. рівняння прямої, що
має кутовий коефіцієнт
k
і прохо+
дить через точку
М
1
має вигляд:
у
–
у
1
=
k
(
х
–
х
1
).
Для дотичної
1
()k
f
x
c
, тому
рівняння дотичної буде таке:
у
–
у
1
=
1
()
f
x
c
(
х
–
х
1
).
Нормаллю до кривої в даній точці називається пряма, яка прохо+
дить через цю точку і перпендикулярна до дотичної в ній.
Із означення нормалі випливає, що її кутовий коефіцієнт
k
нормалі
пов’язаний з кутовим коефіцієнтом
k
дотичної
рівністю:
k
нормалі
=
1
дотична
k
,
тобто
k
нормалі
=
1
1
()
f
x
c
.
Отже, дістаємо рівняння нормалі до кривої
у
=
f
(
x
) в точці
М
1
(
х
1
;
у
1
):
Y
X
0
y = f(x)
Нормаль
Дотична
М
1
(х
1
,у
1
)
Рис. 4.2.

262
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
у
–
у
1
=
1
1
()fx
c
(
х
–
х
1
).
Приклад 4.14.
Скласти рівняння дотичної та нормалі:
1) до параболи
у = х
2
–
4
х
в точці, де
х
1
= 1;
2) до кривої
у =
3
х
4
–
5
х
2
+
4
в точці
х
1
= –
1,
у
1
=
2;
3) до кривої 4
х
3
–
3
ху
2
+
6
х
2
–
5
ху –
8
у
2
+
9
х
+ 14
=
0
в точці
М
1
(–2; 3)
.
Розв’язок.
1) Підставимо в рівняння параболи задану абсцису точки дотику
х
1
= 1 і знайдемо її ординату:
у
1
=
1
2
– 4
1 = –3
.
Для визначення кутового коефіцієнту дотичної знайдемо по+
хідну
y
c
із рівняння параболи та обчислимо значення похідної в
точці
х
1
= 1.
2
(4)24yx x x
cc
,
(
1
)
y
c
= 21 – 4 = –2.
Підставляючи в рівняння дотичної
х
1
,
у
1
,
(
1
)
y
c
, одержуємо рівнян+
ня дотичної:
у
–(–3)
=
–2(
х
– 1)
або
2
х + у +
1 = 0,
і рівняння нормалі
у +
3
=
1
2
(
х –
1)
або
х –
2
у
– 7 = 0.
2) Перевіримо, чи задана точка
М
1
(–1; 2)
є точкою дотику:
3(–1)
4
– 5(–1)
2
+ 4 = 3 – 5 + 4 = 2
Знаходимо кутовий коефіцієнт дотичної:
y
c
=
12
х
3
–
10
х
,
k =
(1)
y
c
=
12(–1)
3
– 10(–1) = –12 + 10 = –2.

263
Розділ IV. Диференційне числення функції однієї змінної
Рівняння дотичної:
у –
2 = –2(
х +
1),
2
х + у =
0.
Рівняння нормалі:
у –
2
=
1
2
(
х
+ 1),
2
у
– 4
= х
+ 1,
х
– 2
у
+ 5 = 0.
3) Перевіривши, що задана точка
М
1
(–2; 3) лежить на кривій,
тобто є точкою дотику, знаходимо кутовий коефіцієнт дотичної.
Рівняння кривої задане в непевному виді. Знаходимо похідну за
правилом диференціювання непевної функції.
12
х
2
– 3
у
2
– 6
ху
y
c
+
12
х –
5
у –
5
х
y
c
–
16
у
y
c
+
9 = 0,
6
ху
y
c
+ 5
х
y
c
+
16
у
y
c
=
12
х
2
–
3
у
2
+
12
х –
5
у
+ 9,
22
12 3 1259
6516
xy xy
y
xy x y
c
,
22
12( 2) 3(3) 12( 2) 5 3 9
(2;3)
6( 2)3 5( 2) 16 3
y
c
=
9
2
.
Рівняння дотичної:
у –
3
=
9
2
(
х
+2),
2
у
– 6
=
–9
х
– 18,
9
х +
2
у +
12 = 0.
Рівняння нормалі:
у
– 3 =
2
9
(
х +
2),
9
у
– 27 = 2
х
+ 4,
2
х –
9
у
+ 31 = 0.
264
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Приклад 4.15.
Знайти рівняння дотичної та нормалі до кривої:
2cos 3sin ;
cos 3sin .
x
tt
y
tt
®
¯
в точці, де
2
t
S
.
Для того щоб скористатися формулами рівнянь дотичної та нор+
малі, необхідно визначити
х
1
,
у
1
,
()
y
t
c
,
при
2
t
S
.
Спочатку визна+
чимо
х
1
і
у
1
:
х
1
= 2cos
2
S
+ 3sin
2
S
= 3,
y
1
= cos
2
S
+ 2sin
2
S
= 2.
Після цього знаходимо
x
y
c
похідну в точці
t =
2
S
.
x
y
c
=
t
t
y
x
c
c
=
(cos 2sin )
(2cos 3sin )
t
t
tt
tt
c
c
=
sin 2cos
2sin 3cos
tt
tt
,
x
y
c
(
t =
2
S
)
=
sin 2cos
22
2sin 3cos
22
SS
SS
=
1
2
=
1
2
.
Рівняння дотичної:
у –
2
=
1
2
(
х
– 3),
2
у
– 4
= х
– 3,
х
– 2
у
+ 1 = 0.
Рівняння нормалі:
у
– 2
=
2(
х
– 3),
у
– 2
=
–2
х +
6,
2
х + у
– 8 = 0.

265
Розділ IV. Диференційне числення функції однієї змінної
4.3.3. Задачі для самостійного розв’язку
Задача 4.16.
Знайти рівняння дотичних і нормалей до заданих
кривих в указаних точках і побудувати криві, дотичні та нормалі:
а) до параболи
у
= 4 –
х
2
в точці, де
х
1
= –1;
б) до гіперболи
у
2
– 2
х
2
= 1 в точках, де
х
1
= 2;
в) до еліпса
2 3 cos
2sin
xt
y
t
°
®
°
¯
в точці, де
t
=
6
S
.
Задача 4.17.
На колі
х
2
+
у
2
= 25 знайти точки дотику, де дотич+
на паралельна прямій 3
х
+ 4
у
– 12 = 0. скласти рівняння дотичних.
Побудувати коло, пряму та дотичні.

266
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§4.4. Диференціал функції. Застосування диференціала для
наближених обчислень
4.4.1. Диференціал функції
Із визначення похідної
()
f
x
c
=
0
lim
x'o
y
x
'
'
та границі змінної
слідує, що
y
x
'
'
=
()fx
D
c
або
()
yf
xx x
D
c
' ''
, де
0
D
o
,
якщо
0
x
'o
, тобто приріст функції може бути представлений в
вигляді суми двох доданків. Перший доданок
()
f
xx
c
'
містить
приріст
x'
незалежної змінної в першому степені, тобто він лінійний
відносно
x'
. Цей перший доданок є головною частиною приросту
функції.
Головна частина приросту функції
y
, лінійна відносно приросту
незалежної змінної, називається
диференціалом функції
і позна+
чається знаком
dy:
()d
yf
xx
c
'
.
Диференціал незалежної змінної
х
дорівнює її приросту
d
y
x '
.
Через це
()d
yf
xdx
c
,
тобто диференціал функції дорівнює її похідній, помноженій на ди+
ференціал незалежної змінної. Отже, щоб знайти диференціал якої+
небудь функції, необхідно знайти похідну цієї функції і помножити
її на диференціал незалежної змінної.
4.4.2. Обчислення основних диференціалів
Таблиця для обчислення диференціалів основних елементарних
функції одержується із таблиці похідних цих функцій шляхом помно+
ження відповідної похідної на диференціал незалежної змінної
dx
.
Правила обчислення диференціалів:
1.
d
(
Cu
) =
Cdu
, де
C
= const.

267
Розділ IV. Диференційне числення функції однієї змінної
4.4.3. Інваріантність форми першого диференціала функції
Нехай
у
=
f
(
u
), де
u
є незалежною змінною, тоді диференціал цієї
функції запишеться у вигляді
dy
=
()
f
u
c
du
.
Якщо
у
=
f
(
u
), де
()
ux
M
, тоді функція
у
=
f
(
u
) буде складе+
ною функцією від змінної
х
. Обчислимо диференціал цієї функції:
(()) (()) () () ()
d
yf
xdx
f
xxdx
f
uudx
f
udu
MMM
cc c ccc
.
Отже, ми повернулися до вигляду диференціала, який був запи+
саний за припущенням, що змінна u є незалежною. Маємо властивість
диференціала, яка називається інваріантністю.
2.
d
(
u
r
v
) =
du
r
dv
.
3.
d
(
u
v
) =
udv
+
vdu
.
4.
u
d
v
§·
¨¸
©¹
=
2
vdu udv
v
.
4.4.4. Застосування диференціала для наближених значень
Відомо, що
y
'
=
f
(
x
+
x
'
) –
f
(
x
).
Якщо
()
yf
xx
c
'| '
,
то
f
(
x +
x'
)
|
f
(
x
)
+
()
f
xx
c
'
.
Одержана формула дозволяє за відомими значеннями функції і її
похідної в точці
х
знайти наближене значення функції в точці
x +
x'
,
що близька до
х
, і тим самим дає можливість використовувати дифе+
ренціал функції для находження наближених значень.
4.4.5. Економічне застосування диференціала. Мультиплікатор
Розглянемо найпростішу модель, яка описує динаміку зростання
прибутку залежно від інвестицій
Y
=
C
+
, де
Y
— прибуток,
C
—
споживання,
— інвестиції. Нехай
()
YY
,
()
CC
. Як впли+
ває зміна інвестицій
dI
на прибуток?
268
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
4.4.6. Розв’язання прикладів
Приклад 4.18.
Знайти диференціал функції
у
=
х
3
– 3
х
.
Розв’язок.
Знаходимо похідну даної функції і, помноживши на ди+
ференціал незалежної змінної, одержуємо диференціал даної функції.
dy
=
y
c
dx
=
3
(3)
x
x
dx
c
= (3
x
2
– 3
x
ln3)
dx
.
Нехай
()dY Y dI
c
. Із рівняння
(())
YCY
— знайдемо
залежність між інвестиціями і швидкістю зростання прибутку:
() ()1
dC
YY
dY
cc
,
тобто
dY
=
1
1
dC
dY
,
або у диференціалах
dY
=
1
1
d
C
c
=
d
P
.
Вираз
1
1 C
P
c
називається
мультиплікатором
.
Мультиплікатор
— це числовий коефіцієнт, який показує у
скільки разів сума приросту або скорочення прибутку перевищує
початкову суму інвестицій.
Термін уперше був уведений в 1931 р. Ф.Каюмом і набув подаль+
шого розвитку в кейнсіанській моделі визначення рівня рівноваги
прибутку.
У розглянутій моделі маємо: якщо 0 <
dC
dY
=
()
CY
c
< 1, то
P
> 1.
Отже, додаткові інвестиції посилюватимуть прибуток.

269
Розділ IV. Диференційне числення функції однієї змінної
Приклад 4.19.
Обчислити наближено arctg 0,98.
Розв’язок.
Якщо необхідно обчислити
f
(
x
1
) і якщо простіше об+
числити
f
(
x
0
) і
0
()
f
x
c
, то при достатньо малій по абсолютному зна+
ченню різниці
х
1
–
х
0
=
x'
можна замінити приріст функції її дифе+
ренціалом
10 0
() () ()
f
x
f
x
f
xx
c
|'
.
Нехай arctg 0,98 є значення функції
у
= arctg
x
при
х
1
= 0,98.
Нехай
х
0
= 1, тоді
f
(
x
0
) = arctg 1 =
4
S
;
2
1
1
y
x
c
.
0
()
f
x
c
=
(
1
)
f
c
=
2
1
11
=
1
2
,
x
'
=
х
1
–
х
0
= 0,98 – 1 = –0,02.
Користуючись формулою
10 0
() () ()
f
x
f
x
f
xx
c
|'
, одержуємо:
arctg 0,98
|
4
S
+
1
2
(–0,02)
|
0,7754.
4.4.7. Приклади для самостійного розв’язку
Приклад 4.20.
Знайти диференціали функцій
1)
y
= 5
ln tg x
;
2)
y
=
arcsin
x
+ (arctg
x
)
2
;
3)
y
=
1
2
3
x
+ 3
x
2
– 4
x
;
4)
y
= ln(1 +
e
10x
) + arсctg
e
5x
, обчислити
0x
dy
c
,
dx
= 0,1.
Приклад 4.21.
Знайти наближене значення
а) ln 1,01;
б)
5
31
.

270
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
§4.5. Привило Лопіталя та застосування його
до знаходження границь функцій
Раніше були пояснені елементарні способи знаходження границь
функції в тих випадках, коли аргумент необмежено зростає або пря+
мує до значення, які не входять в область визначення функції. Крім
цих елементарних способів, ефективним засобом для знаходження
границі функції в указаних особливих випадках являється наступне
правило Лопіталя: границя відношення двох нескінченно малих або
двох нескінченно великих величин дорівнює границі відношення їх
похідних (якщо остання границя існує або дорівнює нескінченості).
4.5.1. Випадки
0
0
½
®¾
¯¿
та
f
½
®¾
f
¯¿
Випадки знаходження границь:
1)
0
0
½
®¾
¯¿
— коли функція являє відношення двох нескінченно ма+
лих величин;
2)
f
½
®¾
f
¯¿
— коли функція являє відношення двох нескінченно ве+
ликих величин.
Згідно правилу Лопіталя в цих випадках можна замінити відно+
шення функцій відношенням їх похідних, тобто якщо
1
()
x
M
та
2
()
x
M
одночасно прямують до нуля або до нескінченості при
x
ao
або
x
of
, то
1
2
()
lim
()
x
x
M
M
=
1
2
()
lim
()
x
x
M
M
c
c
.
Якщо остання границя існує або дорівнює нескінченості, то вона
буде дорівнювати шуканій границі. Якщо ж відношення похідних
