Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

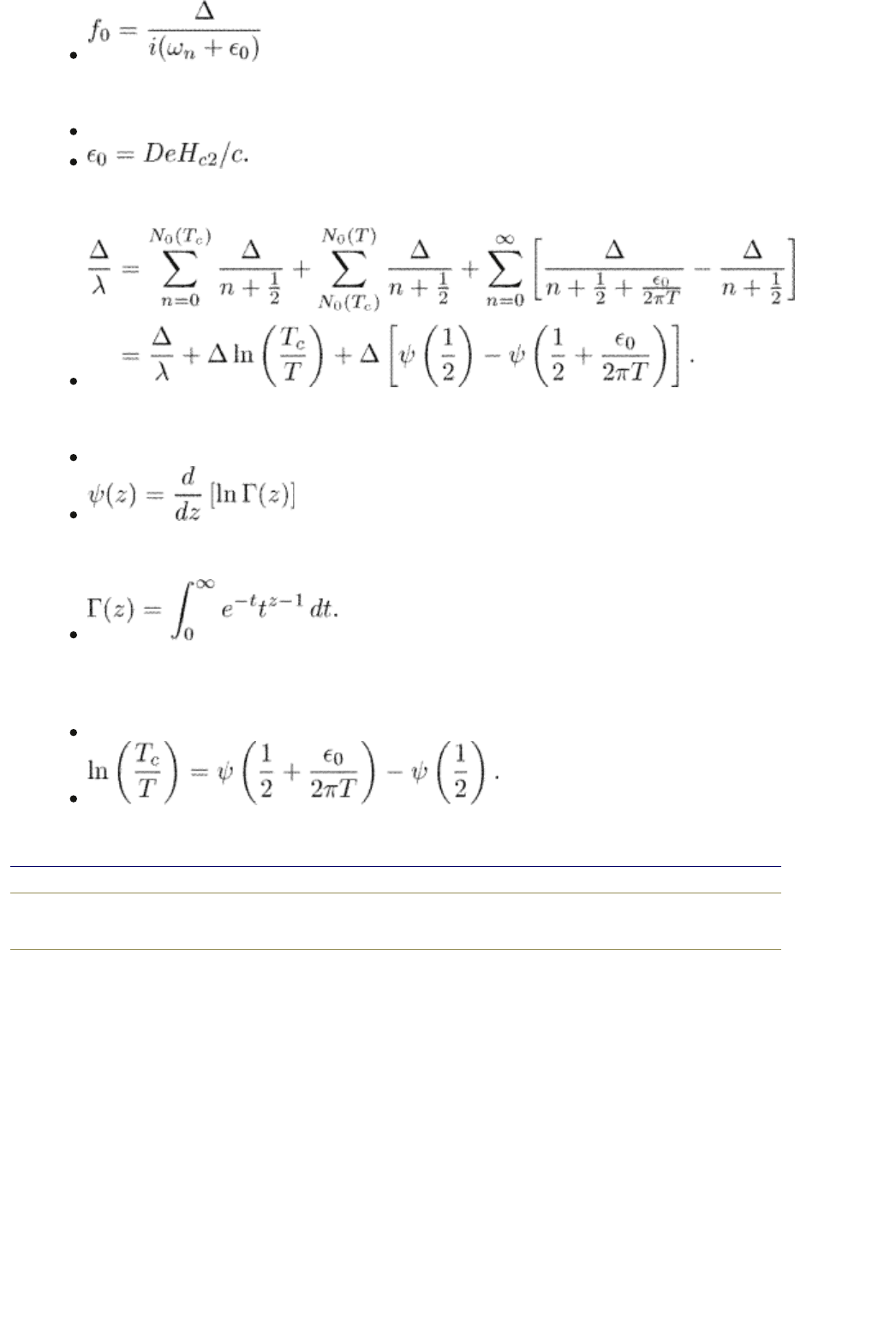
where

(6.36)

Using the expression for T

we can write the order parameter equation as

Here

(6.37)

is the so-called digamma function coupled to the Euler gamma function

Finally, we obtain the equation which determines the upper critical magnetic field

(Maki 1969)

(6.38)

end p.108

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共7页 2010-8-8 15:28

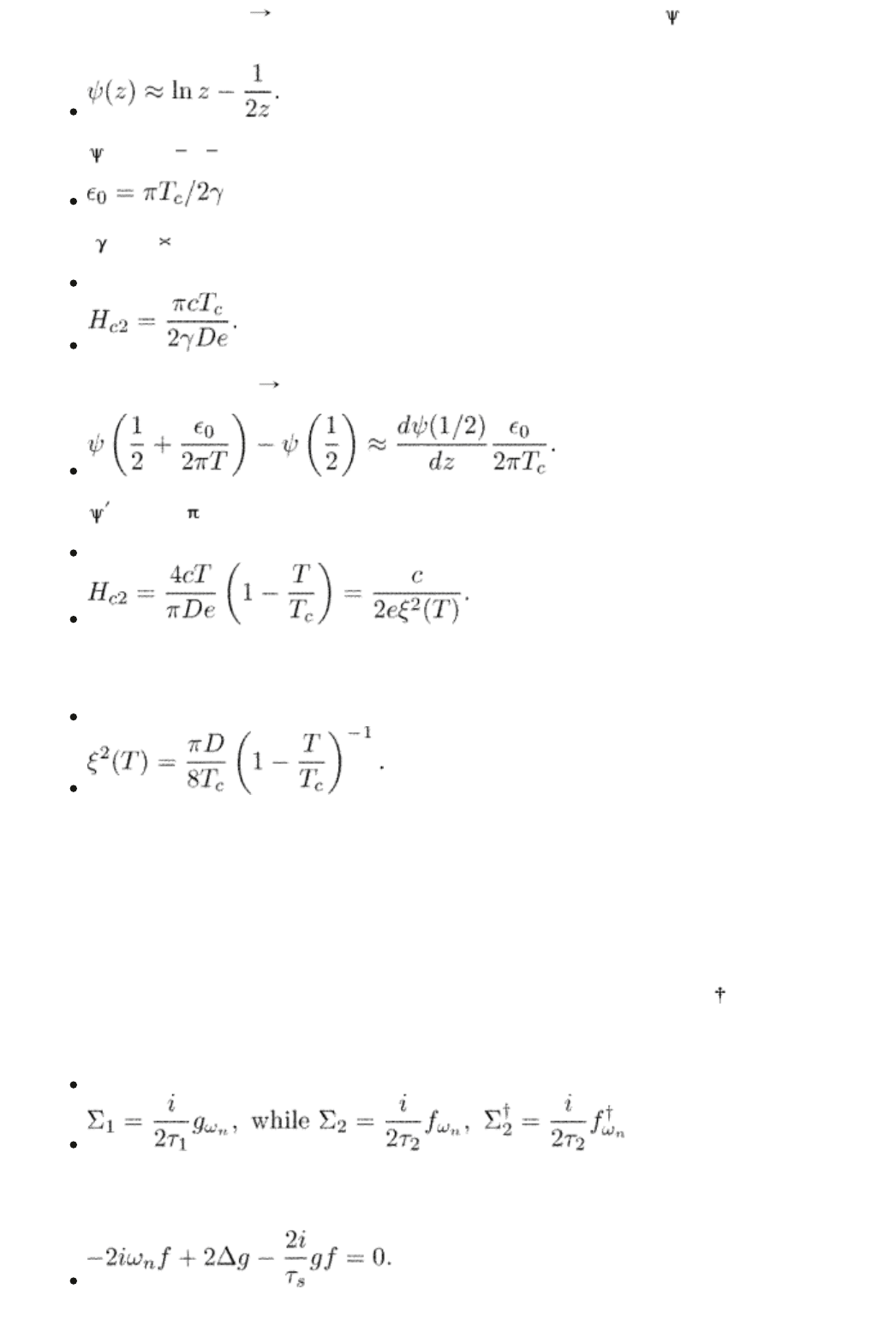
For low temperatures, T 0, we can use the asymptotic expression for (z) for

large z:

Since (1/2) = C 2 ln 2 we obtain

where = e

1.78. Equation (6.36) gives the upper critical field

(6.39)

For high temperatures, T T

, we have

Since (1/2) =

/2, we obtain

(6.40)

This result coincides, of course, with the solution of the Ginzburg–Landau

equation (1.34) since the coherence length in the dirty limit is

(6.41)

6.2 Gapless s-wave superconductivity

Consider an alloy with magnetic impurities (Abrikosov and Gor’kov 1960).

Scattering on an impurity atom depends on the spin state of an electron. The

scattering process breaks the spin coherence of paired electrons and leads to a

suppression of superconductivity. The key point is that the self-energies for g and

f contain different scattering times since the functions g, on one hand, and f, f

on the other hand, have different spin structures, For a homogeneous case we

have from eqns (5.74) and (5.75)

(6.42)

where the mean free times are defined by eqns (4.16) and (4.17). The

Eilenberger equation (5.84) gives

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共7页 2010-8-8 15:28

where the spin-flip time is determined by eqn (4.18). Therefore,

end p.109

(6.43)

From the normalization condition g

= 1 we find

(6.44)

and

(6.45)

6.2.1 Critical temperature

The order parameter equation (5.27) takes the form

(6.46)

Let us find the critical temperature. Putting = 0, we get g = 1 and

(6.47)

Here T

is the critical temperature without magnetic impurities, eqn (3.83):

We obtain

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共7页 2010-8-8 15:28

(6.48)

It is the familiar equation: we have seen it on page 108 when we calculated the

upper critical field for a dirty superconductor.

end p.110

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第7页共7页 2010-8-8 15:28

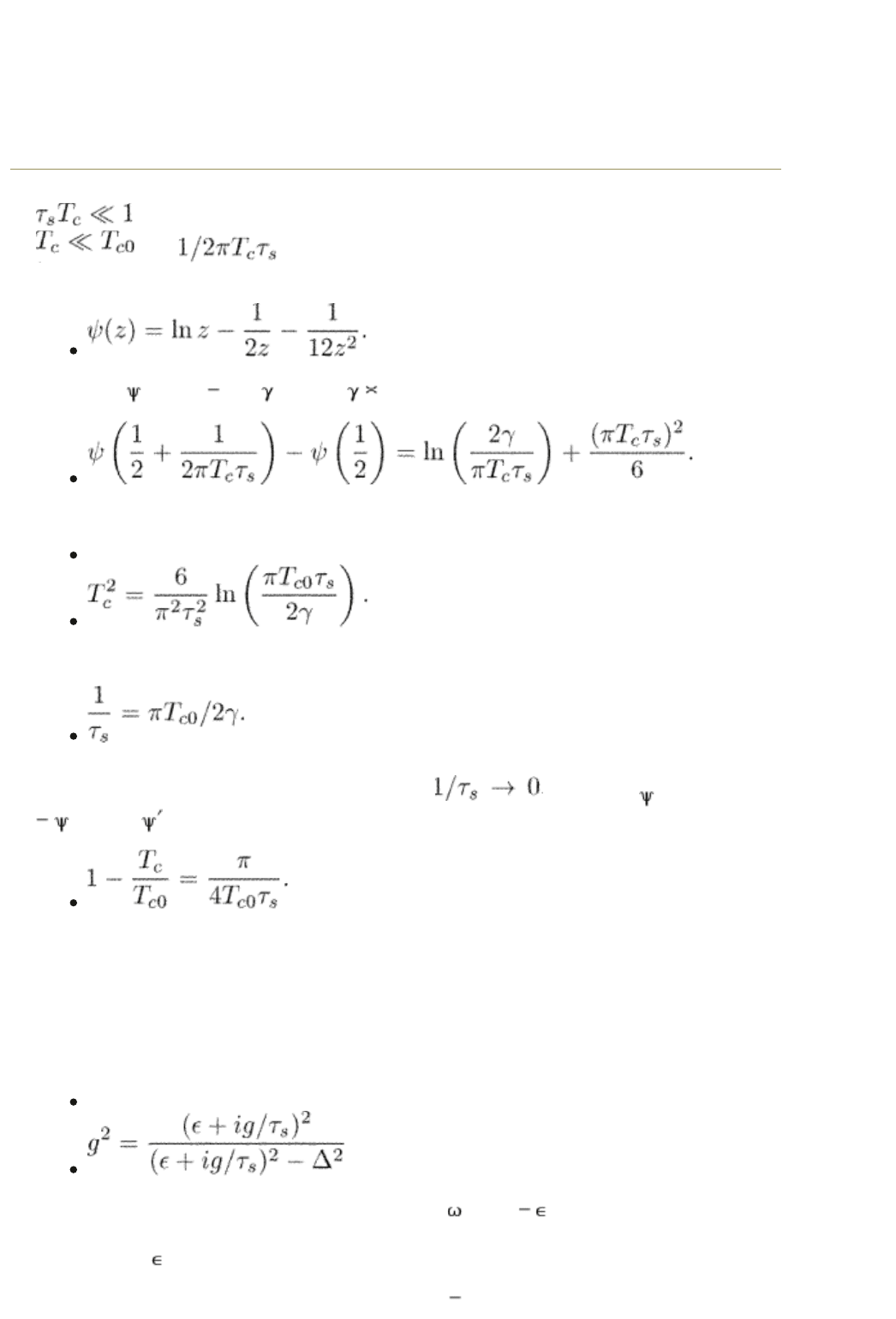
Let us consider a limiting case when the spin-flip scattering rate is large:

. In this limit, the critical temperature decreases down to zero,

and increases. For large arguments, we can use the

asymptotics

The value (l/2) = ln(4 ) where 1.78. We have

As the result, the critical temperature is

(6.49)

The critical temperature vanishes when the scattering rate is

For low concentration of magnetic impurities, , we have (1/2 + x)

(1/2) = (l/2)x and

The critical temperature is slightly reduced from its value without magnetic

impurities.

6.2.2 Gap in the energy spectrum

The real-frequency (retarded and advanced) Green functions are found from

(6.50)

which is obtained from eqn (6.44) by replacing

with i . Retarded function g

is defined as the solution of eqn (6.50) which has no singularities in the upper

half-plane of

, while g

should not have singularities in the lower half-plane.

Let us look for a solution in the form g

= g

= ia where a is a real function. If

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [111]-[115]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共6页 2010-8-8 15:29

such a solution exists for a given energy , the density of states g

= 0. This

means that the corresponding energy is below the energy gap. We have for a

(6.51)

This gives

(6.52)

end p.111

We choose the solution with the + sign since it gives the correct behavior in the

case without magnetic impurities

. Indeed, without magnetic

impurities we would have

for | | < . It results in the asymptotics a + for / 1 0 which should

be reproduced by eqn (6.52). Equation (6.52) for

takes the form

where we define the function

(6.53)

For , the function F(a) has a positive maximum. Calculating the

derivative we find that the maximum is reached at

The function at maximum is equal to

Therefore, a real solution for a exists if < F

maz

. Thus

is the gap in the energy spectrum. For >

, there is no real solution for ,

thus g becomes complex: g

= ia + b and g

= ia b with a finite density of

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共6页 2010-8-8 15:29

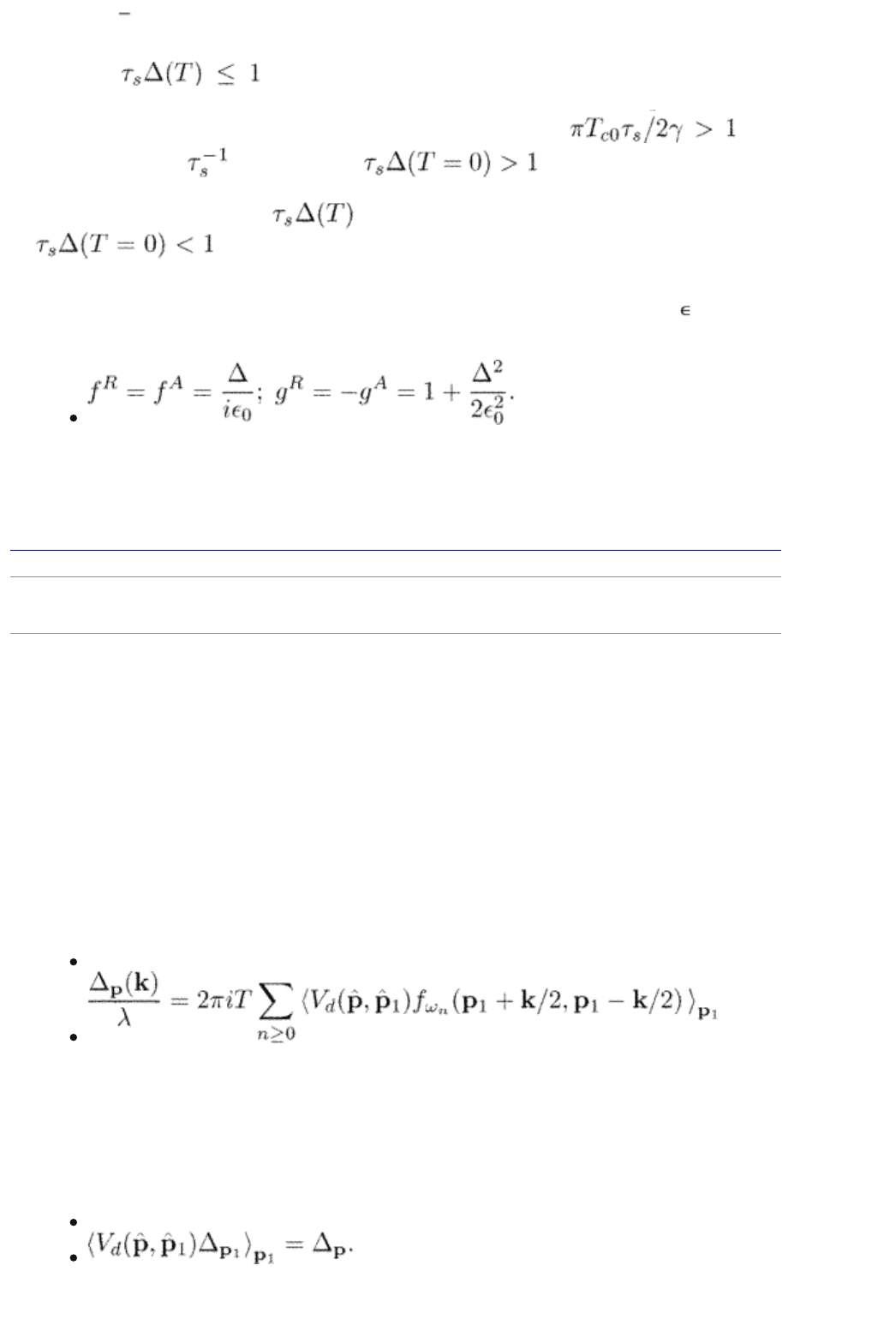
states g

= 2b.

The energy gap disappears when the order parameter satisfies the gapless

condition

. Note that there is a temperature range where

superconductivity exists without an energy gap in the excitation spectrum.

Indeed, superconductivity exists for temperatures below T

. For low enough , the condition is obviously fulfilled,

and there is an energy gap for low temperatures. However, the gap vanishes at

higher temperatures when

decreases down to 1. In the opposite case,

, the energy gap is absent for all temperatures.

We note that the vicinity of the upper critical field considered in the previous

section also belongs to the gapless regime. Indeed, for the real frequency

= 0

one has from eqn (6.35)

The density of states is thus finite. The gapless situation can be created also by

an inelastic electron–phonon scattering within certain range of temperatures (see

Section 11.2).

end p.112

6.3 Aspects of d-wave superconductivity

Many problems of d-wave superconductivity can be successfully solved using the

quasiclassical methods. Their applications for stationary and nonequilibrium

properties of d-wave superconductors can be found in many publications (see, for

example. Graf et al. 1995, Graf et al. 1996); they belong to a rapidly growing

field of research. We consider in this section only several selected examples.

6.3.1 Impurities and d-wave superconductivity

The order parameter of a d-wave superconductor satisfies the self-consistency

equation (5.29). It has the form

(6.54)

in the quasiclassical approximation. Here we average over the directions of p

the Fermi surface according to eqn (5.73) having in mind that the Fermi surface

can be nonspherical. For example, in d-wave superconductors which have

uniaxial crystal symmetry, its shape is more close to a cylinder. The d-wave

pairing potential has the structure of eqn (3.53). It is normalized in such a way

that

(6.55)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共6页 2010-8-8 15:29

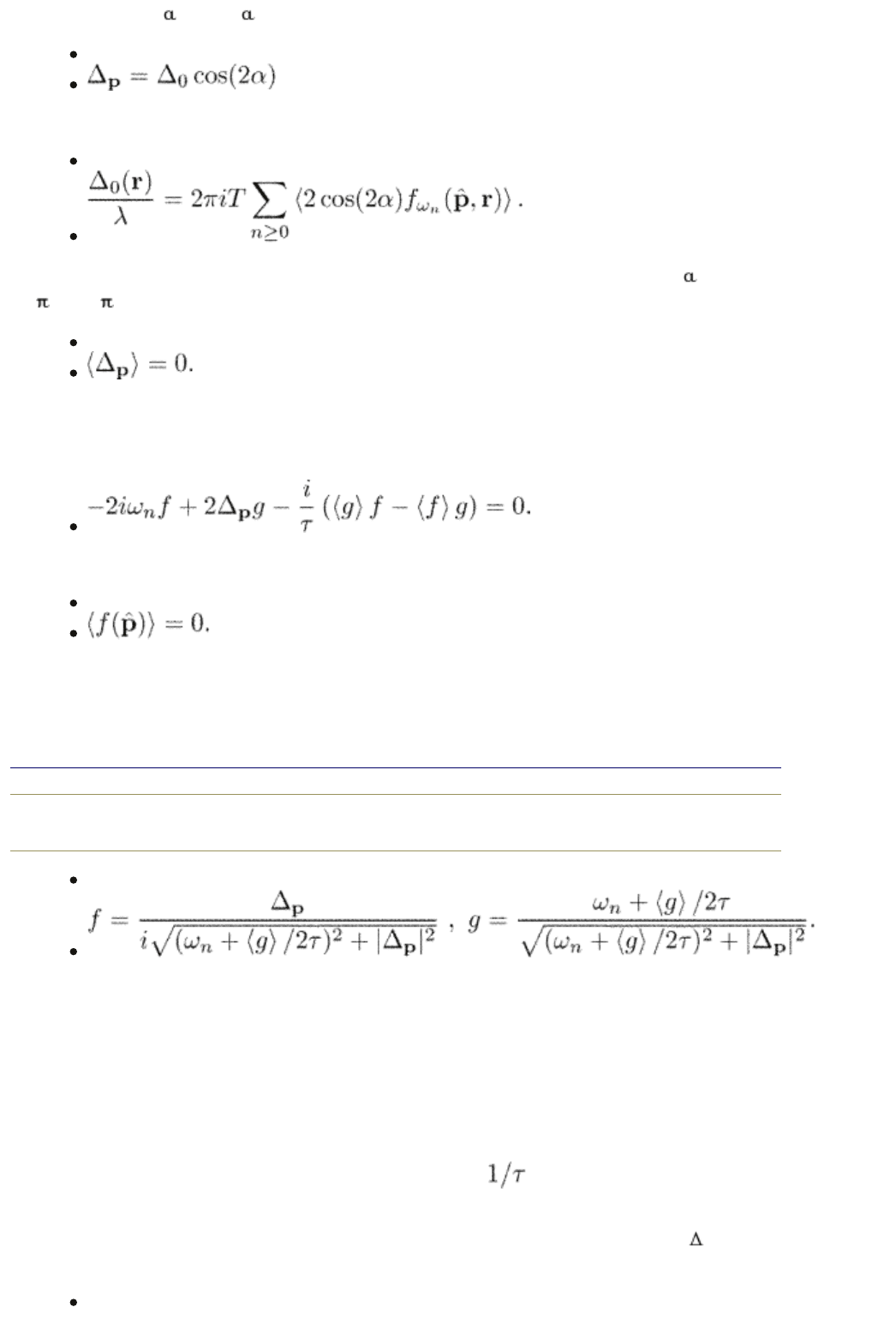
If V

= 2 cos(2 ) cos(2

) the order parameter in a d-wave superconductor is

(6.56)

where the amplitude satisfies the equation

(6.57)

The order parameter has nodes, i.e., it vanishes for momentum directions =

/4 + ( /2)n. Note that

(6.58)

We restrict ourselves to a homogeneous case. The quasiclassical Green functions

are found from the Eilenberger equations. We assume an isotropic scattering by

impurities. We have from eqn (5.84)

As we shall see later, in a homogeneous state,

(6.59)

Under this condition, the self-energies do not drop out of the Eilenberger

equation eqns (5.83) – (5.85) any more. Instead, we obtain with help of the

normalization condition g

– f

= 1

end p.113

(6.60)

With this solution, it easy to see that eqn (6.59) holds.

Equation (6.60) resembles the expressions for an alloy with magnetic impurities.

Indeed, properties of a d-wave superconductor with usual nonmagnetic impurities

are very much similar to those for magnetic s-wave alloys. First of all, the

presence of impurities suppresses the d-wave superconductivity. The reason is

that the scattering by impurities destroys the momentum coherence of the paired

state in a way similar to that by which the spin-dependent scattering destroys

the spin coherence of the paired state in an s-wave superconductor. We thus can

anticipate that there exists a critical scattering rate

such that the critical

temperature of the d-wave superconductor vanishes.

To find the critical temperature as a function of the scattering rate, we put

= 0

in eqn (6.60) and insert thus obtained f into eqn (6.57). We have

(6.61)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共6页 2010-8-8 15:29

This is exactly the equation (6.47) for the critical temperature of a magnetic

alloy with the substitution

. Therefore, we obtain

(6.62)

Here T

is the critical temperature without impurities

The critical temperature vanishes for

This shows that d-wave superconductivity can exists only in rather clean

compounds.

6.3.2 Impurity-induced gapless excitations

Presence of impurities broadens the order parameter nodes into gapless

low-energy states (Gor’kov and Kalugin 1985). In a strict sense, there is no

energy gap in a d-wave alloy. To see that, let us find the real-frequency Green

function. The retarded function is from eqn (6.60)

(6.63)

Let us find the average

end p.114

We have for = 0

(6.64)

We shall see that therefore, the angles with a small

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共6页 2010-8-8 15:29

cos(2 ) are important. We put x = /4 . Substituting cos(2 ) 2x for small

x, we get

(6.65)

since there are 4 nodes. Calculating the integral we find

(6.66)

The averaged Green function is

(6.67)

It is a real quantity. Thus there exists a finite density of states at zero energy

It is exponentially small in the clean limit in the Born approximation.

However, the density of states becomes a power-law function if the impurity

scattering is strong such that it should be treated within the full scattering

amplitude (Graf et al. 1996).

We see that there is no energy gap: a small but finite density of states exists

down to zero energy. The angle-resolved density of states for

= 0 is

where

One can say that, instead of gap nodes, there opens “an impurity band” with the

bandwidth 2

6.3.3 The Ginzburg–Landau equations

Here we consider an ideal case where the pairing potential has only a d-wave

component. A more complete version of the Ginzburg–Landau equation including

both d-wave and s-wave components of the pairing potential and the order

end p.115

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共6页 2010-8-8 15:29