Крупкина Т.В. Математическая статистика

Подождите немного. Документ загружается.

α = 0, 05.

∗

= χ

l−r−1; 0,95

= χ

3−0−1; 0,95

= χ

2; 0,95

= 5, 99

(последнее значение нашли по таблице).

< t

∗

следовательно, гипотезу H

не отвергают.I

16.4. Проверка гипотезы однородности: критерий Колмогорова –

Смирнова

Теорема 16.3 (теорема Смирнова). Пусть F

(x) и F

(x) – две эмпири-

ческие функции, построенные на основе двух независимых выборок

объемов n и m из одного и того же распределения F

, и

n,m

= sup

−∞<x<∞

(x) − F

(x)|. (122)

Тогда если теоретическая функция F (x) непрерывна, то для любого

фиксированного t > 0

lim

n,m→∞

P (|

nm/(n + m)D

n,m

6 t| = K(t), (123)

где функция K(t) определена равенством (116).

Эта теорема позволяет ответить на важный практический вопрос,

можно ли считать, что две выборки получены из одного и того же распреде-

ления.

Есть две выборки X = (X

, . . . , X

) и Y = (Y

, . . . , Y

), причем

∈ F

, Y

∈ F

, и распределения F

, F

, вообще говоря, неизвестны. Про-

веряется сложная гипотеза H

: F

= F

против альтернативы H

: F

6= F

Если F

, F

имеют непрерывные функции распределения, применим

критерий Колмогорова – Смирнова.

Пусть F

n,x

и F

m,y

– эмпирические функции распределения, построен-

ные по выборкам X и Y ,

Z(X, Y ) =

n + m

max

n,x

(t) − F

m,y

(t)|.

Если гипотеза H

верна, то Z(X, Y ) ⇒ ξ ∈ K (распределение, имею-

щее функцию распределения Колмогорова) при n, m → ∞.

151

Замечание 16.2. Если верна гипотеза H

, то Z(X, Y )

−→ ∞ при

n, m → ∞.

Если случайная величина ξ имеет функцию распределения K(y), то

по заданному α найдем C такое, что α = P(ξ > C). Построен критерий

согласия Колмогорова – Смирнова:



, Z(X, Y ) < C;

, Z(X, Y ) > C.

Если число выборок больше двух, то для проверки гипотезы однород-

ности можно пользоваться одним из вариантов критерия χ

Пирсона

16.5. Проверка гипотезы независимости: критерий χ

Пирсона

Не волнуйся, голова!

Теперь будет думать компьютер.

Гомер Симпсон

По выборке (X, Y ) = ((X

, Y

), . . . , (X

, Y

)) значений двух наблюда-

емых совместно величин ξ и η в n экспериментах будем проверять гипотезу

: ξ и η независимы.

Сгруппируем значения ξ в k интервалов, а значения η в m интерва-

лов и подсчитаем эмпирические частоты для каждого интервала двумерной

группировки (i = 1, . . . , k, j = 1, . . . , m).

(Здесь µ

i,j

– число пар (X, Y ), попавших в клетку δ

× δ

, и т. д.)

Y δ

. . . δ

1,1

1,2

. . . µ

1,m

2,1

2,2

. . . µ

2,m

. . . .

k,1

k,2

. . . µ

k,m

Σ a

. . . a

Если гипотеза H

верна, то теоретические вероятности попадания па-

ры (X

, Y

) в любую из областей δ

×δ

равны произведению вероятностей:

i,j

= P((X

, Y

) ∈ δ

× δ

) = P(X

∈ δ

)P(Y

∈ δ

) = p

Критерий Пирсона применяется для проверки разных гипотез – согласия, однородности, независимости.

152

и по ЗБЧ частоты должны быть близки к вероятностям:

≈ p

i,j

≈ p

i,j

Статистикой критерия служит функция, учитывающая различия меж-

ду µ

i,j

Z(X, Y ) = n

i=1

j=1

(µ

i,j

− (b

)/n)

= n

i=1

j=1

i,j

− 1

Поэтому значительная разница может служить основанием для отклонения

гипотезы независимости. Если гипотеза H

верна, то Z(X, Y ) ⇒ χ

(k−1)(m−1)

при n → ∞.

16.6. Контрольные вопросы

1. Что такое критерий согласия?

2. Изложите схему построения критерия согласия.

3. Можно ли проверить гипотезу о виде распределения с помощью

параметрического критерия?

4. Дайте определение критерия асимптотического уровня α.

5. Какую гипотезу проверяет критерий согласия Пирсона?

6. Какая статистика используется в критерии согласия Пирсона?

7. Какую гипотезу проверяет критерий согласия Колмогорова?

8. Какая статистика используется в критерии согласия Колмого-

рова?

9. Каковы ограничения на статистическую модель и выборку для

применения критериев согласия Пирсона и Колмогорова?

10. Сформулируйте теорему Колмогорова.

11. Сформулируйте теорему Гливенко – Кантелли.

12. Сформулируйте теорему Смирнова.

13. Какую гипотезу проверяет критерий Колмогорова – Смирнова?

153

14. Для каждого из трех текстов имеются данные о частотах, с

которыми встречаются в тексте различные служебные слова и

знаки препинания. Какой критерий можно применить для про-

верки содержательной гипотезы: «Эти три текста принадле-

жат одному автору»?

15. В условиях предыдущего вопроса какую статистику можно ис-

пользовать для проверки содержательной гипотезы: «Эти три

текста принадлежат одному автору»?

16. Датчик случайных чисел выдал N чисел 0, 1, . . . , 9. Среди них чис-

ло i встречалось n

раз (n

+. . .+n

= N). Как проверить гипотезу

о случайности чисел?

154

Лекция 17. Оценка параметров уравнения регрессии

Все модели неправильны,

но некоторые полезны.

Джордж Бокс

План лекции: метод наименьших квадратов, общая модель ли-

нейной регрессии, свойства оценок метода наименьших квадра-

тов, нормальная регрессия.

17.1. Метод наименьших квадратов

Пусть Y – случайная величина, X

, i = 1, . . . , k – контролируе-

мые (неслучайные) переменные. При этом значения величины Y зависят не

только от значений X

, но и от других факторов, в том числе таких, которые

не поддаются контролю. Поэтому для фиксированного значения X

∗

вели-

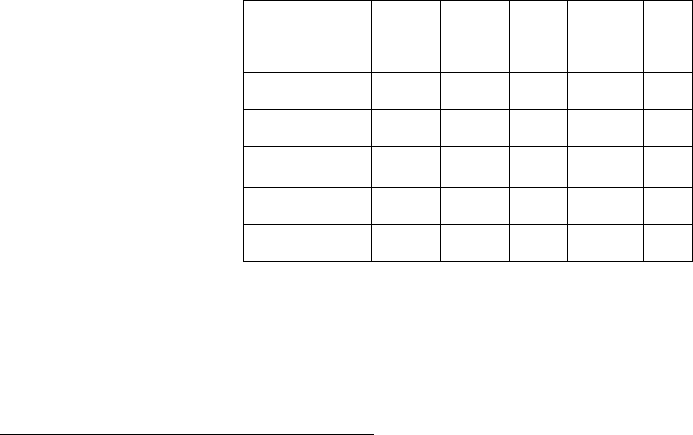
чина Y подвержена некоторому разбросу (рис. 9).

Рис. 9. Данные для отыскания регрессионной зависимости

Модель (функциональная зависимость) известна из предварительных

соображений с точностью до параметров:

Y = f(X

, . . . , X

, θ

, . . . , θ

) + ε,

где θ

, i = 1, . . . , s – параметры, ε – вектор ошибок.

Набор данных имеет вид

= f(X

, . . . , X

, θ

, . . . , θ

) + ε

. . .

= f(X

, . . . , X

, θ

, . . . , θ

) + ε

где X

– значение j-й переменной при i-м измерении. Будем считать, что

E ε = 0 и ошибки некоррелированы: K

= cov

= E(εε

) = σ

155

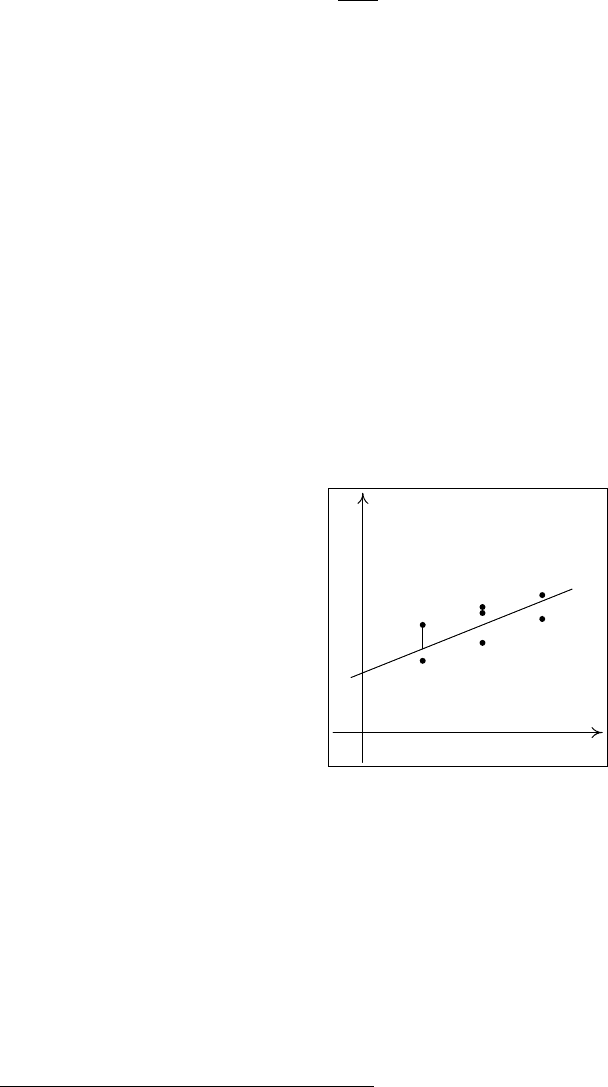
По методу наименьших квадратов (МНК) оценки параметров выби-

раются так, чтобы минимизировать сумму квадратов ошибок, то есть оце-

ниваются из условия

R =

i=1

− f(X

, . . . , X

, θ

, . . . , θ

))

→ min,

∂R

∂θ

= 0, j = 1, . . . , s.

Линия Y = f(X

, . . . , X

, θ

, . . . , θ

) называется линией регрессии Y

на X

17.2. Общая модель линейной регрессии

Наиболее часто используются линейные по параметрам модели вида

Y = θ

· a

) + θ

· a

) + . . . + θ

· a

) + ε.

(Если a

) ≡ 1, будет свободный член.)

Рассмотрим основной случай, когда a

) = X

. Одномерный случай

(k = 1) представлен на рис. 10.

Рис. 10. Иллюстрация модели линейной регрессии

В общем случае исходные данные имеют вид

= X

+ . . . + X

+ ε

. . .

= X

+ . . . + X

+ ε

или Y = X · θ + ε,

Термин «регрессия» введен Ф. Гальтоном (1886). Он установил, что особенности роста родителей про-

являются и у их детей, но в среднем в меньшей степени. У родителей низкого или высокого роста рост детей

оказывается несколько ближе к среднему, то есть (в среднем) у низких дети выше, а у высоких родителей –

ниже. Гальтон назвал это явление «возвратом» (regression).

156

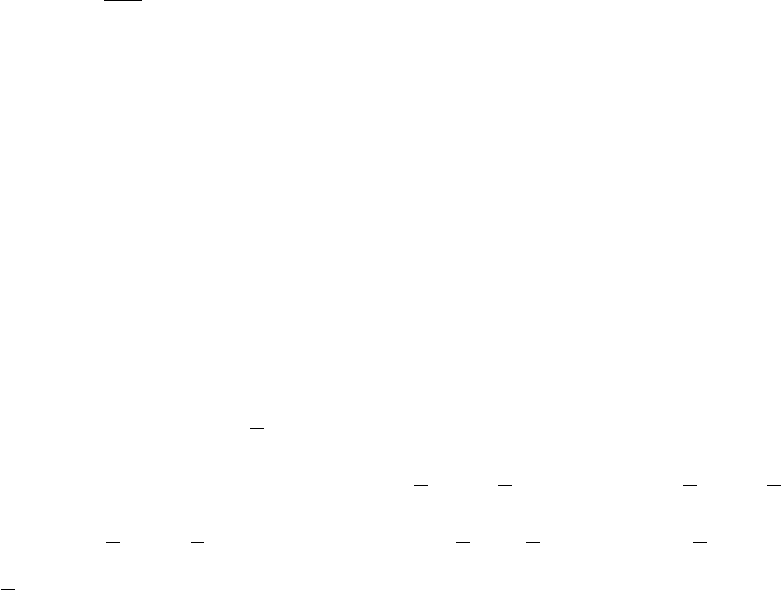
где

Y =









, X =





. . . X





, ε =









Кроме того, E ε = 0, E(εε

) = σ

Сумма квадратов ошибок или остаточная дисперсия

R = K(θ) =

−

j=1

)

→ min,

что эквивалентно

R = (Y − Xθ)

(Y − Xθ) → min .

Предположим, что матрица X

X не вырождена и найдем оценку θ из усло-

вия

∂R

∂θ

= −2

i=1

−

) = 0, l = 1, . . . , k.

Имеем

(Y − Xθ) = 0 ⇐⇒ X

Y = X

Xθ ⇐⇒

θ = (X

−1

· X

Уравнение X

Xθ = X

Y называется нормальным уравнением метода

наименьших квадратов, а

θ = (X

−1

· X

Y – оценкой параметров ли-

нейной регрессии методом наименьших квадратов (о.н.к.).

Теорема 17.1. Пусть

θ – любое решение нормального уравнения. То-

гда min R(θ) = R(

θ). Если |X

X| 6= 0, то о. н. к. единственна и равна

θ = (X

−1

· X

Y .

Доказательство. Пусть θ – произвольное фиксированное значение θ; тогда

R(θ) = (Y −Xθ)

(Y −Xθ) = [Y −Xθ + X(θ −θ)]

[Y −Xθ + X(θ −θ)] =

= R(θ) + 2(θ − θ)

Y − X

Xθ) + (θ − θ)

X(θ − θ).

При θ =

θ = (X

−1

· X

Y средний член обращается в 0 и

R(θ) = R(

θ) + (

θ − θ)

θ − θ) > R(

θ), (124)

так как матрица X

X неотрицательно определена. Равенство достигается

при θ =

θ, следовательно, это и есть точка минимума. Единственность сле-

дует из однозначной разрешимости нормального уравнения при невырож-

денной матрице X

X .

157

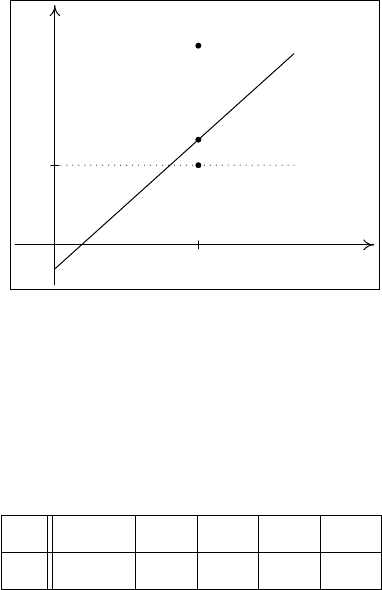
На рис. 11 изображена расчетная линия регрессии ˆy = a

+ a

x, сред-

нее значение зависимой переменной y и три точки, соответствующие задан-

ному значению переменной x

: наблюдаемое значение y

, вычисленное по

регрессии ˆy

= a

+ a

, и среднее значение ¯y.

ˆy=a

¯y

ˆy

¯y

Рис. 11. Фактическое, расчетное и среднее значения зависимой переменной y

Пример 17.1. Найдем оценку параметра линейной модели Y = X ·θ+ε

по данным:

X 0 1 2 3 4

Y −1, 2 0, 1 3, 0 4, 9 7, 3

J Напомним, что X и Y в формулах – это векторы-столбцы (как бы

ни были они заданы в условиях).

θ = (X

−1

· X

X =



0 1 2 3 4















= 30;

Y =



0 1 2 3 4









−1, 2

0, 1

3, 0

4, 9

7, 3







= 50;

θ = (X

−1

· X

Y = 5/3;

Y = 5/3X ≈ 1, 7X.

158

Пример 17.2. Найдем в условиях предыдущего примера величину

равную сумме квадратов ошибок.

R =

−

θX

)

−

)

где

– значения, вычисленные по уравнению регрессии

Y = 1, 7X.

X 0 1 2 3 4

Y −1, 2 0, 1 3, 0 4, 9 7, 3

Y 0 1, 7 3, 4 5, 1 6, 8

|Y −

Y | 1, 2 1, 6 0, 4 0, 2 0, 5

R =

−

)

= 4, 45.

Пример 17.3. Найдем по данным примера 17.1 оценки параметров ли-

нейной модели

Y = X ·θ + θ

+ ε.

J Будем считать, что переменная X двумерна, и рассматривать модель Y =

· θ + X

+ ε, где X

≡ 1.

0 1 2 3 4

1 1 1 1 1

Y −1, 2 0, 1 3, 0 4, 9 7, 3

θ = (X

−1

· X

X =



30 10

10 5



; (X

−1

= 1/50 ·



5 −10

−10 30





0, 1 −0, 2

−0, 2 0, 6



Y =



0 1 2 3 4

1 1 1 1 1









−1, 2

0, 1

3, 0

4, 9

7, 3









14, 1



θ = (X

−1

· X

Y =



0, 1 −0, 2

−0, 2 0, 6





14, 1





2, 18

−1, 54



;

159

Y = 2, 18X − 1, 54.

Рис. 12. Графическое изображение данных (примеры 17.1–17.3)

Найдем для этой модели величину

R, равную сумме квадратов оши-

бок:

R =

−

j=1

)

−

)

где

– значения, вычисленные по уравнению регрессии

Y = 2, 18X −1, 54

(рис. 12).

X 0 1 2 3 4

Y −1, 2 0, 1 3, 0 4, 9 7, 3

Y −1, 54 0, 64 2, 82 5 7, 18

|Y −

Y | 0, 34 0, 54 0, 18 0, 1 0, 12

R =

−

)

= 0, 4640.

Как видим, ошибка при использовании модели со свободным членом

примерно в 10 раз меньше. Причина этого понятна из рис. 12. Очевидно,

модель без свободного члена (Y = X ·θ + ε) не является адекватной. I

В одномерном случае для нахождения параметров линейной модели

Y = X ·θ +θ

+ε удобно использовать следующие формулы, получаемые из

160