Крупкина Т.В. Математическая статистика
Подождите немного. Документ загружается.


Теорема 1.2. В модели hF
ξ
i
F
X
∗
k
(x) =
n
X
i=k
C
i
n
F
i
ξ
(x)(1 − F
ξ
(x))
n−i
.
Доказательство.
F
X
∗
k
(x) = P(X
∗
k
< x) = P(ν
n
(x) > k) =
=
n
X
i=k
P(ν
n
(x) = i) =
n
X
i=k
C
i
n
F
i
ξ
(x)(1 − F
ξ
(x))
n−i
.
Эмпирическая частота равна абсолютному числу элементов выбор-
ки, меньших x. В качестве приближения функции распределения F
ξ
(x) це-
лесообразно взять относительную частоту попадания случайных величин
(X
1
, . . . , X
n
) в интервал (−∞, x).
Определение 1.4. Эмпирической функцией распределения F
n
(x),
соответствующей выборке X, называется случайная функция от x,
вычисляемая по формуле
F
n
(x) =
ν
n
n
, (3)
где ν
n
– число элементов выборки X = (X
1
, . . . , X
n
), значения кото-
рых меньше x.
Следовательно, эмпирическая функция распределения – сжатая характе-
ристика выборки. Для каждой реализации x = (x
1
, . . . , x
n
) функция F
n
(x)
однозначно определена и обладает всеми свойствами функции распределе-
ния: изменяется от 0 до 1; не убывает; непрерывна слева; F
n
(x) = 0 при
x 6 x
∗
1
и F
∗
n
(x) = 1 при x > x
∗
n
. При этом она кусочно-постоянна и воз-
растает только в точках последовательности (2). Если все составляющие
вектора x различны, то
F
n
(x) =
0 при x 6 x
∗
1
,
k
n
при x
∗
k
< x 6 x
∗
k+1
, k = 1, . . . , n − 1,
1 при x > x
∗
n
.
(4)
Заметим, что эмпирическая функция распределения имеет скачки в
точках выборки, величина скачка в точке x
∗
i
равна 1/n. Если же элемент
x
∗
i
встречается m раз, то величина скачка равна m/n.
График функции F
n
(x) имеет вид, изображенный на рис. 1.
11
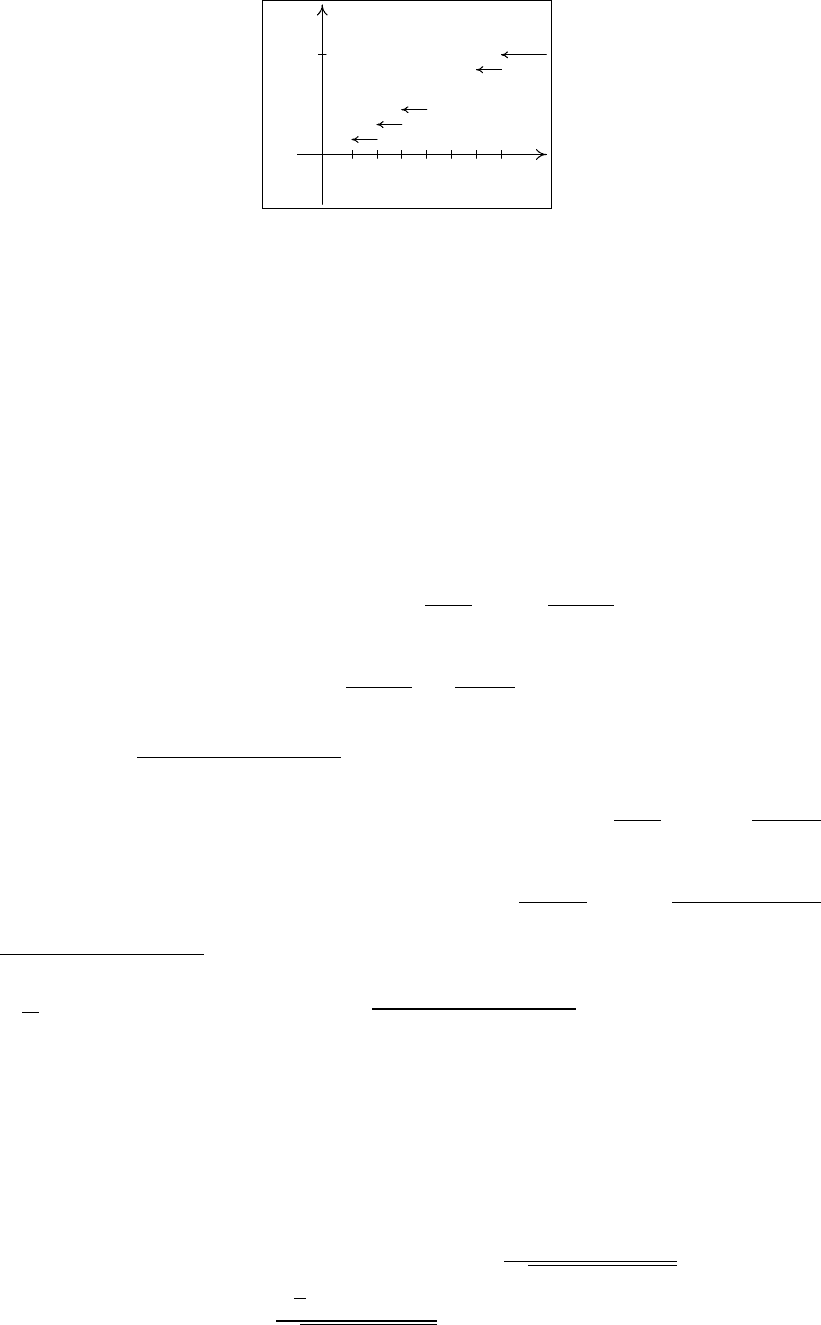
F
n
(x)
XO
x
∗
1
x
∗
2
x
∗
3
x
∗
n
. . .
. . .
Рис. 1. Эмпирическая функция распределения
Эмпирическая функция распределения обладает важным свойством:
при увеличении числа испытаний над случайной величиной ξ (увеличении
объема выборки X ) она сближается с теоретической функцией F (x), то
есть ее можно считать статистическим аналогом для F (x). Это показывают
следующие свойства.
1. E F
n
(x) = F
ξ
(x).
Доказательство. E F
n
(x) = E
ν
n
(x)
n
=
E ν
n
(x)
n
, но ν
n
(x) имеет би-
номиальное распределение B(n; F
ξ
(x)) с математическим ожиданием
nF
ξ
(x). Поэтому E F
n
(x) =
E ν
n
(x)
n
=
nF
ξ
(x)
n
= F
ξ
(x).
2. D F
n
(x) =
F
ξ
(x)(1 − F
ξ
(x))
n
.
Доказательство. Аналогично D F
n
(x) = D
ν
n
(x)
n
=
D ν
n
(x)
n
2
, но
ν
n
(x) имеет биномиальное распределение B(n; F
ξ
(x)) с дисперси-
ей nF
ξ
(x)(1 − F
ξ
(x)), и D F
n
(x) =
D ν
n
(x)
n
2
=
nF
ξ
(x)(1−F
ξ
(x))
n
2
=
F
ξ
(x)(1 − F
ξ
(x))
n
.
3.
√
n(F
n
(x) − F
ξ
(x)) ∼ N
0;
p
F
ξ
(x)(1 − F
ξ
(x))
.
Доказательство. Асимптотическая нормальность следует из ЦПТ,
так как величину nF
n
(x) = ν
n
(x) можно представить в виде суммы
независимых случайных величин, имеющих распределение Бернулли
B(1, F
ξ
(x)) (каждое слагаемое при этом является индикатором I собы-
тия {X
i
< x}). По ЦПТ для суммы одинаково распределенных незави-
симых случайных величин справедливо:
n(F
n
(x)−F
ξ
(x))
√
nF
ξ
(x)(1−F
ξ
(x))
d
−→ u ∈ N(0, 1).
Отсюда следует, что
√
n(F
n
(x)−F
ξ
(x))
√
F
ξ
(x)(1−F
ξ
(x))
d
−→ u ∈ N(0, 1), что и означает
асимптотическую нормальность.
12

4. F
n
(x)
p
−→ F
ξ
(x).
Доказательство. Это следует, например, из ЗБЧ в форме Бернулли,
так как эмпирическая функция распределения F
n
(x) – это частота со-
бытия {X < x}, а F
ξ
(x) – вероятность этого события. Можно также
сослаться на свойство среднего арифметического n независимых сла-
гаемых, имеющих распределение Бернулли (ЗБЧ в форме Хинчина).
5. F
n
(x)
п.н.
−−→ F
ξ
(x).
Доказательство. Следует из выполнимости УЗБЧ в форме Бореля.
Рассмотрим еще несколько важных свойств эмпирической функции
распределения. Справедливы следующие теоремы [1, 2, 24].
Теорема 1.3 (теорема Гливенко). Пусть F
n
(x) – эмпирическая функ-
ция распределения, построенная по выборке X = (X
1
, . . . , X
n
) из рас-
пределения F
ξ
, и F (x) – соответствующая теоретическая функция
распределения. Тогда для любого −∞ < x < ∞
P( lim
n→∞
D
n
= 0) = 1, (5)
где
D
n
= D
n
(x) = sup
−∞<x<∞
|F
n
(x) − F (x)|. (6)
Приведем еще две предельные теоремы для эмпирической функции
распределения, имеющие важное значение для проверки различных пред-
положений (гипотез) о выборках.
Теорема 1.4 (теорема Колмогорова). Если функция F (x) непрерывна,
то при любом фиксированном t > 0
lim
n→∞
P(|
√
nD
n
< t|) = K(t) =
∞
X
j=−∞
(−1)
j
e
−2j
2
t
2
, (7)
Функция K(t) называется функцией Колмогорова, и ее можно с хоро-
шим приближением использовать для практических расчетов уже при объ-
еме выборки, равном или большим 20. Заметим, что теорема справедлива
для любой непрерывной функции распределения и позволяет найти грани-
цы, в которых с заданной вероятностью 0 < α < 1 находится теоретическая
функция F (x) (она в нашей статистической модели неизвестна). Если зада-
на вероятность α, то при больших n с вероятностью, близкой к α, функция
F (x) удовлетворяет неравенству
|F
n
(x) − F (x)| 6
t
α
√
n
, (8)
13

где величина t
α
вычисляется как корень уравнения K(t) = α с помощью
таблиц для функции K(t). Обоснование данного неравенства можно найти
в [24].
Теорема 1.5 (теорема Смирнова). Пусть F
n
(x) и F
m
(x) – две эмпири-
ческие функции распределения, построенные на основе двух незави-
симых выборок объемов n и m из одного и того же распределения F
ξ
,
и
D
n,m
= sup
−∞<x<∞
|F
n
(x) − F
m
(x)|. (9)
Тогда если теоретическая функция F (x) непрерывна, то для любого
фиксированного t > 0
lim
n,m→∞
P(
p
nm/(n + m) D
n,m
6 t) = K(t), (10)
где функция K(t) определена равенством (7).
Эта теорема позволяет ответить на важный практический вопрос,
можно ли считать, что две выборки получены из одного и того же распреде-
ления.
Замечание 1.2. Поскольку эмпирическая функция распределения
близка к теоретической, выборочные характеристики (выборочное
среднее, выборочная дисперсия и другие) можно рассматривать как
обычные характеристики (математическое ожидание, дисперсия
и другие) случайной величины, принимающей значения X
1
, . . . , X
n
с равными вероятностями
1
n
. Таким образом, простую выборку
можно рассматривать не только как n-мерную случайную величину
(X
1
, . . . , X
n
), но и как одномерную дискретную величину:
X X
1
X
2
. . . X
n
P 1/n 1/n . . . 1/n
.
1.5. Контрольные вопросы
1. Какая статистическая модель применима для выборки, получен-
ной следующим образом: 10 раз подсчитывалось число гербов при
бросании трех монет?
2. Какая статистическая модель применима для выборки действу-
ющих цен на литр молока в 50 различных магазинах г. Краснояр-
ска?
14
3. Дайте определение параметрической модели.
4. Является ли модель N(a, θ) параметрической?
5. Дайте определение регулярной модели.
6. Является ли модель R[θ, b] регулярной?
7. Дайте определение вариационного ряда реализации.
8. Дайте определение вариационного ряда выборки.
9. Можно ли восстановить по вариационному ряду выборку?
10. Дайте определение эмпирической функции распределения.
11. Какими свойствами обладает эмпирическая функция распреде-
ления?
12. Можно ли восстановить по эмпирической функции распределе-
ния вариационный ряд?
13. Верно ли, что все элементы простой выборки одинаково распре-
делены?
14. Верно ли, что все элементы вариационного ряда одинаково рас-
пределены?
15

Лекция 2. Основные выборочные характеристики
Дело не в числах, а в том, что вы с ними делаете.
К. Мэндервилл
План лекции: выборочные моменты, соответствие выборочных
и теоретических характеристик, свойства X и S
2
, другие харак-
теристики выборки, сходимость выборочных моментов.
2.1. Выборочные моменты и функции от выборочных моментов
Пусть X = (X
1
, . . . , X
n
) – выборка объема n из распределения F и
x = (x
1
, . . . , x
n
) – наблюдавшееся значение X. Любая функция от X пред-
ставляет собой также случайную величину с распределением, однозначно
определяемым распределением вектора X. В теории вероятностей введены
определения различных моментов случайной величины. Так, начальным мо-
ментом порядка k случайной величины ξ называется число
α
k
= E(ξ)
k
, (11)
а центральным моментом порядка k случайной величины ξ называется чис-
ло
µ
k
= E(ξ − E ξ)
k
. (12)
Введем общее обозначение для моментов: E g(ξ) (g(ξ) = (ξ)
k
для началь-
ных моментов и (ξ − E ξ)
k
для центральных моментов k-го порядка). Каж-
дому теоретическому моменту g(ξ) можно поставить в соответствие его ста-
тистический аналог G = G(X), вычисляемый по формуле
G(X) =
1
n
n
X
i=1
g(X
i
).
Случайную величину G называют эмпирической или выборочной
характеристикой, соответствующей теоретической характеристике g.
Если g(ξ) = ξ
k
, то G – выборочный начальный момент k-го поряд-
ка, который будем обозначать a
k
.
Определение 2.1. Выборочным начальным моментом k-го поряд-
ка называют случайную величину
a
k
=
1
n
n
X
i=1
X
k
i
. (13)
16
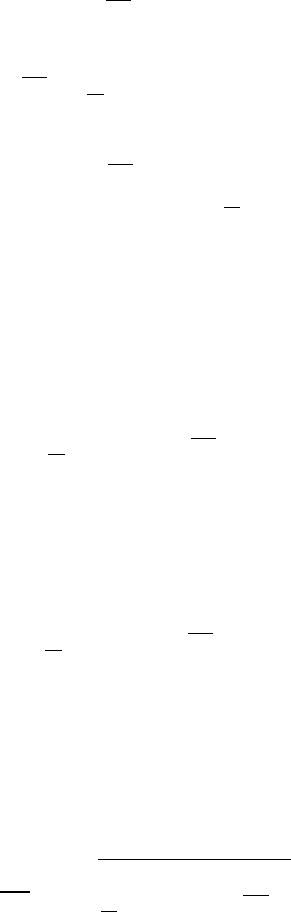
Определение 2.2. Если k = 1, то величину a
1
называют выборочным
средним и обозначают символом X,
X =
1
n
n
X
i=1
X
i
.
Значения случайной величины X при конкретной реализации x вы-
борки X будем обозначать строчной буквой (x). Напомним, что теорети-
ческие моменты случайной величины ξ обозначают греческими буквами, а
соответствующие им выборочные – латинскими.
Определение 2.3. Выборочным центральным моментом k-го по-
рядка называют случайную величину
m
k
=
1
n
n
X
i=1
(X
i
− X)
k
. (14)
Определение 2.4. При k = 2 величину m
2
называют выборочной дис-
персией и обозначают S
2
:
S
2
=
1
n
n
X
i=1
(X
i
− X)
2
.
Выборочная дисперсия характеризует разброс значений.
Определение 2.5. Выборочным среднеквадратическим отклоне-
нием называют случайную величину
S =
√
S
2
=
v
u
u
t
1
n
n
X
i=1
(X
i
− X)
2
.
Среднеквадратическое отклонение – линейная мера разброса вы-
борочных значений. При рассмотрении свойств плотности распределения
непрерывных величин вводили такие характеристики, как коэффициенты
асимметрии A и эксцесса E. Если график плотности распределения сим-
метричен, то A = 0. По значению A судят о степени отклонения от симмет-
рии, по знаку A – о правосторонней (A > 0) или левосторонней (A < 0)
асимметрии.
Для нормального распределения E = 0, и поэтому о кривых плотности
с E = 0 говорят, что у них нормальный эксцесс. Если E > 0 (E < 0), то
эксцесс кривой положительный, то есть кривая плотности островершинна
(отрицательный, то есть кривая плотности плосковершинна).
17

Пусть задана выборка X из распределения непрерывной случайной
величины ξ. Тогда для нее можно определить выборочные коэффициенты
асимметрии
b
A и эксцесса
b
E по следующим формулам.
Определение 2.6. Выборочным коэффициентом асимметрии назы-
вается величина
b
A =
m
3
S
3
. (15)
Определение 2.7. Выборочным коэффициентом эксцесса называется
величина
b
E =
m
4
S
4
− 3. (16)
Аналогично можно ввести и другие характеристики, например, абсо-
лютные моменты. Необходимо помнить, что выборочные характеристики
вводятся соответственно теоретическим характеристикам случайной вели-
чины (табл. 2).
Таблица 2
Соответствие выборочных и теоретических характеристик
Теоретические характеристики Выборочные характеристики
a = E ξ X =
1
n
P
n
i=1
X
i
математическое ожидание выборочное среднее
σ
2
= D ξ S
2
=
1
n
P
n
i=1
(X
i
− X)
2
дисперсия выборочная дисперсия
α
k
= E ξ
k
a
k
=
1
n
P
n
i=1
X
k
i
начальный k-й момент начальный выборочный k-й момент
µ
k
= E(ξ − E ξ)
k
m
k
=
1
n
P
n
i=1
(X
i
− X)
k
центральный k-й момент центральный выборочный k-й момент
A =
µ
3
σ
3
b
A =
m
3
S
3
коэффициент асимметрии выборочный коэффициент асимметрии
E =
µ
4
σ
4
− 3
b
E =
m
4
S
4
− 3
коэффициент эксцесса выборочный коэффициент эксцесса
2.2. Свойства выборочного среднего X и S
2
Выборочные характеристики являются случайными величинами, и
поэтому можно говорить о их распределениях (выборочных распределени-
ях) и изучать различные характеристики этих распределений.
18
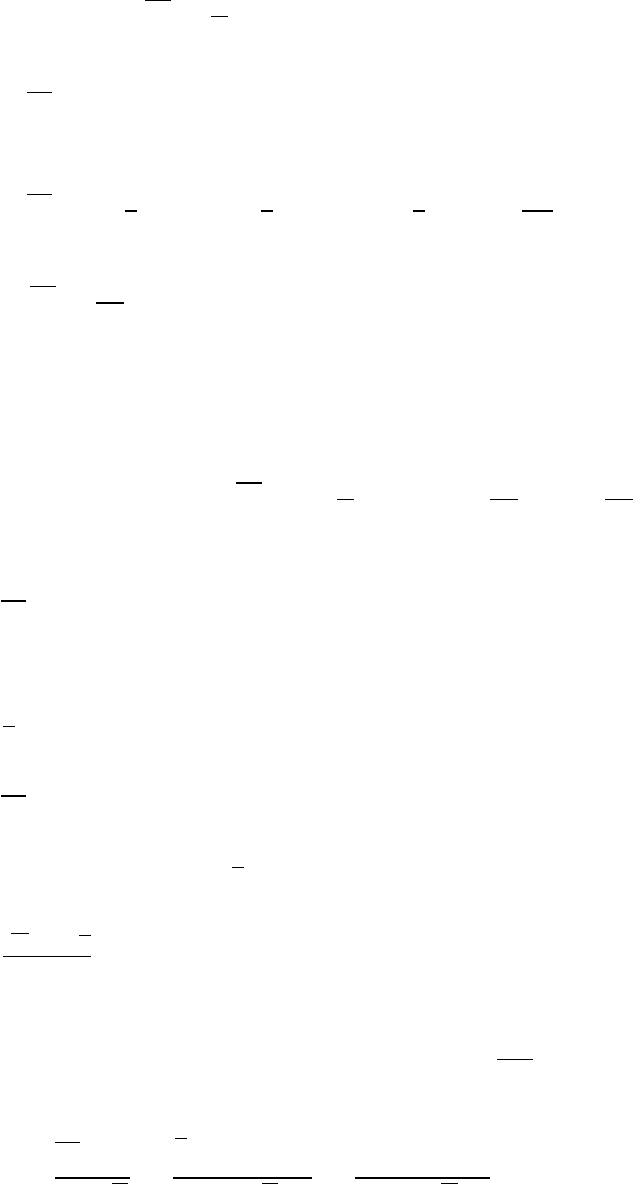
Будем считать, что выборка взята из совокупности с математическим
ожиданием E ξ = a и дисперсией D ξ = σ
2
; тогда E X
i
= a, D X
i
= σ
2
для
любого элемента выборки X
i
, при этом случайные величины X
i
независимы.
Свойства X =
1
n
n
P
i=1
X
i
.
1. E X = a.
Доказательство.
E X = E(
1
n
P
X
i
) =
1
n
P
E X
i
=
1
n
P
a =
na
n
= a.
2. D X =
σ
2
n
.
Доказательство.
Поскольку X
i
независимы и распределены так же, как случайная ве-
личина ξ, то
D X = D(
1
n
X
X
i
) =
1
n
2
nσ
2
=
σ
2
n
.
3. X
p
−→ a.
Доказательство.
1
n
n
P
i=1
X
i
p
−→ a, по ЗБЧ в форме Хинчина.
4. X
п.н.
−−→ a.
Доказательство.
1
n
n
P
i=1
X
i
p
−→ a, по критерию УЗБЧ Колмогорова.
5.
(X−a)
√
n
σ
∼ N(0, 1).
Доказательство.
Согласно обозначениям ξ ∼ N(a, σ)
ξ−a
σ
d
−→ u ∈ N(0, 1),
X − a
σ/
√
n
=
1
n
n
P
i=1
X
i
− a
σ/
√
n
=
n
P
i=1
X
i
− na
σ/
√
n
d
−→ u ∈ N(0, 1), по ЦПТ.
Рассмотрим свойства выборочной дисперсии S
2
.
19
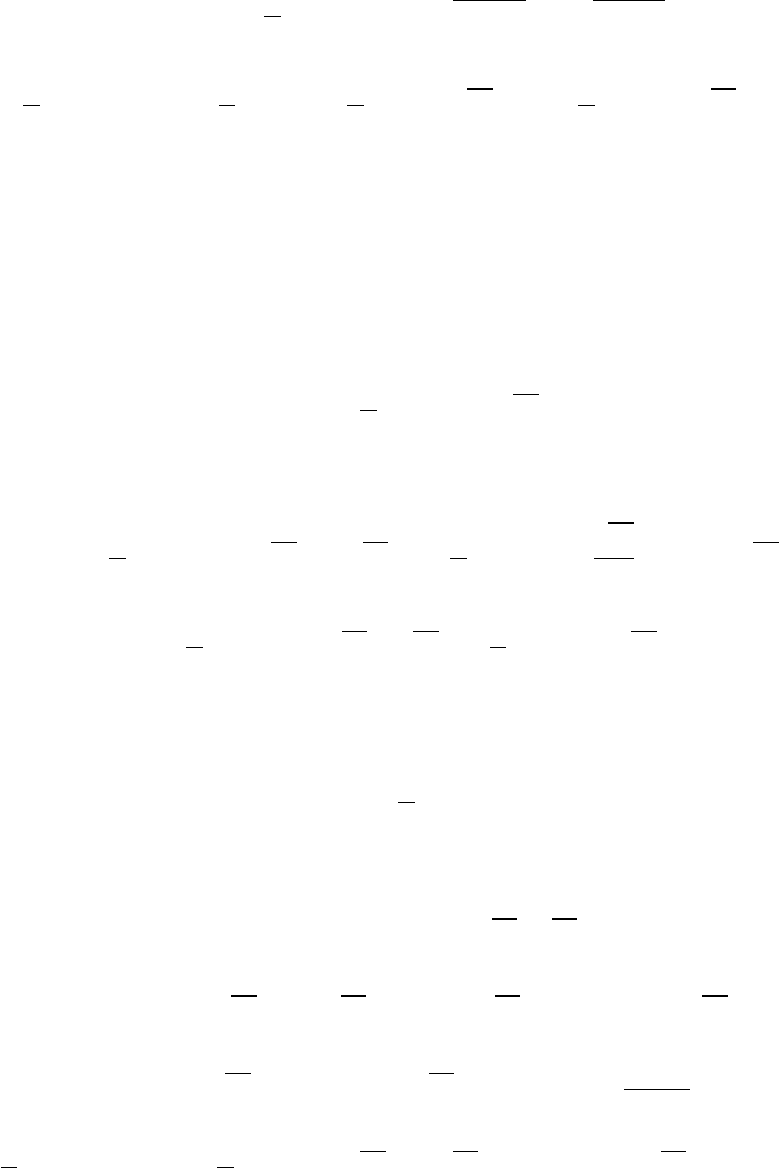
1.
S
2
X+c
= S
2
X
.
Доказательство.
S
2
X+c
=
1
n
X
(X
i
+ c − X + c)
2
= [X + c =
=
1
n
X
(X
i
+c) =
1
n
X
X
i
+
1
n
X
c = X +c] =
1
n
X
(X
i
−X)
2
= S
2
X
.
2.
S
2
kX
= k
2
S
2
X
.
Доказывается аналогично.
3.
S
2
=
1
n
X
X
2
i
− (X)
2
.
Доказательство.
S
2
=
1
n
X
(X
2
i
− 2XX
i
+ X
2
) =
1
n
X
X
2
i
−
2X
n
X
X
i
+ X
2
=
=
1
n
X
X
2
i
− 2X
2
+ X
2
=
1
n
X
X
2
i
− X
2
.
4.
S
2
= min
c
1
n
X
(X
i
− c)
2
.
Доказательство.
X
(X
i
− c)
2
=
X
(X
i
− X + X − c)
2
=
X
(X
i
− X)
2
+ n(X − c)
2
+ 2(X − c)
X
(X
i
− X),
X
(X
i
− X) =
X
X
i
− nX =
X
X
i
− n
P
X
i
n
= 0,
1
n
X
(X
i
− c)
2
=
1
n
X
(X
i
− X)
2
+ (X − c)
2
= S
2
+ (X − c)
2
> S
2
.
20
