Крупкина Т.В. Математическая статистика

Подождите немного. Документ загружается.

СПРАВКА. Квантили N(0, 1) : u

0,.95

= 1, 64, u

0,975

= 1, 96, u

0,995

= 2, 58.

Пример 11.2. В условиях предыдущего примера как изменился бы до-

верительный интервал, если бы те же данные были получены по 25

группам численностью 100 человек каждая?



X −

√

· u

1−

; X +

√

· u

1−





60 −

√

· u

0,975

; 60 −

√

· u

0,975





60 −

· 1, 96; 60 −

· 1, 96



= [60 − 3, 92; 60 + 3, 92] = [56, 08; 63, 92].

Длина интервала равна 3, 92 · 2 = 7, 84, а в предыдущем примере длина до-

верительного интервала равнялась 9, 8 · 2 = 19, 6, то есть новый интервал в

2,5 раза короче.I

11.5. Асимптотические доверительные интервалы

Надпись «Нет в жизни счастья» он смыл бесповоротно.

Счастье было! Вот оно было! Прямо перед нами!

Ю. Коваль, «Суер-Выер»

Параметр произвольного распределения можно оценить так же, как

параметр нормального распределения, если известно распределение неко-

торой статистики, зависящей от параметра и его оценки (эту информацию

можно найти в справочниках, а можно вывести самим). Другой способ свя-

зан с использованием асимптотического метода (это и есть заявленное

счастье. Почти всегда можно обойтись нормальным распределением). Если

θ асимптотически нормальна и несмещена (например, является о.м.п.), то

θ − θ

→ u ∈ N(0, 1).

1 − α = p

θ − θ

6 u

1−

. (101)

101

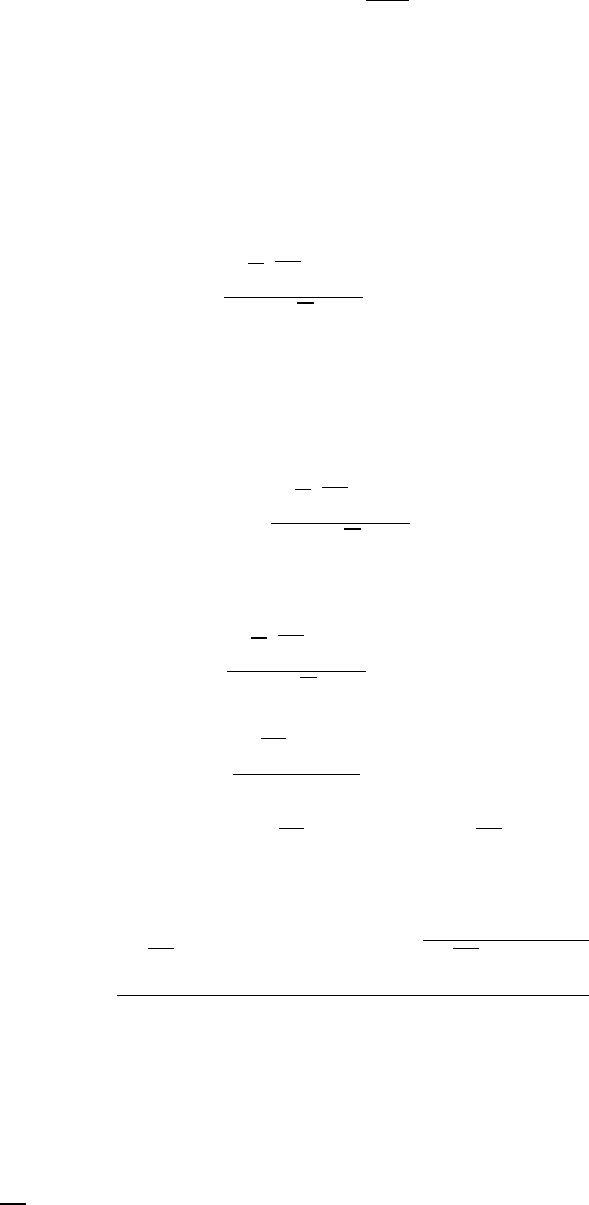
Разрешим относительно θ, получим доверительный интервал значимости α.

Кстати, длина его пропорциональна

θ и минимальна, когда минимальна

θ, то есть при эффективной

θ.

Пример 11.3. Построим асимптотический доверительный интервал

для параметра распределения Пуассона λ уровня значимости α.

J Для этого рассмотрим статистику

S =

√

n(X − λ)

√

→ u ∈ N(0, 1)

и найдем из уравнения P (I

6 λ 6 I

) = 1 − α доверительный интервал

, I

P (u

α/2

6 S 6 u

1−α/2

) = 1 − α;

α/2

√

n(X − λ)

√

6 u

1−α/2

Так как −u

α/2

= u

1−α/2

, то



√

n(X − λ)

√



6 u

1−α/2

n(X − λ)

6 u

1−α/2

nλ

− λ(2nX + u

1−α/2

) + nX

6 0.

Решая относительно λ последнее неравенство, получаем интервал



2nX + u

1−α/2

± u

1−α/2

4nX + u

1−α/2



Замечание 11.2. Точный доверительный интервал для параметра

распределения Пуассона λ можно найти, используя точное распре-

деление X.

Пример 11.4. Найдем асимптотический доверительный интервал

для параметра λ показательного распределения E

уровня значимо-

сти α.

102

J Вспомним, что о.м.п. λ равна

λ =

. Чтобы не искать дисперсию

изменим параметризацию, возьмем за параметр

. В силу инвариантности

о.м.п., оценка

равна X. Тогда

√

X −

√

n(λX − 1)

−→ u ∈ N(0, 1),

и дальше, как в предыдущих примерах (только вычисления проще).I

11.6. Контрольные вопросы

1. Чем отличается интервальная оценка от точечной?

2. Дайте определение доверительного интервала.

3. Что выражает уровень значимости?

4. Что выражает доверительная вероятность?

5. Как связана доверительная вероятность с длиной доверитель-

ного интервала?

6. Дайте определение центральной статистики.

7. В чем состоят преимущества использования центральной ста-

тистики для построения доверительного интервала?

8. В чем отличия доверительных интервалов математического

ожидания нормального распределения при известной и неиз-

вестной дисперсии?

9. Какой информацией надо располагать, чтобы построить дове-

рительный интервал для математического ожидания нормаль-

ного распределения?

103

Лекция 12. Основные понятия теории проверки гипотез

Чтобы правильно задать вопрос,

надо знать большую часть ответа.

Роберт Шекли

План лекции: основные понятия, примеры математических фор-

мулировок гипотез, общая схема проверки параметрических ги-

потез, ошибки первого и второго рода, мощность критерия.

12.1. Основные понятия

Определение 12.1. Статистической гипотезой (в дальнейшем

просто гипотезой) называется любое утверждение о виде или свой-

ствах распределения наблюдаемых в эксперименте случайных вели-

чин.

Задача разработки рациональных методов проверки статистических

гипотез – одна из основных в математической статистике.

Если для исследуемого явления (процесса, стратегии) сформулиро-

вана та или иная гипотеза H

(основная, нулевая), то задача состоит в том,

чтобы сформулировать такое правило, которое позволяло бы по имеющим-

ся результатам наблюдений отклонить или принять (точнее, не отклонить)

эту гипотезу.

Нулевая гипотеза H

обычно соответствует естественному, наиболее

ожидаемому состоянию (норме).

Определение 12.2. Правило, согласно которому проверяют гипоте-

зу H

(отвергают или не отвергают), называется статистиче-

ским критерием проверки гипотезы H

Таким образом, разработка правил и их обоснование с точки зрения опти-

мальности и составляюет предмет теории проверки статистических гипотез.

Определение 12.3. Любая гипотеза о распределении наблюдаемой

случайной величины, которая может оказаться истинной, но отли-

чается от основной гипотезы, называется альтернативной гипо-

тезой.

Определение 12.4. Статистическая гипотеза называется про-

стой, если однозначно фиксирует распределение наблюдений. Иначе

это сложная гипотеза.

104

Основная идея проверки статистической гипотезы: чтобы постро-

ить критерий, возьмем статистику T = T (X) (функцию от результатов на-

блюдений), такую, что известно ее распределение при условии, что прове-

ряемая гипотеза H

верна. Если же гипотеза H

не верна, распределение T

должно отличаться от распределения T/H

(распределения T при условии,

что верна H

). Эта функция T , являющаяся случайной величиной, называ-

ется статистикой критерия. Дальше мы вычислим значение статистики T по

выборке. Поскольку известно распределение T/H

, можно оценить вероят-

ность наблюдаемого значения. И если эта вероятность слишком мала, мы

делаем вывод, что столь маловероятное значение не должно было наблю-

даться. Но оно наблюдается, это факт. Следовательно, распределение, из

которого мы исходили, T/H

– неверно. Значит, неверна гипотеза H

и она

отвергается.

Разумеется, принятое решение может быть ошибочным (например,

случайно произошло маловероятное событие). Ошибки, которые могут воз-

никать при проверке гипотез, будут подробно рассмотрены позднее.

12.2. Примеры математических формулировок гипотез

Количество разумных гипотез, способных

объяснить любой феномен, бесконечно.

Постулат гипотез

1. Гипотеза о виде распределения. Пусть проводят n независимых на-

блюдений над некоторой случайной величиной ξ с неизвестной функ-

цией распределения F (x). Нулевая гипотеза может иметь вид

: F (x) = F

(x),

где F

(x) полностью задана, или

: F (x) ∈ {F},

где {F} – заданное семейство функций распределения. При этом

обычно семейство {F} задают в параметрическом виде: {F

}. Здесь

= F (x, θ).

2. Гипотеза однородности. Произведено k серий независимых наблю-

дений. Если можно считать, что закон распределения наблюдений от

серии к серии не меняется, то говорят, что статистические данные од-

нородны. Пусть F

(x) – функция распределения

наблюдений l-й се-

Функции распределения наблюдений, как правило, неизвестны, а то мы бы просто их сравнили. Задача

как раз в том, чтобы сравнить их не зная.

105

рии, l = 1, . . . , k. Гипотеза однородности имеет вид

: F

(x) ≡ ··· ≡ F

(x).

3. Гипотеза независимости. Наблюдается двумерная случайная величи-

на (ξ, η) с неизвестной функцией распределения F

ξ,η

(x, y), проверяется

предположение о независимости компонент (ξ, η):

: F

ξ,η

(x, y) = F

(x)F

(y).

4. Гипотеза случайности. Результат эксперимента описывают случай-

ной n-мерной величиной X = (X

, . . . , X

) с неизвестной функцией

распределения F (x). Для выяснения, можно ли рассматривать X как

случайную выборку из распределения некоторой случайной величины

ξ (то есть являются ли компоненты X

независимыми и одинаково рас-

пределенными), проверяют гипотезу случайности:

: F = F

= ··· = F

= F

5. Параметрические гипотезы. Это один из наиболее важных классов

гипотез

Определение 12.5. Статистическая гипотеза называется па-

раметрической, если она представляет собой предположение о

том, что неизвестный параметр распределения имеет наперед

заданное значение или множество значений.

Под параметром θ, как обычно, понимается вектор θ = (θ

, . . . , θ

). В этом

случае класс допустимых распределений наблюдаемой случайной величи-

ны ξ имеет вид {F (x, θ

), . . . , F (x, θ

)} и гипотезы относятся к неизвестным

скалярным параметрам θ

, i = 1, . . . , r – ко всем или к части их.

Рассмотрим несколько вариантов параметрических гипотез.

Пример 12.1.

1. H

: θ

= ··· = θ

2. H

: θ = θ

, где θ

– фиксированное известное значение.

3. H

: g(θ) = g(θ

), где g(t) – функция.

Надо иметь в виду, что рассмотренные примеры не представляют из себя исчерпывающего перечня воз-

можных гипотез.

106

Пример 12.2.

J H

: θ

∈ Θ

(сложная гипотеза).

Альтернативная гипотеза : H

: θ = θ

, где θ

6= θ

– простая гипотеза,

а варианты θ > θ

или θ < θ

или θ ∈ Θ

задают сложные альтернативные

гипотезы.I

Пример 12.3. Для нормального распределения N(θ

, θ

J H

: θ

= θ

, θ

= θ

– простая гипотеза, а

: θ

= θ

– сложная гипотеза, так как θ

– свободный параметр.I

12.3. Общая схема проверки параметрических гипотез

Природа в ответ на наши вопросы

отвечает «нет» громко, а «да» тихо.

Фольклор

Рассмотрим процесс проверки гипотезы на примере параметрической

гипотезы.

Пусть (X

, . . . , X

) – выборка объема n из распределения F (x, θ),

θ ∈ Θ, а (x

, . . . , x

) – реализация. Сформулированы гипотезы (сложные

в общем виде):

: θ ∈ Θ

– нулевая, H

: θ ∈ Θ

– альтернативная.

Пока будем для ясности рассматривать простые гипотезы, когда каж-

дое из множеств Θ

, Θ

содержит только одну точку:

: θ = θ

– нулевая, H

: θ = θ

– альтернативная.

Необходимо построить критерий, то есть правило, по которому для

каждой реализации x можно было бы принять H

или отвергнуть H

(при-

нять H

). Тем самым выборочная область X = {(x

, . . . , x

)} разбивается

на две части V и V :

V ∩ V = ∅, V ∪ V = X,

где V состоит из тех (x

, . . . , x

), для которых H

принимают, а множество

V состоит из тех (x

, . . . , x

), для которых принимают H

. Множество V на-

зывают областью принятия гипотезы H

, а V – областью ее отклонения или

критической областью.

Тогда критерий формулируется следующим образом: пусть x – на-

блюдаемая реализация выборки, тогда при x ∈ V гипотезу H

отвергают

(в пользу альтернативной гипотезы H

); если же x ∈ V , то H

не отвергают.

107

Обратите внимание: если x ∈ V , то гипотезу H

отвергают (громкое

«нет»). В противном случае (x /∈ V ) мы не можем утверждать, что гипотеза

подтвердилась, тем более – что она доказана, можно сказать только, что

гипотеза H

не отвергается (тихое «да»). С практической точки зрения это

означает, что гипотезу H

можно использовать дальше и опираться на нее

при получении различных выводов.

Для простоты мы будем иногда говорить о принятии гипотезы, вкла-

дывая в это смысл «гипотеза не отвергается».

Критерий, определяемый критической областью V , называют крите-

рием K

Обозначим через H

статистическое решение, тогда определение кри-

терия 12.2 может быть конкретизировано следующим образом:

(x) = H

(x) =



, x ∈ V,

, x ∈ V .

Обычно критическую область V задают с помощью статистики T (x),

для которой распределение известно точно или приближенно. Однако нет

необходимости непременно связывать понятие критерия со статистикой,

поскольку в конечном счете нас интересует соответствие между x и прини-

маемым статистическим решением. Это соответствие можно задать функ-

цией ϕ(x), которая принимает значение 1, когда следует отвергнуть H

, и

значение 0, когда H

не отвергается:

(x) = H

(x) =



, ϕ(x) = 1,

, ϕ(x) = 0.

(102)

В процессе проверки гипотезы можно принять правильное решение

или совершить ошибку.

12.4. Ошибки первого и второго рода

Авторизованный пользователь классифицируется как нарушитель

– ошибка первого рода,

нарушитель классифицируется как авторизованный пользователь

– ошибка второго рода.

Рольф Т. Моултон

Определение 12.6. Вероятностью ошибки первого рода называет-

ся вероятность отклонить H

, когда H

верна.

108

Эта вероятность обозначается α и называется еще уровнем значи-

мости

критерия или размером критерия. Очевидно,

α = P (H

= H

) = P (X ∈ V/H

(α равняется вероятности того, что X принадлежит критической области V

при условии, что верна H

Определение 12.7. Вероятностью ошибки второго рода называ-

ется вероятность принять H

, когда H

не верна.

Вероятность ошибки второго рода обозначается β. Очевидно,

β = P (H

= H

) = P (X ∈ V /H

(β равняется вероятности того, что X не принадлежит критической области

V при условии, что верна H

Пример 12.4. При контроле качества продукции возможны ошибки:

изделие, удовлетворяющее стандарту, отбраковывают с вероят-

ностью γ, а бракованное изделие принимают с вероятностью δ.

Если ввести для данного изделия две гипотезы: H

: {изделие

годное} и H

: {изделие бракованное}, и в качестве критерия выбора

использовать контроль продукции, то γ – вероятность ошибки 1-го

рода, а δ – вероятность ошибки 2-го рода данного критерия.

Подумаем, что изменится, если гипотезы являются сложными. Про-

стой гипотезе соответствует единственное распределение, а сложной – мно-

жество распределений. Пусть H

– сложная гипотеза и ей соответствуют

распределения F

, . . . , F

(для параметрической гипотезы F

= F

). Тогда

вероятность

α = P (H

= H

) = P (X ∈ V/H

)

будет зависеть от того, при каком именно из распределений F

, . . . , F

вы-

числяется вероятность.

Если гипотез больше двух, например, имеются гипотезы H

, . . . , H

то говорят, что произошла ошибка i-го рода, если гипотеза H

отвергнута

Некоторые математики, например, А.А. Боровков, называют уровнем значимости величину 1 − α, и это

обоснованно, поскольку α – малое число, а 1 − α, как правило, близка к 1 (чтобы у хорошего критерия

значимость была высокой). Но мы используем традиционную терминологию, в которой уровень значимости

означает ошибку и должен быть низким у хорошего критерия. Из контекста всегда бывает ясно, какой смысл

вкладывает автор в это понятие.

109

критерием, в то время как она верна. Вероятностью ошибки i-го рода назы-

вается число

) = P(H

(X) 6= H

верна) = P

(X) 6= H

При рассмотрении простых параметрических гипотез H

: θ = θ

используют обозначения

α = P (X ∈ V/θ

β = P (X ∈ V /θ

Иногда удобно использовать обозначения α

= α, α

= β.

Ошибки первого и второго рода взаимосвязаны; при попытке умень-

шить одну из ошибок критерия другая, как правило

, увеличивается (рис.

6).

(x)

Z/H

Рис. 6. Ошибки первого (α) и второго (β) рода

Из рис. 6 видно, что если передвигать границу критической области d

вправо, вероятность ошибки первого рода α уменьшается, но зато вероят-

ность ошибки второго рода β увеличивается.

Вероятности этих ошибок можно выразить через функцию мощности

критерия.

Определение 12.8. Функцией мощности критерия K

называется

функция

W (V, θ) = P (X ∈ V ), θ ∈ Θ. (103)

В случае простых гипотез Θ = {θ

, θ

}. Через W (V, θ) легко вычислить

α = P (X ∈ V/θ

) = W (V, θ

) (104)

Как правило, но не всегда.

110