Крупкина Т.В. Математическая статистика
Подождите немного. Документ загружается.

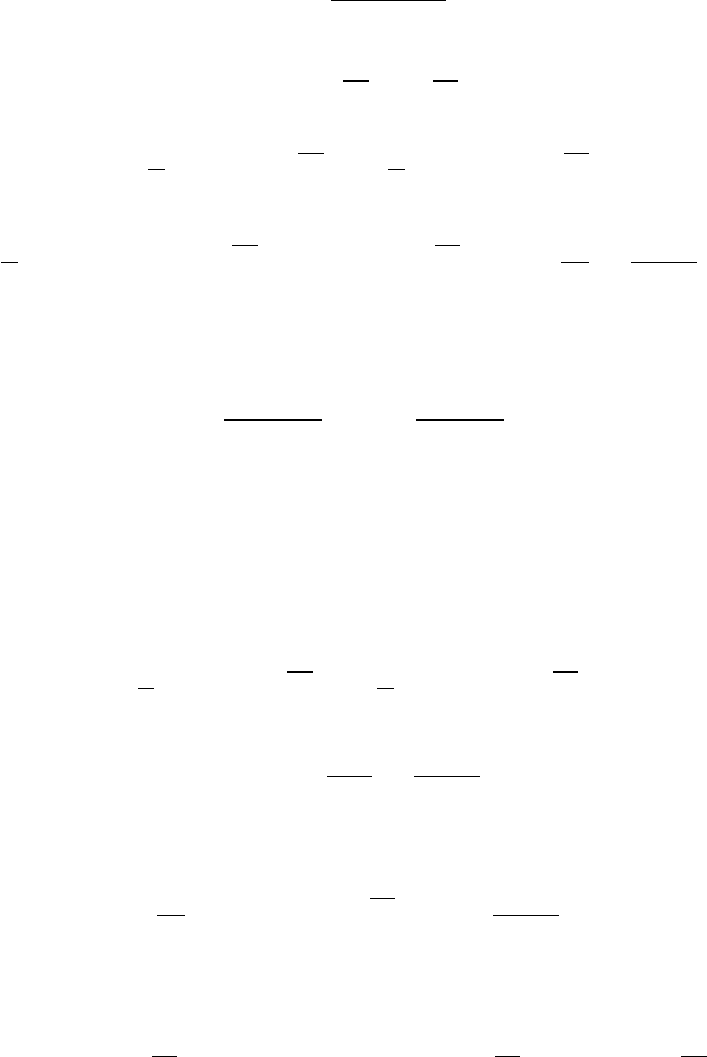
5.
E S
2
=
(n − 1)µ
2
n
. (17)
Доказательство. Сделаем сдвиг величины X на E X (что не изменяет
дисперсии); тогда D X = E X
2
и D X = E X
2
.
S
2
=
1
n
X
X
i
− X
2
=
1
n
X
X
2
i
− X
2
.
E S
2
=
1
n
X
E X
2
i
−E(X
2
) = D X −D X = σ
2
−
σ
2
n
=
n − 1
n
·σ
2
.
6.
D S
2
=
(n − 1)
2
n
3
µ
4
−
(n − 3)
n − 1
µ
2
2
. (18)
Доказательство.
По-прежнему будем делать сдвиг величины X на E X; тогда все цен-
тральные моменты нечетных порядков равны 0. По свойствам выбо-
рочной дисперсии
S
2
=
1
n
X
X
i
− X
2
=
1
n
X
X
2
i
− nX
2
,
E S
2
= µ
2
−
nµ
2
n
2
=
n − 1
n
µ
2
.
Таким образом,
D S
2
=
1
n
2
E
X
X
2
i
− nX
2
2
−
n − 1
n
2
µ
2
2
. (19)
Обозначим
J = E
X
X
2
i
− nX
2
2
= E
X
X
2
i
2
− 2nX
2
X
X
2
i
+ n
2
X
4
=
= E
1
+ E
2
+ E
3
. (20)
1) E
1
= E
X
X
2
i
2
= E
X
X
4
i
+
X
i,j
i6=j
X
2
i
X
2
j
= nµ
4
+ n(n −1)µ
2
2
.
21
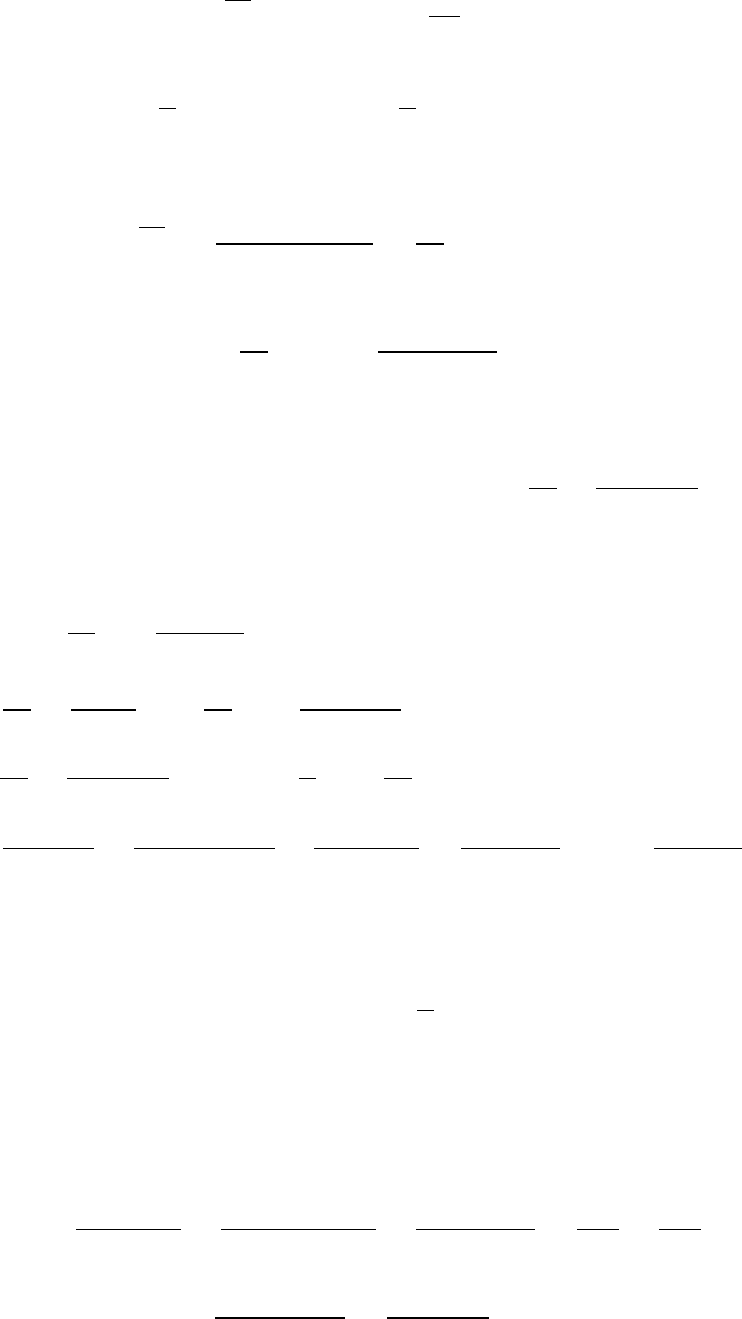
2) E
2
= −2n E
X
2
X
X
2
i
= −
2n
n
2
E
X
X
i
2
X
X
2
i
=
= −
2
n
E
X
X
2
i
2
= −
2
n
nµ
4
+ n(n − 1)µ
2
2
.
3) E
3
= n
2
E X
4
=
n
2
E
P
X
i
4
n
4
=
1
n
2
E
X
X
4
i
+ C
2
4
X
i<j
X
2
i
X
2
j
=
=
1
n
2
nµ
4
+
6n(n − 1)
2
µ
2
2
.
Подставим найденные значения в (21).
J = nµ
4
+ n(n − 1)µ
2
2
− 2µ
4
− 2(n − 1)µ
2
2
+
µ
4
n
+
3(n − 1)
n
µ
2
2
. (21)
Подставляя (21) в (19), окончательно находим:
D S
2
=
J
n
2
−
(n − 1)
n
2
µ
2
2
=
=
µ
4
n
+
n − 1
n
µ
2
2
−
2
n
2
µ
4
−
2(n − 1)
n
2
µ
2
2
+
+
µ
4
n
3
+
3(n − 1)
n
3
µ
2
2
− µ
2
2
+
2
n
µ
2
2
−
1
n
2
µ
2
2
=
=
µ
4
− µ
2
2
n
−
2(µ
4
− 2µ
2
2
)
n
2
+
µ
4
− 3µ
2
2
n
3
=
(n − 1)
2
n
3
µ
4
−
(n − 3)
n − 1
µ
2
2
.
(22)
Таким образом,
D S
2
= O
1
n
.
Следствие. Отсюда легко получить дисперсию S
2
для нормального распре-
деления N(a, σ) :
D S
2
=
3σ
4
− σ
4
n
−
2(3σ
4
− 2σ
4
)
n
2
+
3σ
4
− 3σ
4
n
3
=
2σ
4
n
−
2σ
4
n
2
=
=
2σ
4
(n − 1)
n
2
=
2(n − 1)
n
2
σ
4
.
22

Мы использовали найденные ранее значения моментов нормального рас-
пределения: µ
2
= σ
2
, µ
4
= 3σ
4
, (общая формула: µ
2k
= (2k − 1)!! · σ
2k
).
Часто используется также дисперсия исправленной выборочной дис-
персии. Найдем ее:
D S
2
=
n
2
(n − 1)
2
D S
2
=
2
n − 1
σ
4
. (23)
2.3. Другие характеристики выборки
Определение 2.8. Выборочной модой называется значение
m
o
, чаще всего наблюдающееся:
n
i
(m
0
) = max
i
n
i
.
Определение 2.9. Выборочной медианой называется значе-
ние m
e
, равное среднему члену вариационного ряда:
m
e
= X
∗
[
n
2
]
+1
.
Определение 2.10. Выборочной квантилью порядка q, 0 < q <
1 называется значение X
q
, равное члену вариационного ряда с номе-
ром [nq] + 1.
Вычисление выборочных характеристик связи между величина-
ми X и Y .
Выборочная ковариация K
XY
:
K
XY
= XY − X · Y , где XY =
1
n
P
n
i=1
X
i
Y
i
.
Выборочный коэффициент корреляции r
XY
:
r =
K
XY
s
X
s
Y
.
Выборочное уравнение линейной регрессии Y на X:
ˆ
Y − Y = r
s
Y
s
X
(X − X).
Выборочное уравнение линейной регрессии X на Y :
ˆ
X − X = r
s
X
s
Y
(Y − Y ).
23

2.4. Сходимость выборочных моментов и функций от них
Для практических приложений важное значение имеет вопрос о по-
ведении выборочных характеристик при возрастании объема выборки n.
По аналогии с эмпирической функцией распределения можно ожидать, что
при неограниченном возрастании n выборочные моменты будут сходиться
по вероятности к соответствующим теоретическим моментам. Действитель-
но, пусть случайная величина ξ имеет все моменты α
k
. Соответствующие
им выборочные моменты обозначим a
nk
, чтобы подчеркнуть зависимость от
n. Все a
nk
представляют собой случайные величины и при фиксированном k
для каждого n имеют одинаковые математические ожидания α
k
и дисперсии
α
2k
−α
2
k
n
. Это следует из соотношений
E a
nk
=
1
n
n
X
i=1
E X
k
i
= E ξ
k
= α
k
; (24)
D a
nk
=
1
n
n
X
i=1
D X
k
i
=
1
n
D ξ
k
=
E ξ
2k
− (E ξ
k
)
2
n
=
α
2k
− α
2
k
n
. (25)
Но тогда из закона больших чисел вытекает, что a
nk
сходится по вероят-
ности к α
k
при n → ∞. Поэтому выборочные моменты a
nk
можно исполь-
зовать в качестве приближенных значений для соответствующих теорети-
ческих моментов. Аналогичное утверждение справедливо вообще для лю-
бых непрерывных функций от конечного числа величин. Напомним форму-
лировку соответствующей теоремы.
Теорема 2.1. Пусть ϕ(x
1
, . . . , x
m
) — непрерывная функция. Тогда, ес-
ли последовательность {ξ
kn
} сходится по вероятности к ξ
k
, то
и последовательность {ϕ(ξ
1n
, . . . , ξ
mn
)} сходится по вероятности к
ϕ(ξ
1
, . . . , ξ
m
):
ξ
kn
p
→ ξ
k
⇒ ϕ(ξ
1n
, . . . , ξ
mn
)
p
→ ϕ(ξ
1
, . . . , ξ
m
). (26)
Теорема 2.1 имеет важное значение, поскольку из нее следует, в част-
ности, что любые центральные выборочные моменты, коэффициенты асим-
метрии и эксцесса при неограниченном увеличении объема выборки схо-
дятся по вероятности к соответствующим теоретическим характеристикам.
Действительно, из (14), используя бином Ньютона, можно получить
m
k
=
k
X
l=0
(−1)
l
C
l
k
X
l
a
k−l
, (27)
24
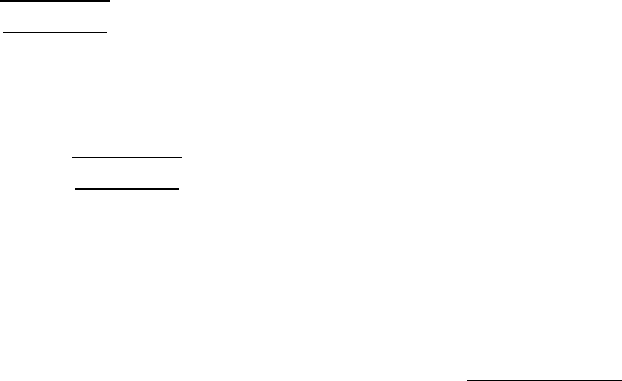
то есть любой центральный выборочный момент можно представить в виде
непрерывной функции от выборочных моментов, которые сходятся по ве-
роятности к теоретическим моментам. С другой стороны, центральные тео-
ретические моменты выражаются через теоретические моменты также по
аналогичной (27) формуле:
µ
k
= E(ξ − E ξ)
k
=
k
X
l=0
(−1)
k−l
C
l
k
α
l
1
α
k−l
. (28)
Таким образом, все условия теоремы 2.1 выполняются. Аналогичные рас-
суждения справедливы для коэффициентов асимметрии и эксцесса.
До сих пор мы рассматривали сходимость выборочных характеристик
к соответствующим теоретическим. Однако важное значение имеет и вопрос
о поведении распределений выборочных характеристик для больших выбо-
рок. Легко видеть, что каждый выборочный момент a
k
представляет собой
сумму n независимых и одинаково распределенных случайных величин, и
поэтому к нему можно применить центральную предельную теорему. В этой
связи приведем теорему.
Теорема 2.2. Распределение выборочного момента a
k
при n → ∞ схо-
дится к нормальному распределению.
Теорема 2.2 означает, что выборочное распределение случайной вели-
чины a
k
при n → ∞ является приближенно нормальным. Последнее обсто-
ятельство позволяет при больших выборках оценить вероятность, с которой
значения выборочного момента отклонятся от теоретического на величину,
не большую ε. Правда, при этом необходимы значения теоретических мо-
ментов. Действительно, для любого ε > 0 при n → ∞ вероятность события
P
r
n
α
2k
− α
2
k
|a
k
− α
k
| < ε
→ 2Φ(ε) − 1,
где Φ(t) – функция распределения закона N(0, 1). Следовательно, вероят-
ность события
r
n
α
2k
− α
2
k
|a
k
− α
k
| < ε
при больших n примерно равна 2Φ(ε)−1. Для центральных выборочных мо-
ментов m
k
при n → ∞также справедливо утверждение о сходимости их вы-
борочных распределений к нормальному (доказательство этого утвержде-
ния можно найти в работе [35]). Например, распределение выборочной дис-
персии S
2
n
сходится к нормальному распределению N(µ
2
,
p
(µ
4
− µ
2
2
)/n).
25

2.5. Контрольные вопросы
1. Дайте определение выборочного среднего.
2. Докажите, что в любом распределении E X = E ξ.
3. Докажите, что D X =
σ
2
n
.
4. Приведите формулу для вычисления выборочного среднего по
статистическому ряду.
5. Приведите формулу для вычисления выборочной дисперсии по
статистическому ряду.
6. Укажите два различных способа найти выборочную дисперсии
по вариационному ряду.
7. Как изменятся выборочные дисперсия и среднее квадратическое
отклонение, если прибавить к каждому элементу выборки по-
стоянную c?
8. Как изменятся выборочные дисперсия и среднее квадратическое
отклонение, если умножить каждый элемент выборки на посто-
янную c?
9. Что характеризует выборочный коэффициент асимметрии?
10. Выразите выборочный центральный момент 3-го порядка через
выборочные начальные моменты.
11. Как называется средний член вариационного ряда?
12. Квантилью какого порядка является медиана?
13. Каково асимптотическое распределение выборочного среднего в
модели Пуассона hP
λ
i?
14. Каково точное распределение выборочного среднего в модели
Пуассона hP
λ
i?
26
Лекция 3. Группировка выборки
Единица – ноль, единица – вздор,
голос единицы – тоньше писка.
В. Маяковский
План лекции: группировка выборки, гистограмма и полигон ча-
стот, пример группировки выборки, поправки Шеппарда.
3.1. Гистограмма и полигон частот
Кроме эмпирической функции распределения существуют и другие
способы наглядного представления и сжатия статистических данных. Од-
ним из таких способов является построение гистограммы.
Пусть нам дана реализация (x
1
, . . . , x
n
) выборки X из F
ξ
. Интер-
вал [x
∗
1
, x
∗
n
] разбивают на подынтервалы [a
0
, a
1
], [a
1
, a
2
], . . . , [a
k−1
, a
k
], где
a
0
= x
∗
1
, a
k
= x
∗
n
. Затем подсчитывают число n
j
координат реализации (эле-
ментов выборки), попавших в каждый подынтервал [a
j−1
, a
j
], j = 1, . . . , k,
то есть подсчитывают частоту попадания статистических данных в каждый
подынтервал. Иначе говоря, данные группируют. На каждом подынтервале,
как на основании, строят прямоугольники площади
n
j
n
, для чего берут высо-
ту прямоугольника равную
n
j
nh
j
, где h
j
– длина j-го подынтервала (на прак-
тике обычно длину каждого подынтервала полагают равной h). Полученную
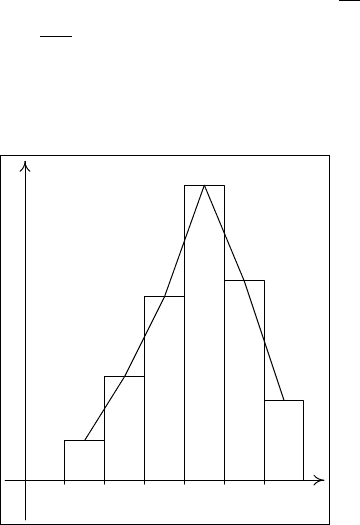
при этом фигуру называют гистограммой (рис. 2).
Y
XO
Рис. 2. Гистограмма и полигон частот
Поскольку площадь каждого прямоугольника есть не что иное, как
относительная частота попадания выборочных значений в соответствую-
27

щий интервал, то по теореме Бернулли она будет сходиться по вероятности
при n → ∞ к вероятности попадания значения случайной величины ξ в со-
ответствующий интервал. Если случайная величина ξ непрерывная и f(x)
ее плотность, то огибающая (верхняя граница) гистограммы является ста-
тистическим аналогом для теоретической плотности f(x).
В методе гистограмм неизвестная плотность распределения прибли-
жается кусочно-постоянными функциями. Но точность приближения мож-
но улучшить, если применить кусочно-линейные функции. Для этой цели
строят полигон частот. Полигон частот – это ломаная линия, проходящая
через середины верхних границ прямоугольников гистограммы. Построен-
ная таким образом кусочно-линейная функция также является статистиче-
ским аналогом теоретической плотности (рис. 2).
Можно построить также кумуляту – ломаную с вершинами в точках
(a
i
;
1
n
P
i−1
j=1
n
j
). Кумулята дает представление о графике функции распреде-
ления, а гистограмма и полигон – о графике плотности распределения.
Еще раз отметим, что интерпретация графических характеристик
как статистических аналогов вероятностных характеристик имеет смысл и
обоснование только для выборки X из непрерывного распределения F .
3.2. Пример группировки выборки
Рассмотрим на примере, как сгруппировать выборку, состоящую из
1000 элементов. Пусть для определенности минимальный элемент выборки
равняется x
min
= 0, 01, а максимальный x
max
= 10, 65.
Определим сначала число интервалов k. Рекомендуется брать k такое,
что 2
k−1
∼ n.
В данном примере n = 1000.
2
10
= 1024 ∼ 1000; k − 1 = 10, k = 11.
Выберем число интервалов k = 11.
2. Определим длину интервала h:
h =
x
max
− x
min
k
.
Находим
h =
10, 65 − 0, 01
11
≈ 0, 967.
3. Найдем границы интервалов группировки x
0
= x
min
, x
i
= x
0
+
hi, i = 1, ..., k и составим таблицу группировки. Внесем границы интер-
валов в столбец «Интервал». Подсчитаем, сколько элементов выборки по-
пало в каждый интервал и заполним в таблице столбец «Численность n
i
».
28
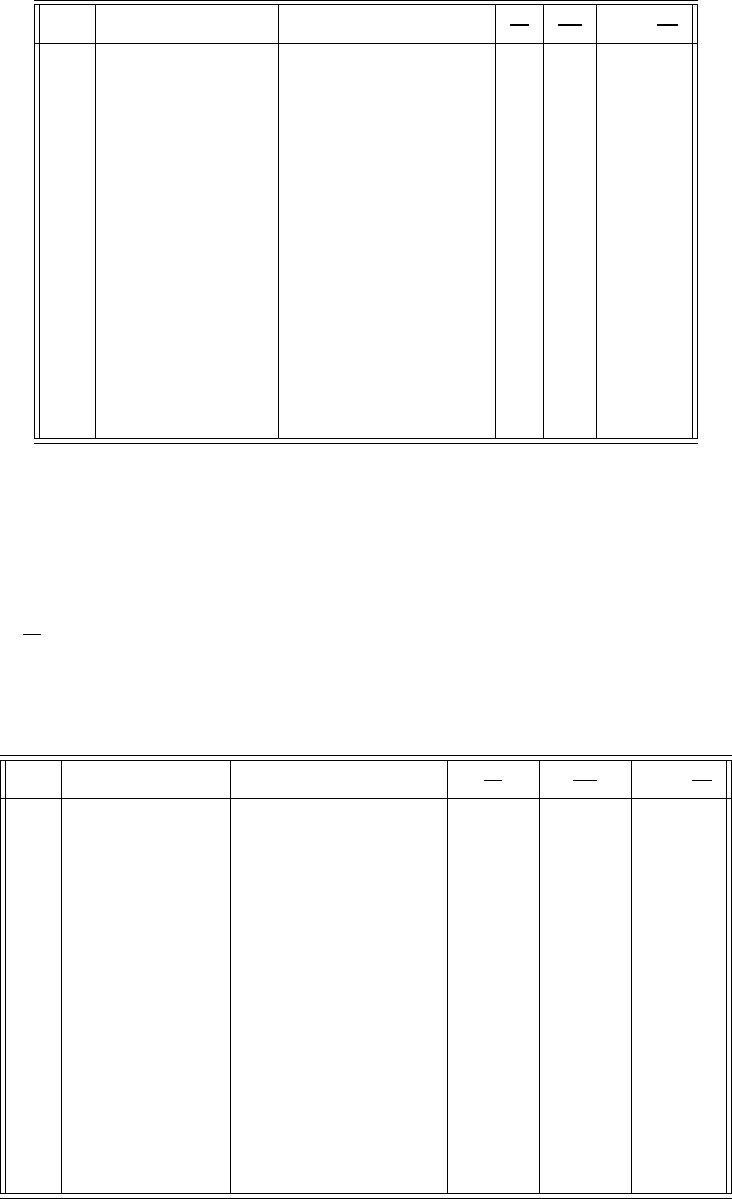
Остальные столбцы рассчитываются по столбцу численностей. Они приго-
дятся при построении графических характеристик.
№ Интервал Численность n
i
n
i
n
n
i
nh
P
i
1
n
j
n
1 0, 01 − 0, 98
2 0, 98 − 1, 94
3 1, 94 − 2, 91
4 2, 91 − 3, 88
5 3, 88 − 4, 85
6 4, 85 − 5, 81
7 5, 81 − 6, 78
8 6, 78 − 7, 75
9 7, 75 − 8, 72
10 8, 72 − 9, 68
11 9, 68 − 10, 65
Ниже показана заполненная таблица. Обратите внимание, что сумма эле-
ментов столбца «Численность n
i
» должна равняться n, а сумма элементов
столбца «
n
i
n
» должна равняться 1.
№ Интервал Численность n
i
n
i
n
n
i
nh
P
i
1
n
j
n
1 0, 00 − 0, 09 80 0,080 0,007 0,080
2 0, 09 − 0, 18 81 0,081 0,007 0,161
3 0, 18 − 0, 27 93 0,093 0,008 0,254
4 0, 27 − 0, 36 85 0,085 0,008 0,339
5 0, 36 − 0, 45 87 0,087 0,008 0,426
6 0, 45 − 0, 54 87 0,087 0,008 0,513
7 0, 54 − 0, 63 87 0,087 0,008 0,600
8 0, 63 − 0, 72 106 0,106 0,010 0,706
9 0, 72 − 0, 81 99 0,099 0,009 0,805
10 0, 81 − 0, 90 89 0,089 0,008 0,894
11 0, 90 − 0, 99 106 0,106 0,010 1,000
29
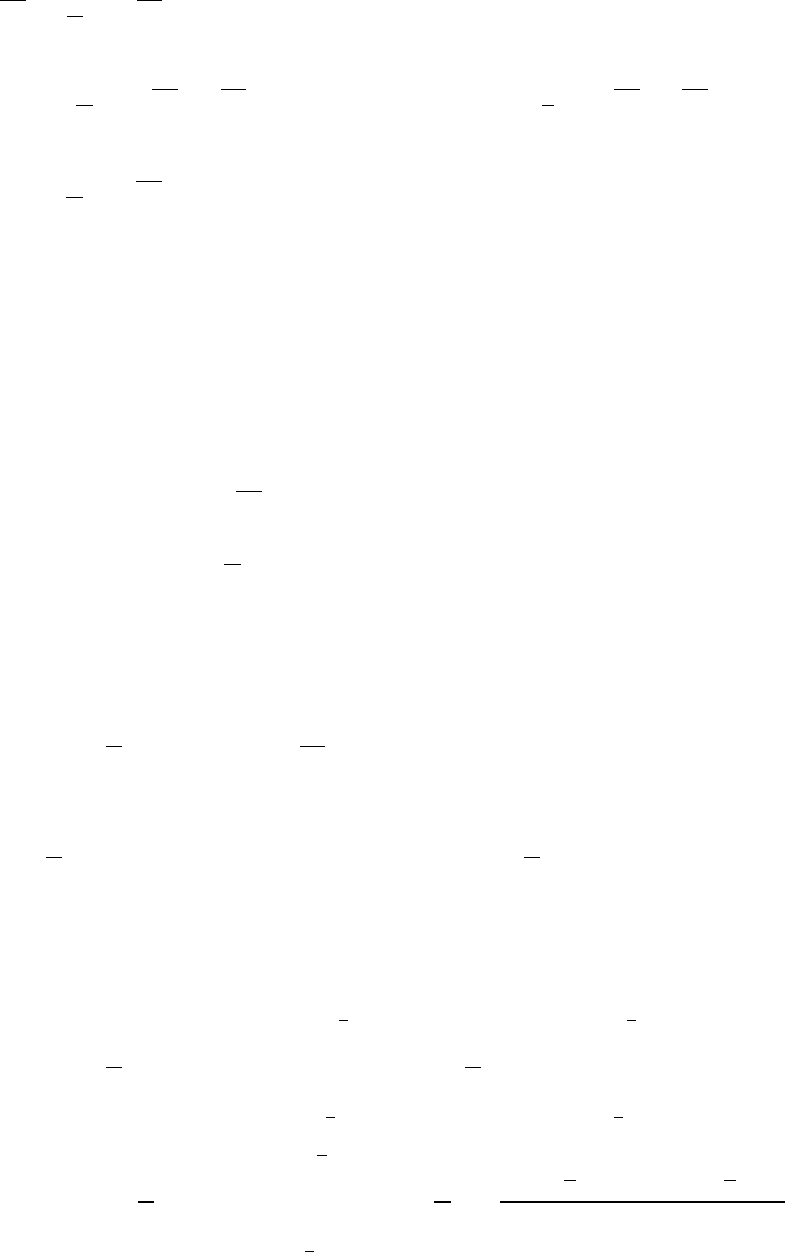
3.3. Поправки Шеппарда
Выборочные моменты можно приближенно найти по формулам
X ≈
1
n
k
X
i=1
X
i
n
i
,
m
s
≈
1
n
k
X
1
(X
i
− X)
s
n
i
, в частности s
2
=
1
n
P
k
1
(X
i
− X)
2
n
i
,
a
s
≈
1
n
k
X
1
X
s
i
n
i
,
где сумми-
рование ведется по всем интервалам. Попробуем оценить погрешность при
использовании этих приближенных формул. Будем считать, что интервалы
охватывают всю числовую ось (n
i
могут быть равными 0).
Пусть δ – случайная точка из отрезка [0, h], примем ее за середину
некоторого интервала, тогда границы этого интервала будут δ − h/2, δ +
h/2; а границы i-го интервала вправо от δ: δ + (i − 1/2)h, δ + (i + 1/2)h.
Эти границы – случайные величины, как функции δ. Середины интервалов
имеют координаты: X
i
= δ + ih.
Имеем ˜a
s
=
1
n
∞
X
i=−∞
n
i
(δ + ih)
s
. Выражение в правой части имеет два
источника случайности: n
i
и δ.
Найдем E ˜a
s
:
E ˜a
s
=
1
h
Z
h
0
dδ
∞
X
−∞
E
n
i
n
(δ + ih)
s
/δ =
=
1
h
Z
h
0
dδ
∞
X
−∞
δ+(i+1/2)h
Z
δ+(i−1/2)h
f(x) dx · (δ + ih)
s
=
1
h
Z
h
0
dδ
∞
X
−∞
(δ + ih)
s
δ+(i+1/2)h
Z
δ+(i−1/2)h
f(x) dx.
Пусть δ + ih = y, тогда
E ˜a
s
=
1
h
∞
X
−∞
(i+1)h
Z
ih
y
s
dy
y+
h
2
Z
y−
h
2
f(x) dx =
1
h
∞
Z
−∞
y
s
dy
y+
h
2
Z
y−
h
2
f(x) dx =
=
1
h
∞
Z
−∞
f(x) dx
x+
h
2
Z
x−
h
2
y
s
dy ==
1
h
∞
Z
−∞
(x +
h
2
)
s+1
− (x −
h
2
)
s+1
s + 1
· f(x) dx.
30
