Крупкина Т.В. Математическая статистика

Подождите немного. Документ загружается.

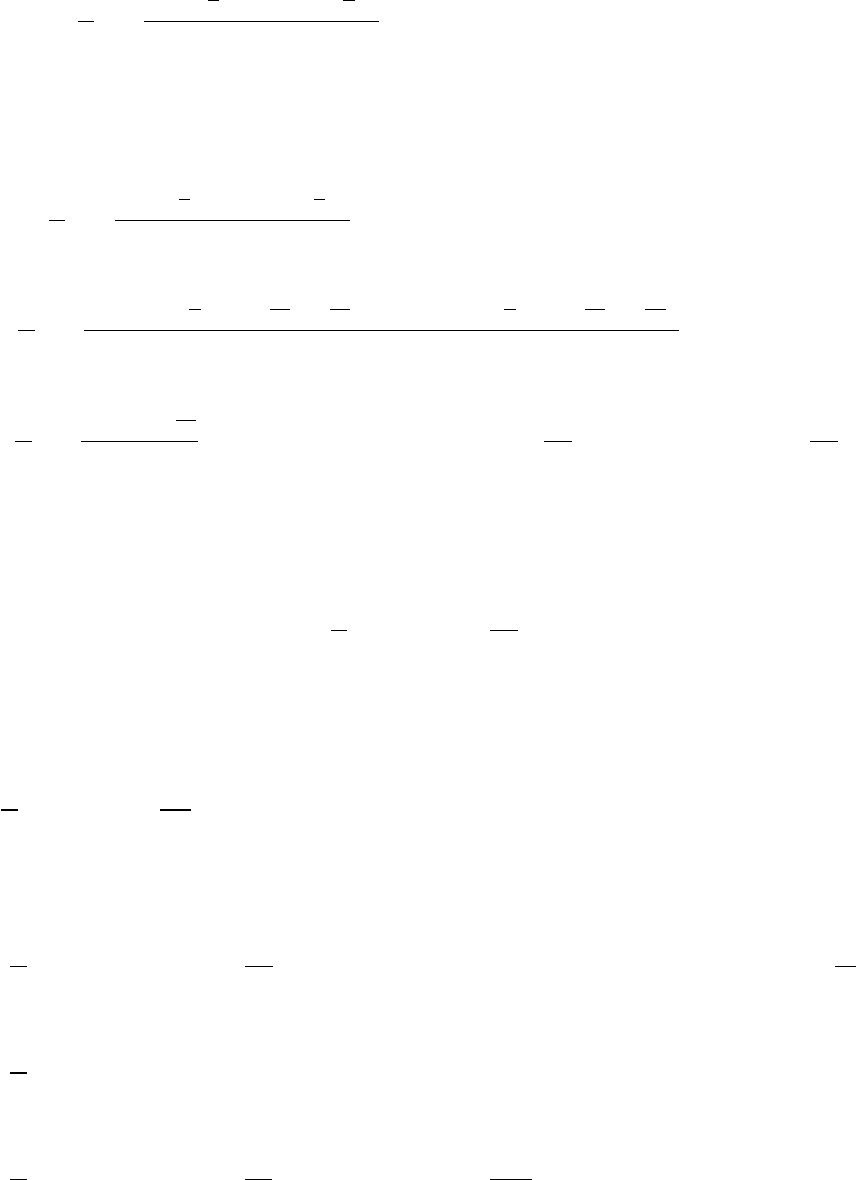
Вычислим E ˜a

E ˜a

∞

−∞

(x +

)

− (x −

)

· f(x) dx =

∞

−∞

xf(x) dx = E ξ = a.

Таким образом, оценка является точной. Далее

E ˜a

∞

−∞

(x +

)

− (x −

)

· f(x) dx =

∞

−∞

+ 3x

− (x

− 3x

+ 3x

−

)

· f(x) dx =

∞

−∞

h +

· f(x) dx =

∞

−∞

f(x) dx +

∞

−∞

f(x) dx = a

Получили более точную оценку для ˜a

≈

i=1

¯x

−

Выпишем еще некоторые формулы:

≈

i=1

¯x

−

¯x

≡ 0,

≈

i=1

(¯x

− ¯x)

−

, (поправка равна −

)

≈

i=1

(¯x

− ¯x)

, (поправки нет)

≈

i=1

(¯x

− ¯x)

−

i=1

(¯x

− ¯x)

240

Применяются также интерполяционные формулы для нахождения

выборочных медианы, квантилей и моды по группированной выборке.

Медианным называется интервал, в котором накопленная сумма ча-

стот впервые достигает

. Выборочной группированной медианой на-

зывается значение m

∗

= x

+ h ·

n/2 − (n

+ . . . + n

−1

)

где n – объем выборки, h – длина интервала группировки, x

– левая гра-

ница медианного интервала, n

– численность i-го интервала, n

– числен-

ность медианного интервала.

Квантильным порядка q интервалом называется интервал, в кото-

ром сумма накопленных частот впервые достигает значения q. Выбороч-

ной группированной квантилью называется значение X

∗

= X

(q)

+ h ·

nq − (n

+ ··· + n

(q)−1

)

(q)

где X

(q)

– левая граница квантильного интервала, n

(q)

– численность кван-

тильного интервала, n

, ··· , n

(q)−1

– численности интервалов, предшеству-

ющих квантильному.

Модальным называется интервал, имеющий наибольшую числен-

ность. Выборочной группированной модой называется значение m

∗

= x

+ h ·

− n

−1

− n

−1

− n

где x

– левая граница модального интервала, n

– численность модаль-

ного интервала, n

−1,

, n

– численности интервалов слева и справа от

модального.

Пример 3.1. Дан группированный статистический ряд величины Х:

X 1 − 5 5 − 9 9 − 13 13 − 17

2 8 9 1

Найти приближенно квантиль порядка 0, 4.

J Квантильным интервалом является второй, так как в этом интервале сум-

ма накопленных частот впервые достигает значения 0, 4. Его левая граница

0,4

= 5.

∗

0,4

= 5 + 4 ·

20 · 0, 4 − 2

= 8.

3.4. Контрольные вопросы

1. Каким образом при группировке выборки можно найти опти-

мальное число интервалов?

2. Каким образом при группировке выборки рассчитывается длина

интервала?

3. Какие графические характеристики выборки дают представле-

ние о графике плотности?

4. Какие графические характеристики выборки дают представле-

ние о графике функции распределения?

5. Чему равняется площадь под гистограммой частот?

6. Можно ли восстановить по гистограмме относительных ча-

стот вариационный ряд?

7. Можно ли восстановить по гистограмме частот группирован-

ный ряд?

8. Дайте определение медианного интервала.

9. Дайте определение модального интервала.

10. Дайте определение квантильного интервала порядка 0,3.

11. Что уточняют поправки Шеппарда?

12. Чему равна поправка Шеппарда для группированного первого

начального момента?

13. Чему равна поправка Шеппарда для группированного второго

начального момента?

14. Как изменится поправка Шеппарда для группированного вто-

рого начального момента при увеличении длины интервала

группировки?

Лекция 4. Важные распределения математической статистики

Мы встретимся еще с одним значением слова «статистика»

– так называют функцию от элементов выборки из

некоторой генеральной совокупности.

М. Кендалл, А. Стюарт «Теория распределений»

План лекции: распределение хи-квадрат, распределение Стью-

дента, распределение Фишера, теорема Фишера, теоремы о рас-

пределении выборочных характеристик.

Рассмотрим некоторые функции от выборки X = (X

, . . . , X

) из нор-

мального распределения, которые играют важную роль в математической

статистике. Для данных функций (статистик) удается получить в явном ви-

де их функции распределения и плотности вероятностей. Вообще говоря,

задача о распределении вероятностей для случайной функции от выборки

X = (X

, . . . , X

) в конечном виде решается крайне редко и функции от

выборки из нормального распределения составляют приятное исключение.

Нормальное распределение часто используют в прикладных исследовани-

ях при построении математической модели изучаемого явления. Теоретиче-

ским обоснованием данного факта может служить центральная предельная

теорема. Любую характеристику изучаемого явления, которая представима

в виде суммы значительного числа случайных одинаково распределенных

факторов, можно приблизительно считать случайной величиной с нормаль-

ным законом распределения. О роли нормального распределения в стати-

стике хорошо и подробно написано в работах [16, 33].

Прежде чем рассматривать распределения функций от выборки из

нормальной генеральной совокупности, введем определения распределений

для трех специальных функций от нормальных случайных величин.

4.1. Распределения хи-квадрат, Стьюдента, Фишера

1. Распределение хи-квадрат (χ

Среди гамма-распределений Γ

α,β

выделяют особый класс, который

часто используют в статистических исследованиях.

Определение 4.1. Гамма-распределение с параметрами α =

, β =

называется распределением хи-квадрат с n степенями свободы и

обозначается χ

Соответствующая случайная величина обозначается тем же символом χ

, а

ее плотность имеет вид

(x) =

−1

Γ(

)

−

, x > 0. (29)

На рис. 3 изображены графики плотности распределения хи-квадрат

при некоторых значениях n.

O X

(x)

Рис. 3. Плотность распределения χ

при разных значениях параметра n

При увеличении числа степеней свободы график плотности становит-

ся все ближе к симметричному.

Свойства распределения хи-квадрат

1. Характеристическая функция ϕ

(t) = (1 − 2it)

−n/2

Доказательство. Для гамма-распределения Γ

α, β

с функцией плотно-

сти

(x) =

Γ (β)

−αx

β−1

при x > 0,

где Γ(β) – гамма-функция, определяемая для всех β > 0 соотношени-

ем

Γ(β) =

∞

β−1

−t

dt,

характеристическая функция, как известно, равна ϕ

(t) =



α−it



Подставляя значения параметров α =

, β =

, получим

(t) =



1 − 2it



n/2

= (1 − 2it)

−n/2

. 

2. E χ

= n, D χ

= 2n.

Доказательство. Из общих формул для распределения Γ

α, β

(E ξ =

, D ξ =

) получаем E χ

= n, D χ

= 2n. 

3. При n > 2 распределение χ

имеет моду m

= n − 2.

Доказательство. Достаточно проверить, что в этой точке достигается

максимум плотности распределения. 

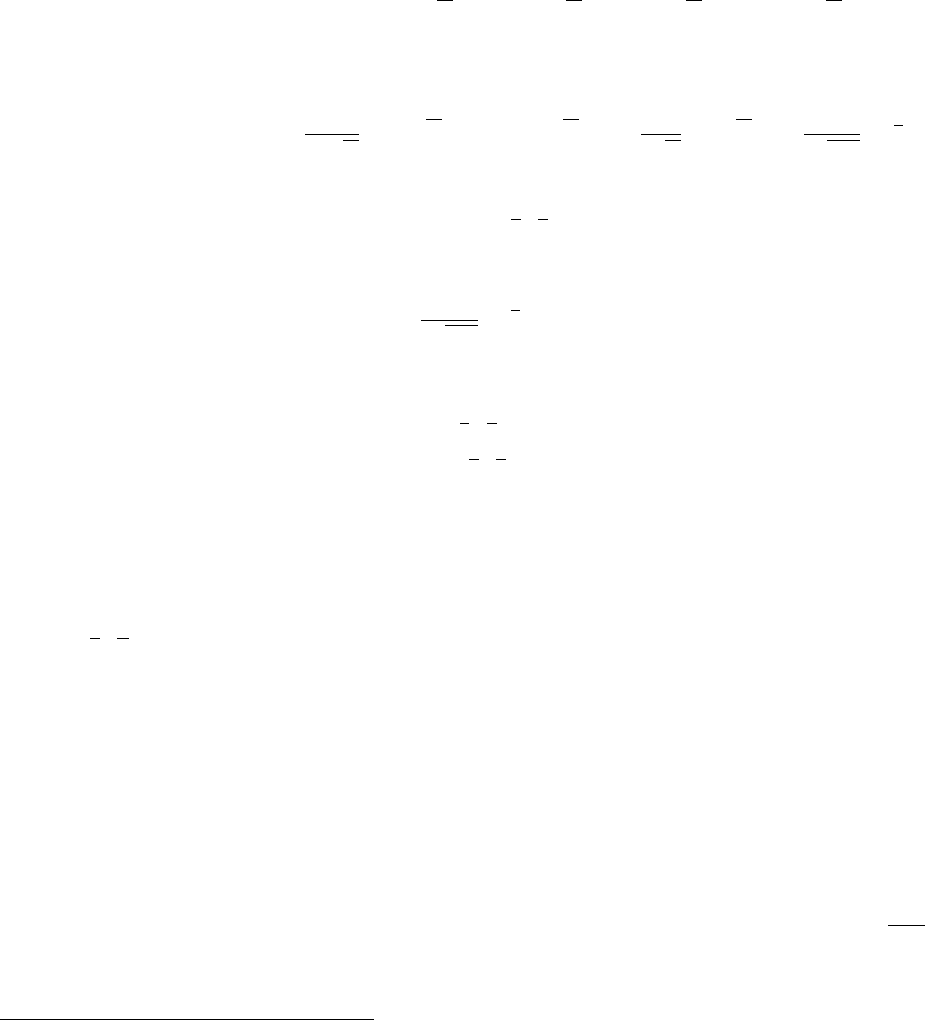
4. Сумма квадратов независимых случайных величин, распределенных по

закону N(0, 1), распределена по закону хи-квадрат с числом степеней

свободы, равным числу слагаемых, то есть

i=1

= χ

Доказательство. Пусть ξ – случайная величина с распределением

N(0, 1). Найдем распределение случайной величины ξ

. Легко видеть,

что для x 6 0 функция распределения равна нулю, а для x > 0

(x) = P (ξ

< x) = P (−

√

x 6 ξ <

√

x) = Φ(

√

x) − Φ(−

√

x), (30)

где Φ(x) – функция стандартного нормального распределения.

(x) = F

(x) =

√

(ϕ(

√

x) + ϕ(−

√

x)) =

√

ϕ(

√

x) =

√

πx

−

(31)

Если рассмотреть распределение Γ(

), то получим следующую фор-

мулу для ее плотности:

f(x) =

√

πx

−

, x > 0. (32)

Сравнивая (32) с плотностью в (31), получаем, что случайная вели-

чина ξ

имеет распределение Γ(

). Таким образом, случайная вели-

чина ξ

имеет распределение Γ(

) с характеристической функцией

(1 − 2it)

−1/2

, а сумма квадратов n независимых случайных величин,

распределенных по нормальному закону N(0, 1), имеет характеристи-

ческую функцию, равную произведению характеристических функций

слагаемых

, то есть (1 − 2it)

−n/2

, что соответствует распределению

Γ(

) = χ

. 

5. Сумма независимых случайных величин, распределенных по закону

хи-квадрат, распределена также по закону хи-квадрат с числом сте-

пеней свободы, равным сумме степеней свободы слагаемых, то есть

+ χ

= χ

n+m

. (33)

Доказательство. Характеристическая функция суммы

+χ

(t) = ϕ

(t)·ϕ

(t) = (1−2it)

−n/2

·(1 −2it)

−m/2

= (1−2it)

−

n+m

а это характеристическая функция χ

n+m

. 

Можно просто вспомнить о суммируемости гамма-распределения.

− n

√

∼ N(0, 1).

Доказательство.

− n

√

i=1

− n

√

величины ξ

независимы и имеют одинаковое распределение Γ(

) с

математическим ожиданием 1 и дисперсией 2. Поэтому E



i=1



n, D



i=1



= 2n и по ЦПТ

i=1

− n

√

−→ u ∈ N(0, 1). 

−→ ξ ≡ 1 (вырожденное в точке 1 распределение).

Доказательство. Пусть ξ

, . . . , ξ

независимы и имеют стандартное

нормальное распределение. Тогда E ξ

= D ξ = 1, и по ЗБЧ

+ . . . + ξ

−→ 1. 

Пример 4.1. Используя свойства распределения χ

, найдем D S

в N(a, σ).

= χ

n−1

, S

n−1

· σ

, D S

D χ

n−1

· σ

2(n − 1)σ

. (34)

n−1

· σ

(n − 1)

, D

D χ

n−1

· σ

(n − 1)

2(n − 1)σ

(n − 1)

n − 1

. (35)

2. Распределение Стьюдента.

Рассмотрим последовательность независимых случайных величин

ξ, ξ

, . . . , ξ

, распределенных по нормальному закону N(0, 1).

Определение 4.2. Распределением Стьюдента T

с n степенями

свободы называется распределение случайной величины

i=1

. (36)

Можно случайную величину t определить как отношение

где χ

– случайная величина, независимая от ξ и распределенная по закону

. Очевидно, что оба определения эквивалентны.

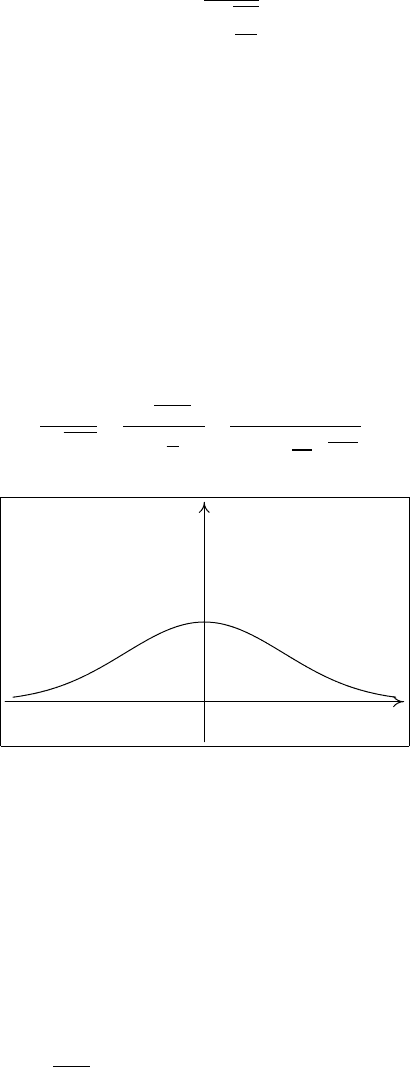
Плотность распределения Стьюдента f

(x) (рис. 4) нетрудно найти с

помощью метода вычисления плотности распределения частного двух неза-

висимых величин (см. соответствующую задачу в § 4 практикума по реше-

нию задач).

Приведем окончательную формулу для плотности распределения

Стьюдента:

(x) =

√

πn

Γ(

n+1

)

Γ(

)

(1 +

)

n+1

, x ∈ R. (37)

(x)

Рис. 4. Плотность распределения Стьюдента f

(x)

Свойства распределения Стьюдента (см. задачи § 5 практикума по

решению задач).

1. Распределение Стьюдента симметрично.

2. E T

= 0, D T



n−2

при n > 2,

∞ при n 6 2.

3. t

−→ u ∈ N(0, 1)

4. У распределения Стьюдента T

существуют только моменты порядков

меньших n, при этом все существующие моменты нечетного порядка

m = 2k + 1 равны нулю.

Замечание 4.1. При n = 1 распределение Стьюдента совпадает с

распределением Коши.

Замечание 4.2. Распределение Стьюдента можно рассматривать

при n ∈ R

3. Распределение Фишера – Снедекора

Рассмотрим две независимые случайные величины χ

и χ

, имеющие

хи-квадрат распределение с n и m степенями свободы соответственно.

Определение 4.3. Распределением Фишера – Снедекора (F -

распределением или распределением дисперсионного отношения

Фишера) с n, m степенями свободы называется распределение слу-

чайной величины

n,m

. (38)

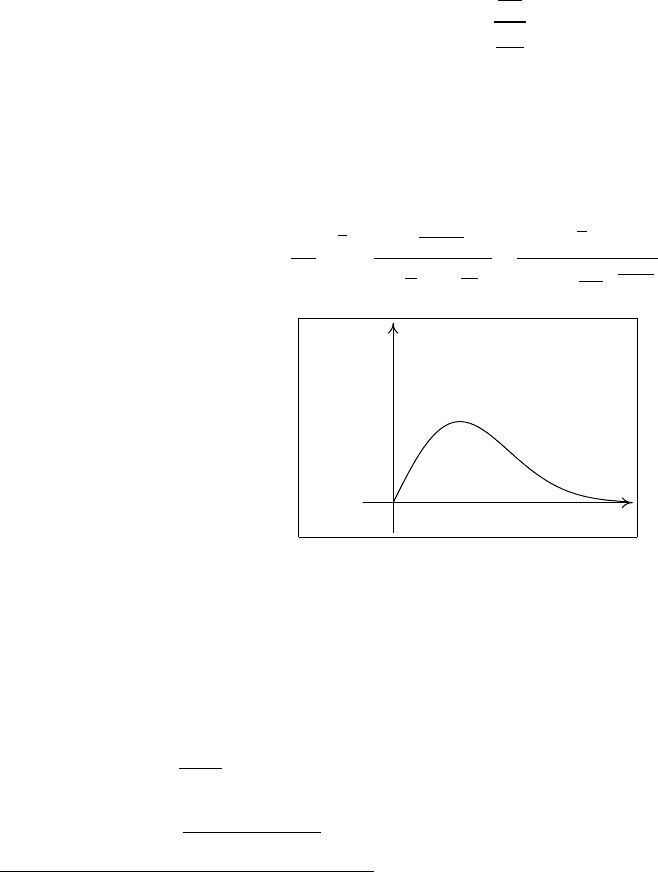
Функцию и плотность распределения F

n,m

(x) (рис. 5) можно найти,

используя тот же способ, что и для распределения Стьюдента. Окончатель-

но формулу для расчета плотности распределения Снедекора записывают в

виде

n,m

(x) =





Γ(

n+m

)

Γ(

)Γ(

)

−1

(1 +

)

n+m

, x ∈ R

. (39)

n,m

(x)

Рис. 5. Плотность распределения Фишера f

n,m

(x)

Из свойств распределения Фишера отметим следующие (см. сответ-

ствующие задачи § 5 практикума по решению задач).

1. E F

n,m

m−2

при m > 2.

2. D F

n,m

(n+m−2)

n(m−2)

(m−4)

при m > 4.

Джордж Уоддел Снедекор (англ. George Waddel Snedecor; 1881–1974) – американский математик и

статистик, ученик Рональда Фишера.

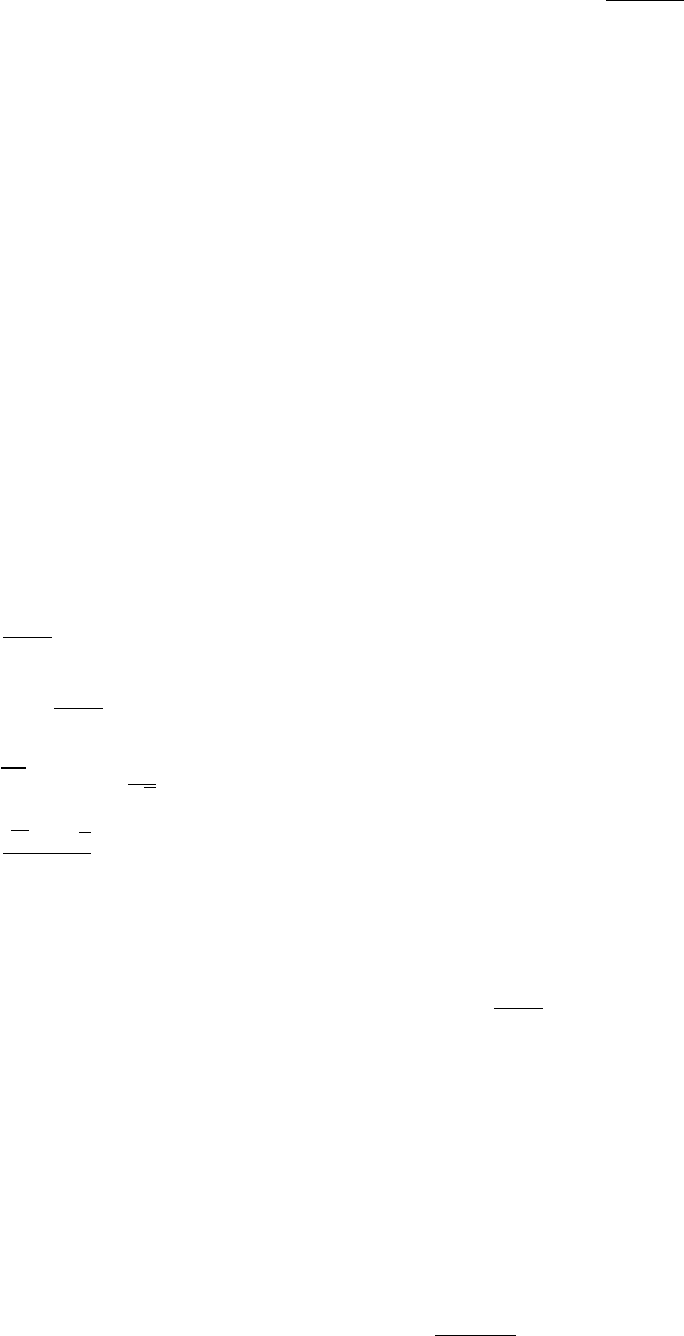
3. При n > 2 распределение F

n,m

имеет моду m

(n−m)m

n(m+2)

4. При n → ∞, m → ∞ f

n,m

−→ ξ ≡ 1 (вырожденное в точке 1 распреде-

ление).

5. Если f

n,m

имеет распределение Фишера F

n,m

, то 1/f

n,m

имеет распре-

деление Фишера F

m,n

Выясним распределение выборочных характеристик нормальной вы-

борки.

4.2. Теорема Фишера

Легко видеть, какое распределение имеет выборочное среднее, най-

денное по выборке из совокупности с нормальным распределением N(a, σ).

Теорема 4.1. Пусть X

, . . . , X

– выборка из распределения N(a, σ).

Тогда:

−a

∈ N(0; 1);

i=1



−a



∈ χ

;

3. X ∈ N(a,

√

);

(X−a)

√

∈ N(0, 1).

Доказательство.

1. Нормальное распределение инвариантно относительно линейного пре-

образования, поэтому величина u

−a

нормально распределена;

параметры этого распределения находятся как математическое ожи-

дание и корень из дисперсии u

, очевидно, они равны соответственно 0

и 1.

2. По свойству 4 распределения χ

сумма квадратов независимых слу-

чайных величин, распределенных по закону N(0, 1), распределена по

закону хи-квадрат с числом степеней свободы, равным числу слагае-

мых, то есть

i=1



− a



∈ χ