Кумыкова С.К., Нахушева Ф.Б. Математика: Практикум по аналитической геометрии и алгебре
Подождите немного. Документ загружается.


11
∆ Пусть угловой коэффициент одной из искомых прямых равен
k
.
Угловой коэффициент заданной прямой равен –2. Так как угол между этими
прямыми равен
4/
p
, то
,
k21
2k
4
tg
-
+
=
p
т.е.
,
k21
2k
1
-
+
= откуда 1
k
2
1
2k
=
-
+
и 1
k
2
1
2k
-=
-
+
.
Решая каждое из полученных уравнений, находим
3/1k
-
=
и
3k
=
.
Итак, уравнение одной из искомых прямых запишется в виде
),
5
x
)(
3
/
1
(
1
y
-
-
=
-
т.е.
,
0
8
y
3
x
=
-
+
а уравнение другой прямой – в виде
),
5
x
(
3
1
y
-
=
-
т.е.
.
0
14
y
x
3
=
-
-
▲
Кривые второго порядка
Окружность. Окружность – это множество точек плоскости, равно-
удаленных от данной точки (центра). Если r – радиус окружности, а точка
С(a;b) – ее центр, то уравнение окружности имеет вид
(
)
(
)
.rbyax
2
22
=-+-
В частности, если центр окружности совпадает с началом координат,
то последнее уравнение примет вид .
222
ryx =+
Эллипс. Эллипсом называется множество точек плоскости, сумма
расстояний которых до двух данных точек, называемых фокусами, есть вели-
чина постоянная (ее обозначают 2а), причем эта постоянная больше расстоя-
ния между фокусами.
Если фокусы эллипса находятся на оси Ох на равных расстояниях от
начала координат в точках
(
)
0;cF
1
и
(
)
,0;cF
2
- то получится каноническое
уравнение эллипса: .1
b
y
a
x
2
2
2
2
=+
Здесь а – большая, b – малая полуось эллипса, причем a, b и с (с – по-
ловина расстояния между фокусами) связаны соотношением .cba
222
+=
Форма эллипса (мера его сжатия) характеризуется его эксцентрисите-
том
a/c=
e
(так как
,
a
c
<
то
1
<
e
).
Расстояния до некоторой точки эллипса М от его фокусов называются
фокальными радиусами-векторами этой точки: .xar,xar
21
ee
+=-= Дирек-
трисами эллипса называют прямые, уравнения которых
.
a
x
e
±=
Гипербола. Гиперболой называется множество точек плоскости, аб-
солютная величина разности расстояний которых до двух данных точек, на-
зываемых фокусами, есть величина постоянная (ее обозначают 2а), причем
эта постоянная меньше расстояния между фокусами. Если поместить фокусы

12
гиперболы в точках
(
)
0;cF
1
и
(
)
0;cF
2
- , то получится каноническое уравне-
ние гиперболы
,1
b
y
a
x
2
2
2
2
=-
где .acb
222
-= Гипербола состоит из двух ветвей и расположена симмет-
рично относительно осей координат. Точки
(
)
0;aA
1
и
(
)
0;aA
2
- назы-
ваются вершинами гиперболы. Отрезок А
1
А
2
такой, что
,a2AA
21
= на-
зывается действительной осью гиперболы, а отрезок В
1
В
2
такой, что
,b2BB
21
= – мнимой осью. Гипербола имеет две асимптоты, уравнения
которых .x)a/b(y ±=
Отношение
1a/c >=
e
называется эксцентриситетом гиперболы.
Фокальные радиусы-векторы правой ветви гиперболы:
axr -=
e
1
(пра-
вый фокальный радиус-вектор),
axr +=
e
2
(левый фокальный радиус-вектор).
Фокальные радиусы-векторы левой ветви гиперболы: axr +-=
e
1
(правый
фокальный радиус-вектор), axr
2
--=
e
(левый фокальный радиус-вектор).
Парабола. Параболой называется множество точек плоскости, равно-
удаленных от данной точки, называемой фокусом, и данной прямой, назы-
ваемой директрисой. Если директрисой параболы является прямая
,
2
/
p
x
-
=
а фокусом – точка
),
0
:
2
/
p
(
F
то уравнение параболы имеет вид
.pxy 2
2
=
(20)
Эта парабола расположена симметрично относительно оси абсцисс.
Уравнение
pyx 2
2
= (21)
является уравнением параболы, симметричной относительно оси ординат.
При p > 0 параболы (20) и (21) обращены в положительную сторону соответ-
ствующей оси, а при p < 0 – в отрицательную сторону.
Длина фокального радиуса-вектора параболы pxy 2
2
= определяется
по формуле
).
0
p
(
2
/
p
x
r
>
+
=
17. Составить уравнение окружности, проходящей через точки А(5;0)
и В (1; 4), если ее центр лежит на прямой х + у – 3 =0.
∆ Найдем координаты точки М – середины хорды АВ; имеем
,32/)15(x
M
=+= ,/)(y
M
2204 =+= т.е. М (3; 2). Центр окружности ле-
жит на серединном перпендикуляре к отрезку АВ. Уравнение прямой АВ
имеет вид
),51/()5x()04/()0y( --=-- т.е.
.
0
5
y
x
=
-
+

13
Так как угловой коэффициент этой прямой есть –1, то угловой коэф-
фициент перпендикуляра к ней равен 1, а уравнение этого перпендикуляра
,
3
x
2
y
-
=
-
т.е.
.
0
1
y
x
=
-
-
Очевидно, что центр окружности С есть точка пересечения прямой АВ
с указанным перпендикуляром, т.е. координаты центра определяются путем
решения системы уравнений
.01yx,05yx
=
-
-
=
-
+
Следовательно,
,
y
,
x
12
=
=
т.е. С (2; 1). Радиус окружности равен длине отрезка СА, т.е.
.)()(r 100125
22
=-+-= Итак, искомое уравнение имеет вид
.10)1y()2x(
22
=-+- ▲
18. Написать уравнения касательных к окружности
,yxyx 0284
22
=+-++ проходящих через начало координат.
∆ Уравнение касательной ищем в виде kxy
=
. Чтобы найти точку пе-
ресечения прямой и окружности, необходимо решить систему уравнений:
kxy,02y8x4yx
22
==+-++ .
Отсюда .x)k(x)k( 02841
22
=+-++ Это уравнение будет иметь рав-
ные корни, если дискриминант его равен нулю, т.е. 0)k1(8)k84(
22
=+--
или .01k8k7
2
=+- Откуда
7
1
k,1k
21
== . Следовательно, уравнения иско-
мых касательных запишутся в виде
.x
7
1
y,xy ==
▲
19. На эллипсе 400y25x16
22
=+ найти точку, расстояние которой от
правого фокуса в четыре раза меньше расстояния от левого фокуса.
∆ Разделив обе части уравнения на 400, находим
,
yx
1
16
25
22
=+ откуда
,a 25
2
= .e,c,c,b,a,b
5
3
3916254516
22
===-==== Расстояния до фо-
кусов
.x
5
3
5r,x
5
3
5r
21
-=+=
По условию .r4r
21
= Следовательно,
.xx
÷
ø
ö
ç
è
æ
-=+
5
3
54
5
3
5 Откуда х = 5. Подставляя это значение в уравнение эл-
липса, получим
.
0
y
=
Искомая точка ).0;5(M ▲
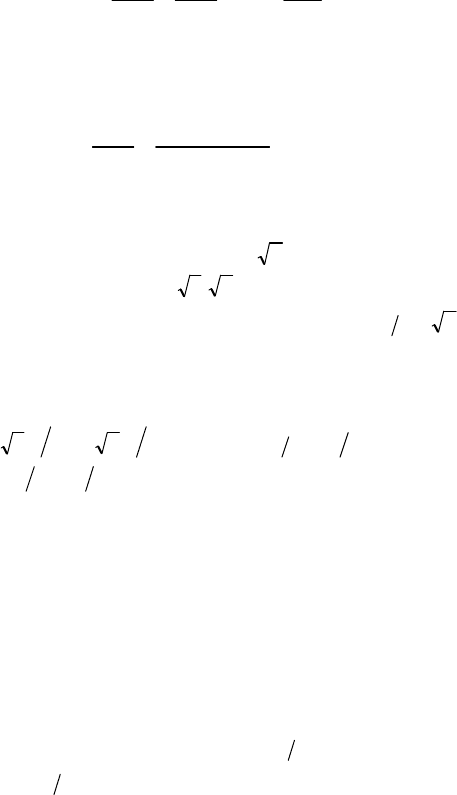
14
20. Даны точки А (-1; 0) и В (2; 0). Точка М(х; у) движется так, что в
треугольнике АМВ угол В остается вдвое больше угла А. Найти уравнение
кривой, которую опишет точка М.
∆ Выразим tg B и tg A через координаты точек А, В и М:
.
x
y
Atg,
x
y
x
y
Btg
1
2
2
+
=
-
=
-
-=
Согласно условию задачи, получаем уравнение
,
A
tg
B
tg
2
=
т.е.
).Atg/(AtgBtg
2
12 -= Подставив в это равенство найденные для
B
tg
и
Atg выражения, приходим к уравнению
;
)x(y
)x/(y
x
y
22
11
12
2
+-
+
=
-
после сокращения на у
(
)
0y ¹ и упрощения получаем ./yx 13
22
=-
Искомая кривая – гипербола. ▲
21. Эксцентриситет гиперболы равен
2 . Составить уравнение ги-
перболы, проходящей через точку
(
)
23,M .
∆ Согласно определению эксцентриситета, имеем 2ac = , или
22
a2c = . Но
222
bac += ; следовательно, а
2
+b
2
=2а
2
или
22
ba = , т.е.
гипербола равнобочная .
Другое равенство получим из условия нахождения точки
M
на ги-
перболе, т.е.
(
)
(
)
123
2
2
2
2
=- ba или
1b2a3
2
2
=- . Поскольку
22
ba = , получим 1a2a3
22
=- , т.е. 1a
2
= .
Таким образом, уравнение искомой гиперболы имеет вид
1yx
22
=- .▲
22. Составить уравнение параболы, симметричной относительно оси
OX
, с вершиной в начале координат, если длина некоторой хорды этой па-
раболы, перпендикулярной оси
OX
, равна 16, а расстояние этой хорды от
вершины равно 6 .
∆ Так как известны длина хорды и расстояние её от вершины, то , сле-
довательно , известны координаты конца этой хорды – точки
M
, лежащей
на параболе . Уравнение параболы имеет вид px2y
2
= ; полагая в нём
8
y
,
6
x
=
=
, находим 6p28
2
×= , откуда 332p2 = . Итак, уравнение иско-
мой параболы 3x32y
2
= .▲

15
23. Составить уравнение параболы с вершиной в начале координат,
симметричной относительно оси
OY
и отсекающей на биссектрисе 1 и 3 ко-
ординатных углов хорду длиной
28 .
∆ Искомое уравнение параболы py2x
2
= , уравнение биссектрисы
x
y
=
. Таким образом, получаем точки пересечения параболы с биссектри-
сой:
(
)
0;0O и
(
)
p2;p2M . Длина хорды определяется как расстояние между
двумя точками:
22
p4p428 += , откуда
8
p
2
=
. Следовательно, искомое
уравнение имеет вид y8x
2
= .▲
Аналитическая геометрия в пространстве
Плоскость
Нормальным уравнением плоскости называется уравнение вида
,
0
p
cos
z
cos
y
cos
x
=
-
+
+
g
b
a
(1)
где
-
g
b
a
cos
,
cos
,
cos
направляющие косинусы перпендикуляра, опущенно-
го из начала координат на данную плоскость, а р – его длина.
Уравнение всякой плоскости может быть записано также в виде
,
0
D
Cz
y
B
Ax
=
+
+
+
(2)
если А
2
+ В
2
+ С
2
0
¹
(общее уравнение). Здесь А, В, С можно рассматривать
как координаты некоторого вектора
CkBjAiN ++= , перпендикулярного
плоскости (нормального вектора плоскости). Для приведения общего урав-
нения плоскости к нормальному виду надо все члены уравнения умножить
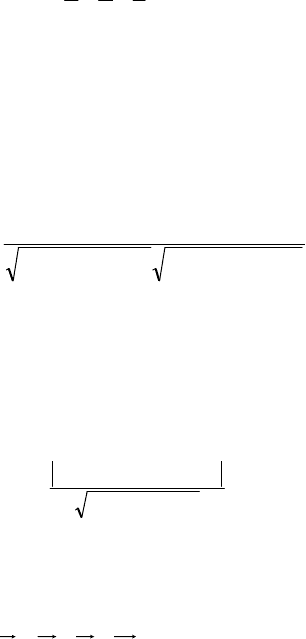
на нормирующий множитель
,CBA/1
222
++±=
m
(3)
где знак перед радикалом противоположен знаку свободного члена D в об-
щем уравнении плоскости.
Частные случаи расположения плоскости, определяемой общим урав-
нением
:
D
Cz
y
B
Ax
0
=
+
+
+
0A
=
; параллельна оси
;
Ox
0B
=
; параллельна оси ;Oy
0C
=
; парал-
лельна оси
;
Oz
0D
=
; проходит через начало координат;
0BA
=
=
; перпенди-
кулярна оси
Oz
(параллельна плоскости
xOy
);
0CA
=
=
; перпендикулярна оси
Oy
(параллельна плоскости
xOz
);
0CB
=
=
; перпендикулярна оси
Ox
(парал-
лельна плоскости
yOz
);
0DA
=
=
; проходит через ось
Ox
;
0DB
=
=
; прохо-
дит через ось
Oy
;
0DC
=
=
; проходит через ось
Oz
;
0DBA
=
=
=
; совпада-
16
ет с плоскостью
xOy
);0z( =
0
=
=
=
DCA
; совпадает с плоскостью
xOz
);
0
y
(
=
0DCB
=
=
=
; совпадает с плоскостью
yOz
)
0
x
(
=
.
Если в общем уравнении плоскости коэффициент
,
0
D
¹
то разделив
все члены уравнения на
,
D
-
уравнение плоскости можно привести к виду
1
c
z
b
y
a
x
=++ (4)
(здесь C/Dc,B/Db,A/Da -=-=-= ). Это уравнение называется уравне-
нием плоскости в отрезках: в нем a, b и c – соответственно абсцисса,
ордината и аппликата точек пересечения плоскости с осями
Ox
,
Oy
,
Oz
.
Угол
j
между плоскостями
0DzCyBxA
1111
=+++
и
0DzCyBxA
2222
=+++ определяется по формуле
.
CBACBA
CCBBAA
cos
2
2
2
2
2
2
2
1
2
1
2
1
212121
++++
++
=
j
(5)
Условие параллельности плоскостей:
.C/CB/BA/A
212121
== (6)
Условие перпендикулярности плоскостей:
.0CCBBAA
212121
=++ (7)
Расстояние от точки
(
)
0000
z;y;xM до плоскости, определяемой
уравнением
,
0
D
Cz
y
B
Ax
=
+
+
+
находится по формуле
,
CBA
DCzByAx
d
222
000
++
+++
= (8)
где берется знак “плюс”, если точка
0
M и начало координат расположены по
разные стороны от плоскости, и “минус”, если они расположены по
одну сторону от плоскости.
Уравнение плоскости, проходящей через точку
(
)
0000
z;y;xM и пер-
пендикулярной вектору
CkBjAiN ++= имеет вид
.0)zz(C)yy(B)xx(A
000
=-+-+- (9)
При произвольных значениях А, В и С последнее уравнение определя-
ет некоторую плоскость, принадлежащую связке плоскостей, проходящих
через точку
0
M . Его поэтому часто называют уравнением связки плоскостей.
Уравнение
l
++++
1111
DzCyBxA
(
)
0DzCyBxA
2222
=+++ (10)

17
при произвольном значении
l
определяет некоторую плоскость, проходя-
щую через прямую пересечения плоскостей
0DzCyBxA
1111
=+++ и 0DzCyBxA
2222
=+++ .
Уравнение плоскости, проходящей через три заданные точки
(
)
,z;y;xM
1111
(
)
2222
z;y;xM ,
(
)
3333
z;y;xM , имеет вид
.0
zzyyxx
zzyyxx
zzyyxx
131313
121212
111
=
---
---
---
(11)
24. Уравнение плоскости
021632
=
+
-
+
z
y
x
привести к нормально-
му виду.
∆ Находим нормирующий множитель (который берем со знаком “ми-
нус”, поскольку
021D
>
=
); .// 716321
222
-=++-=
m
Итак, нормальное
уравнение заданной плоскости имеет вид
.z)/(y)/(x)/( 03767972 =-+-- ▲
25. Определить расстояние от точки
0
M (3; 5; – 8) до плоскости
.
0
28
z
2
y
3
x
6
=
-
+
-
∆ Используя формулу (8) расстояния от точки до плоскости, находим
.
7
41
236
28)8(25336
d
222
=
++
--×+×-×
=
Так как результат подстановки координат точки
0
M в нормальное
уравнение плоскости отрицателен, то
0
M и начало координат лежат по одну
сторону от заданной плоскости. ▲
26. Составить уравнение плоскости, проходящей через точку М(2;3;5)
и перпендикулярной вектору
.k2j3i4N ++=
∆ Достаточно воспользоваться уравнением (9) плоскости, проходящей
через данную точку и перпендикулярной данному вектору:
,
0
)
5
z
(
2
)
3
y
(
3
)
2
x
(
4
=
-
+
-
+
-
т.е.
.
0
27
z
2
y
3
x
4
=
-
+
+
▲
27. Найти уравнение плоскости, проходящей через точку М(2; 3; -1)
параллельно плоскости
.
0
10
z
2
y
3
x
5
=
-
+
-
∆ Запишем уравнение (9) связки плоскостей, проходящих через дан-
ную точку: А(х-2)+В(у-3)+С(z+1) = 0.
Нормальный вектор искомой плоскости совпадает с нормальным век-
тором
)2;3;5(n -= данной плоскости. Следовательно, А = 5, В = -3, С = 2 и
уравнение искомой плоскости примет вид
,
0
)
1
z
(
2
)
3
y
(
3
)
2
x
(
5
=
+
+
-
-
-
или
.
0
1
z
2
y
3
x
5
=
+
+
-
▲

18
28. Из точки Р (2; 3; – 5) на координатные оси опущены перпендикуля-
ры. Составить уравнение плоскости, проходящей через их основания.
∆ Основаниями перпендикуляров, опущенных на координатные плоскости, слу-
жат следующие точки:
(
)
(
)
(
)
.5;3;0M,5;0;2M,0;3;2M
321
-- Используя соотно-
шение (11), запишем уравнение плоскости, проходящей через точки
321
M,M,M :
0
502
530
z3y2x
=
--
--
--
или
.
0
60
z
6
y
10
x
15
=
-
-
+
▲
29. Составить уравнение плоскости, проходящей через точку А (5; 4; 3)
и отсекающей равные отрезки на осях координат.
∆ Используя уравнение (4) плоскости в отрезках, в котором ,cba
=
=
имеем .1a/za/ya/x =++ Координаты точки А удовлетворяют уравнению ис-
комой плоскости, поэтому выполняется равенство ,1a/3a/4a/5 =++ откуда
12a
=
. Итак, получаем уравнение
.
0
12
z
y
x
=
-
+
+
▲
Прямая
Прямая может быть задана уравнениями двух плоскостей
,0DzCyBxA,0DzCyBxA
22221111
=+++=+++
пересекающихся по этой прямой.
Исключив поочередно х и у из предыдущих уравнений, получим урав-
нения .dbzy,cazx +=+= Здесь прямая определена двумя плоскостями,
проецирующими ее на плоскость
xOz
и
.
yOz
Уравнения прямой, проходящей через две точки )z;y;x(M
1111
и
),z;y;x(M
2222
имеют вид
.
zz
zz
yy
yy
xx
xx
12
1
12
1
12
1
-
-
=
-
-
=
-
-
(12)
Так называемые канонические уравнения
n
zz
m
yy
l
xx
111
-
=
-
=
-
определяют прямую, проходящую через точку )z;y;x(M
111
и параллельную
вектору .nkmjlis ++=
r
В частности, эти уравнения могут быть записаны в виде
,
cos
zz
cos
yy
cos
xx
111
gba
-
=
-
=
-
(13)
где
g
b
a
,
,
– углы, образованные прямой с осями координат. Направляющие
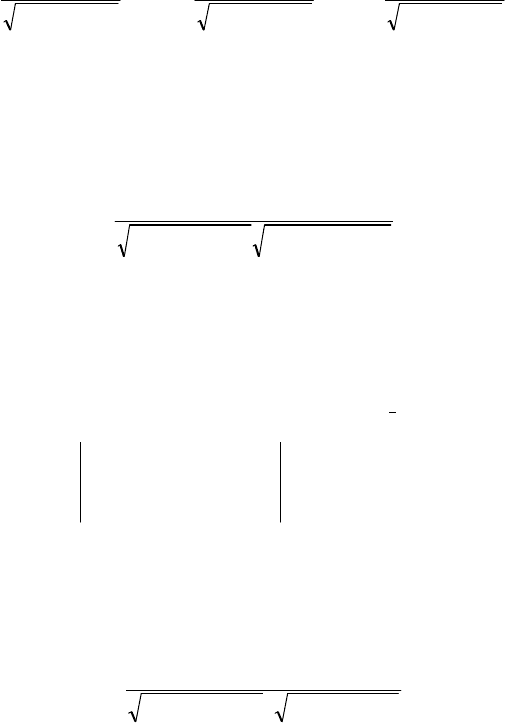
косинусы прямой находятся по формулам
19
.
nml
n
cos,
nml
m
cos,
nml
l
cos
222222222
++
=
++
=
++
=
gba
(14)
От канонических уравнений прямой, вводя параметр t, нетрудно пе-
рейти к параметрическим уравнениям:
.zntz,ymty,xltx
111
+=+=+= (15)
Угол между двумя прямыми, заданными их каноническими уравне-
ниями
111111
n/)zz(m/)yy(l/)xx( -=-=- и
222222
n/)zz(m/)yy(l/)xx( -=-=- , определяется по формуле
;
nmlnml
nnmmll
cos
2
2
2
2
2
2
2
1
2
1
2
1
212121
++++
+
+
j
(16)
условие параллельности двух прямых:
;n/nm/ml/l
212121
== (17)
условие перпендикулярности двух прямых:
0nnmmll
212121
=++ . (18)
Необходимое и достаточное условие нахождения двух прямых, задан-
ных их каноническими уравнениями, в одной плоскости (
условие компланар-
ности двух прямых):
0
nml
nml
zzyyxx
222
111
121212
=
---
. (19)
Если величины
111
n,m,l не пропорциональны величинам
222
n,m,l
, то
указанное соотношение является необходимым и достаточным условием пе-
ресечения двух прямых в пространстве.
Угол между прямой n/)zz(m/)yy(l/)xx(
111
-=-=- и плоско-
стью
0
D
Cz
y
B
Ax
=
+
+
+
определяется по формуле:
;
nmlCBA
CnBmAl
sin
222222
++×++
+
+
=
j
(20)
условие параллельности прямой и плоскости:
;0CnBmAl
=
+
+
(21)
условие перпендикулярности прямой и плоскости:
.n/Cm/Bl/A
=
=
(22)
Для определения точки пересечения прямой
n/)zz(m/)yy(l/)xx(
000
-=-=- с плоскостью
0
D
Cz
By
Ax
=
+
+
+
нужно решить совместно их уравнения, для чего следует воспользоваться
параметрическими уравнениями прямой
,xltx
0
+
=
,
0
y
mt
y
+=
:
0
z
nt
z
+
=
а) если
,
0
Cn
Bm
Al
¹
+
+
то прямая пересекает плоскость;

20
б) если
0CnBmAl =++
и ,0DCzByAx
000
¹+++ то прямая парал-
лельна плоскости;
в) если
0CnBmAl =++
и ,0DCzByAx
000
=+++ то прямая лежит в
плоскости.
30. Уравнения прямых
0
1
z
3
y
x
2
=
-
+
-
и
0
7
z
y
4
x
5
=
-
-
+
при-
вести к каноническому виду.
∆. Исключив сначала у, а затем z, имеем
011z11x13
=
-
+
и
.
0
22
y
11
x
17
=
-
+
Если разрешить каждое из уравнений относительно х, то получим
,
13
)1z(11
17
)2y(11
x
-
-
=
-
-
= т.е. .
13
1z
17
2y
11
x
-
=
-
=
-
▲
31. Составить уравнения прямой, проходящей через точку
)
1
;
2
;
3
(
M
-
и пересекающей ось
Ox
под прямым углом.
∆. Так как прямая перпендикулярна оси
Ox
и пересекает ее, то она
проходит через точку
).
0
;
0
;
3
(
N
Составив уравнения прямой, проходящей
через точки M и N, получаем
1
/
)
1
z
(
)
2
/(
)
2
y
(
0
/
)
3
x
(
+
=
-
-
=
-
. ▲
32. Дана плоскость
0
6
z
2
y
x
=
-
-
+
и вне ее точка
)
1
;
1
;
1
(
M
. Найти
точку N, симметричную точке M относительно данной плоскости.
∆. Запишем уравнения любой прямой, проходящей через точку М:
.n/)1z(m/)1y(l/)1x(
-
=
-
=
-
Координаты
{
}
n;m;l направляющего век-
тора прямой, перпендикулярной плоскости, можно заменить координатами
нормального вектора
{
}
2;1;1n -=
данной плоскости. Тогда уравнения этой
прямой запишутся в виде ).2/()1z(1/)1y(1/)1x( --=-=-
Найдем проекцию точки М на данную плоскость, решив совместно
уравнения
,
0
6
z
2
y
x
=
-
-
+
).
2
/(
)
1
z
(
1
/
)
1
y
(
1
/
)
1
x
(
-
-
=
-
=
-
Перепишем уравнения прямой в виде
.
1
t
2
z
,
1
t
y
,
1
t
x
+
-
=
+
=
+
=
Подставляя эти выражения для x, y и z в уравнение плоскости, найдем
,
1
t
=
откуда
.
1
z
,
2
y
,
2
x
-
=
=
=
Координаты симметричной точки найдутся из формул
(
)
,2/xxx
NM
+=
(
)
,2/yyy
NM
+=
(
)
,2/zzz
NM
+= т.е.
(
)
,2/x12
N
+=
(
)
,2/y12
N
+=
(
)
,2/z11
N
+=- откуда 3x
N
= ,
,3y
N
=
.3z
N
-= Следова-
тельно,
).
3
;
3
;
3
(
N
-
▲
33. Дана прямая
)
1
/(
)
1
z
(
3
/
y
2
/
)
1
x
(
-
+
=
=
-
и вне ее точка М(1; 1; 1).
Найти точку N, симметричную точке М относительно данной прямой.
∆. Уравнение плоскости, проецирующей точку М на данную прямую,
имеет вид
