Кумыкова С.К., Нахушева Ф.Б. Математика: Практикум по аналитической геометрии и алгебре

41

208. Найти объем треугольной пирамиды с вершинами А(0;0;1),

В(2;3;5), С(6;2;3) и D (3;7;2).

209. Построить пирамиду с вершинами О(0;0;0), А(5;2;0), В(2;5;0) и

С(1;2;4) и вычислить ее объем, площадь грани АВС и высоту пирамиды,

опущенную на эту грань.

210. Построить параллелепипед на векторах jia

r

43 += , kjb

r

+-= 3 ,

kjс

r

52 += и вычислить его объем. Правой или левой будет связка векторов

(

)

c,b,a

r

?

211. Показать, что векторы

kjia

r

v

r

23 ++-=

, kjib

r

432 --= ,

kjic

r

6123 ++-= компланарны, и разложить вектор

c

r

по векторам

a

r

и

b

r

.

212. Показать, что точки А(2; -1; -2), В(1; 2; 1), С(2; 3; 0) и D(5; 0; -6)

лежат в одной плоскости.

213. Показать, что: 1)

(

)

(

)

[

]

;cbabcaba

r

-=´´×+

2)

(

)

(

)

(

)

[

]

cbacbabacba

r

32 =--´-×-+ .

214. Построить пирамиду с вершинами А(2;0;0), В(0;3;0), С(0;0;6) и

D (2;3;8), вычислить ее объем и высоту, опущенную на грань АВС.

215. Построить векторы jib,kjia

r

24 -=++= и kjic

r

433 +-= ,

показать, что они компланарны, и разложить вектор

c

r

по векторам

a

r

и

b

r

.

216. Определить, какой является тройка сba

r

,, (правой или левой), если:

1) jc,ib,ka

r

=== ; 4) kc,jb,jia

r

==+= ;

2) jc,kb,ia

r

=== ; 5) jc,jib,jia

r

=-=+= ;

3)

kc,ib,ja

r

===

; 6) kc,jib,jia

r

=-=+= .

217. Векторы cba

r

,, , образующие правую тройку, взаимно перпенди-

кулярны. Зная, что 324 === c,b,a

r

, вычислить

cba

r

.

218-227. Даны векторы c,b,a

r

и d

r

в некотором базисе. Показать, что

вектора c,b,a

r

образуют базис и найти координаты вектора

d

r

в этом базисе:

218. ).;;(d),;;(c),;;(b),;;(a 14327584243371 ====

r

219. ).;;(d),;;(c),;;(b),;;(a 61814246274321 ====

r

220. ).;;(d),;;(c),;;(b),;;(a 17106537231321 =-=-==

r

221. ).;;(d),;;(c),;;(b),;;(a 13131142319874 --=-===

r

222. ).;;(d),;;(c),;;(b),;;(a 11471231064328 =-===

r

42

223. ).;;(d),;;(c),;;(b),;;(a 730192932441310 ====

r

224. ).;;(d),;;(c),;;(b),;;(a 62024135631142 ====

r

225. ).;;(d),;;(c),;;(b),;;(a 331821413586341 ====

r

226. ).;;(d),;;(c),;;(b),;;(a 16140234321115 ===--=

r

227. ).;;(d),;;(c),;;(b),;;(a 165132213321 ====

r

Определители, матрицы

228. Вычислить определитель:

321

125

432

-а) б)

15123

743

521

--

- в)

823

446

4612 -

г)

212

266

132

-

229. Найти х из уравнения

0

111

32

94

2

=х

х

230. Найти х из уравнения

0

410

11

23

2

=-х

х

231. Найти площадь треугольника с вершинами А(2;3), В(4;-1), С(6;5).

232. Найти сумму матриц А+В, если А=

÷

ø

ö

ç

è

æ

-

234

012

753

, В=

÷

ø

ö

ç

è

æ

-

--

101

232

421

233. Найти матрицу 2А+5В, если А= ,

÷

ø

ö

ç

è

æ

14

53

В=

÷

ø

ö

ç

è

æ

- 21

32

234. Найти произведение матриц

А=

÷

ø

ö

ç

è

æ

0

2

1

0

3

1

и В=

÷

ø

ö

ç

è

æ

-

102

415

101

43

235. Найти произведение матриц АВ и ВА, если

А=

÷

ø

ö

ç

è

æ

321

402

131

, В=

÷

ø

ö

ç

è

æ

-

123

211

012

236. Найти произведение матриц

А=

÷

ø

ö

ç

è

æ

-

--

113

112

234

и В=

÷

ø

ö

ç

è

æ

--

221

213

121

237. Найти произведение матриц

А=

÷

ø

ö

ç

è

æ

-100

110

321

и В=

÷

ø

ö

ç

è

æ

--

100

110

238. Найти матрицу, обратную к

А=

÷

ø

ö

ç

è

æ

-

211

112

111

239. Найти матрицу, обратную к

А=

÷

ø

ö

ç

è

æ

435

131

223

240. Найти А

3

, если А=

÷

ø

ö

ç

è

æ

41

23

241. Найти значение матричного многочлена 2А

2

+3А+5Е при

А=

÷

ø

ö

ç

è

æ

114

131

211

242. Вычислить АВ+3С, если

А=

÷

ø

ö

ç

è

æ

-

--

113

112

234

243. Найти значение А

2

+ВС, где

А=

÷

ø

ö

ç

è

æ

114

131

211

, В=

÷

ø

ö

ç

è

æ

-100

110

321

, С=

÷

ø

ö

ç

è

æ

--

100

110

44

244. Найти матрицу, обратную к

А=

÷

ø

ö

ç

è

æ

-

321

125

432

245. Найти матрицу, обратную к

А=

÷

ø

ö

ç

è

æ

--

-

15123

743

521

246. Найти матрицу, обратную к

А=

÷

ø

ö

ç

è

æ

-

823

446

4612

247. Найти матрицу, обратную к

А=

÷

ø

ö

ç

è

æ

-

212

266

132

248-257. Решить систему уравнений а) методом Крамера; б) средства-

ми матричного исчисления.

248.

ï

î

ï

í

ì

=++

=+-

.8x2xx

11xxx2

3xxx

321

249.

ï

î

ï

í

ì

=++

=-+

=++

.16xx4x3

14x3x2x

9x2x3x2

321

250.

ï

î

ï

í

ì

=++

.3z4y3x5

2zy3x

1z2y2x3

251.

ï

î

ï

í

ì

=-+

.3x3xx4

2x6x3x8

1xxx

321

252.

ï

î

ï

í

ì

=+-

=-+

=--

.11x4x2x3

11x2x4x3

4xxx2

321

253.

ï

î

ï

í

ì

=+-

-=++

=+-

.2zyx2

2z2y2x3

1zy2x

254.

ï

î

ï

í

ì

-=-+

=+-

.4z3yx4

5z4y5x

2zy3x2

255.

ï

î

ï

í

ì

-=++

-=+-

-=++

.2x4xx4

4x2xx2

1x2xx

321

256.

ï

î

ï

í

ì

=+-

.1z3y4x2

2z5yx3

3z4y2x

257.

ï

î

ï

í

ì

=++

.11x3xx2

1xx3x2

5xx2x3

321

45

АЛГЕБРА МАТРИЦ В ХИМИЧЕСКИХ ЗАДАЧАХ.

РАСЧЕТ НИТРУЮЩИХ СМЕСЕЙ

При расчетах нитрующих смесей обычно бывают заданными следую-

щие величины: общее количество смеси, которая должна быть приготовлена,

ее состав и состав всех исходных компонентов смеси; искомыми величинами

являются количества исходных компонентов, входящих в состав смеси.

В наиболее общем случае нитрующая смесь составляется из трех ком-

понентов, в состав которых входят азотная и серная кислоты и вода.

Примем следующие обозначения:

G – количество приготовляемой нитрующей смеси, кг;

I – содержание азотной кислоты в приготовляемой смеси, %;

т – содержание серной кислоты в приготовляемой смеси, %;

п – содержание воды в приготовляемой смеси, %;

G

а –

количество компонента а, идущего на приготовление смеси, кг;

а

l – содержание азотной кислоты в компоненте а, %;

m

а

– содержание серной кислоты в компоненте а, %;

n

а

– содержание воды в компоненте а, %;

G

b

– количество компонента b, идущего на приготовление смеси, кг;

b

l – содержание азотной кислоты в компоненте b, %;

m

b

– содержание серной кислоты в компоненте b, %;

n

b

, – содержание воды в компоненте b, %;

G

c

– количество компонента с, идущего на приготовление смеси, кг',

l

c

– содержание азотной кислоты в компоненте с, %;

m

c

– содержание серной кислоты в компоненте с, %;

n

c –

содержание воды в компоненте с, %.

Сумма количеств всех компонентов должна равняться количеству при-

готовленной смеси, т. е.

G

а

+G

b

+G

c

=G

Количество азотной кислоты, которое будет находиться в приготов-

ленной смеси:

ccbbaa

lGlGlGGl ×+×+×=

Количество серной кислоты в смеси:

ccbbaam

mGmGmGG ×+×+×=

Количество воды в смеси:

ccbbaan

nGnGnGG ×+×+×=

46

Решим совместно уравнения (2), (3), (4) и получим:

( )( )( )( )

bacacaba

cba

mmllmmll

mmm

llla -----==

111

Таким образом, имеем:

( )( )( )( )

кг

mmllmmll

G

mmllmmll

mmm

lllG

G

bacacaba

cbcbcc

bacacaba

cb

a

-----

=

-----

=

111

;

( )( )( )( )

кг

mmllmmll

G

mmllmmll

mmm

lllG

G

bacacaba

acacaa

bacacaba

ca

b

-----

=

-----

=

111

;

( )( )( )( )

кг

mmllmmll

G

mmllmmll

mmm

lllG

G

bacacaba

aababa

bacacaba

ba

c

-----

=

-----

=

111

.

Пример. Нитрующая смесь состава:

HNO

3

….

l

= 16%

H

2

SO

4

….m = 62%

H

2

O…. n = 22%

расходуется в количестве 4250 кг.

Эта смесь приготовляется из следующих растворов: меланж

HNO

3

- l

a

=85%, H

2

SO

4

-m

a

=10%, H

2

O-n

a

=5%

олеум (20%-ный) HNO

3

-l

b

=0; H

2

SO

4

-m

b

=104,5%; H

2

O-n

b

=0

отработанная кислота

HNO

3

- l

c

=0; H

2

SO

4

-m

c

=70%; H

2

O-n

c

=30%

Требуется определить расход кислот, идущих на приготовление нит-

рующей смеси данного состава.

Подставляя соответствующие значения в расчетные формулы, полу-

чим следующие расходы веществ.

Расход меланжа:

(

)

(

)

(

)

(

)

( )( )( )( )

кг

,

G

a

795

5104100857010085

6270085510470160

4250 =

-----

-

=

47

Расход олеума:

(

)

(

)

(

)

(

)

( )( )( )( )

кг

,

G

b

400

5104100857010085

62700857010160

4250 =

-----

-

=

Расход отработанной кислоты:

(

)

(

)

(

)

(

)

( )( )( )( )

кг

,

G

c

3055

5104100857010085

62108501051041685

4250 =

-----

-

=

Проверяя общее количество смеси, имеем

G=G

а

+G

b

+G

c

=795+400+3055=4250кг,

что соответствует заданному количеству нитрующей смеси.

Давление пара хлористого метилена

Для хлористого метилена, применяемого в качестве охлаждающего

средства, известны следующие три значения давления пара:

р

1

=0,0355 am при -30

0

С; (Т=243

0

К)

р

2

=0,190am при 0

0

С; (Т=273

0

К)

р

3

=1,020 am при 40

0

С; (Т=313

0

К)

Требуется найти давление пара хлористого метилена при –15

0

С и при

20

0

С. Используем следующую формулу:

CТlgB

Т

A

plg ++-= , (5)

где

2

21

2

11

ТТ

Т

lgB

p

lgA

a

-

÷

ø

ö

ç

è

æ

-=

,

9871,

cc

B

pFpD

-

=

причем с

рD

и с

рD

-средние мольные теплоемкости вещества, соответственно,

в парообразном и жидком состоянии при постоянном давлении

11

ТlgB

Т

A

plgС -+=

Т – температура,

0

К

Подставляя в (5) известные значения для Р и Т, получим три уравнения

с тремя неизвестными А, В и С.

Имеем:

( )

11

1

plgCBТlgA

Т

=++- ,

( )

22

2

1

plgCBТlgA

Т

=++- ,

( )

33

3

1

plgCBТlgA

Т

=++- .

48

Кроме того

4

1

1015241

1

-

××-=-

Т

; 385612

1

,Тlg = ; 449771

1

,plg -=

4

2

1063036

1

-

×-=- ,

Т

; 436162

2

,Тlg = ; 721250

2

,plg -=

4

3

1094931

1

-

×=- ,

T

; 495542

3

,Tlg = ; 008600

3

,plg -= .

Отсюда получаем:

1

3

2

1

33

22

11

Tlg

T

Tlg

T

Tlg

T

Tlgplg

A

-

= ;

1

3

2

1

3

2

1

Tlg

T

Tlg

T

Tlg

T

plg

T

plg

T

plg

T

B

-

=

или

(

)

(

)

(

)

(

)

( ) ( )

12

21

13

21

12131312

1111

TlgTlg

TT

TlgTlg

TT

TlgTlgplgplgTlgTlgplgplg

A

-

÷

ø

ö

ç

è

æ

---

÷

ø

ö

ç

è

æ

-

= ;

( ) ( )

12

31

13

21

12

21

13

21

1111

TlgTlg

TT

TlgTlg

TT

plgplg

TT

plgplg

TT

B

-

÷

ø

ö

ç

è

æ

---

÷

ø

ö

ç

è

æ

-

÷

ø

ö

ç

è

æ

---

÷

ø

ö

ç

è

æ

-

= .

Величина С определяется при подстановке найденных значений А и В

в одно из начальных уравнений. В итоге получаем:

61995

050550102039109930105224

050550458371109930728520

44

,

,,,,

А =

××-××

×

-

×

=

--

;

В=-3,4426;

9754143867830997721250

2

,,,,TlgB

T

A

plgС =++-=-+= .

49

Таким образом

97541444263

61995

,Tlg,

T

,

plg +--=

С помощью этой формулы окончательно найдем

р=0,470 am при 20

0

С (Т=293

0

К)

и р=0,0867 am при -15

0

С (Т=258

0

К)

Кинетика последовательно-параллельных

химических реакций первого порядка

Рассмотрим смесь, состоящую из m веществ с концентрациями А

1

,

А

2

,…., А

m

, и предположим, что каждое из них может вступать во взаимодей-

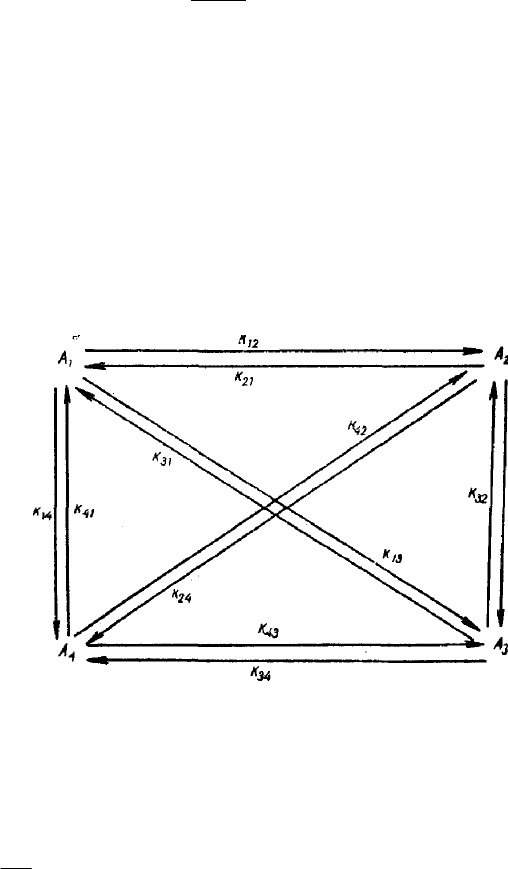
ствие соответственно реакции первого порядка. Например, при m=4 схема

взаимодействия вещества будет следующей (аналогичную схему можно со-

ставить для любого значения m):

Пусть константы скоростей реакций будут k

ij

, причем первый индекс

относится к веществу, вступающему в реакцию, а второй – к образующемуся

продукту. Примем, что стехиометрические уравнения выражают соотноше-

ния, при которых из одного моля исходного вещества образуется один моль

продукта. Тогда система из т стехиометрических уравнений кинетики при-

обретает следующий вид:

mmiiiii

Ak...AkAk...AkAk

d

dA

+++++--=

22111211

1

t

(i=1,…, m)

или

50

( )

mmiiiimii

i

Ak...AkAkAk...kk

d

dA

++++----=

221121

t

(i=1,…, m). (1)

Эта система из m обыкновенных дифференциальных уравнений с m

зависимыми переменными решается в конечном виде.

Перепишем (1) следующим образом:

å

=

=+

m

i

jij

i

Ak

d

dA

1

0

t

, (2)

где К

ij

=-k

ij

при j¹1 и K

ii

=

å

¹

=

m

ip

p

ip

k

1

.

Будем искать частное решение в виде

lt

-

= eBA

ii

, (3)

где постоянные

i

B и

l

отыскиваются из условия удовлетворения началь-

ным условиям задачи и уравнению (2). Подстановка (3) в (2) с после-

дующим исключением экспоненты дает систему однородных линей-

ных уравнений относительно величины В

i

:

å

=

=+-

m

i

jiji

BkB

1

0

l

( i =1,…, m ) (4)

или

( )

å

=

=-

m

j

iijij

Bk

1

0

ld

( i =1,2,…, m ), (5)

где

î

í

ì

=

¹

=

ji

ij

1

0

d

Однородная система (5) имеет ненулевые решения В

i

только в том

случае, если определитель, составленный из коэффициентов, равен нулю, т.е.

0=-

ld

ijij

k (6)

В развернутом виде это алгебраическое уравнение m-й степени отно-

сительно

l

, которое должно иметь, вообще говоря, m различных корней.

Обозначим эти значения

l

через

r

l

, где r=1,2,…,m. Для каждого

r

l

мы

будем иметь группу значений В

j

, которые являются решениями (5) и опреде-

лены с точностью до произвольного множителя. Обозначим их через В

jr

.

Как правило, с помощью одного только решения оказывается невоз-

можным удовлетворить начальным условиям концентрации. Поэтому необ-

Кумыкова С.К., Нахушева Ф.Б. Математика: Практикум по аналитической геометрии и алгебре

Подождите немного. Документ загружается.