Лаврусь О.Е. (сост.), Лаврусь В.В. (сост.) Методические указания и варианты заданий к экзаменационному тесту (ряды, теория вероятностей, математическая статистика) для студентов заочной формы обучения

Подождите немного. Документ загружается.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика) Составитель: Лаврусь О.Е.

Лаврусь В.В.

ВАРИАНТ 20

1. Знаменатель геометрической прогрессии 1; 0,1; 0,01… равен:

A) 0,1;

B) 10;

C) 0,9;

D) 0,01.

2. Первые три члена ряда

()

−

∞

−⋅

∑

имеют вид:

−+−

;

+−

;

−−

;

−−−

3. Общий член ряда

+−−

… равен:

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

4. Сумма первых трех членов ряда

()

∑

∞

⋅−

равна:

; B) –

; C) –

5. Найти интервал сходимости функционального ряда

()

∑

∞

A) – 2 < x < 2;

B) – 4 < x < 4;

C) 2 < x < 6;

D) – 6 < x < – 2.

6.. Вероятность Р(А) появления хотя бы одного из событий А

и А

с вероятностями

Р(А

) и Р(А

) находится по формуле:

A) Р(А) =

() ()

1 APAP ⋅−

;

B) Р(А) = Р(А

)·Р(А

);

C) Р(А) =

() ()

APAP ⋅

;

D) Р(А) =

() ()

1 APAP ⋅−

7. Комбинации, число которых определяется по формуле

()

mnm

−

, называются:

A) размещениями;

B) сочетаниями;

C) перестановками;

D) размещениями с повторением.

8. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном

выстреле для первого стрелка равна 0,5, для второго – 0,4. Найти вероятность того, что

хотя бы один стрелок попадет в мишень.

A) 0,9;

B) 0,2;

C) 0,6;

D) 0,7.

9. Монету бросают 5 раз. Найти вероятность того, что «герб» выпадет ровно 1 раз.

A) 5/16;

B) 3/5;

C) 5/32;

D) 3/16.

10. Вероятность наступления события A в каждом испытании равна 0,6. Вероятность

того, что в результате проведения 100 независимых испытаний событие A наступит

более 30 раз, вычисляется:

A) по формуле Пуассона;

B) по интегральной формуле Лапласа;

C) по формуле Бернулли;

D) по локальной формуле Муавра-Лапласа.

11. Дисперсия случайной величины X обладает следующим свойством

A) 0 ≤ D(X) ≤ 1;

B) D(X) ≥ 0;

C) D(X) ≠ 0;

D) D(X) ≥ 1.

12. Дискретная случайная величина X задана законом распределения:

– 1 0 5

0,2 0,4

Математическое ожидание M(X) этой случайной величины равно:

A) 2;

B) 3;

C) 1,8;

D) 1,6.

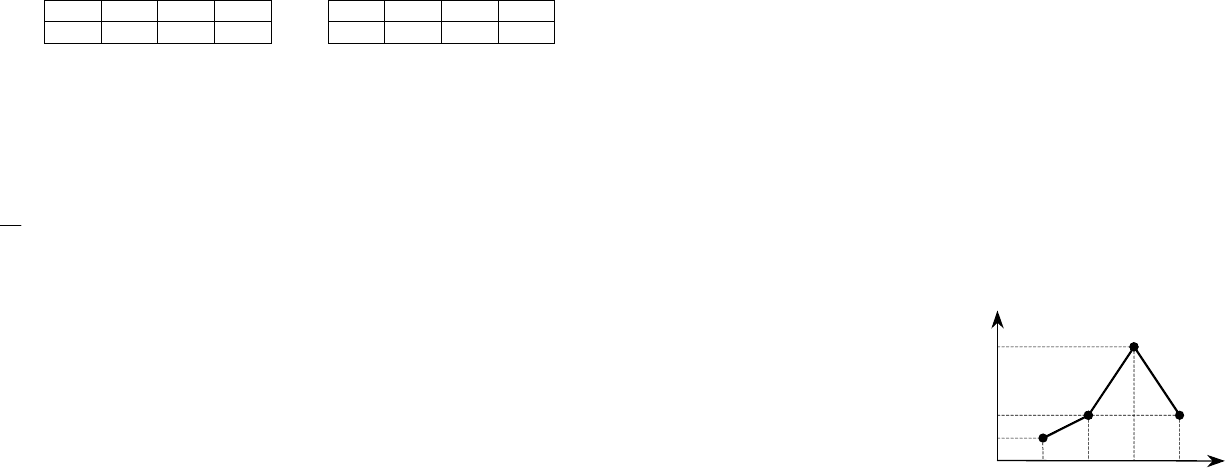
ВАРИАНТ 20

13. Найти математическое ожидание случайной величины Z = X·Y, если известны

законы распределения независимых случайных величин X и Y:

0 2 5

0 4 6

0,1 0,5 0,4

0,4 0,3 0,3

A) 6;

B) 9;

C) 8;

D) 7.

14. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.6при1

;60при

0;при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (2, 4).

A) 1/9;

B) 1/3;

C) 2/3;

D) 5/9.

15. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.1при0

;10при2

;0при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (0,5; 1).

A) 0,75;

B) 0,25;

C) 0,48;

D) 0,12.

16. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.1при0

;10при

;0при0

Коэффициент γ равен:

A) 2;

B) 3;

C) 4;

D) 5.

17. Найти моду статистической выборки: 1, 4, 3, 2, 5, 5, 4, 2, 4, 3, 1.

A) 5;

B) 4;

C) 3;

D) 2.

18. Если основная гипотеза имеет вид H

: a = 8, то конкурирующей может быть

гипотеза:

A) Н

: a ≠ 7;

B) Н

: a ≥ 8;

C) Н

: a ≤ 8;

D) Н

: a < 8.

19. Точечная оценка математического ожидания случайной величины, распределенной

по нормальному закону, равна 16,5. Тогда его интервальная оценка может быть

записана в виде:

A) (16; 18);

B) (16; 17);

C) (15; 17);

D) (15,5; 17).

20. Из генеральной совокупности извлечена выборка объема n = 80, полигон

относительных частот которой имеет вид

468

Тогда число вариант x

= 8 в выборке равно:

A) 32;

B) 16;

C) 8;

D) 14;

21. Выборочное уравнение парной регрессии имеет вид y = 2x – 4. Тогда выборочный

коэффициент корреляции может быть равен:

A) 0;

B) – 2;

C) – 0,8;

D) 0,8.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика) Составитель: Лаврусь О.Е.

Лаврусь В.В.

ВАРИАНТ 21

1. Если знакоположительный числовой ряд

∑

∞

a сравнить с рядом

∑

∞

b , который

расходится, то при a

> b

можно утверждать, что ряд

∑

∞

a :

A) сходится;

B) расходится;

C) требует дополнительных исследований;

D) отвечает второму признаку сходимости.

2. Сумма чисел от 1 до 100 включительно равна:

A) 505;

B) 5000;

C) 5100;

D) 5050.

3. Общий член ряда

−+−

+ … равен:

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

;

()

∑

∞

⋅−

4. Сумма первых трех членов ряда

()

∑

∞

−

⋅−

равна:

; B) –

; C) –

; D)

5. Найти интервал сходимости функционального ряда

()

∑

∞

−

A) – 2 < x < 2;

B) – 4 < x < 4;

C) 2 < x < 6;

D) – 6 < x < – 2.

6. События, образующие полную группу, не могут быть:

A) несовместными;

B) равновозможными;

C) совместными;

D) противоположными.

7. Формула полной вероятности имеет вид:

() ( ) ( )

∑

⋅=

AHPHPAP

() () ( )

∑

∞

⋅=

AHPAPHP ;

() ( ) ( )

∑

⋅=

HAPHPAP

() ( ) ( )

∑

∞

⋅=

AHPHPAP .

8. Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй – 0,8; третий –

0,7. Найти вероятность того, что студент сдаст только первый экзамен.

A) 0,333;

B) 0,054;

C) 0,024;

D) 0,994.

9. Стрелок производит 3 выстрела по мишени. Вероятность попадания в мишень при

каждом выстреле одинакова и равна 0,8. Найти вероятность того, что стрелок попадет в

мишень не более одного раза.

A) 0,8;

B) 0,104;

C) 0,384;

D) 0,096.

10. Вероятность наступления события A в каждом испытании равна 0,5. Вероятность

того, что в результате проведения 400 независимых испытаний событие A наступит

ровно 200 раз, вычисляется:

A) по локальной формуле Муавра-Лапласа;

B) по интегральной формуле Лапласа;

C) по формуле Бернулли;

D) по формуле Пуассона.

11. Функция плотности случайной величины X обладает следующим свойством

A) f(x) > 1;

B) f(x) ≥ 0;

C) 0 ≤ f(x) ≤ 1;

D) – ∞ < f(x) < + ∞.

12. Дискретная случайная величина X принимает значения 3, 4, – 2, – 7, 8 с равными

вероятностями. Математическое ожидание M(X) этой случайной величины равно:

A) 1,2;

B) 1,4;

C) 1,6;

D) 2.

ВАРИАНТ 21

13. Найти математическое ожидание случайной величины Z = X + Y, если известны

законы распределения независимых случайных величин X и Y:

3 6 0

5 8 0

0,4 0,5 0,1

0,2 0,5 0,3

A) 20;

B) 18;

C) 21;

D) 9,2.

14. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<−

−≤

.2при1

;21при

;1при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (1, 2).

A) 2/9;

B) 1/9;

C) 5/9;

D) 7/9.

15. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.1при0

;10при4

;0при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (0,5; 1).

A) 1/5;

B) 1/4;

C) 1/2;

D) 3/4.

16. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.при1

;0при

0;при0

Коэффициент β равен:

A) 2;

B) 3;

C) 4;

D) 5.

17. Найти моду статистической выборки: 5, 1, 7, 7, 1, 5, 3, 3, 1, 4.

A) 7;

B) 5;

C) 3;

D) 1.

18. Если основная гипотеза имеет вид H

: a =4 , то конкурирующей может быть

гипотеза:

A) Н

: a ≥ 4;

B) Н

: a > 4;

C) Н

: a ≤ 4;

D) Н

: a ≠ 5.

19. Точечная оценка математического ожидания случайной величины, распределенной

по нормальному закону, равна 4,5. Тогда его интервальная оценка может быть записана

в виде:

A) (3,7; 5);

B) (3,6; 4,4);

C) (3; 5);

D) (4; 6).

20. Из генеральной совокупности извлечена выборка объема n = 30, полигон

относительных частот которой имеет вид

6912

Тогда число вариант x

= 12 в выборке равно:

A) 9;

B) 6;

C) 12;

D) 9;

21. Выборочное уравнение парной регрессии имеет вид y = – 3 + 2x. Тогда выборочный

коэффициент корреляции может быть равен:

A) – 3;

B) 2;

C) – 0,67;

D) 0,8.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика) Составитель: Лаврусь О.Е.

Лаврусь В.В.

ВАРИАНТ 22

1. Для знакоположительного числового ряда

∑

∞

a p

→∞

lim называется:

A) радикальным признаком Коши;

B) признаком сравнения;

C) признаком Лейбница;

D) признаком Даламбера.

2. Первые три члена ряда

()

−⋅

∑

∞

имеют вид:

−+− ;

+−

;

−−

3. Общий член ряда

+−−

… равен:

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

4. Сумма первых трех членов ряда

()

∑

∞

−

⋅−

равна:

; B) –

; C)

; D)

5. Найти интервал сходимости функционального ряда

()

∑

∞

A) – 3 < x < 3;

B) – 8 < x < – 2;

C) – 5 < x < 5;

2 < x < 8.

6. Вероятность события A равна P(A) = 0,4. Вероятность P( А ) противоположного

события А равна:

A) P(

) = 0,5;

B) P(

) = 0,6;

C) P(

) = 1;

D) P(

) = 0.

7. Формула

()

−

⋅

называется формулой:

A) Лапласа;

B) полной вероятности;

C) Бернулли;

D) Пуассона.

8. В урне содержится 5 одинаковых шаров, причем 3 из них белого цвета, а 2 – красного.

Наудачу извлечены 3 шара. Найти вероятность того, что среди трех извлеченных шаров

окажется один красный шар.

A) 0,6;

B) 0,4;

C) 0,3;

D) 0,5.

9. Монету бросают 3 раза. Найти вероятность того, что «герб» выпадет ровно 2 раза.

A) 0,5;

B) 0,125;

C) 0,375;

D) 0,25.

10. Вероятность наступления события A в каждом испытании равна 0,6. Вероятность

того, что в результате проведения 2000 независимых испытаний событие A наступит

менее 1400 раз, вычисляется:

A) по формуле Бернулли;

B) по интегральной формуле Лапласа;

C) по локальной формуле Муавра-Лапласа;

D) по формуле Пуассона.

11. Вероятность того, что непрерывная случайная величина X примет значение,

принадлежащее интервалу (a, b) определяется по формуле:

()()

∫

=<<

dxxFbXaP

; B)

()()

∫

⋅=<<

dxxfxbXaP

;

()()

∫

=<<

dxxfbXaP

; D)

()()

∫

⋅=<<

dxxFxbXaP

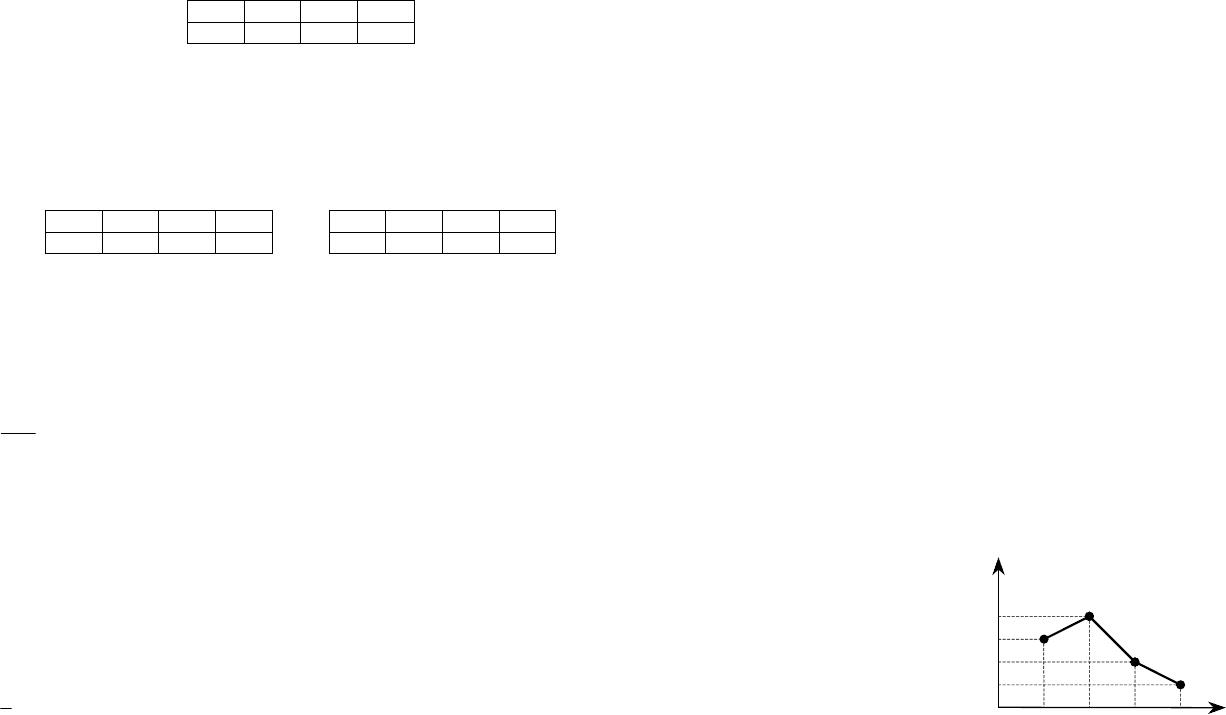
ВАРИАНТ 22

12. Дискретная случайная величина X задана законом распределения:

– 3 0 1

0,2 0,4 p

Дисперсия D(X) этой случайной величины равна:

A) 1;

B) 2,2;

C) – 0,2;

D) 2,6.

13. Найти математическое ожидание случайной величины Z = 2X + Y, если известны

законы распределения независимых случайных величин X и Y:

0 2 5

0 4 6

0,1 0,5 0,4

0,4 0,3 0,3

A) 9;

B) 6;

C) 8;

D) 7.

14. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<−

−≤

.2при1

;21при

;1при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (0, 3).

A) 1/3;

B) 2/3;

C) 1;

D) 0,5.

15. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<−

−≤

.2при0

;21при

;1при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (1, 2).

A) 2/3;

B) 3/4;

C) 1/3;

D) 1/2.

16. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.1при0

;10при

;0при0

Коэффициент γ равен:

A) 1;

B) 2;

C) 3;

D) 4.

17. Найти моду статистической выборки: 2, 4, 3 2, 5, 3, 4, 2, 5, 1.

A) 2;

B) 5;

C) 4;

D) 3.

18. Если основная гипотеза имеет вид H

: a = 18, то конкурирующей может быть

гипотеза:

A) Н

: a ≠ 17;

B) Н

: a ≥ 18;

C) Н

: a < 18;

D) Н

: a ≤ 18.

19. Точечная оценка математического ожидания случайной величины, распределенной

по нормальному закону, равна 17,5. Тогда его интервальная оценка может быть

записана в виде:

A) (17; 19);

B) (16; 18);

C) (16; 19);

D) (16,5; 19).

20. Из генеральной совокупности извлечена выборка объема n = 40, полигон

относительных частот которой имеет вид

81216

Тогда число вариант x

= 16 в выборке равно:

A) 12

B) 10

C) 16

D) 4

21. Выборочное уравнение парной регрессии имеет вид y = 3x + 4. Тогда выборочный

коэффициент корреляции может быть равен:

A) 3;

B) 0;

C) 0,7;

D) – 0,7.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика) Составитель: Лаврусь О.Е.

Лаврусь В.В.

ВАРИАНТ 23

1. Дан знакоположительный числовой ряд

∑

∞

a . Тогда

∞→

lim

называется

достаточным признаком:

A) радикальным Коши;

B) сравнения;

C) Маклорена;

D) Даламбера.

2. Первые три члена ряда

()

−⋅

∑

∞

имеют вид:

;

+−

;

+−−

;

−+−

3. Общий член ряда

+−

… равен:

()

∑

∞

⋅−

;

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

;

()

∑

∞

⋅−

4. Сумма первых трех членов ряда

()

∑

∞

−

⋅−

равна:

; B) – 3; C) 2; D) – 2.

5. Найти интервал сходимости функционального ряда

()

∑

∞

−

A) – 3 < x < 3;

B) – 8 < x < – 2;

C) – 5 < x < 5;

2 < x < 8.

6. Вероятности событий А, В, С, образующих полную группу, равны:

A) Р(А) = 1/4, Р(В) = 1/6, Р(С) = 3/4;

B) Р(А) = 1/5, Р(В) = 3/10, Р(С) = 1/2;

C) Р(А) = 1/3, Р(В) = 1/6, Р(С) = 5/6;

D) Р(А) = 1/7, Р(В) = 2/7, Р(С) = 3/7.

7. Если вероятность р наступления события А в каждом испытании постоянна и

отлична от нуля и единицы, то при достаточно большом числе n независимых

испытаний вероятность того, что частость m/n события А отличается от его

вероятности р не более, чем на величину Δ > 0 (по абсолютной величине) равна:

⎟

⎠

⎞

⎜

⎝

⎛

Δ≈

⎟

⎠

⎞

⎜

⎝

⎛

Δ≤−

Фp

⎟

⎠

⎞

⎜

⎝

⎛

Δ≈

⎟

⎠

⎞

⎜

⎝

⎛

Δ≤−

Фp

⎟

⎠

⎞

⎜

⎝

⎛

≈

⎟

⎠

⎞

⎜

⎝

⎛

Δ≤−

npq

Фp

()

npqФp

Δ≈

⎟

⎠

⎞

⎜

⎝

⎛

Δ≤− 2.

8. Среди 10 лотерейных билетов 2 выигрышных. Наудачу выбирают 2 билета. Найти

вероятность того, что оба билета окажутся выигрышными.

A) 1/45;

B) 28/45;

C) 1/5;

D) 16/45.

9. В семье 5 детей. Считая вероятность рождения мальчика и девочки равными между

собой, найти вероятность того, что в данной семье одна девочка.

A) 3/16;

B) 5/32;

C) 1/5;

D) 4/5.

10. Вероятность поражения мишени при одном выстреле равна 0,8. Вероятность того,

что в результате 100 выстрелов мишень будет поражена менее 75 раз, вычисляется:

A) по формуле Бернулли;

B) по интегральной формуле Лапласа;

C) по локальной формуле Муавра-Лапласа;

D) по формуле Пуассона.

11. Функция распределения F(x) = P(X < x), выражающая для каждого значения x

вероятность того, что случайная величина X примет значение, меньшее x, является:

A) убывающей;

B) периодической;

C) возрастающей;

D) четной.

ВАРИАНТ 23

12. Дискретная случайная величина X задана законом распределения:

3 4

0,3 0,4 0,3

Если известно, что ее математическое ожидание M(X) равно 2,1, то x

равно:

A) 0;

B) 1;

C) – 1;

D) 2.

13. Найти дисперсию случайной величины Z = 5 – 3X, если известна дисперсия

случайной величины X: D(X) = 3.

A) 27;

B) 32;

C) – 22;

D) 14.

14. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.5при1

;50при

0;при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (2, 4).

A) 16/25;

B) 3/25;

C) 8/25;

D) 12/25.

15. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.3при0

;30при

;0при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (1, 3).

A) 5/9;

B) 8/9;

C) 1/9;

D) 1/3.

16. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<+

≤

.0при1

;0при

;при0

Коэффициент α равен:

A) –8;

B) – 1;

C) – 5;

D) – 2.

17. Найти моду статистической выборки

1, 2, 6, 7, 7, 3, 2, 3, 6, 2, 5.

A) 7;

B) 6;

C) 3;

D) 2.

18. Если основная гипотеза имеет вид H

: a =15 , то конкурирующей может быть

гипотеза:

A) Н

: a ≠ 14;

B) Н

: a ≤ 15;

C) Н

: a ≥ 15;

D) Н

: a > 15.

19. Точечная оценка математического ожидания случайной величины, распределенной

по нормальному закону, равна 18,5. Тогда его интервальная оценка может быть

записана в виде:

A) (17,2; 19,8);

B) (17; 19);

C) (18; 20);

D) (16,4; 20,4).

20. Из генеральной совокупности извлечена выборка объема n = 60, полигон

относительных частот которой имеет вид

10 15 20

Тогда число вариант x

= 15 в выборке равно:

A) 15;

B) 12;

C) 6;

D) 4.

21. Выборочное уравнение парной регрессии имеет вид y = – 2 + 3x. Тогда выборочный

коэффициент корреляции может быть равен:

A) – 2;

B) 3;

C) 0,6;

D) – 0,8.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика) Составитель: Лаврусь О.Е.

Лаврусь В.В.

ВАРИАНТ 24

1. Рассматривается сходимость знакоположительного числового ряда по формуле

→∞

lim . Тогда справедливо утверждение, что ряд сходится при

A) p = 1;

B) p < 1;

C) p > 1;

D) p = 2.

2. Третий член ряда

()

−

∞

−⋅

∑

равен:

A) 1/8;

B) – 1/9;

C) – 1/4;

D) 1/9.

3. Общий член ряда

−++−

… равен:

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

4. Сумма первых трех членов ряда

∑

∞

−

равна:

; B) –

; C) –

; D)

5. Найти интервал сходимости функционального ряда

()

∑

∞

−

A) – 2 < x < 2;

B) – 6 < x < 6;

C) 4 < x < 8;

D) – 8 < x < 4.

6. Вероятности событий А, В, С, образующих полную группу, равны:

A) Р(А) = 1/6, Р(В) = 1/3, Р(С) = 1/4;

B) Р(А) = 1/3, Р(В) = 1/3, Р(С) = 1/2;

C) Р(А) = 1/7, Р(В) = 3/7, Р(С) = 3/7;

D) Р(А) = 1/2, Р(В) = 1/3, Р(С) = 2/3.

7. Формула

() ( ) ( )

∑

⋅=

HAPHPAP

/ называется формулой:

A) Бернулли;

B) полной вероятности;

C) Пуассона;

D) Байеса.

8. В урне содержится 5 одинаковых шаров, причем 3 из них окрашены. Наудачу

извлечены 2 шара. Найти вероятность того, что среди двух извлеченных шаров

окажется хотя бы один окрашенный шар.

A) 0,5;

B) 0,8;

C) 0,6;

D) 0,9.

9. Вратарь отражает пенальти с вероятностью 0,5. Найти вероятность того, что вратарь

отразит 2 пенальти из 5.

A) 2/5;

B) 2/32;

C) 5/32;

D) 5/16.

10. Вероятность наступления события A в каждом испытании равна 0,9. Вероятность

того, что в результате проведения 100 независимых испытаний событие A наступит

ровно 80 раз, вычисляется:

A) по формуле Бернулли;

B) по интегральной формуле Лапласа;

C) по локальной формуле Муавра-Лапласа;

D) по формуле Пуассона.

11. Наиболее вероятное значение случайной величины X называют:

A) медианой;

B) квантилем;

C) центральным моментом;

D) модой.

12. Дискретная случайная величина X задана законом распределения:

– 2 0 4

0,3 0,4

Математическое ожидание M(X) этой случайной величины равно:

A) 2,2;

B) 1,5;

C) 1,3;

D) 1.

ВАРИАНТ 24

13. Найти математическое ожидание случайной величины Z = X·Y, если известны

законы распределения независимых случайных величин X и Y:

034

024

0,3 0,2 0,5

0,1 0,4 0,5

A) 2,8;

B) 2,6;

C) 6,28;

D) 7,28.

14. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.3при1

;30при

0;при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (2, 3).

A) 4/9;

B) 5/9;

C) 1/3;

D) 2/9.

15. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.3при0

;30при

;0при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (2, 3).

A) 19/27;

B) 1/9;

C) 7/27;

D) 1/27.

16. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.при0

;0при5,0

;0при0

Коэффициент β равен:

A) 1;

B) 4;

C) 3;

D) 2.

17. Найти моду статистической выборки: 2, 1, 5, 4, 1, 3, 2, 1, 5, 3.

A) 5;

B) 4;

C) 1;

D) 3.

18. Если основная гипотеза имеет вид H

: a = 13, то конкурирующей может быть

гипотеза:

A) Н

: a < 13;

B) Н

: a ≤ 13;

C) Н

: a ≥ 13;

D) Н

: a ≠ 12.

19. Точечная оценка математического ожидания случайной величины, распределенной

по нормальному закону, равна 20,5. Тогда его интервальная оценка может быть

записана в виде:

A) (20; 22);

B) (20; 21,5);

C) (20,5; 21);

D) (19,5; 21,5).

20. Из генеральной совокупности извлечена выборка объема n = 100, полигон

относительных частот которой имеет вид

12 18 24

Тогда число вариант x

= 24 в выборке равно:

A) 24;

B) 50;

C) 30;

D) 40;

21. Выборочное уравнение парной регрессии имеет вид y = – 1,5x + 2. Тогда выборочный

коэффициент корреляции может быть равен:

A) – 1,5;

B) – 0,7;

C) 2;

D) 0,67.