Лаврусь О.Е. (сост.), Лаврусь В.В. (сост.) Методические указания и варианты заданий к экзаменационному тесту (ряды, теория вероятностей, математическая статистика) для студентов заочной формы обучения

Подождите немного. Документ загружается.

Экзаменационные тесты (ряды, теория вероятностей, математическая статистика) Составитель: Лаврусь О.Е.

Лаврусь В.В.

ВАРИАНТ 30

1. Если знакоположительный числовой ряд

∑

∞

a сравнить с рядом

∑

∞

b , который

расходится, то при a

> b

можно утверждать, что ряд

∑

∞

a :

A) сходится;

B) требует дополнительных исследований;

C) расходится;

D) отвечает второму признаку сходимости.

2. Третий член ряда

∑

∞

равен:

A) 3/5;

B) 1/2;

C) 3/7;

D) 1.

3. Общий член ряда

−++−

… равен:

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

;

()

∑

∞

−

⋅−

4. Сумма первых трех членов ряда

()( )

∑

∞

−⋅−

равна:

A) –

; B)

; C) –

; D)

5. Найти интервал сходимости функционального ряда

()

∑

∞

−

A) 3 < x < 11;

B) – 4 < x < 4;

C) – 7 < x < 7;

D) – 11 < x < 3.

6. События, образующие полную группу, не могут быть:

A) несовместными;

B) совместными;

C) противоположными;

D) равновозможными.

7. Число сочетаний из n элементов по m находится по формуле:

()

mnm

−

= ;

()

mnn

−

= ;

()

mnm

= ;

()

nmm

−

= .

8. Вероятность того, что студент сдаст первый экзамен, равна 0,9; второй – 0,8; третий –

0,7. Найти вероятность того, что студент сдаст хотя бы один экзамен.

A) 0,5;

B) 0,333;

C) 0,994;

D) 0,998.

9. Монету бросают 3 раза. Найти вероятность того, что «герб» выпадет менее двух раз.

A) 0,375;

B) 0,125;

C) 0,25;

D) 0,5.

10. Вероятность наступления события A в каждом испытании равна 0,004. Вероятность

того, что в результате проведения 1000 независимых испытаний событие A наступит

ровно 6 раз, вычисляется:

A) по формуле Пуассона;

B) по интегральной формуле Лапласа;

C) по формуле Бернулли;

D) по локальной формуле Муавра-Лапласа.

11. Наиболее вероятное значение случайной величины X называют:

A) медианой;

B) модой;

C) центральным моментом;

D) квантилем.

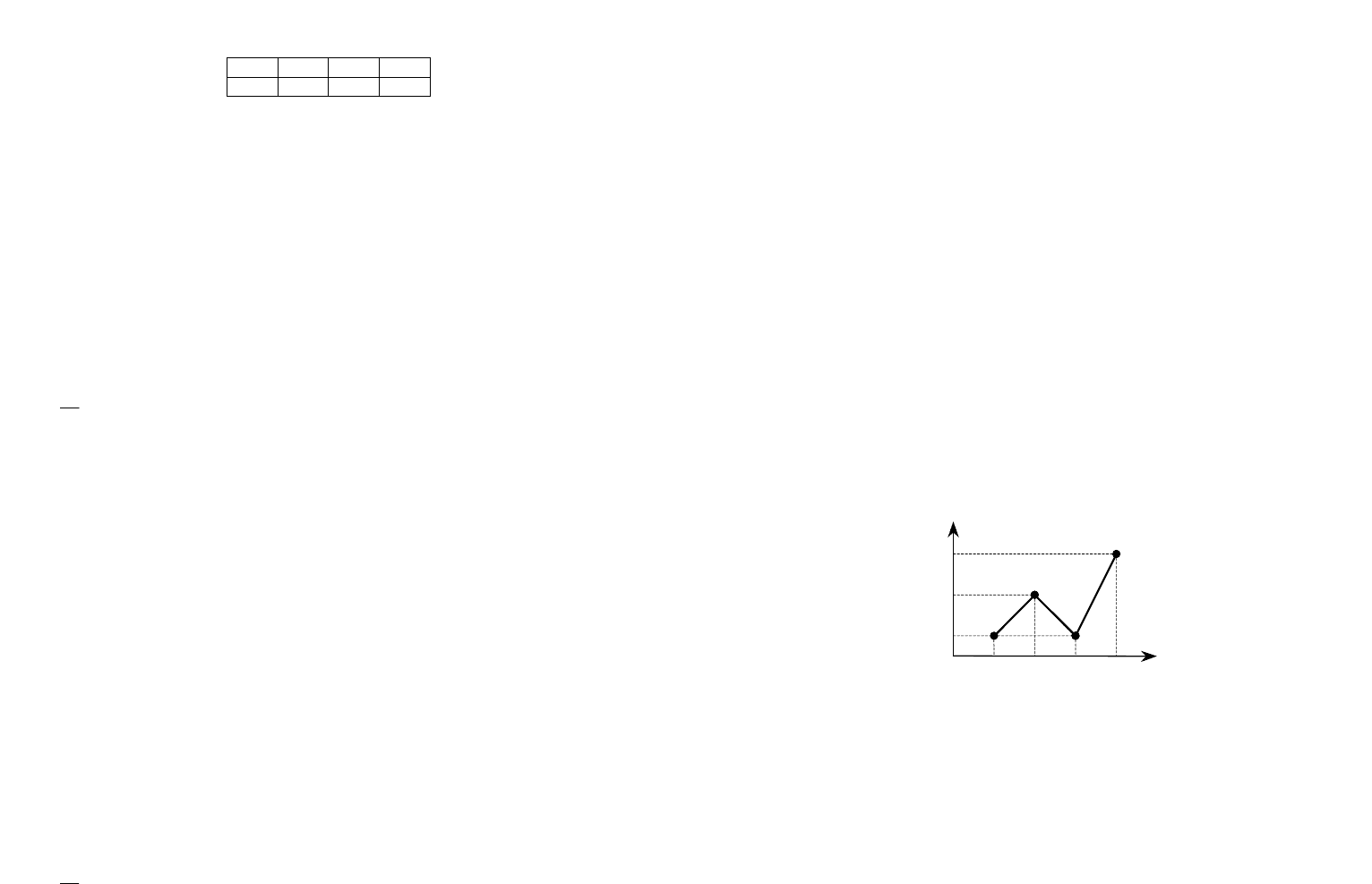
ВАРИАНТ 30

12. Дискретная случайная величина X задана законом распределения:

3 5

0,5 0,2 0,3

Если известно, что ее математическое ожидание M(X) равно 3,1, то x

равно:

A) 2;

B) 1;

C) 0;

D) – 1.

13. Найти дисперсию случайной величины Z = 3X – Y + 2, если известны дисперсии

независимых случайных величин X и Y: D(X) = 1, D(Y) = 3.

A) 6;

B) 8;

C) 2;

D) 12.

14. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.5при1

;50при

0;при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (3, 6).

A) 16/25;

B) 3/25;

C) 8/25;

D) 12/25.

15. Дана дифференциальная функция случайной величины X:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.1при0

;10при2

;0при0

Найти вероятность того, что в результате испытания X примет значение, заключенное в

интервале (0,4; 0,8).

A) 0,12;

B) 0,25;

C) 0,75;

D) 0,48.

16. Случайная величина X задана интегральной функцией:

()

⎪

⎩

⎪

⎨

⎧

≤<

≤

.6при1

;60при

0;при0

Математическое ожидание X равно:

A) 3;

B) 4;

C) 16/9;

D) 20/9.

17. Найти моду статистической выборки: 7, 4, 3, 1, 3, 4, 7, 4, 1, 2.

A) 7;

B) 4;

C) 3;

D) 1.

18. Если основная гипотеза имеет вид H

: a = 9, то конкурирующей может быть

гипотеза:

A) Н

: a ≤ 9;

B) Н

: a ≥ 9;

C) Н

: a > 9;

D) Н

: a ≠ 8.

19. Точечная оценка математического ожидания случайной величины, распределенной

по нормальному закону, равна 13. Тогда его интервальная оценка может быть записана

в виде:

A) (11; 14);

B) (12; 15);

C) (13; 14);

D) (12,6; 13,4).

20. Из генеральной совокупности извлечена выборка объема n = 30, полигон

относительных частот которой имеет вид

10 15 20

Тогда число вариант x

= 15 в выборке равно:

A) 3;

B) 5;

C) 6;

D) 10;

21. Выборочное уравнение парной регрессии имеет вид y = – 2x + 2. Тогда выборочный

коэффициент корреляции может быть равен:

A) – 2;

B) – 0,75;

C) 0;

D) 2.