Леонов Г.А., Шумафов М.М. Проблемы стабилизации линейных управляемых систем
Подождите немного. Документ загружается.

41
некоторый периодический сигнал вида
y(t) = A(iω)e
i(ωt)+iα(iω )
— переменный ток амплитуды A( iω) той же частоты ω, что и при
входе, но по фазе сдвинутый на α(iω). Из (23) следует, что будут
иметь место приближенные равенства
A(iω) ˙=|W (iω)|, α(iω) ˙=arg W (iω). (24)
По формулам (24) однозначно определяется комплексное число
W (iω). Затем, прогоняя ω от −∞ до +∞, получим годограф W (iω)
на комплексной плоскости. На самом деле, из-за очевидного равен-
ства
lim
ω→+∞
W (iω) = 0,
эту прогонку следует проводить только на конечном промежутке из-
менения ω.
Таким образом, для получения указанным путем частотной ха-
рактеристики не нужно информации о матрице A и векторах b и c,
а в уравнении (14) о коэффициентах многочленов N(p) и M (p). По-
скольку многие результаты в теории управления формулируются в
терминах частотных характеристик, то для них не требуется описа-
ние соответствующих линейных блоков (L) системами дифференци-
альных уравнений, а нужна только кривая — годограф частотной
характеристики на комплексной плоскости.
Отметим, что в силу принципа аналитического продолжения ча-
стотная характеристика W (iω) позволяет однозначно определить и
передаточную функцию W (p).

42
ГЛАВА II
УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ
§1. Управляемость
Пусть объект управления описывается линейной системой
˙x = Ax + bu, y = c
∗
x, (1)
где A, b, c — вещественные постоянные матрицы порядков n × n,
n ×m, n ×l соответственно, x = x(t), u = u(t), y = y(t) — векторные
функции соответственно порядков n, m, `: x ∈ R
n
, u ∈ R
m
, y ∈ R
`
.
Для фиксированного t ∈ [t
0
, T ] (t
0
< T ) вектор x = x(t) будем на-
зывать состоянием системы, вектор u = u(t) — входом или управле-
нием, вектор y = y(t) — выходом. Точка над символом x обозначает
дифференцирование по t.
Проблема управления состоит в выборе функции u(t) таким об-
разом, чтобы перевести объект из любого состояния в фазовом про-
странстве в любое другое состояние за наперед заданное время.
Пример. Пусть материальная точка движется вдоль оси x под
действием силы f(t). Требуется выбрать силу f(t) так, чтобы точка,
занимающая в начальный момент времени положение x
0
и имеющая
скорость ˙x
0
, через время T остановилась в заданном положении.
Примем заданное положение, где материальная точка должна оста-
новиться, за начало координат. Обозначим через x(t) координату ма-
териальной точки в момент времени t.
Математическая формулировка задачи такова: найти функцию
f(t), t ∈ [0, T ], удовлетворяющую условиям:
m¨x(t) = f(t),
x(0) = x
0
, ˙x(0) = ˙x
0
; x(T ) = 0, ˙x(T ) = 0.
)
(2)
(Здесь m — масса материальной точки).
Введя обозначения x
1
= x, x
2
= ˙x, u =
1
m
f, перейдем к эквива-
лентной системе
˙x
1
= x
2
, ˙x
2
= u,
x
1
(0) = x
0
, x
2
(0) = ˙x
0
; x
1
(T ) = 0, x
2
(T ) = 0.

43
Интегрируя уравнения движения, имеем
x
2
(t) = ˙x
0
+
t
Z
0
u(s) ds,
x
1
(t) = x
0
+ ˙x
0
t +
t
R
0
µ
τ
R
0
u(s) ds
¶
dτ.
Из условий x
1
(T ) = 0, x
2
(T ) = 0 получаем уравнения (интегральные)
для определения u(t):
T
Z
0
u(s) ds = −˙x
0
;
T
Z
0
τ
Z
0
u(s) ds
dτ = −x
0
− T ˙x
0
.
Будем искать u(t) в виде
u(t) = d
0
t + d
1
,
где d
0
и d
1
— неопределенные коэффициенты, подлежащие опреде-
лению. Подставляя это выражение в последние два интегральные
уравнения, получим алгебраическую систему двух линейных урав-
нений относительно d
0
и d
1
T
2
2
d
0
+ T d
1
= −˙x
0
,
T
3
6
d
0
+
T
2
2
d
1
= −x
0
− T ˙x
0
.
Отсюда
d
0
=
12
T
3
µ
x
0
+
T
2
˙x
0
¶
,
d
1
= −
6
T
2
µ
x
0
+
2
3
T ˙x
0
¶
.
Найденное управление u(t) решает поставленную задачу (2).
Отметим, что сложность проблемы управляемости состоит в том,
что число управлений (размерность m вектора u), как правило, мень-
ше числа управляемых процессов (размерности n вектора x).
Дальше мы дадим определение полной управляемости системы (1)
и докажем теорему о необходимых и достаточных условиях полной
управляемости.
44
О п р е д е л е н и е 1. С и с т е м а (1) называется п о л н о-
с т ь ю у п р а в л я е м о й (или п а р а (A, b) называется
п о л н о с т ь ю управляемой), если для любых векторов x
0
∈ R
n
,
x
1
∈ R
n
и любых t
0
< t
1
существует такое управление u(t) (яв-
ляющееся кусочно-непрерывной функцией, заданной на [t
0
, t
1
]), что
для решения x(t) системы (1) с этим управлением и с начальным
условием x(t
0
) = x
0
выполнено равенство x(t
1
) = x
1
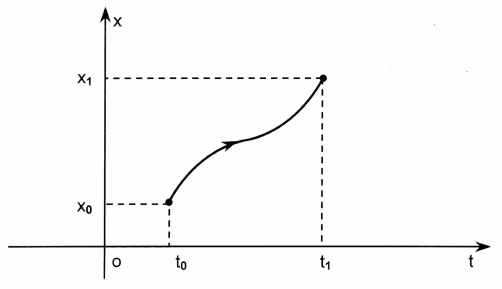
(рис. 3).
Можно дать и такое определение полной управляемости системы.
О п р е д е л е н и е 1
0
. С и с т е м а (1) называется п о л н о-
с т ь ю у п р а в л я е м о й (п а р а (A, b) называется п о л н о с-
т ь ю у п р а в л я е м о й ), если для любого T > 0 и любого вектора
x
0
∈ R
n
существует такое управление u(t) (являющееся кусочно-
непрерывной функцией, заданной на [0, T ]), что для решения x(t)
системы (1) с этим управлением и с начальным условием x(0) = x
0
выполнено равенство x(T ) = 0.
Рис. 3. Решение x(t) полностью управляемой системы
x(t
0
) = x
0
, x(t
1
) = x
1
∀t
0
, t
1
∈ R и ∀x
0
, x
1
∈ R
n
Определение 1 эквивалентно определению 1
0
в силу линейности и
стационарности системы (1) ( правая часть не зависит явно от t).
Действительно, пусть система (1) управляема в смысле опреде-
ления 1
0
, и пусть t
0
, t
1
— любые числа, а x
0
, x
1
— любые векторы
из R
n
. Тогда существуют управления ¯u(t) и ˜u(t) такие, что для со-
ответствующих решений ¯x(t) и ˜x(t) системы (1) будут выполнены
45
равенства
¯x(0) = x
0
, ¯x(T ) = 0,
˜x(0) = 0, ˜x(T ) = x
1
,
где T = t
1
− t
0
.
Так как правая часть системы (1) не зависит явно от t, то сдвиг
любого её решения вдоль оси t есть снова решение. Следовательно,
вектор-функция x(t) = ¯x(t − t
0
) + ˜x(t − t
0
) будет решением системы
(1), удовлетворяющим условиям x(t
0
) = x
0
, x(t
1
) = x
1
с соответству-
ющим управлением u(t) = ¯u(t − t
0
) + ˜u(t −t
0
), т.е. система (1) будет
управляема в смысле определения 1. Обратное очевидно.
Итак, система (1) полностью управляема, если его вектор состоя-
ния x(t) за счет подаваемого на вход управления u(t) можно переве-
сти из произвольного начального состояния x
0
в начало координат
за любое конечное время.
Заметим, что всюду ниже, не оговаривая это особо, будем счи-
тать, что пространство R
n
и линейные операторы, определяемые ве-
щественными матрицами A, b и c соответственно, комплексифициро-
ваны (см. § 2, гл.I). При этом комплексифицированное пространство
CR
n
мы обозначаем через C
n
.
Теорема. (О критериях полной управляемости [54, 95].)
Следующие условия эквивалентны между собой и каждое из них
является необходимым и достаточным условием для полной управ-
ляемости системы (1):
(I
y
) Ранг матрицы
R = (b, Ab, . . . , A
n−1
b) (3)
порядка n × mn равен n:
rank (b, Ab, . . . , A
n−1
b) = n
или, иначе, соотношения
z
∗
A
k
b = 0 (k = 0, 1, . . . , n − 1) (4)
для вектора z ∈ R
n
могут быть выполнены лишь для z = 0.
(II
y
) Пусть Ω — произвольное множество плоскости комплекс-
ного переменного, включащее хотя бы одну свою предельную точку.
Соотношение
z
∗
e
pA
b = 0 ∀p ∈ Ω, (5)
46
где z ∈ C
n
, влечет z = 0.
(II
0
y
) Для любых чисел t
1
< t
2
соотношение
z
∗
e
At
b = 0 ∀t ∈ (t
1
, t
2
), (6)
где z ∈ R
n
, возможно лишь для z = 0.
(III
y
) Пусть Ω — произвольное множество плоскости комплекс-
ного переменного p, включающее хотя бы одну свою предельную точ-
ку и не содержащее собственных значений матрицы A.
Соотношение
z
∗
(pI − A)
−1
b = 0 (∀p ∈ Ω), (7)
где z ∈ C
n
, возможно лишь для z = 0 (здесь I — единичная (n ×n)-
матрица).
(III
0
y
) Пусть (t
1
, t
2
) ⊂ R — произвольный интервал веществен-
ной оси. Соотношение
z
∗
(pI − A)
−1
b = 0 (∀p ∈ (t
1
, t
2
)),
где z ∈ R
n
, возможно лишь для z = 0.
(IV
y
) Ранг матрицы (d
0
, . . . , d
n−1
) (порядка n × nm), где d
i
(i = 0, . . . , n −1) — вещественные (n ×m)-матрицы–коэффициенты
многочлена
¡
det(pI − A)
¢
(pI − A)
−1
b = d
n−1
p
n−1
+ . . . + d
0
, (8)
равен n.
(V
y
) Для любых чисел t
1
< t
2
симметрическая матрица
K =
t
2
Z
t
1
e
At
bb
∗
e
A
∗
t
dt. (9)
является положительно определенной (соответствующая квадра-
тичная форма z
∗
Kz > 0 ∀z ∈ R
n
, z 6= 0).
(V I
y
) Соотношения A
∗
z = pz, z
∗
b = 0, выполненные для какого-
либо числа p
0
∈ C и вектора z ∈ C, возможны лишь для z = 0, т.е.
не существует ненулевого вектора z ∈ C
n
, для которого выполне-
ны равенства A
∗
z = p
0
z, z
∗
b = 0, где p
0
— некоторое комплексное
число.
47
(V II
y
) Для любого комплексного числа p ранг матрицы (A−pI, b)
порядка n × (n + m) равен n.
(V III
y
) Не существует такой неособой вещественной матри-
цы S порядка n × n, что преобразованные матрицы S
−1
AS и S
−1
b
имеют вид
S
−1
AS =
µ
A
11
A
12
0 A
22
¶
ª
n
1
ª
n
2
, S
−1
b =
µ
b
1
0
¶
ª
n
1
ª
n
2
.
|{z}
n
1
|{z}
n
2
(10)
или
S
−1
AS =
µ
A
11
0
A
21
A
22
¶
ª
n
1
ª
n
2
, S
−1
b =
µ
0
b
2
¶
ª
n
1
ª
n
2
.
|{z}
n
1
|{z}
n
2
(11)
(сбоку и внизу указаны размерности матриц).
Д о к а з а т е л ь с т в о. Для того, чтобы установить указанную в тео-
реме эквивалентность условий, достаточно доказать следующую це-
почку импликаций:
(V I
y
) ⇐⇒ (V II
y
) ⇐⇒ (полная управляемость) =⇒
=⇒ (II
y
) ⇐⇒ (II
0
y
) =⇒ (III
y
) ⇐⇒ (IV
y
) =⇒ (I
y
) ⇒
⇒ (V
y
) ⇒ (полная управляемость) ⇐⇒ (V III
y
),
(12)
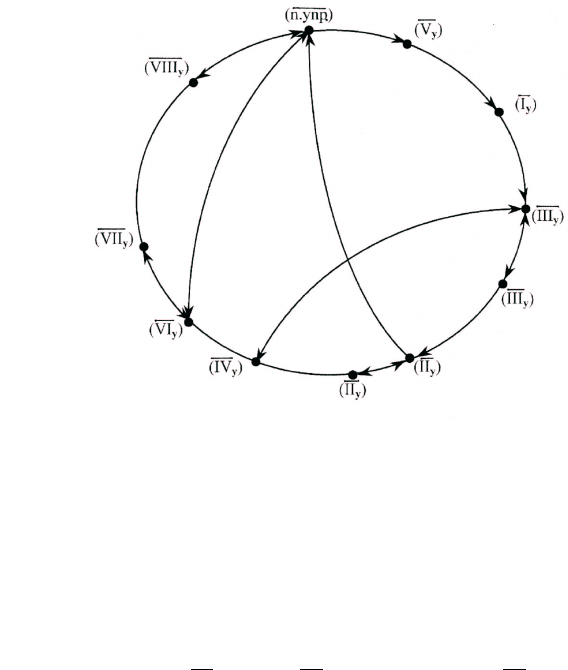
или аналогичную цепочку для отрицания соответствующих утвер-
ждений (см. рис. 4):
(V III
y
) ⇐⇒ (полная управляемость) ⇒ (V
y
) ⇒
⇒ (I
y
) ⇒ (IV
y
) ⇐⇒ (III
y
) ⇒ (II
0
y
) ⇐⇒ (II
y
) ⇒
⇒ (полная управляемость) ⇐⇒ (V I
y
) ⇐⇒ (V II
y
)
(13)
48
Рис. 4. К доказательству теоремы 1.
1. Эквивалентность (V I
y
) ⇐⇒ (V II
y
). Условие (V I
y
) означает,
что равенства
z
∗
(A − ¯pI) = 0, z
∗
b = 0
(при любом фиксированном p ∈ C) выполняются лишь для z = 0
или, что то же самое, соотношение z
∗
(A − ¯pI, b) = 0, возможно лишь
для z = 0, т.е. что ранг матрицы (A − pI, b) равен n для любого p.
2. Эквивалентность (II
y
) ⇐⇒ (II
0
y
). Утверждение (II
y
) означа-
ет, что равенство (5) выполнено для некоторого ненулевого вектора
z
0
∈ C
n
и всех p из некоторого подмножества Ω
0
∈ C комплекс-
ной плоскости, содержащего по крайней мере одну свою предельную
точку:
z
∗
0
(exp pA)b = 0 ∀p ∈ Ω
0
. (14)
Пусть p
0
— предельная точка множества Ω
0
. Тогда существует
последовательность {p
k
} (k ∈ N), p
k
∈ Ω
0
, p
k
6= p
0
, что lim
k→∞
p
k
= p
0
,
причем p
0
∈ Ω
0
. Для произвольного вектора ξ
0
∈ C
m
функция
ϕ(p) = z
∗
0
(exp pA)bξ
0
(15)
49
комплексного переменного p будет, очевидно, аналитической (голо-
морфной) на всей комплексной плоскости C и, поэтому, в силу (14),
обладает свойством
ϕ(p
k
) = 0, (k = 1, 2, . . .), ϕ(p
0
) = 0. (16)
Согласно свойству единственности аналитической функции будем
иметь ϕ(p) ≡ 0 на C. Действительно, разлагая функцию ϕ(p) в сте-
пенной ряд (он сходится везде, так как ϕ(p) не имеет особых точек)
ϕ(p) = d
0
+ d
1
(p − p
0
) + d
2
(p − p
0
)
2
+ . . .
в окрестности точки p
0
, и, учитывая, что d
0
= ϕ(p
0
) = 0, в силу (16)
получим
d
1
(p
k
− p
0
) + d
2
(p
k
− p
0
)
2
+ . . . = 0. (17)
Сокращая на (p
k
− p
0
) и переходя к пределу при k → ∞ (p
k
→
p
0
), из (17) будем иметь: d
1
= 0. Поступая аналогично, получим
последовательно, что d
2
= 0, d
3
= 0, . . .. Следовательно, ϕ(p) = 0
∀p ∈ C. Отсюда, учитывая, что в (15) ξ
0
– произвольный вектор,
получаем
z
∗
0
(exp pA)b = 0 ∀p ∈ C. (18)
В частности, (18) имеет место и на любом интервале (t
1
, t
2
) ⊂ R
вещественной оси R. Поэтому, записав z
0
в виде z
0
= z
1
+iz
2
, z
1
∈ R
n
,
z
2
∈ R
n
, будем иметь
z
∗
1
e
tA
b − iz
∗
2
e
tA
b = 0 ∀t ∈ (t
1
, t
2
).
Отсюда, очевидно, следует, что
z
1
e
tA
b = 0, z
2
e
tA
b = 0 ∀t ∈ (t
1
, t
2
) ⊂ R,
причем z
1
, z
2
∈ R
n
, и либо z
1
6= 0, либо z
2
6= 0. Последние равенства
противоречат соотношению (6), т.е. имеет место (II
0
y
).
Обратная импликация (II
0
y
) ⇒ (II
y
) очевидна.
3. Эквивалентность (III
y
) ⇐⇒ (III
0
y
). Эта эквивалентность до-
казывается совершенно аналогично доказательству предыдущего пунк-
та 2 с введением функции
ϕ(p) = z
∗
(pI − A)
−1
b, p ∈ C\{λ
j
(A)},
где z ∈ C
n
, λ
j
(A) (j = 1, ··· , n) — собственные значения матрицы A.

50
4. Импликация (II
y
) ⇒ (полная управляемость) ≡ (п.упр.). Как
было выше показано (см. п.2), утверждение (II
y
) влечет равенство
(18). Пусть x
0
, x
1
∈ R
n
— произвольные векторы, а x(t) — решение
первого уравнения системы (1) с начальным условием x(t
0
) = x
0
.
Тогда по формуле Коши
x(t) = e
A(t−t
0
)
x
0
+
t
1
Z
t
0
e
A(t−s)
bu(s) ds.
Из условия x(t
1
) = x
1
находим
x
1
− e
A(t
1
−t
0
)
x
0
=
t
1
Z
t
0
e
A(t
1
−s)
bu(s) ds.
Отсюда, с учетом (18), получаем, что для любого управления u(t)
z
∗
0
(x
1
− e
A(t
1
−t
0
)
x
0
) =
t
1
Z
t
0
z
∗
0
e
A(t
1
−s)
bu(s) ds = 0,
где, по условию, z
0
6= 0. Равенство
z
∗
0
(x
1
− e
A(t
1
−t
0
)
x
0
) = 0
означает, что вектор x
1
, получаемый для всевозможных управлений
u(t), должен лежать в гиперплоскости
z
∗
0
x = z
∗
0
e
A(t
1
−t
0
)
x
0
,
и, тем самым, не может быть любым. А это противоречит свой-
ству полной управляемости системы (1). Таким образом, (II
y
) ⇒
( п.упр.).
5. Импликация (III
y
) ⇒ (II
y
). Пусть имеет место (III
y
), т.е. не
выполнено соотношение (7). Это означает, существует такой нену-
левой вектор z
0
∈ C
n
, что для некоторого множества Ω
0
⊂ C, со-
держащего хотя бы одну свою предельную точку и не содержащего
собственных значений матрицы A, выполнено соотношение
z
∗
0
(pI − A)
−1
b = 0 ∀p ∈ Ω
0
. (19)
Рассматривая функцию комплексного переменного
ψ(p) = z
∗
0
(pI − A)
−1
bξ
0
,
