Малхорта, Нэреш К. Маркетинговые исследования. Практическое руководство

Подождите немного. Документ загружается.

Среди мужчин до 45 лет 60% изъявили желание отправиться в турпоездку заграницу, а по-

сле 45 лет — всего лишь 40%. Обратная ситуация наблюдалась для женщин: в возрасте до 45 лет

желающих отправиться посмотреть мир оказалось 35%, а после 45 лет — 65%. Поскольку связь

между желанием путешествовать и возрастом различна для мужчин и женшин и с противопо-

ложной направленностью, связь между этими двумя переменными была скрыта, пока данные

не учитывали переменную

"пол",

как это сделано в табл. 15.10. Но при проверке влияния пола,

как показано в табл. 15.11, проигнорированная связь между желанием путешествовать и воз-

растом была обнаружена для отдельных категорий: мужчин и женшин.

Никаких

изменении

в первоначальной связи. В некоторых случаях третья переменная не из-

меняет первоначально наблюдаемую связь, независимо от того, были ли исходные переменные

взаимосвязаны. Это означает, что третья переменная никак не влияет на связь между двумя

первыми переменными. Рассмотрим

кросс-табуляцию

двух переменных: размер семьи и часто-

ту посещения ресторанов быстрого питания, представленную в табл.

15.12.

Таблица 15.12. Связь частоты посещения ресторанов быстрого питания с размером

семьи

Частота

посещения

ресторана

быстрого

питания

Большая

Маленькая

Итого

Число респондентов

Небольшая

65%

35%

100%

500

Размер семьи

Большая

65%

35%

100%

500

Респондентов разделили (используя медиану) на две равные по размеру категории по 500

респондентов в каждой: небольшая и большая семья, Не наблюдалось никакой связи, Затем по

этому же принципу респондентов разделили на категории: семьи с большим и малым доходом.

При введении в анализ третьей переменной получили табл.

15,13.

И снова не наблюдалось ни-

какой

связи.

Таблица

15.13.

Связь частоты посещения ресторанов быстрого

питания

с размером

семьи и уровнем дохода

Доход

Семьи с

низким

доходом Семьи с высоким доходом

Частота

посещения ресторанов быстрого питания Малая Большая Малая Большая

Большая

Маленькая

Итого

Число респондентов

65%

35%

100%

250

65%

35%

100%

250

65%

35%

100%

250

65%

35%

100%

250

Общие комментарии по поводу кросс-табуляции

Можно построить

таблицу

сопряженности больше, чем для трех переменных, но интер-

претация полученных результатов достаточно сложная. Кроме того, поскольку число ячеек

многократно увеличится, проблематично оставить необходимое количество респондентов

или случаев в каждой ячейке. Как правило, чтобы вычислить статистику в каждой ячейке,

должно быть, по крайней мере, пять наблюдений. Таким образом, кросс-табуляция — не-

эффективный

способ проверки связей для ситуаций с несколькими переменными, она рас-

574 Часть III. Сбор, подготовка и анализ данных

сматривает

просто связь между переменными, а не причинность. Чтобы изучить причинно-

следственную связь, необходимо провести соответствующее причинно-следственное иссле-

дование (см. главу 7).

СТАТИСТИКИ ТАБЛИЦ СОПРЯЖЕННОСТИ

ПРИЗНАКОВ

Мы рассмотрим статистики, обычно используемые для оценки статистической значимости

и тесноты связи переменных,

содержащихся

в таблице сопряженности. Статистическая значи-

мость наблюдаемой связи обычно измеряется критерием

хи-квадрат.

Теснота связи важна с

практической точки зрения. Обычно она имеет значение, если связь статистически значимая.

Тесноту связи можно измерить коэффициентом корреляции фи, коэффициентом сопряжен-

ности

признаков,

У-коэффициентом

Крамера и коэффициентом "лямбда". Эти статистики

ниже описаны детальнее.

Критерий хи-квадрат

(chi-square

statistic,

)

используют для проверки статистической зна-

чимости наблюдаемой связи в таблице сопряженности признаков.

Критерий хи-квадрат

(chi-square

statistic,

%2)

Критерий,

используемый для проверки статистической значимости наблюдаемых связей в

таблицах

сопряженности

признаков. Он помогает определить наличие или отсутствие сис-

тематической связи между двумя переменными.

Он помогает определить наличие или отсутствие систематической связи между двумя пере-

менными. В данном случае нулевая гипотеза

утверждает, что между двумя переменными не

существует никакой связи. Проверка нулевой гипотезы выполняется вычислением частот рас-

пределения признаков анализируемых переменных в ячейках таблицы, которые можно было

бы ожидать, если бы не существовало зависимости между переменными, и при данных итого-

вых числах в каждом ряду и колонке. Затем для вычисления значения

эти

ожидаемые часто-

ты,

обозначаемые

сравнивают с фактически наблюдаемыми частотами распределения при-

знаков/о,

соответствующими ячейкам таблицы. Чем больше разница между ожидаемыми и

фактическими частотами, тем выше значение статистики. Предположим, что таблица сопря-

женности имеет

рядов и с колонок, а случайная выборка состоит из

наблюдений. Тогда

ожидаемую частоту для каждой ячейки вычислим по следующей формуле:

- '

где

п, — итоговое число в ряду,

— итоговое число в колонке, л — полный размер выборки.

Для данных табл. 15.3 ожидаемая частота распределения признаков для ячеек, расположен-

ных слева направо и сверху

вниз,

выглядит так:

30 30

7,50;

15X15.7.50.

30 30

Тогда значение

вычисляют следующим образом:

Глава 15. Вариационный

ряд,

таблицы сопряженности признаков и проверка гипотез 575

Для данных табл.

15.3

значение

вычислили по формуле:

(5-7,5)'

;

(10-7,5)*

(10-7,5)

(5-7.5)

7,5 7,5 7,5 7,5

= 0,833 + 0,833+0,833 + 0,833

= 3,333

Чтобы определить, существует ли между переменными систематическая связь, определяют

вероятность получения значения

равного или большего, чем рассчитанное из таблицы со-

пряженности. Важной характеристикой критерия

является число степеней свободы

(df).

обшем случае оно равно числу наблюдений за вычетом числа ограничений, необходимых для

вычисления статистического показателя. Для критерия

хи-квадрат

таблицы

сопряженности

число степеней свободы равно произведению количества рядов (

) минус единица на количе-

ство

колонок

( с ) минус единица, т.е. df

=(г-1)х(с-1)

[11].

Нулевая гипотеза

(Я

)

об отсутст-

вии зависимости между двумя переменными должна быть отклонена только тогда, когда полу-

ченное значение

больше,

чем критическое значение

распределения с соответствующим

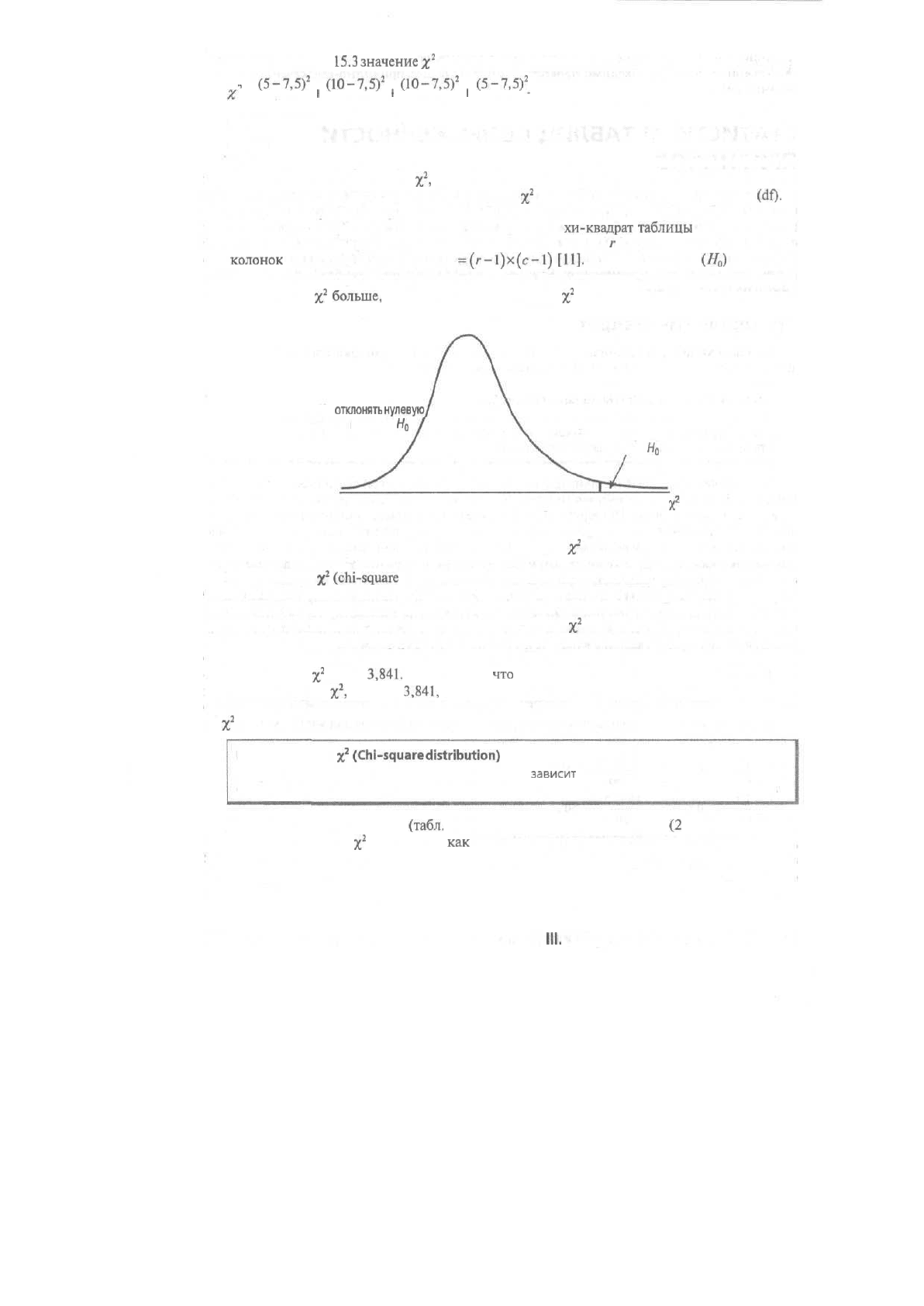
числом степеней свободы, как это показано на рис. 15.8.

Не

отклонять

нулевую;

гипотезу

Отклонить нулевую

гипотезу

Критическое значение

'1,

Рис. 15.8. Проверка зависимости между переменными

с помощью критерия

у}

Распределение

(chi-square

distribution) представляет собой асимметричное распределение,

форма которого зависит исключительно от числа степеней свободы [12]. С ростом числа степе-

ней свободы распределение хи-квадрат становится более симметричным. Данные табл. 3 в Ста-

тистическом приложении дают представление о величине

Для различных степеней свободы.

В этой таблице значение вверху каждой колонки указывает область в верхней части (правая

сторона на рис. 15,8) распределения хи-квадрат. Например, для одной степени свободы и

а = 0,05 значение

равно

3,841.

Это означает,

что

для одной степени свободы вероятность пре-

вышения значения

равного

3,841,

составляет 0,05. Другими словами, при уровне значимо-

сти, равном 0,05, и числе степеней свободы, равном единице, критическое значение статисти-

ки

равно 3,841.

Распределение

(Chi-square

distribution)

Асимметричное распределение, форма которого

зависит

исключительно от числа степеней

свободы. С ростом числа степеней свободы хи-квадрат распределение более симметрично,

Для таблицы сопряженности

(табл.

15.3) число степеней свободы равно

— 1) х (2 — 1) = 1.

Вычисленное значение

— 3,333. Так

как

оно меньше критического значения, равного 3,841,

нулевую гипотезу об отсутствии связей между переменными нельзя отклонить. Это означает,

что связь между переменными не является статистически значимой при уровне значимости,

равном 0,05.

576 Часть

lit.

Сбор, подготовка и анализ данных

Статистику

хи-квадрат

также можно использовать в проверках степени согласия, чтобы оп-

ределить, согласуется ли определенная модель с наблюдаемыми данными. Эти проверки вы-

полняют вычислением значимости (уровня статистической значимости) выборочных отклоне-

ний от предполагаемых теоретических (ожидаемых)

распределений,

а также можно выполнить

как на основе таблиц сопряженности, так и на основе таблиц распределения частот

(одномерная табуляция). Расчет

и определение ее уровня статистической значимости вы-

полняется изложенным выше способом.

Значение

•£

следует вычислять только для числовых данных. Если данные представлены в

виде процентов, то сначала их необходимо перевести в абсолютные единицы или числа. Кроме

того, допущение,

лежащее

в основе проверки с помощью критерия

у?,

заключается в том, что

наблюдения проведены независимо. В качестве общего правила стоит запомнить, что проверку

по критерию хи-квадрат нельзя выполнять, если ожидаемые или теоретические частоты в лю-

бой из ячеек меньше пяти. Если число наблюдений в любой ячейке меньше

десяти,

или если

таблица имеет два рядка и две колонки (таблица 2 х 2), то необходимо использовать поправоч-

ный коэффициент [13]. С поправочным коэффициентом значение

равно 2,133, что не явля-

ется значимым при уровне значимости, равном 0,05. Для таблицы размером

2x2,

статистику

хи-квадрат называют

фи-коэффициентом.

Фи-коэффициент

Фн-коэффициент

(phi coefficient,

ф)

используют для измерения тесноты связи в особом слу-

чае — при анализе таблицы с двумя рядками и двумя колонками (таблица 2 х 2).

Фи-коэффициент

(phi

coefficient,

ф)

Мера тесноты связи

переменных

для конкретного вида таблицы: с двумя рядками и двумя

колонками (таблица 2 х 2).

Фи-коэффициент пропорционален корню квадратному из

Для выборки размером

эту

статистику находят по формуле:

Фи-квадрат

принимает значение, равное 0, если связь отсутствует, на что также указывает и

значение хи-квадрат, равное 0. При сильной связи между переменными фи-коэффициент

имеет значение 1 и все наблюдения находятся на главной или второстепенной диагонали. (В

некоторых компьютерных программах фи-коэффициент принимает значение

—1,

а не +1, ко-

гда наблюдается отрицательная связь.) В нашем случае фи-коэффициент равен:

Таким образом, связь не очень сильна. В более общем случае при наличии таблицы любого

размера тесноту связи можно оценить коэффициентом сопряженности признаков.

Коэффициент сопряженности признаков

Фи-коэффициент применяют только к таблице 2 х 2, а коэффициент сопряженности

признаков С

(contingency

coefficient) используют для оценки тесноты связи в таблицах лю-

бого размера.

Коэффициент сопряженности признаков (contingency coefficient)

Мера тесноты связи в таблицах любого

размера.

Глава

15. Вариационный ряд, таблицы сопряженности признаков и проверка гипотез 577

Коэффициент сопряженности признаков связан с

следующим

образом:

f-i

___ I

Vr+«

Значения коэффициента сопряженности находятся в диапазоне от 0 до 1. При отсутствии

связи он равен нулю (т.е. переменные статистически независимы), но своего максимального

значения

(1) он никогда не достигает. Максимальное значение коэффициента сопряженности

зависит от размера таблицы (числа рядков и колонок). Поэтому он используется только для

сравнения таблиц одинакового размера. Значение коэффициента сопряженности для табл. 15.3

следующее:

3,333+ 30

Это

значение

коэффициента сопряженности указывает на слабую связь. Другой статистикой,

которую можно вычислить для любой таблицы, является

К-козффициент

Крамера (Cramer).

И-коэффициент

Крамера

К-коэффициент

Крамера (Cramer's V) — это модифицированная версия коэффициента кор-

реляции фи

), которую используют в таблицах, больших по размеру, чем

2x2.

V-коэффициент

Крамера (Cramer's V)

Мера тесноты связи,

используемая

в таблицах, больших по размеру, чем

2x2.

Если для таблиц, больших, чем

2x2,

вычисляют фи-коэффициент, то он не имеет верхней

границы.

К-коэффициент

Крамера получают корректировкой

фи-коэффициента

или по числу

рядов, или по числу колонок в таблице. Причем из двух значений выбирают меньшее. Коррек-

тировку

осуществляют

так, что значения

К-коэффициента

лежат в диапазоне от 0 до 1. Большее

значение

К-коэффициента

указывает на более сильную связь, но не указывает, как связаны пе-

ременные. Для таблицы с

рядами и с колонками связь между

К-коэффициентом

Крамера и

фи-коэффициентом

выражается следующим образом:

Значение V-коэффициент Крамера для табл. 15.3 равно:

Таким образом, связь не очень сильна. В этом случае V =

. Так всегда происходит для таб-

лицы

2x2.

Другой обычно рассчитываемой статистикой является коэффициент "лямбда".

Коэффициент

"лямбда

Коэффициент "лямбда" используется в том случае, когда переменные измерены с помо-

щью номинальной шкалы.

Асимметрический

коэффициент

"лямбда"

(asymmetric lambda) по-

казывает выраженное в процентах улучшение при прогнозировании значения зависимой пе-

ременной при данном значении независимой переменной,

I—

Асимметрический коэффициент "лямбда" (asymmetric lambda)

Мера

выраженного

в процентах улучшения прогнозирования значения зависимой перемен-

ной при данном значении независимой переменной. Значения коэффициента "лямбда" ле-

жат в пределах от 0 до

578 Часть III. Сбор, подготовка и анализ данных

Значения коэффициента "лямбда" лежат в пределах от 0 до 1. Значение "лямбда", равное О,

означает, что никакого улучшения в прогнозировании не наблюдается. Значение 1 указывает

на то, что прогноз может быть сделан без ошибки. Это происходит тогда, когда каждая катего-

рия независимой переменной связана с одной категорией зависимой

переменной.

Асимметрический коэффициент "лямбда" подсчитывают для каждой из зависимых пере-

менных. Также рассчитывают симметричный коэффициент

"лямбда"

(symmetric lambda) —

средним значением двух асимметричных значений.

Симметричный коэффициент "лямбда" (symmetric lambda)

Симметричный коэффициент "лямбда" не дает предположения о

том,

какая из переменных

зависимая. Он измеряет общее улучшение прогнозирования, когда прогноз уже сделан в

обоих направлениях.

Симметричный коэффициент "лямбда" не делает предположения о том, какая из пере-

менных зависимая. Он измеряет

общее

улучшение,

прогнозирования, когда прогноз уже

выполнен в обоих направлениях [14]. Значение асимметричного коэффициента "лямбда" в

табл. 15.3, если в качестве

зависимой

переменной взять

использование

Internet, равно 0,333.

Это указывает на то, что знание пола

увеличивает

нашу возможность прогнозирования на

0,333, т.е. имеет место улучшение прогнозирования на 0,33%. Симметричный коэффициент

"лямбда" также равен 0,33%.

Другие статистики

Обратите внимание, что при вычислении значения

у.

переменные должны быть изме-

рены по номинальной шкале. Для измерения связи между двумя порядковыми перемен-

ными применяют другие статистики, такие как may

may с и гамма. Все эти статистики

используют информацию об упорядочении категорий переменных, рассматривая каждую

возможную пару случаев в таблице, чтобы определить, имеет ли первая переменная тот же

относительный порядок расположения (ранг), что и вторая (конкордатное, согласованное

расположение),

или их расположения (ранги) имеют обратный порядок (несогласованное

расположение),

или их ранги совпадают (связанные ранги). Эти статистики отличаются

только способом обработки рангов. Как тау

Ь,

так и

тау

Ь, корректируют по числу связан-

ных рангов. Тау Ь (tau

больше всего подходит для квадратных таблиц,

которых коли-

чество рядов и колонок равно.

Тау b

(tau

Вычисляемая статистика, которая измеряет связь между двумя порядковыми переменными.

Она

вычисляется

с учетом числа

связанных

рангов, и ее лучше использовать для квадратных

таблиц.

Значения этой статистики лежат в пределах от +1 до

—1.

Таким образом, можно определить

направление (положительное или отрицательное) и силу (насколько близко данное значение

находится к 1) связи. Для прямоугольной таблицы, в которой количество рядов отличается от

количества колонок, следует использовать тау с (tau с).

Тау с

(tau

с)

Вычисляемая

статистика, измеряющая связь между двумя порядковыми переменными. Она

вычисляется с учетом числа связанных рангов, и ее лучше использовать, когда таблица пе-

ременных не квадратна, а прямоугольна.

Статистика

"гамма"

(gamma) не учитывает ни связанные ранги, ни размер таблицы. Зна-

чения гаммы также лежат в пределах от +1 до

—1

и обычно имеет большее числовое значе-

ние,

чем тау b и тау с.

Глава 15. Вариационный

ряд,

таблицы сопряженности признаков и проверка гипотез

579

Статистика "гамма" (gamma)

Вычисляемая статистика, измеряющая связь между двумя порядковыми переменными. Она

не делает поправку на связанные ранги.

Данные табл. 15.3, где

пол—

номинальная переменная, не обрабатывают с помощью по-

рядковых статистик. Все изложенные выше статистики можно

оценить

соответствующими

компьютерными программами для кросс-табуляции. Другие статистики для измерения тесно-

ты связи, а именно: смешанный момент корреляции и неметрическая корреляция, обсуждают-

ся в главе 17.

ПРАКТИКА ПРОВЕДЕНИЯ КРОСС-ТАБУЛЯЦИИ

На практике проведение

кросс-табуляции

полезно вести по следующим этапам.

1. Проверьте нулевую гипотезу о том, что отсутствует связь между переменными, используя

критерий

хи-квадрат.

Если вам не удалось отклонить нулевую

гипотезу,

то связь между пе-

ременными отсутствует.

2. Если нулевая гипотеза

Н„

отклонена, то определите тесноту связи, используя

подходящие

статистики

(фи-коэффициент,

коэффициент сопряженности,

К-коэффициент

Крамера,

коэффициент "лямбда" или другие статистики).

3. Если нулевая гипотеза

отклонена, то поясните характер связи, вычислив проценты в

направлении независимой переменной через зависимую переменную.

4. Используйте в качестве проверяемых статистик тау Ь ,

тау

с или "гамму" для обработки

порядковых, а не номинальных переменных. Если нулевая гипотеза

отклонена, то оп-

ределите тесноту связи, используя величину и направление связи, а также учитывая знак

проверяемой статистики.

ПРОВЕРКА ГИПОТЕЗ О РАЗЛИЧИЯХ

В предыдущем разделе проверялись гипотезы о связях между переменными. Теперь мы

сделаем акцент на проверке гипотез о различиях. Классификация процедур проверки гипотез о

различиях

представлена

на рис. 15.9.

Методы, показанные на рис.

15.9,

согласуются с классификацией одномерных методов, пред-

ставленных на рис. 14.6. Главное различие в том, что методы на рис. 14.6 также применимы к не-

скольким выборкам (больше двух) и таким образом связаны с

однофакторным

дисперсионным

анализом (ANOVA) и ранговым дисперсионным анализом

Краскера—Уоллеса

(K-W ANOVA)

(глава 14), тогда как методы на рис, 15.9 ограничены двумя выборками. Процедуры проверки ги-

потез можно в общем виде классифицировать на параметрические и

непараметрические,

исходя

из шкалы измерения переменных. Параметрические методы проверки гипотез (parametric tests)

предполагают, что изучаемые переменные измерены с помощью интервальной шкалы.

Параметрические методы проверки гипотез (parametric tests)

Предполагают, что изучаемые переменные измерены с помощью интервальной шкалы.

Непараметрические методы проверки гипотез

(nonparametric

tests) предполагают, что пере-

менные измерены с помощью номинальной или порядковой шкал.

Непараметрические методы проверки гипотез (nonparametric tests)

Предполагают, что переменные измерены с помощью номинальной или

порядковой

шкал.

580 Часть III. Сбор, подготовка и анализ данных

Проверка гипотезы

Параметрические

методы

проверки

Непараметрические

методы

проверки

аметрические-данные)

(-критерий

z- критерий

Независимые

Двухгрупповой

критерий

I-

критерий

Парные

выборки

Парный

критерий

Критерий

хи-квадрат

Критерий Колмогорова-

Смирнова

Критерий серий

Биномиальный критерий

Критерий

хи-каадрат

Критерий

Манна-Уитни

Медианы

Критерий

Колмогорова-

Смирнова

Парные

выборки

Критерий знаков

Критерий

Вилшксона

Критерий

МакНемара

Критерий

хи-квадрат

Рис. 15.9. Проверка гипотез о различиях

Дальнейшая классификация проводится в зависимости от количества выборок: одна, две

или больше. Как объяснялось в главе 14, число выборок определяют, исходя из метода даль-

нейшей обработки данных для анализа, а не из того, как были собраны данные. Выборки неза-

висимы в том случае, если взяты случайным образом из различных генеральных

совокупностей.

Для анализа данные,

принадлежащие

различным группам респондентов, например мужчинам

женщинам,

обычно обрабатывают как

независимые

выборки. С другой стороны, выборки

являются парными

(связанными),

когда данные двух выборок имеют отношение к одной и той

же группе респондентов.

Наиболее популярный параметрический критерий для проверки гипотез о равенстве сред-

них заключается в расчете значений

/-статистики.

Проверка на основе

/-критерия

выполняется

относительно среднего значения одной или двух выборок. В случае двух выборок они могут

быть независимыми или парными. Непараметрические методы проверки, основанные на на-

блюдениях, взятых из одной

выборки,

включают критерий Колмогорова-Смирнова, критерий

хи-квадрат, критерий серий и биномиальный критерий. В случае двух независимых выборок

для проверки гипотез относительно среднего значения используют

{/-критерий

Манна—Уитни

(Mann—Whitney),

медианный критерий и

двухвыборочный

критерий

Колмогорова—Смирнова.

Эти

критерии—

непараметрические копии

^-критерия

для двух групп. Для парных выборок

непараметрические критерии включают критерий Вилкоксона парных сравнений и критерий

знаков. Эти тесты — копии парного

-критерия. Как

параметрическими,

так и непараметри-

ческими методами

оценивают

гипотезы, относящиеся к более, чем двум выборкам. Эти

крите-

рии рассматриваются в следующих главах.

Глава 15. Вариационный ряд, таблицы сопряженности признаков и проверка

гипотез

581

ПАРАМЕТРИЧЕСКИЕ КРИТЕРИИ

Использование параметрических критериев позволяет

сделать

статистический вывод отно-

сительно среднего значения генеральной совокупности. Обычно для этой цели используют

t-критерий

(t-test). В основе критерия лежит

/-статистика

Стьюдента (Student).

Т-критерий

(t-test)

Одномерный метод проверки гипотез,

использующий

t-распределение.

Применяется, если

стандартное отклонение неизвестно и размер выборки мал.

Т-статистика

(t-statistic)

подразумевает, что переменная нормально распределена, среднее

известно (или предполагается, что оно должно быть известно) и дисперсия генеральной сово-

купности определена по данным выборки.

Т-статистика

{t-statistic)

Статистика, подразумевающая, что переменная имеет

колоколоподобное

распределение,

среднее известно (или предполагается, что известно) и дисперсия генеральной

совокупно-

сти определена

поданным

выборки.

Примем, что случайная переменная

Анормально

распределена, со средним

и неизвестной

дисперсией генеральной совокупности

о"

которая

оценивается

помощью

выборочной дис-

персии s

. Вспомним, что стандартное отклонение выборочного среднего X определяется как

s-f

j/V"

. Тогда / =

(

-,u)/s-

является/-распределенным

л-1

степенями свободы.

Т-распределение

(t-distribution)

по внешнему виду аналогично нормальному распределе-

нию. Графики обоих распределений симметричны и имеют

колоколообразную

форму. Однако

по сравнению с нормальным распределением в распределении Стьюдента хвостовые части гра-

фика по

площади

больше, а центральная часть по площади — меньше.

Это

связано с тем, что

дисперсия совокупности

ет

неизвестна, и ее оценивают во выборочной дисперсии

Т-распределение (t-statistic)

Симметричное колоколоподобное распределение, используемое

для

проверки выборок не-

большого

размера

(п <

30).

При данной неопределенности в значении

наблюдаемые значения

-статистики более

изменчивы, чем значения

г-статистики.

Однако с ростом числа степеней свободы

распределе-

ние приближается к нормальному. Фактически, для выборок большого размера (120 и больше)

t~распределение

нормальное

распределение практически не отличаются. В табл. 4 Статисти-

ческого приложения даны избранные

процентили

/-распределения.

Процедура проверки гипотезы в случае использования в качестве метода проверки

(-критерия

состоит из следующих этапов.

1. Сформулировать нулевую

(Н

)

и альтернативную

(Я,)гипотезы.

2. Выбрать соответствующую формулу для вычисления

/-статистики.

3. Выбрать уровень значимости а для проверки нулевой гипотезы

Обычно выбирают уро-

вень значимости а, равный 0,05.

4. Взять одну или две выборки и для каждой вычислить значение средней и стандартное от-

клонение.

5. Вычислить значение t -статистики, приняв, что нулевая гипотеза ff

верна.

582 Часть

III.

Сбор,

подготовка и анализ данных

6. Вычислить число степеней свободы и

оценить

вероятность получения большего значения

статистики из табл. 4 Статистического приложения. (Альтернативно, вычислить критиче-

ское значение / -статистики).

7. Если вероятность, рассчитанная на этапе 6 меньше, чем уровень значимости

выбран-

ный на этапе 3, то отклонить нулевую гипотезу

Если значение вероятности больше, то

не отклонять. (Альтернативно, если значение, вычисленной на этапе 5

/-статистики,

больше критического значения, определенного на этапе 6, то отклонить нулевую гипотезу

Если вычисленное значение меньше критического значения, то

не следует откло-

нять). Неудачная попытка отклонить нулевую гипотезу необязательно подразумевает, что

верна. Это только означает, что истинное положение несущественно (статистически не-

значимо) отличается от положения, утверждаемого

8. Выразить полученный результат с точки зрения решения проблемы маркетингового ис-

следования.

Мы проиллюстрируем общую

процедуру

проверки гипотез с

помощью

/-критерия

в после-

дующих разделах главы, начав с рассмотрения одной выборки.

Одна выборка

В маркетинговом исследовании аналитика часто интересует утверждение о

сотноше-

нии одной переменной по сравнению с известной или заданной величиной. Примерами

таких утверждений являются: доля рынка для нового товара превышает

15%;

по крайней

мере 65% потребителей понравится новая упаковка; 80% дилеров предпочтут новую поли-

тику ценообразования. Эти утверждения сформулируем с точки зрения нулевой гипотезы,

которую затем

проверим,

используя статистический критерии для одной выборки, такой

как /- или

г-критерий.

Если маркетолог использует

/-критерий

для проверки значения

средней, его интересует, совпадает ли значение генеральной средней со значением, зада-

ваемым в утверждении нулевой гипотезы

(Я

Для данных табл. 15.2 предположим, что

мы хотим проверить гипотезу о том, что среднее значение степени знакомства с Internet

превышает 4,0 (балла) — нейтральное значение по семибалльной шкале. Выберем уровень

значимости,

равный а = 0,05. Сформулируем гипотезы:

:ц<4,0

:ц>4,0

(х-,}

5,385

0,297 О,

ЗУ.'

Число степеней свободы для

/-статистики,

используемой для проверки гипотезы в отноше-

нии среднего значения, равно

~ 1. В нашем случае

— 1 = 29

—

1 или 28. Из табл. 4 Статисти-

ческого приложения находим, что вероятность получения более высокого значения, чем 2,471,

меньше 0,05.

{Альтернативно,

критическое значение

/-статистики

для 28 степеней свободы и

уровня значимости 0,05 равно

1,7011,

что меньше рассчитанного значения, равного 2,471).

Следовательно, нулевую гипотезу отклоняют. Степень знакомства с Internet превышает 4,0,

Обратите внимание, что если нам известно стандартное отклонение генеральной совокуп-

ности, и оно, допустим, равно 1,5, а, значит мы используем его, а не определенное на основа-

нии выборки, то лучше использовать z-критерий

(z-test).

Глава

15.

Вариационный ряд, таблицы сопряженности признаков и проверка гипотез 583