Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.


Extensions
The simplicity of the method suggests that it be tried for comparing the effects
of water-filled pores with clay-filled pores, altered clay grains versus the original
crystalline grain, and so forth.
6.10 Mavko–Jizba squirt relations
Synopsis
The squirt or local flow model suggests that the fluctuating stresses in a rock caused
by a passing seismic wave induce pore-pressure gradients at virtually all scales of
pore-space heterogeneity – particularly on the scale of individual grains and pores.
These gradients impact the viscoelastic behavior of the rock; at high frequencies,
when the gradients are unrelaxed, all elastic moduli (including the shear modulus)
will be stiffer than at low frequencies, when the gradients are relaxed (the latter case
being modeled by Gassmann). Mavko and Jizba (1991) derived simple theoretical
formulas for predicting the very high-frequency moduli of saturated rocks in terms of
the pressure dependence of dry rocks. The prediction is made in two steps: first, the
squirt effect is incorporated as high-frequency “wet-frame moduli” K
uf
and m
uf
, which
are derived from the normal dry moduli as
1
K
uf
1
K
dryhiP
þ
1
K
fl
1
K
0
soft
1
m
uf
1
m
dry
!
¼
4
15
1
K
uf
1
K
dry
where K
uf
is the effective high-frequency, unrelaxed, wet-frame bulk modulus, K
dry
is
the effective bulk modulus of dry rock, K
dry-hiP
is the effective bulk modulus of dry
rock at very high pressure, K
0
is the bulk modulus of the mineral material making up
the rock, K
fl
is the effective bulk modulus of the pore fluid, f
soft
is the soft porosity –
the amount of porosity that closes at high pressure. This is often small enough to
ignore. m
uf
is the effective high-frequency, unrelaxed, wet-frame shear modulus, and
m
dry
is the effective shear modulus of dry rock.
These frame moduli are then substituted into Gassmann’s or Biot’s relations to
incorporate the remaining fluid-saturation effects. For most crustal rocks the amount
of squirt dispersion is comparable to or greater than Biot’s dispersion, and thus using
Biot’s theory alone will lead to poor predictions of high-frequency saturated veloci-
ties. (Exceptions include very high-permeability materials such as ocean sediments
and glass beads; rocks at very high effective pressure when most of the soft, crack-
like porosity is closed; or rocks near free boundaries such as borehole walls.)
297 6.10 Mavko–Jizba squirt relations

A more detailed analysis of the frequency dependence of the squirt mechanism is
presented in Section 6.11.
Although the formulation presented here is independent of any idealized crack
shape, the squirt behavior is also implicit in virtually all published formulations for
effective moduli based on elliptical cracks (see Sections 4.7–4.11). In most of those
models, the cavities are treated as being isolated with respect to flow, thus simulating
the high-frequency limit of the squirt model.
Uses
The Mavko–Jizba squirt relations can be used to calculate high-frequency saturated
rock velocities from dry-rock velocities.
Assumptions and limitations
The use of the Mavko–Jizba squirt relations requires the following considerations:
high seismic frequencies that are ideally suited for ultrasonic laboratory measure-
ments are assumed. In-situ seismic velocities generally will have neither squirt nor
Biot dispersion and should be described using Gassmann’s equations. Sonic-logging
frequencies may or may not be within the range of validity, depending on the rock
type and fluid viscosity;
the rock is isotropic;
all minerals making up the rock have the same bulk and shear moduli; and
fluid-bearing rock is completely saturated.
Extensions
The Mavko–Jizba squirt relations can be extended in the following ways:
for mixed mineralogy, one can usually use an effective average modulus for K
0
;
for clay-filled rocks, it often works best to consider the “soft” clay to be part of the
pore-filling phase rather than part of the mineral matrix. Then the pore fluid is
“mud,” and its modulus can be estimated with an isostress calculation; and
the anisotropic form of these squirt relations has been found by Mukerji and Mavko
(1994) and is discussed in Section 6.14.
6.11 Extension of Mavko–Jizba squirt relations for all frequencies
Synopsis
The Mavko and Jizba (1991) squirt relations (see Section 6.10) predict the very
high-frequency moduli of saturated rocks. At a low frequency, these moduli can
be calculated from Gassmann’s (1951) equations. Dvorkin et al. (1995) introduced
298 Fluid effects on wave propagation
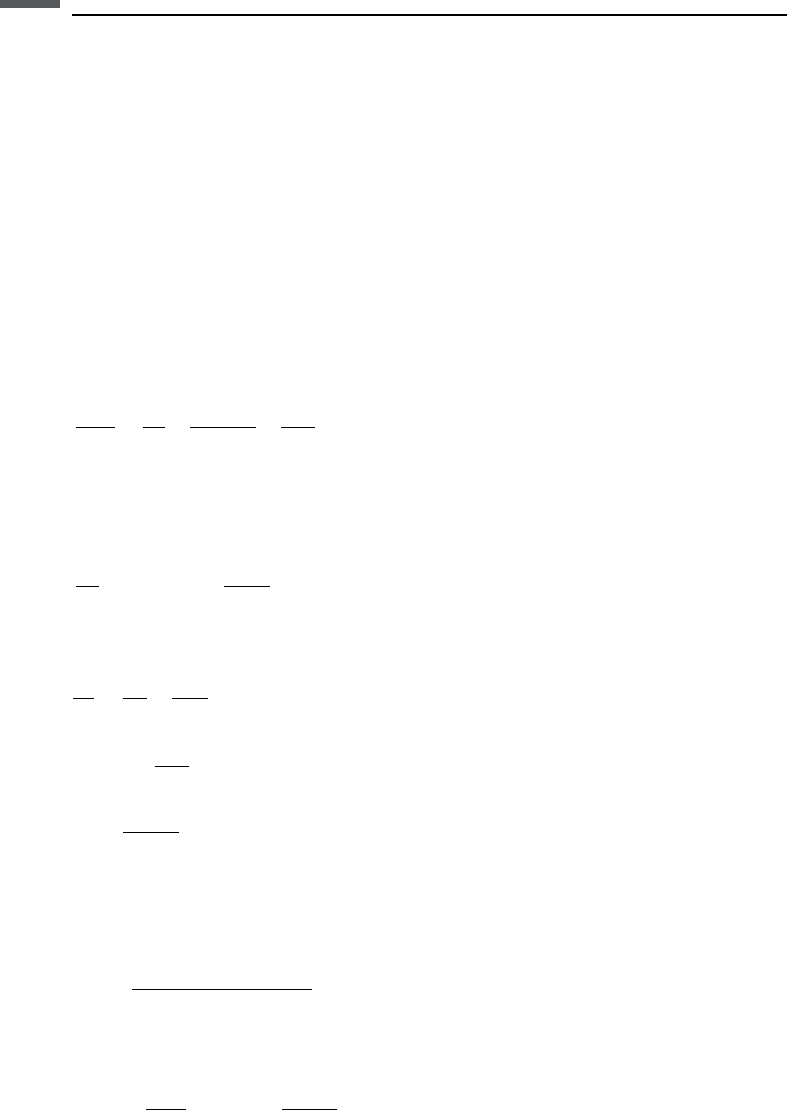
a model for calculating these moduli, velocities, and attenuations at any intermediate
frequency. As input, the model uses such experimentally measurable parameters as
the dry-rock elastic properties at a given effective pressure, the dry-rock bulk
modulus at very high effective pressure, the bulk moduli of the solid and fluid
phases, and the rock density and porosity. One additional parameter (Z), which
determines the frequency scale of the dispersion, is proportional to the characteristic
squirt-flow length. This parameter can be found by matching the theoretical
velocity to that measured experimentally at a given frequency. Then the theory can
be used to calculate velocities and attenuation at any frequency and with any pore
fluid. The algorithm for calculating velocities and attenuation at a given frequency
follows.
Step 1: Calculate the bulk modulus of the dry modified solid (K
msd
) from
1
K
msd
¼
1
K
0
1
K
dryhiP
þ
1
K
dry
Step 2: Calculate the ratio of the induced pore-pressure increment to the confining-
stress increment (dP/ds) from
dP
d
¼ a
0
1 þ
K
dry
a
2
0
F
0
1
where
1
F
0
¼
1
K
fl
þ
1
Q
0
a
0
¼1
K
dry
K
0
Q
0
¼
K
0
a
0
Step 3: Assume a certain value for the frequency-dispersion parameter Z (start with
Z ¼0.001) and calculate the bulk modulus of the saturated modified solid (K
ms
) from
K
ms
¼
K
msd
þ aK
0
½1 f ðxÞ
1 þ af ðxÞdP=d
where
a ¼ 1
K
msd
K
0
; f ðxÞ¼
2J
1
ðxÞ
xJ
0
ðxÞ
; x ¼ Z
ffiffiffiffiffi
io
p
and where o is angular frequency, and J
0
and J
1
are Bessel functions of zero and first
order, respectively.
299 6.11 Extension of Mavko–Jizba squirt relations for all frequencies

Step 4: Calculate the bulk modulus of the modified frame (K
m
) from
1
K
m
¼
1
K
ms
þ
1
K
dry
-
hiP
1
K
0
Step 5: Calculate the bulk modulus of the saturated rock (K
r
) from
K
r
¼
K
m
1 þ a
m
dP=d
where
a
m
¼ 1
K
m
K
ms
Step 6: Calculate the shear modulus of the modified frame (m
m
) from
1
m
dry
1
m
m
¼
4
15
1
K
dry
1
K
md
where
1
K
md
¼
1
~
K
ms
þ
1
K
dry
-
hiP
1
K
0
~
K
ms
¼K
msd
þ aK
0
½1 f ðxÞ
Step 7: Finally, calculate velocities V
P
and V
S
and inverse quality factors Q
1
P
and
Q
1
S
from
V
P
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
ReðK
r
þ
4
3
m
m
Þ
s
; V
S
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
Reðm
m
Þ
s
Q
1
P
¼
ImðK
r
þ
4
3
m
m
Þ
ReðK
r
þ
4
3
m
m
Þ
; Q
1
S
¼
Imðm
m
Þ
Reðm
m
Þ
Step 8: The velocities and inverse quality factors have been found for an assumed Z
value (Figure 6.11.1). To find the true Z value, one has to change it until the
theoretical value of one of the four parameters (V
P
, V
S
, Q
P
–1
,orQ
S
–1
) matches the
experimentally measured value at a given frequency. It is preferred that V
P
be used
for this purpose. The Z value thus obtained should be used for calculating the
velocities and quality factors at varying frequencies. The Z value can also be used
for a different pore fluid. In the latter case, use the following value for Z :
Z
new
¼ Z
ffiffiffiffiffiffiffiffiffi
new
r
where the subscript new indicates the new pore fluid.
300 Fluid effects on wave propagation
The notation used is: K
dry
is the effective bulk modulus of dry rock, K
dry-hiP
is the
effective bulk modulus of dry rock at very high pressure, K
0
is the bulk modulus of
the mineral material making up the rock, K
fl
is the effective bulk modulus of the pore
fluid, is the viscosity of the pore fluid, f is porosity, m
dry
is the effective shear
modulus of dry rock, r is rock density, and o is angular frequency.
Uses
The extension of the Mavko–Jizba squirt relations can be used to calculate saturated-
rock velocities and attenuation at any frequency.
Assumptions and limitations
The following assumptions underlie the extension of the Mavko–Jizba squirt relations:
the rock is isotropic;
all minerals making up the rock have the same bulk and shear moduli; and
fluid-bearing rock is completely saturated.
Extensions
Additional extensions of the Mavko–Jizba squirt relations include the following:
for mixed mineralogy, one can usually use an effective average modulus for K
0
;
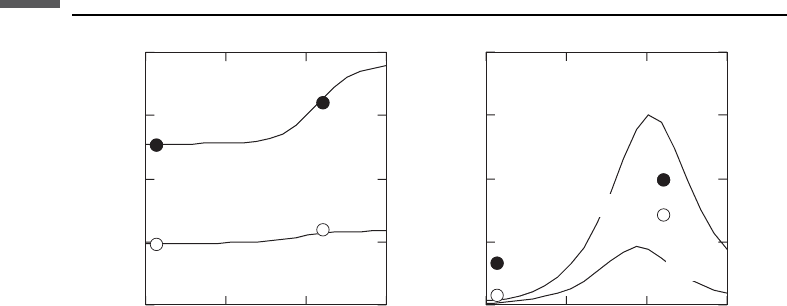
Murphy et al. (1984) introduced a micromechanical model to describe the squirt-
flow mechanism. They considered a composite grain-contact stiffness, which is the
parallel combination of the solid–solid contact stiffness and the stiffness of a fluid-
filled gap, shown in Figure 6.11.2.
2000
1000
3000
4000
5000
3.5 4.5 5.5 6.5
V
P
V
S
V
P
and V
S
(m/s)
Log frequency (Hz)
0.1
0.2
0.3
0.4
3.5 4.5 5.5 6.5
Q
P
−1
Inverse quality factors
Log frequency (Hz)
Q
S
−1
0
Figure 6.11.1 The V
S
and inverse quality factors have been predicted by determining Z from V
P
measurements (0.18 porosity limestone). Closed symbols are for P-waves; open symbols are for
S-waves.
301 6.11 Extension of Mavko–Jizba squirt relations for all frequencies
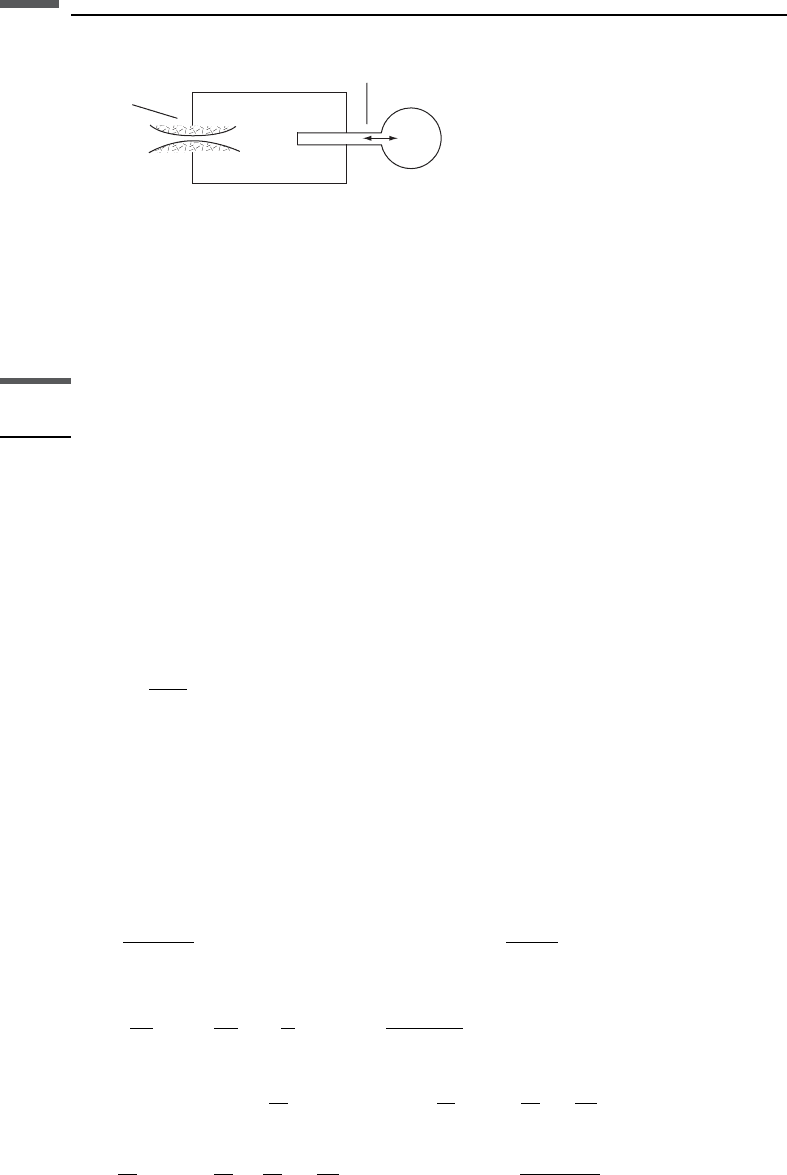
When modeling the solid–solid contact, surface energy is taken into account. The
hydrodynamic contact model takes into account the squirt flow of pore fluid between
a thin crack and a stiff, large pore. The results qualitatively match the observed
velocity dispersion and attenuation in sandstones.
6.12 Biot–squirt model
Synopsis
Dvorkin and Nur (1993) and Dvorkin et al. (1994) introduced a unified Biot–squirt
(BISQ) model. The model is applicable to rocks at high pressure with compliant
cracks closed. The rock is partially saturated or apparently fully saturated (meaning
that there are small, undetectable amounts of free gas left in pores). The zero-
frequency velocity limit, as given by BISQ, is
V
P0
¼
ffiffiffiffiffiffiffiffiffi
M
dry
s
The M
dry
term is the dry-rock uniaxial-strain modulus ðM
dry
¼
dry
V
2
P
-
dry
Þ, r is rock
density (at saturation), and V
P-dry
and r
dry
are the dry-rock P-wave velocity and
density, respectively. The BISQ high-frequency velocity limit is the same as in the
Biot theory.
BISQ gives the following expressions for P-wave velocity (V
P
), the attenuation
coefficient (a
P
), and the inverse quality factor ðQ
1
P
Þ at apparently full saturation:
V
P
¼
1
Re
ffiffiffi
Y
p
; a
P
¼ o Im
ffiffiffi
Y
p
; Q
1
P
¼
2a
P
V
P
o
Y ¼
B
2A
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
B
2A
2
C
A
s
; A ¼
F
sq
M
dry
2
2
B ¼ F
sq
2g
1
2
M
dry
þ F
sq
g
2
1 þ
a
2
þ i
o
c
o
2
C ¼
1
2
þ 1 þ
1
2
a
2
þ i
o
c
o
; F
sq
¼ F 1
2J
1
ðlRÞ
lRJ
0
ðlRÞ
Dry solid–solid
contact
Fluid-filled gap
with squirt flow
Figure 6.11.2 Schematic of a micromechanical model to describe the squirt-flow mechanism.
302 Fluid effects on wave propagation

l
2
¼
fl
o
2
F
þ
a
=
fl
þ i
o
c
o
;
1
¼ð1 Þ
s
;
2
¼
fl
o
c
¼
k
fl
; g ¼ 1
K
dry
K
0
;
1
F
¼
1
K
fl
þ
1
K
0
1
K
dry
K
0
where R is the characteristic squirt-flow length, f is porosity, r
s
and r
fl
are the
solid-phase and fluid-phase densities, respectively; r
a
¼(1 – a)fr
fl
is the Biot
inertial-coupling density; is the pore-fluid viscosity; k is rock permeability; K
dry
is the dry-rock bulk modulus; K
0
and K
fl
are the solid-phase and the fluid-phase bulk
moduli, respectively; o is the angular frequency; and J
0
and J
1
are Bessel functions of
zero and first order, respectively. The tortuosity a (sometimes called the structure
factor) is a purely geometrical factor independent of the solid or fluid densities and is
always greater than 1 (see Section 6.1).
All input parameters, except for the characteristic squirt-flow length, are experi-
mentally measurable. The latter has to be either guessed (it should have the same
order of magnitude as the average grain size or the average crack length) or adjusted by
using an experimental measurement of velocity versus frequency (see Section 6.11).
For partially saturated rock at saturation S,
R
s
¼ R
ffiffiffi
S
p
has to be used instead of R in the preceding formulas. To avoid numerical problems
(caused by resonance) at high frequencies,
l
2
¼ i
fl
oo
c
F
can be used instead of
l
2
¼
fl
o
2
F
þ
a
=
fl
þ i
o
c
o
At lower frequencies, o
c
=o 1, the following simplified formulas can be used:
Y ¼
ð1 Þ
s
þ
fl
M
dry
þ F
sq
g
2
=
; F
sq
¼ F 1
2J
1
ðxÞ
xJ
0
ðxÞ
x ¼
ffiffiffiffiffiffiffiffiffiffiffi
i
R
2
o
k
r
; k ¼
kF
The BISQ formulas give the Biot theory expressions for the velocity and attenuation
if F
sq
¼F .
Uses
The BISQ formulas can be used to calculate partially saturated rock velocities and
attenuation (at high pressure) at any frequency.
303 6.12 Biot–squirt model
Assumptions and limitations
The BISQ formulas are based on the following assumptions:
the rock is isotropic;
all minerals making up the rock have the same bulk and shear moduli.
In the low-frequency limit, the BISQ formulas are not consistent with the Gassmann
predictions.
Extensions
For mixed mineralogy, one can usually use an effective average modulus for K
0
.
6.13 Chapman et al. squirt model
Synopsis
Chapman et al. (2002) presented a squirt or local flow model that considers
frequency-dependent, wave-induced exchange of fluids between pores and cracks,
as well as between cracks of different orientations. The cracks are idealized as oblate
spheroids with small aspect ratio r, uniform crack radius a, and crack density e. The
pores are considered to be spherical. The bulk and shear moduli and Lame
´
parameter
of the solid mineral matrix (rock without cracks or pores) are denoted by K, m, and l,
respectively, while the fluid bulk modulus is K
f
. The total porosity is f.
The frequency-dependent effective bulk and shear moduli, K
eff
and m
eff
, are expressed
as follows (Chapman et al., 2006):
K
eff
¼K e
43l þ 2mðÞl þ 2mðÞ
mlþ mðÞ
1 3A oðÞ½4prA oðÞ
3l þ 2m
4m
l þ 2m
3l þ 2m
þ B oðÞ
3B oðÞ
and
m
eff
¼m
16
45
e
1
1 þ K
c
mlþ 2mðÞ
3l þ 4m
K
c
þ
1
1 þ i ot
32
45
e
mlþ 2mðÞ
3l þ 4m
15mlþ 2mðÞ
9l þ 14m
where o is the angular frequency, and the other parameters are
A oðÞ¼
1 þ i ogtðÞ
lþ2m
lþm
16e
27 1þK
p
ðÞ
þ
lþm
3lþ2m
þ iot
1
31þK
c
ðÞ
g
0
hi
1 þ i ot þ 1 þ iogtðÞ
16e 1þK
c
ðÞ
9 1þK
p
ðÞ
lþ2m
lþm
304 Fluid effects on wave propagation
B oðÞ¼
1
31þK
c
ðÞ
þ
91þK
p
ðÞ
16 1þK
c
ðÞ
lþmðÞ
3lþ2mðÞ
þ
iot
1þiot
g
0
1
31þK
c
ðÞ
hi
91þK
p
ðÞ
lþmðÞ
16 1þK
c
ðÞlþ2mðÞ
þ
1þiogt
1þiot
g
0
¼ g
l þ 2m
3l þ 2mðÞ1 þ K
p
g ¼
3plþ mðÞ1 þ K
p
4 l þ 2mðÞ1 þ K
c
ðÞ
K
p
¼
4m
3K
f
and
K
c
¼
pmr l þ mðÞ
K
f
l þ 2mðÞ
The timescale parameter t controls the frequency regime over which the dispersion
occurs. It is proportional to the fluid viscosity and inversely proportional to the
permeability k, and depends on the crack radius a. For small aspect ratios (r < 10
3
),
t is approximately given by
t
4a
3
1 nðÞ
9k&m
where z is a characteristic grain size, and n is the Poisson ratio of the solid mineral.
One of the requirements for any model of fluid-related dispersion is that in the low-
frequency limit the predictions should be consistent with the Gassmann equations.
The Chapman et al. (2002) formulas are consistent with the Gassmann predictions in
the low-frequency limit, whereas the BISQ model (Dvorkin and Nur, 1993) and the
equant porosity model (Hudson et al., 1996) are not.
Uses
The formulas can be used to calculate squirt-related velocity dispersion and attenu-
ation at any frequency.
Assumptions and limitations
The formulas assume idealized spherical pores and penny-shaped crack geometry,
with all cracks having the same radius:
the rock is isotropic;
all minerals making up the rock have the same bulk and shear moduli.
Extensions
The formulation has been extended to meso-scale aligned fractures with coupled
fluid motion at two scales (Chapman, 2003).
305 6.13 Chapman et al. squirt model

6.14 Anisotropic squirt
Synopsis
The squirt or local flow model suggests that the fluctuating stresses in a rock caused
by a passing seismic wave induce pore-pressure gradients at virtually all scales of
pore-space heterogeneity – particularly on the scale of individual grains and pores.
These gradients impact the viscoelastic behavior of the rock; at high frequencies,
when the gradients are unrelaxed, all elastic moduli will be stiffer than at low
frequencies, when the gradients are relaxed. (The latter case is modeled by the
anisotropic Gassmann and Brown and Korringa (1975) formalisms.) Mukerji and
Mavko (1994) derived simple theoretical formulas for predicting the very high-
frequency compliances of saturated anisotropic rocks in terms of the pressure depend-
ence of dry rocks. The prediction is made in two steps: first, the squirt effect is
incorporated as high-frequency “wet-frame compliances” S
ðwetÞ
ijkl
; which are derived
from the dry compliances S
ðdryÞ
ijkl
: Then these wet-frame compliances are substituted
into the Gassmann (Section 6.3), Brown and Korringa (see Section 6.4) or Biot
relations (see Section 6.1) (in place of the dry compliances) to incorporate the
remaining fluid saturation effects. For most crustal rocks, the amount of squirt
dispersion is comparable to or greater than Biot’s dispersion, and thus using Biot’s
theory alone will lead to poor predictions of high-frequency saturated velocities.
Exceptions include very high permeability materials such as ocean sediments and
glass beads, rocks at very high effective pressure, when most of the soft, crack-like
porosity is closed, and rocks near free boundaries such as borehole walls.
The wet-frame compliance is given by (repeated indices imply summation)
S
ðwetÞ
ijkl
S
ðdryÞ
ijkl
S
ðdryÞ
aabb
1 þ
soft
ðb
f
b
0
Þ=S
ðdryÞ
ggdd
G
ijkl
where S
ðdryÞ
ijkl
¼ S
ðdryÞ
ijkl
S
ðdry high PÞ
ijkl
is the change in dry compliance between the
pressure of interest and very high confining pressure, f
soft
is the soft porosity that
closes under high confining pressure, and b
f
and b
0
are the fluid and mineral
compressibilities, respectively. The soft porosity is often small enough that the
second term in the denominator can be ignored. The tensor G
ijkl
represents the
fraction of the total compliance that is caused by volumetric deformation of crack-
like pore space with different orientations for a given externally applied load. The
tensor depends on the symmetry of the crack distribution function and is expressed as
an integral over all orientations:
G
ijkl
¼
Z
f ðÞn
i
n
j
n
k
n
l
d
where f(O) is the crack-orientation distribution function normalized so that its integral
over all angles equals unity, and n
i
is the unit normal to the crack faces. Elements of
306 Fluid effects on wave propagation
