Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook
Подождите немного. Документ загружается.


patch at scales smaller than L
c
, but neighboring patches at scales >L
c
will not be
equilibrated with each other. Fluid flow resulting from unequilibrated pore pressures
between patches of different fluids will cause attenuation and dispersion of seismic
waves traveling through the rock. White (1975) modeled the seismic effects of patchy
saturation by considering porous rocks saturated with brine but containing spherical
gas-filled regions. Dutta and Ode
´
(1979) gave a more rigorous solution for White’s
model by using Biot’s equations for poroelasticity. The patches (spheres) of hetero-
geneous saturation are much larger than the grain scale but are much smaller than
the wavelength. The idealized geometry of a unit cell consists of a gas-filled sphere
of radius a placed at the center of a brine-saturated spherical shell of outer radius b
(b > a). Adjacent unit cells do not interact with each other. The gas saturation is
S
g
¼a
3
/b
3
. The inner region will be denoted by subscript 1 and the outer shell by
subscript 2. In the more rigorous Dutta and Ode
´
formulation, the dry-frame properties
(denoted by subscript “dry” in the following equations) in the two regions may be
different. However, in White’s approximate formulation, the dry-frame properties are
assumed to be the same in regions 1 and 2. White’s equations as given below
(incorporating a correction pointed out by Dutta and Seriff, 1979) yield results that
agree very well with the Dutta–Ode
´
results. The complex bulk modulus, K
*
, for the
partially saturated porous rock as a function of angular frequency o is given by
K
¼
K
1
1 K
1
W
¼ K
r
þ iK
i
where
W ¼
3a
2
ðR
1
R
2
ÞðQ
1
þ Q
2
Þ
b
3
ioðZ
1
þ Z
2
Þ
R
1
¼
K
1
K
dry
1
1 K
dry
1
=K
0
1
3K
2
þ 4m
2
K
2
ð3K
1
þ 4m
2
Þþ4m
2
ðK
1
K
2
ÞS
g
R
2
¼
K
2
K
dry
2
1 K
dry
2
=K
0
2
3K
1
þ 4m
1
K
2
ð3K
1
þ 4m
2
Þþ4m
2
ðK
1
K
2
ÞS
g
Z
1
¼
1
a
k
1
1 e
2a
1
a
ða
1
a 1Þþða
1
a þ 1Þe
2a
1
a
Z
2
¼
2
a
k
2
ða
2
b þ 1Þþða
2
b 1Þe
2a
2
ðbaÞ
ða
2
b þ 1Þða
2
a 1Þða
2
b 1Þða
2
a þ 1Þe
2a
2
ðbaÞ
a
j
¼ðio
j
=k
j
K
Ej
Þ
1=2
K
Ej
¼ 1
K
fj
ð1 K
j
=K
0j
Þð1 K
dryj
=K
0j
Þ
K
j
ð1 K
fj
=K
0j
Þ
K
Aj
327 6.18 Partial saturation: White and Dutta–Ode
´
model

K
Aj
¼
K
fj
þ
1
K
0j
K
dryj
K
2
0j
!
1
Q
j
¼
ð1 K
dryj
=K
0j
ÞK
Aj
K
j
Here, j ¼1 or 2 denotes quantities corresponding to the two different regions; and
K
f
are the fluid viscosity and bulk modulus, respectively; f is the porosity; k is the
permeability; and K
0
is the bulk modulus of the solid mineral grains. The saturated
bulk and shear moduli, K
j
and m
j
, respectively, of region j are obtained from
Gassmann’s equation using K
dry j
, m
dry j
, and K
f j
. When the dry-frame moduli are
the same in both regions, m
1
¼m
2
¼m
dry
because Gassmann predicts no change in the
shear modulus upon fluid substitution. At the high-frequency limit, when there is no
fluid flow across the fluid interface between regions 1 and 2, the bulk modulus is
given by
K
1
ðno
-
flowÞ¼
K
2
ð3K
1
þ 4m
2
Þþ4m
2
ðK
1
K
2
ÞS
g
ð3K
1
þ 4m
2
Þ3ðK
1
K
2
ÞS
g
This assumes that the dry-frame properties are the same in the two regions. The low-
frequency limiting bulk modulus is given by Gassmann’s relation with an effective
fluid modulus equal to the Reuss average of the fluid moduli. In this limit the fluid
pressure is constant and uniform throughout the medium:
Kðlow-frequencyÞ¼
K
2
ðK
1
K
dry
ÞþS
g
K
dry
ðK
2
K
1
Þ
ðK
1
K
dry
ÞþS
g
ðK
2
K
1
Þ
Note that in White (1975) the expressions for K
E
and Q had the P-wave modulus
M
j
¼K
j
þ 4m
j
/3 in the denominator instead of K
j
. As pointed out by Dutta and Seriff
(1979), this form does not give the right low-frequency limit. An estimate of the
transition frequency separating the relaxed and unrelaxed (no-flow) states is given by
f
c
k
2
K
E2
p
2
b
2
which has the length-squared dependence characteristic of diffusive phenomena.
When the central sphere is saturated with a very compressible gas (caution: this
may not hold at reservoir pressures) R
1
, Q
1
, Z
1
0. The expression for the effective
complex bulk modulus then reduces to
K
¼
K
1
1 þ 3a
2
R
2
Q
2
K
1
=ðb
3
ioZ
2
Þ
Dutta and Ode
´
obtained more rigorous solutions for the same spherical geometry
by solving a boundary-value problem involving Biot’s poroelastic field equations.
They considered steady-state, time-harmonic solutions for u and w, the displacement
328 Fluid effects on wave propagation
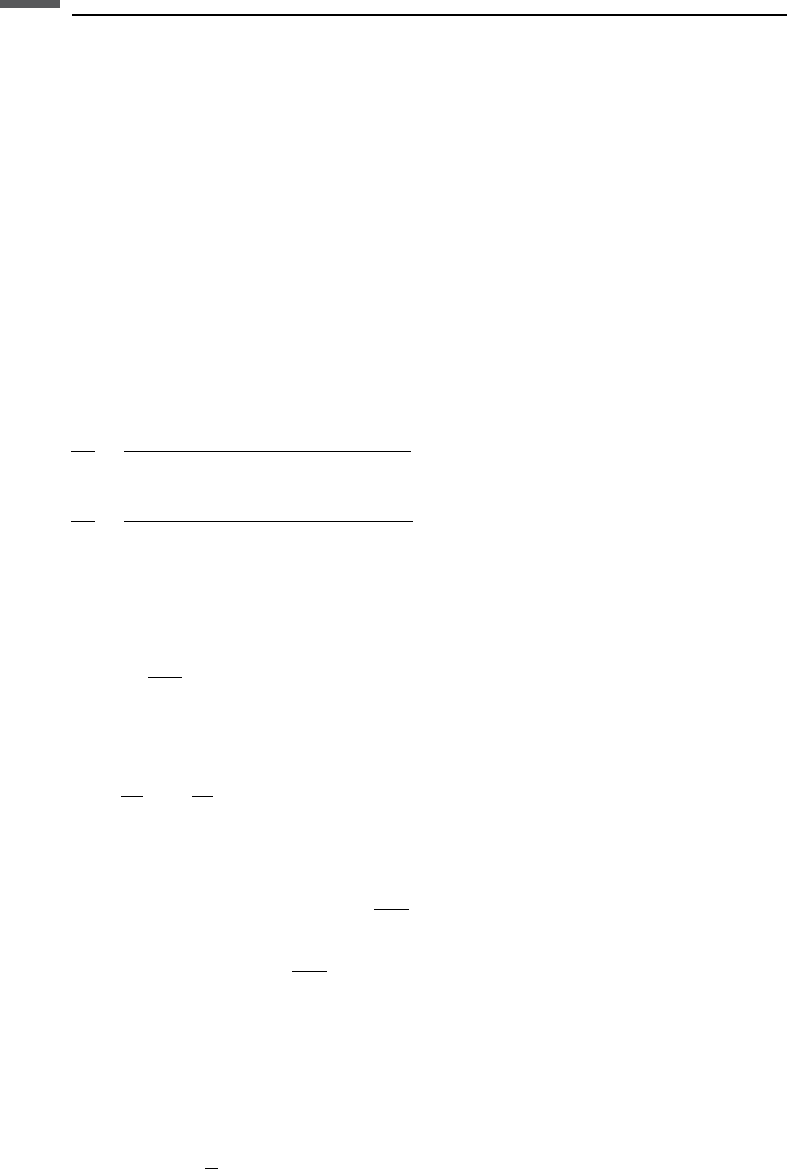
of the porous frame and the displacement of the pore fluid relative to the frame,
respectively. The solutions in the two regions are given in terms of spherical Bessel
and Neumann functions, j
1
and n
1
, of order 1. The general solution for w in region 1
for purely radial motion is
wðrÞ¼w
c
ðrÞþw
d
ðrÞ
w
c
ðrÞ¼C
1
j
1
ðk
c
rÞþC
2
n
1
ðk
c
rÞ
w
d
ðrÞ¼C
3
j
1
ðk
d
rÞþC
4
n
1
ðk
d
rÞ
where C
1
, C
2
, C
3
, and C
4
are integration constants to be determined from the
boundary conditions at r ¼0, r ¼a, and r ¼b. A similar solution holds for region 2,
but with integration constants C
5
, C
6
, C
7
, and C
8
. The wavenumbers k
c
and k
d
in each
region are given in terms of the moduli and density corresponding to that region:
k
2
c
o
2
¼
f
ðM
c
þ 2gDÞð2gD
c
þ 2DÞ
ð4g
2
D
2
2DMÞ
k
2
d
o
2
¼
f
ðM
d
þ 2gDÞð2gD
d
þ 2DÞ
ð4g
2
D
2
2DMÞ
where
¼ð1 Þ
0
þ
f
g ¼ 1
K
dry
K
0
M ¼ K þ
4
/
3
m
D ¼
K
0
2
g þ
K
f
ðK
0
K
f
Þ
1
and s
c
and s
d
are the two complex roots of the quadratic equation
ð
f
M 2gDÞ
2
þ Mm 2D
iM
ko
þ 2mgD 2
f
D 2i
gD
ko
¼ 0
where m ¼sr
f
/f. The tortuosity parameter s (sometimes called the structure factor) is
a purely geometrical factor independent of the solid or fluid densities and is never less
than 1 (see Section 6.1 on Biot theory). For idealized geometries and uniform flow,
s usually lies between 1 and 5. Berryman (1981) obtained the relation
s ¼ 1 x 1
1
329 6.18 Partial saturation: White and Dutta–Ode
´
model
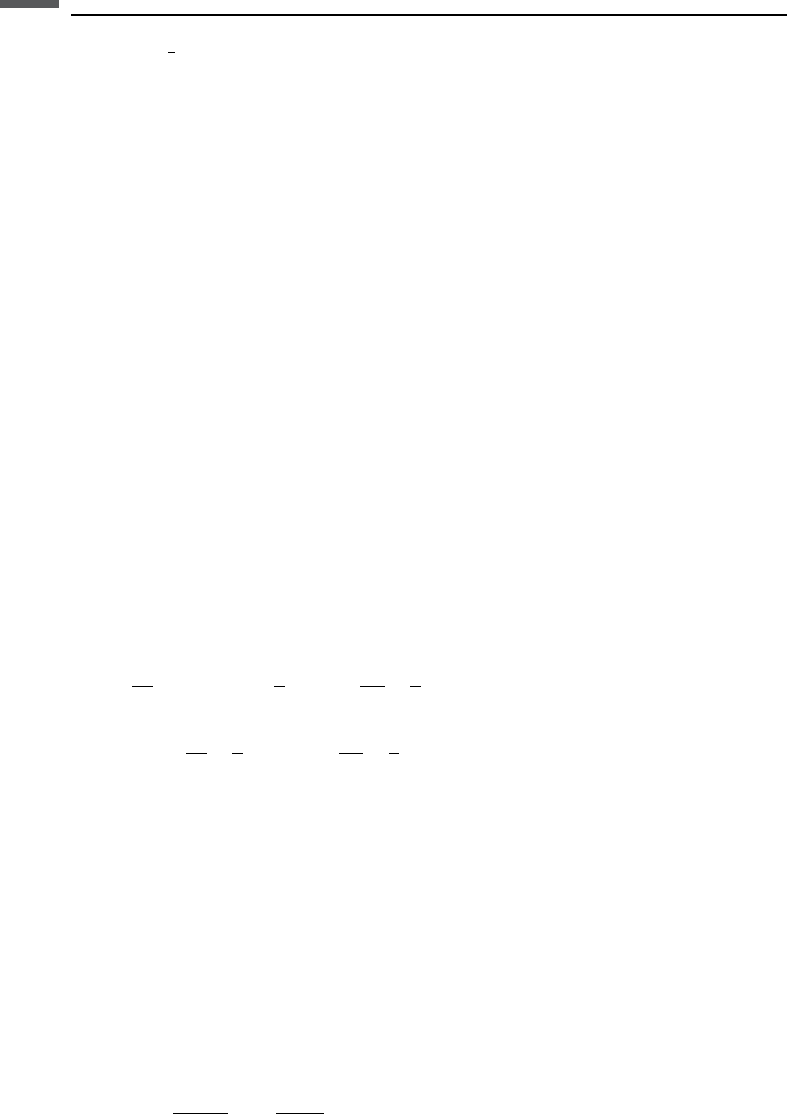
where x ¼
1
2
for spheres and lies between 0 and 1 for other ellipsoids. For uniform
cylindrical pores with axes parallel to the pore pressure gradient, s equals 1 (the
minimum possible value), whereas for a random system of pores with all possible
orientations, s ¼3 (Stoll, 1977). The solutions for u are given as
uðrÞ¼u
c
ðrÞþu
d
ðrÞ
u
c
ðrÞ¼
d
w
c
ðrÞ; u
d
ðrÞ¼
c
w
d
ðrÞ
The integration constants are obtained from the following boundary conditions:
(1) r ! 0, w
1
(r) ! 0
(2) r ! 0, u
1
(r) ! 0
(3) r ¼a, u
1
(r) ¼u
2
(r)
(4) r ¼a, w
1
(r) ¼w
2
(r)
(5) r ¼a, t
1
(r) ¼t
2
(r)
(6) r ¼a, p
1
(r) ¼p
2
(r)
(7) r ¼b, t
2
(r) ¼–t
0
(8) r ¼b, w
2
(r) ¼0
The first two conditions imply no displacements at the center of the sphere because
of purely radial flow and finite fluid pressure at the origin. These require C
2
¼C
4
¼0.
Conditions (3)–(6) come from continuity of displacements and stresses at the inter-
face. The bulk radial stress is denoted by t, and p denotes the fluid pressure. These
parameters are obtained from u and w by
t ¼M
]u
]r
þ 2ðM 2mÞ
u
r
þ 2gD
]w
]r
þ
2
r
w
p ¼2gD
]u
]r
þ
2
r
u
2D
]w
]r
þ
2
r
w
Condition (7) gives the amplitude t
0
of the applied stress at the outer boundary, and
condition (8) implies that the outer boundary is jacketed. These boundary conditions
are not unique and could be replaced by others that may be appropriate for the
situation under consideration. The jacketed outer boundary is consistent with non-
interacting unit cells. The remaining six integration constants are obtained by solving
the linear system of equations given by the boundary conditions. Solving the linear
system requires considerable care (Dutta and Ode
´
, 1979). The equations may become
ill-conditioned because of the wide range of the arguments of the spherical Bessel and
Neumann functions. Once the complete solution for u (r) is obtained, the effective
complex bulk modulus for the partially saturated medium is given by
K
ðoÞ¼
t
0
V=V
¼
t
0
b
3uðbÞ
The P-wave velocity V
P
and attenuation coefficient a
P
are given in terms of the
complex P-wave modulus M
*
and the effective density r
*
330 Fluid effects on wave propagation
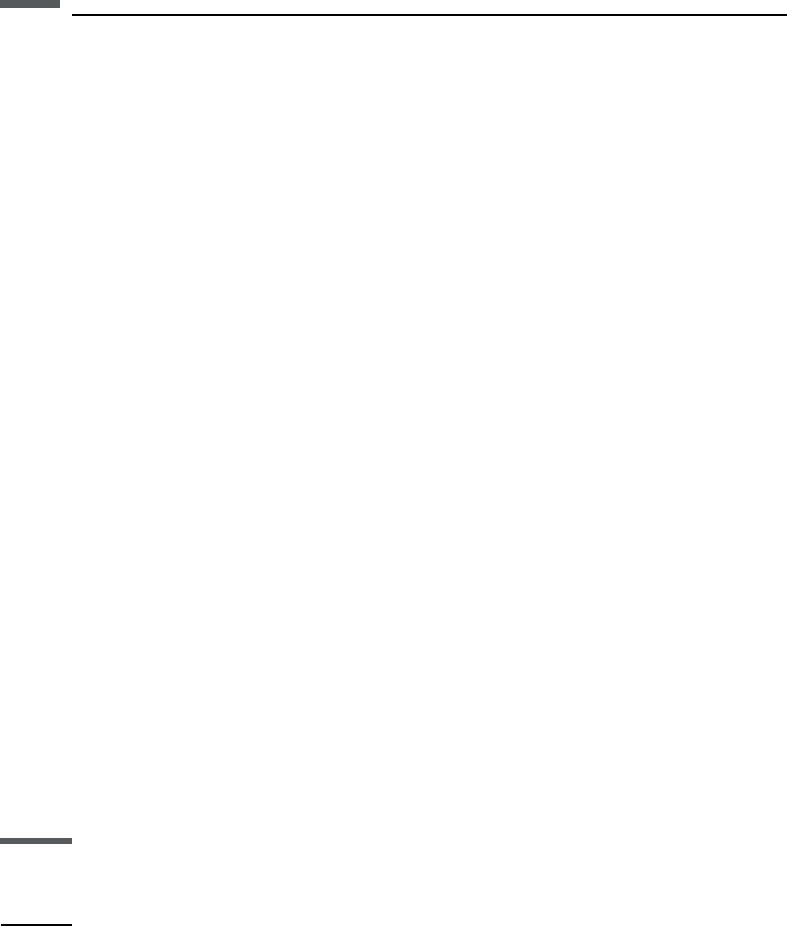
¼ S
g
½ð1 Þ
0
þ
f1
þð1 S
g
Þ½ð1 Þ
0
þ
f2
M
¼ M
r
þ iM
i
¼ K
r
þ 4m
=3 þ iK
i
m
¼ m
1
¼ m
2
¼ m
dry
V
P
¼ðjM
j=
Þ
1=2
= cosðy
P
=2Þ
a
P
¼ o tanðy
P
=2Þ=V
P
y
P
¼ tan
1
ðM
i
=M
r
Þ
Uses
The White and Dutta–Ode
´
models can be used to calculate velocity dispersion and
attenuation in porous media with patchy partial saturation.
Assumptions and limitations
The White and Dutta–Ode
´
models are based on the following assumptions:
the rock is isotropic;
all minerals making up the rock are isotropic and linearly elastic;
the patchy saturation has an idealized geometry consisting of a sphere saturated
with one fluid within a spherical shell saturated with another fluid;
the porosity in each saturated region is uniform, and the pore structure is smaller
than the size of the spheres; and
the patches (spheres) of heterogeneous saturation are much larger than the grain
scale but are much smaller than the wavelength.
6.19 Velocity dispersion, attenuation, and dynamic permeability
in heterogeneous poroelastic media
Synopsis
Wave-induced fluid flow in heterogeneous porous media can cause velocity disper-
sion and attenuation. The scale of the heterogeneities is considered to be much larger
than the pore scale but much smaller than the wavelength of the seismic wave. An
example would be heterogeneities caused by patchy saturation discussed in Section 6.17.
Muller and Gurevich (2005a, 2005b, 2006) applied the method of statistical
smoothing for Biot’s poroelastici ty equations in a random, heterogeneous, porous
medium and derived the effective wavenumbers for the fast and slow P-waves.
The parameters of the poroelastic random medium consist of a smooth background
331 6.19 Heterogeneous poroelastic media

component and a zero-mean fluctuating component. The statistical properties of the
relative fluctuations of any two parameters X and Y are described by variances and
covariances denoted by
2
XX
and
2
XY
, respectively. The spatial distribution of the
random heterogeneities is described by a normalized spatial correlation function
BðrÞ. In the following equations, all poroelastic parameters are assumed to have the
same normalized spatial correlation function and correlation length, though the
general results of Muller and Gurevich (2005a) allow for different correlation lengths
associated with each random property.
The effective P-wavenumber
k
P
in three-dimensional random poroelastic media
with small fluctuations can be written as (Muller and Gurevich, 2005b)
k
P
¼ k
P
1 þ
2
þ
1
k
2
Ps
Z
1
0
rBðrÞexpðirk
Ps
Þdr
where k
P
is the wavenumber in the homogeneous background and the dimensionless
coefficients D
1
and D
2
are given by
1
¼
a
2
M
2P
d
2
HH
2
2
HC
þ
2
CC
þ
32
15
G
2
H
2
2
GG
8
3
G
H
2
HG
þ
8
3
G
H
2
GC
2
¼
1
þ
1
2
2
HH
4
3
G
H
2
HG
þ
4G
H
þ 1
4
15
G
H
2
GG
and the other parameters are: k
Ps
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
io=ðk
0
NÞ
p
is the wavenumber of the Biot slow
wave in the homogeneous background, o is the angular frequency, is the fluid
viscosity, k
0
is the background permeability, G is the background shear modulus,
P
d
is the dry (drained) P-wave modulus of the background, H is the saturated P-wave
modulus of the background, related to P
d
by Gassmann’s equation as H ¼ P
d
þ a
2
M,
M ¼ða Þ=K
0
þ =K
f
½
1
, f is the background porosity, a ¼ 1 K
d
=K
0
is the
Biot–Willis coefficient, K
d
is the dry bulk modulus, K
0
is the mineral (solid-phase)
bulk modulus, K
f
is the fluid bulk modulus, N ¼ MP
d
=H, and C ¼aM.
Expressions for velocity dispersion V(o) and attenuation or inverse quality factor
Q
1
are obtained from the real and imaginary parts of the effective wavenumber:
VðoÞ¼
o
Re
k
P
¼ V
0
1
2
þ 2
1
k
2
Psr
Z
1
0
rBðrÞexpðrk
Psr
Þsinðrk
Psr
Þdr
V
0
¼
ffiffiffiffiffiffiffiffiffi
H=
p
¼constant background P-wave velocity in the saturated porous medium
and r is the saturated bulk density.
k
Psr
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
o=ð2k
0
NÞ
p
¼real part of the slow P-wavenumber k
Ps
.
For low-loss media, Q
1
can be written as
Q
1
ðoÞ¼
2Im
k
P
Re
k
P
¼ 4
1
k
2
Psr
Z
1
0
rBðrÞexpðrk
Psr
Þcosðrk
Psr
Þdr
332 Fluid effects on wave propagation
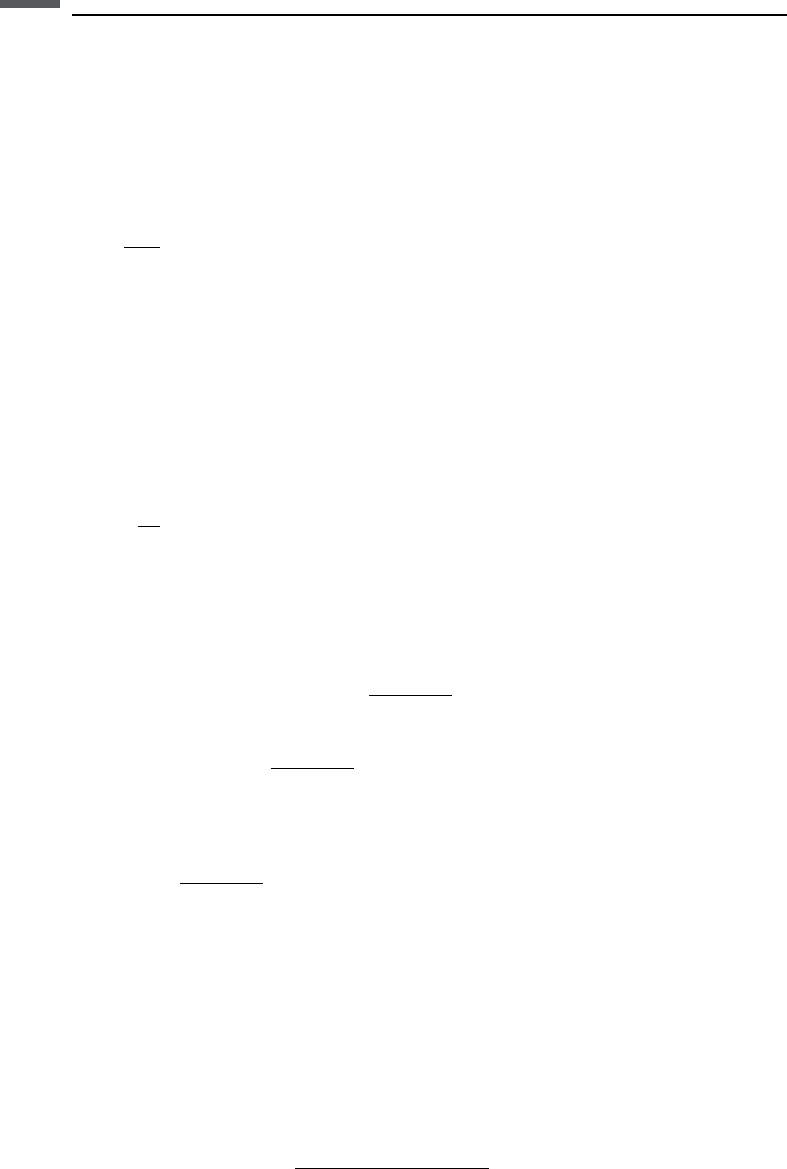
The term D
1
is a measure of the magnitude of attenuation and frequency-dependent
velocity dispersion, while D
2
produces a frequency-independent velocity shift.
The validity of the approximations for the effective P-wavenumber are expressed
mathematically as
max
1
jk
Ps
jaðÞ
2
;
2
no
1
a
2
k
0
N
o
B
where a is the correlation length and o
B
¼ =ðk
0
f
Þ is the Biot characteristic
frequency with r
f
being the fluid density. These conditions arise from the weak-
contrast assumption and the low-frequency approximation necessary for the derivation
(Muller and Gurevich, 2005b).
The spatial correlation function B(r) and the power spectrum of the fluctuations
F(k) are related by a Fourier transform. If the medium is statistically isotropic the
relation can be expressed as a three-dimensional Hankel transform:
BðrÞ¼
4p
r
Z
1
0
kðkÞsinðkrÞdk
where k is the spatial wavenumber of the fluctuations. In terms of the power
spectrum, the expressions for velocity and inverse quality factor are (Muller and
Gurevich, 2005b):
VðoÞ¼V
0
1
2
þ 16p
1
Z
1
0
k
4
Psr
k
2
4k
4
Psr
þ k
4
ðkÞdk
Q
1
ðoÞ¼16p
1
Z
1
0
k
2
Psr
k
4
4k
4
Psr
þ k
4
ðkÞdk
The factor
ðk; k
Psr
Þ¼
k
2
Psr
k
4
4k
4
Psr
þ k
4
acts as a filter and controls which part of the fluctuation spectrum gives contributions
to the velocity dispersion and attenuation.
Results for specific correlation functions
Muller and Gurevich (2005b) give explicit analytic results for specific correlation
functions. For an exponential correlation function BðrÞ¼exp jrj=a½and
VðoÞ¼V
0
1
2
þ
1
4ðak
Psr
Þ
3
ð1 þ k
Psr
aÞ
1 þ 2k
Psr
a þ 2k
2
Psr
a
2
ðÞ
2
"#
333 6.19 Heterogeneous poroelastic media

Q
1
ðoÞ¼
1
4ðak
Psr
Þ
2
ð1 þ 2k
Psr
aÞ
1 þ 2k
Psr
a þ 2k
2
Psr
a
2
ðÞ
2
For a Gaussian correlation function BðrÞ¼expðr
2
=a
2
Þ, and Muller and Gurevich
obtain
VðoÞ¼V
0
1
2
þ
1
ðak
Psr
Þ
2
ffiffiffi
p
p
4
X
z¼z
þ
z¼z
ak
Psr
z
exp½ðak
Psr
zÞ
2
=4erfc½ak
Psr
z=2
()
Q
1
ðoÞ¼2
1
ðak
Psr
Þ
2
1
ffiffiffi
p
p
4
X
z¼z
þ
z¼z
ak
Psr
z exp½ðak
Psr
zÞ
2
=4erfc½ak
Psr
z=2
()
where z
þ
¼ 1 þ i, z
¼ 1 i, and z
denotes the complex conjugate.
The von Karman correlation function with two parameters, the correlation length a,
and the Hurst coefficient n (0 < n 1), is expressed as
BðrÞ¼2
1n
1
ðnÞ
r
a
n
K
n
ðr=aÞ
where G is the Gamma function and K
n
is the modified Bessel function of the third
kind. When n ¼
1
2
, the von Karman function becomes identical to the exponential
correlation function. The equivalent spectral representation for general n is
ðkÞ¼
a
3
ðn þ
3
2
Þ
p
3=2
ðnÞð1 þ k
2
a
2
Þ
nþ3=2
Using the spectral representation, Muller and Gurevich ( 2005b) derive expressions
for fast P-wave velocity dispersion and inverse quality factor as described below:
VðoÞ¼V
0
1
2
1
2
c
1
1
1
þ
2
þ
3
ðÞ
Q
1
ðoÞ¼c
1
1
1
þ
2
þ
3
½
with
1
¼4c
2
ð1 þ nÞðak
Psr
Þ
2
3
F
2
1; 1 þ
n
2
;
3
2
þ
n
2
;
3
4
;
5
4
; 4ðak
Psr
Þ
4
2
¼
1
2
n þ
1
2
ð2n þ 3Þc
3
B
3=4n=2
cos
3
4
þ
n
2
A
3
¼ n þ
3
2
3
2
þ n
B
5=4n=2
2ðak
Psr
Þ
2
cosðc
3
AÞþsinðc
3
AÞ
hi
1
¼ c
23
F
2
1;
1
2
þ
n
2
; 1 þ
n
2
;
1
4
;
3
4
; 4ðak
Psr
Þ
4
334 Fluid effects on wave propagation

2
¼
1
2
n þ
3
2
ð2n þ 3ÞB
3=4n=2
cos
3
4
þ
n
2
A
3
¼ n þ
5
2
B
5=4n=2
2ðak
Psr
Þ
2
cosðc
3
AÞþsinðc
3
AÞ
hi
c
1
¼
16
ffiffiffi
p
p
ðak
Psr
Þ
3
ðnÞð2n þ3Þ
c
2
¼
ðn þ 1Þð2n þ 3Þ
2
ffiffiffi
p
p
ak
Psr
c
3
¼
1
4
þ
n
2
A ¼ 2 arctan 2ðak
Psr
Þ
2
hi
B ¼ 1 þ 4ðak
Psr
Þ
4
p
F
q
ðx
1
; ...; x
p
; &
1
; ...;&
q
; xÞ¼generalized hypergeometric function
Low- and high-frequency limits
The low-frequency limit when there is enough time for the wave-induced pore
pressures to equilibrate is referred to as the “relaxed” or “quasi-static” limit with
P-wave phase velocity V
qs
. The other limiting situation is when frequencies are high
enough that there is no time for flow-induced equilibration of pore pressures. This
limit is the “unrelaxed” or “no-flow” limit, with phase velocity V
nf
V
qs
. Though the
no-flow limit might be called the “high-frequency” limit, the wavelengths are still
much longer than the scale of the heterogeneities. The limiting velocities for the
P-wave are given by (Muller and Gurevich, 2005b)
V
qs
¼ V
0
ð1
2
Þ
V
nf
¼ V
0
ð1 þ
1
2
Þ
and the relative magnitude of the velocity dispersion effect is
V
nf
V
qs
V
0
¼
1
The limiting velocities do not depend on the spatial correlation functions and are
independent of geometry of the heterogeneities. For a porous medium, such that
all poroelastic moduli are homogeneous and the only fluctuations are in the bulk
modulus of the fluid, the quasi-static limit corresponds to a Reuss average (Wood’s
average) of the pore-fluid bulk moduli, followed by Gassmann’s fluid substitution
335 6.19 Heterogeneous poroelastic media

(see Section 6.3); the no-flow limit corresponds to a Hill’s average (Section 4.5)of
the saturated P-wave moduli.
In the low-frequency limit, Q
1
/ o, while for correlation functions that can be
expanded in a power series as
Bðr=aÞ¼1 ðr=aÞþOðr
2
=a
2
Þþ
the high-frequency asymptotic behavior of Q
1
is given by Q
1
/ 1=
ffiffiffiffi
o
p
. For
a Gaussian correlation function, there is a much faster decrease of attenuation with
frequency given by Q
1
/ 1=o. For all correlation functions, maximum attenuation
occurs at the resonance condition when the diffusion wavelength equals the correl-
ation length or k
Ps
a 1: The corresponding frequency is given as o
max
2k
0
N=a
2
.
Permeability fluctuations
The equations in the above sections for the effective P-wavenumber
k
P
in three-
dimensional random poroelastic media were derived for a medium with a homogeneous
permeability. Muller and Gurevich (2006) extended the theory to take into account
spatial fluctuations of permeability, and derive expressions for the effective slow
P-wavenumber
k
Ps
. They also identify a dynamic permeability for the heterogeneous
poroelastic medium. The dynamic permeability of Muller and Gurevich is different
from the dynamic permeability of Johnson et al. (1987), which is frequency-dependent
permeability arising from inertial effects at frequencies of the order of Biot’s charac-
teristic frequency. The dynamic permeability of Muller and Gurevich is related to
wave-induced flow at frequencies much lower than the Biot characteristic frequency.
The relative fluctuation in the property X is denoted by e
X
with zero mean and
variance
2
XX
. The fluctuation of permeability, k, is parameterized in terms of the
variance
2
pp
of the reciprocal permeability p ¼ 1=k. The slow P-wave effective
wavenumber is given as (Muller et al., 2007):
k
2
Ps
¼ k
2
Ps
1 þ
S
xðoÞ½
xðoÞ¼1 þ k
2
Ps
Z
1
0
rBðrÞexpðik
Ps
rÞdr
S
¼
a
2
M
P
d
e
a
e
K
f
þ e
2
*+
þ
2
pp
3
where
hi
denotes ensemble averages. For a one-dimensional random medium
x
ð1DÞ
ðoÞ¼1 þ ik
Ps
Z
1
0
BðrÞexpðik
Ps
rÞdr
ð1DÞ
S
¼
a
2
M
P
d
e
a
e
K
f
þ e
2
*+
þ
2
pp
336 Fluid effects on wave propagation
